湘教版九年级上册 4.4《解直角三角形的应用》【同步练习】(解析版)
文档属性
| 名称 | 湘教版九年级上册 4.4《解直角三角形的应用》【同步练习】(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 621.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-07 00:00:00 | ||
图片预览



文档简介
《解直角三角形的应用》同步练习
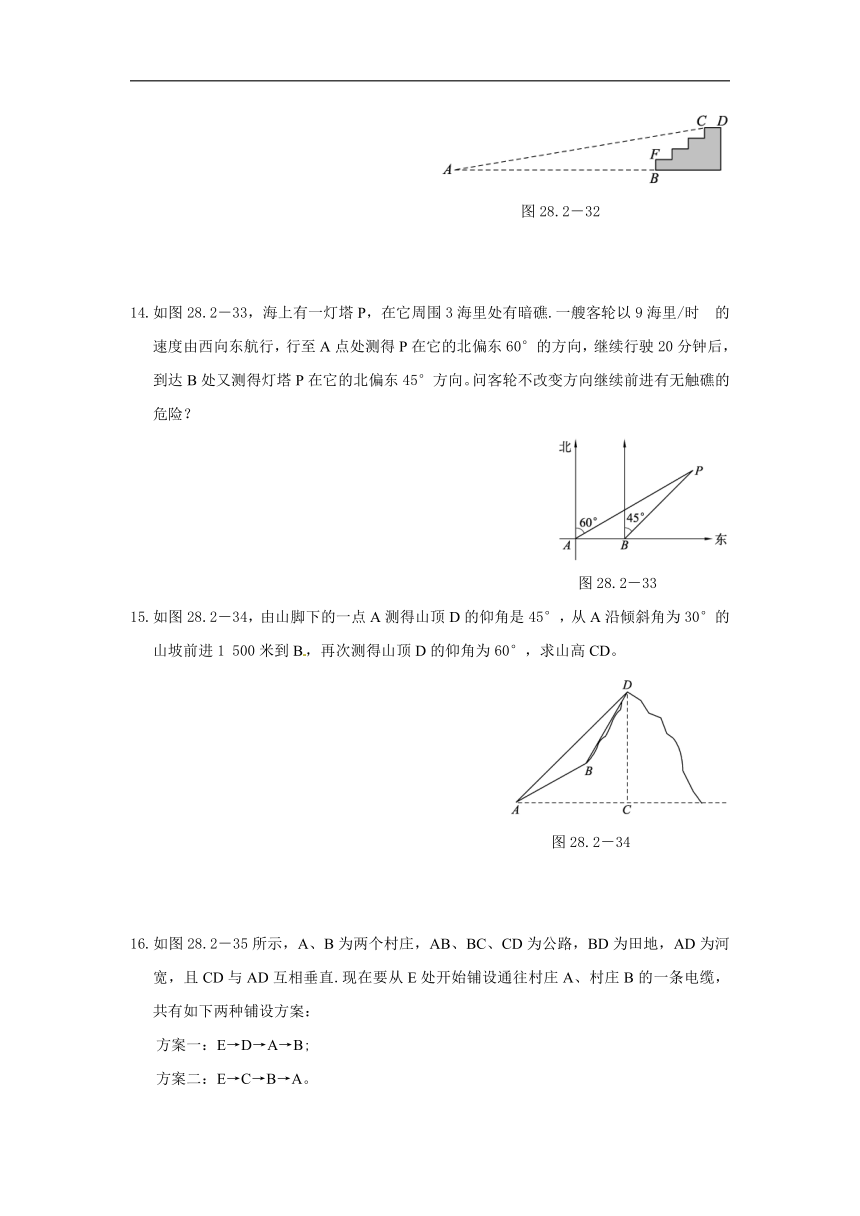
1.如图28.2-21,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为( )
A.a B.2a C. D.
图28.2-21 图28.2-22 (第3题)
2.如图28.2-22,梯形护坡石坝的斜坡AB的坡度i=1∶3,坝高BC为2米,则斜坡AB的长是( )
A.米 B.米 C.米 D.6米
3.AE、CF是锐角△ABC的两条高,如果AE∶CF=3∶2,则sinA∶sinC等于( )
A.3∶2 B.2∶3 C.9∶4 D.4∶9
4.如图28.2-29,某飞机于空中A处探测倒地面目标B,此时从飞机上看目标B的俯角α=30°,飞行高度AC=1 200米,则飞机到目标B的距离AB为( )
A.1 200米 B.2 400米 C.米 D.米
图28.2-29 图28.2-30 图28.2-31
5.一人乘雪橇沿坡比1∶的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s=10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为( )
A.72 m B.36 m C.36 m D. m
6.如图28.2-31,测量队为了测量某地区山顶P的海拔高度,选M点作为观测点,从M点测量山顶P的仰角为30°,在比例尺为1∶50 000的该地区等高线地形图上,量得这两点的图上距离为6厘米,则山顶P的海拔高度为( )
A.1 732米 B.1 982米 C.3 000米 D.3 250米
7.如图28.2-23,等腰三角形ABC的顶角为120°,腰长为10,则底边上的高AD=________。
图28.2-23 图28.2-24
8.如图28.2-24是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD=_______度(不考虑青蛙的身高)。
9.如图28.2-25,小勇想估测家门前的一棵树的高度,他站在窗户C处,观察到树顶端A正好与C处在同一水平线上,小勇测得树底B的俯角为60°,并发现B点距墙脚D之间恰好铺设有六块边长为0.5米的正方形地砖,因此测算出B点到墙脚之间的距离为3米,请你帮助小勇算出树的高度AB约多少米?(结果保留1位小数)
图28.2-25
10.如图28.2-26,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°。已知AB=20 米,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留一位小数)。
图28.2-26
11.初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图28.2-27所示,A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60°方向,C点在B点北偏东45°方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长。(结果精确到0.01米)
图28.2-27
12.如图28.2-28,城市规划期间,要拆除一电线杆AB,已知距电线杆水平距离14米的D处有一大坝,背水坡的坡度i=2∶1,坝高CF为2米,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2米的人行道.请问:在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)。
图28.2-28
13.某商场门前的台阶截面积如图28.2-32所示.已知每级台阶的席度(如CD)均为0.3 m,高度(如BE)均为0.2 m.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离(精确到0.1 m)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16)。
图28.2-32
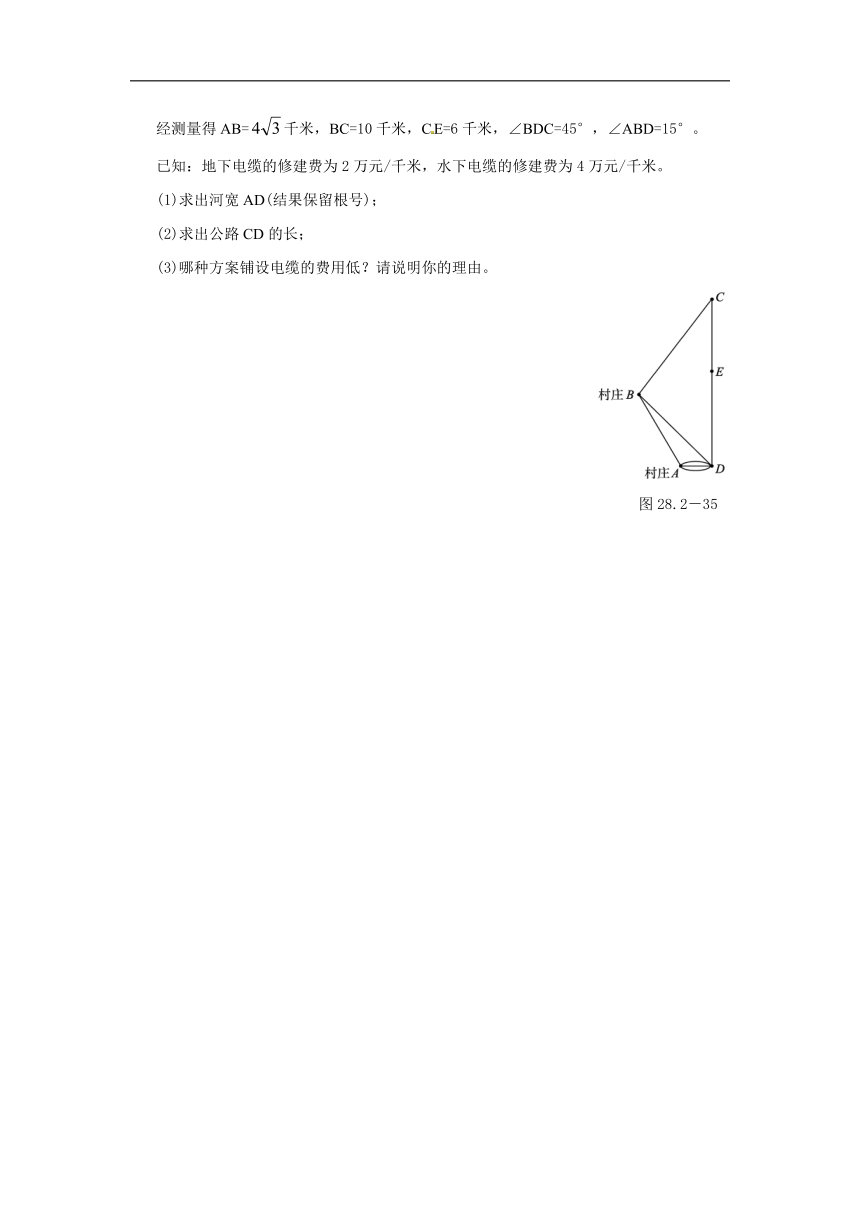
14.如图28.2-33,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时?的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向。问客轮不改变方向继续前进有无触礁的危险?
图28.2-33
15.如图28.2-34,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1 500米到B,再次测得山顶D的仰角为60°,求山高CD。
图28.2-34
16.如图28.2-35所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
方案一:E→D→A→B;
方案二:E→C→B→A。
经测量得AB=千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°。
已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米。
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由。
图28.2-35
参考答案
1.思路解析:直接用等腰直角三角形的性质。
答案:B
2.思路解析:坡度的定义,所以BC∶AC∶AB=1∶3∶。
答案:B
3.思路解析:画出图形,在Rt△AFC中,sinA=;在Rt△AEC中,sinC=。
所以sinA∶sinC==CF∶AE=2∶3。
答案:B
4.思路解析:∠ABC=α,解直角三角形。
答案:B
5.思路解析:根据公式,算出斜坡的坡长,构造斜边为s的直角三角形,用坡比的定义解答。
答案:C
6.思路解析:等高线地图上,两点的图上距离是指两点的水平距离,山顶的海拔高度是指P点的竖直高度,画出视线、两点的水平距离、高度的示意图,它们可以构成直角三角形,通过解直角三角形求出。
如图,在Rt△POM中,∠O=90°,∠M=30°,OM=6×500=3 000(米),
因为tanM=,所以OP=OM×tan30°=3 000×≈1 732(米)。
答案:A
7.答案:5
8.思路解析:在Rt△OBC中,OB=OC,可以得到∠BOC=45°,所以∠COD=2∠BOC=90°。
答案:90°
9.思路解析:在Rt△ABC中,∠A=90°,∠BCA=60°,AC=3米,用正切函数关系求出AB的长。
解:如图,在Rt△ABC中,AC=BD=3米,tan∠BCA=,
所以AB=AC×tan∠BCA=3×tan60°=3×≈5.2 (米)。
答:树的高度AB约为5.2米。
10.思路解析:作出气球离地面的高度,构成了直角三角形,利用直角三角形求解。
解:作CD⊥AB,垂足为D.设气球离地面的高度是x米。
在Rt△ACD中,∠CAD=45°,所以AD=CD=x。
在Rt△CBD中,∠CBD=60°,所以tan60°=,BD=。
因为AB=AD-BD,所以20=x-.解得x≈47.3(米)。
答:气球离地面的高度约是47.3米。
11.思路解析:作高构造直角三角形并寻找线段之间的关系。
解:过点B作BE⊥AD,BF⊥CD,垂足分别为E、F.由题意,知AD⊥CD。
因为四边形BFDE为矩形,所以BF=ED。
在Rt△ABE中,AE=AB×cos∠EAB,
在Rt△BCF中,BF=BC×cos∠FBC,
所以AD=AE+BF=20×cos60°+40×cos45°=20×+40×=10+,
即AD≈10+20×1.414=38.28(米)。
12.思路解析:有没有必要将此人行道封上,就要看电线杆倒下时,能不能到达人行道上,若AB>BE,则电线杆会倒到人行道上.只要计算出AB的长,利用30°仰角这个条件,可以在点C处作CH⊥AB,在Rt△AHC中解直角三角形。
解:在拆除电线杆AB时,不需要将此人行道封上.理由如下:
作CH⊥AB,垂足为H。
在Rt△CDF中,I=,所以DF= CF=×2=1(米)。
所以HC=BF=BD+DF=14+1=15(米)。
在Rt△AHC中,tan∠ACH=,
所以AH=HC×tan∠ACH=15×tan30°=15×≈8.7(米)。
因此AB=AH+HB=AH+CF=8.7+2=10.7(米)。
因为BE=BD-DE=14-2=12(米),10.7<12,
所以电线杆不会倒到人行道上,不需要将此人行道封上。
13.思路解析:根据图形,构造直角三角形。
解:如图,过C作CF⊥AB交AB的延长线于F。
由条件,得CF=0.8 m,BF=0.9 m。
在Rt△CAF中,∵tanA=,∴AF≈=5(m)。
∴AB=AF-BF=5-0.9=4.1(m)。
答:从斜坡起点A到台阶前点B的距离约为4.1 m。
14.思路解析:构造直角三角形,用方程求解点P到AB的距离,若这个距离大于3海里,表明客轮在暗礁范围外,客轮不会触礁。
解:过P作PC⊥AB于C点,据题意知: AB=9×=3。
∵∠PCB=90°,∠PBC=90°-45°=45°,
∴PC=BC。
在Rt△PAC中,∠PAB=90°-60°=30°,
∴tan30°=,
即.∴。
∴客轮不改变方向继续前进无触礁危险。
15.思路解析:题目中知道AB的长,需要把AB转化到直角三角形中,考虑∠DBE=60°,过点B分别向AC、DC作垂线,构成直角三角形。
解:过点B作CD、AC的垂线,垂足分别为E、F。
∵∠BAC=30°,AB=1 500米,
∴BF=EC=750米,AF=米。
设FC=x米,
∵∠DBE=60°,∴DE=米。
又∵∠DAC=45°,∴AC=CD,
即+x=750+米.得x=750。
∴CD=(750+)米。
答:山高CD为(750+)米。
16.方案一:E→D→A→B;
方案二:E→C→B→A。
经测量得AB=千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°。
已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米。
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由。
思路解析:这是一道几何应用题,解题时要善于把实际问题抽象成几何图形,并领会图形中的几何元素代表的意义,由题意可分析出,当A点距台风中心不超过160千米时,会受台风影响,若过A作AD⊥BC于D,设E,F分别表示A市受台风影响的最初、最后时台风中心的位置,则AE=AF=160千米;当台风中心位于D处时,A市受台风影响的风力最大。
解:(1)如图,经过点A作AD⊥BC,垂足为D。
在Rt△ABD中,AB=220,∠B=30°。
所以AD=110(千米)。
由题意,当A点距台风中心不超过160千米时,将会受到台风的影响.故该城市会受到这次台风的影响。
(2)由题意,当A点距台风中心不超过160千米时,将会受到台风的影响,由对称性可以知道AE=AF=160千米.当台风中心从E处移到F处时,该城市都会受到这次台风的影响。
在Rt△ADE中,由勾股定理,得
。
所以EF= (千米)。
因为该台风中心以15千米/时的速度移动。
所以这次台风影响该城市的持续时间为 (小时)。
(3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为(级)。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
