人教版八年级数学上册11.3.2 多边形的内角和课件(23张ppt)
文档属性
| 名称 | 人教版八年级数学上册11.3.2 多边形的内角和课件(23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 520.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-09 09:58:28 | ||
图片预览





文档简介
(共23张PPT)
第 十一章 三角形
第十一章 三角形
11.3.2 多边形的内角和
学 习 目 标
1
2
掌握多边形的内角和公式与外角和定理. (重点)
会用多边形的内角和公式与外角和定理进行简单的计算与说理. (难点)
新课导入
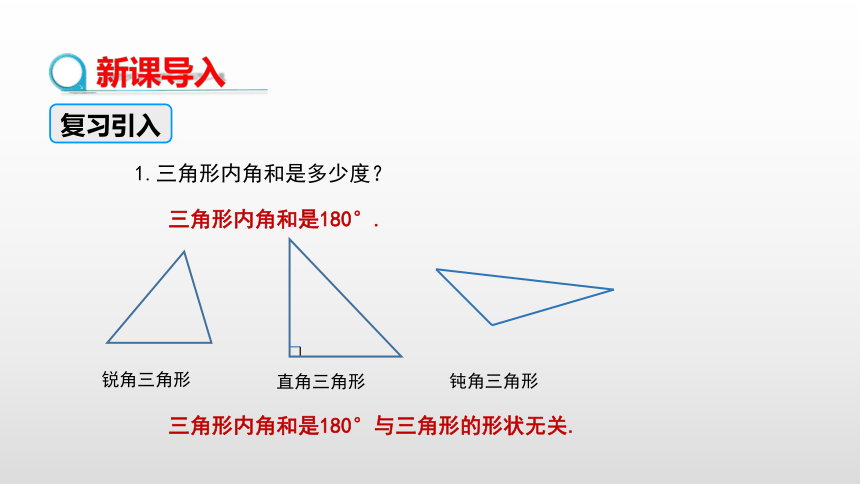
1.三角形内角和是多少度?
复习引入
三角形内角和是180°.
锐角三角形
钝角三角形
直角三角形
三角形内角和是180°与三角形的形状无关.
2.长方形和正方形的内角和是多少度?
都是360°.
思考: 1.你能猜想任意四边形的内角和是多少度吗?
2.五边形、六边形的内角和又是多少?
知识讲解
★ 多边形的内角和
猜想:任意四边形的内角和是多少度?
任意四边形的内角和都是360°.
验证:
方法1:如图,连接,则该四边形被分为两个三角形,
所以四边形内角和为180°×2=360°.
A
B
C
D
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE、DE,
则该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
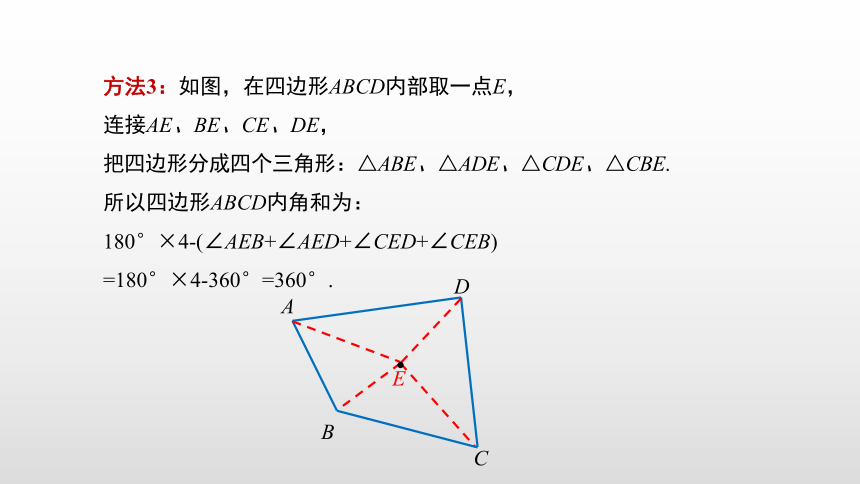
方法3:如图,在四边形ABCD内部取一点E,
连接AE、BE、CE、DE,
把四边形分成四个三角形:△ABE、△ADE、△CDE、△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
A
B
C
D
P
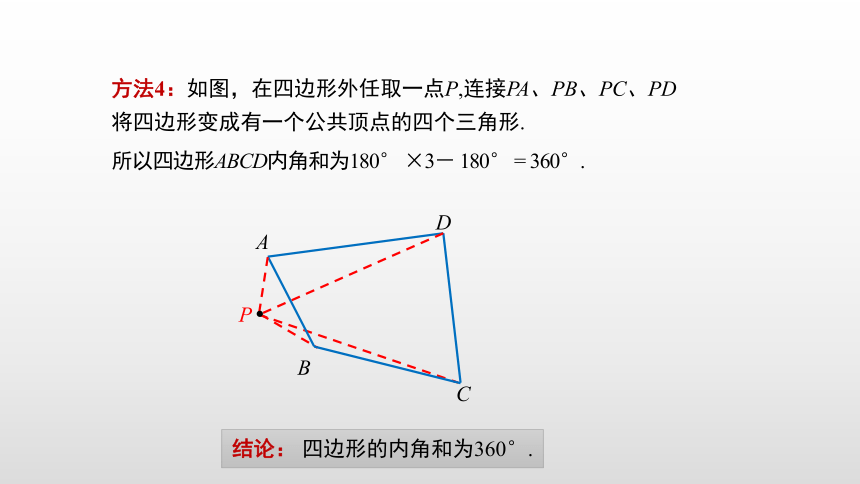
方法4:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180° ×3- 180° = 360°.
结论: 四边形的内角和为360°.
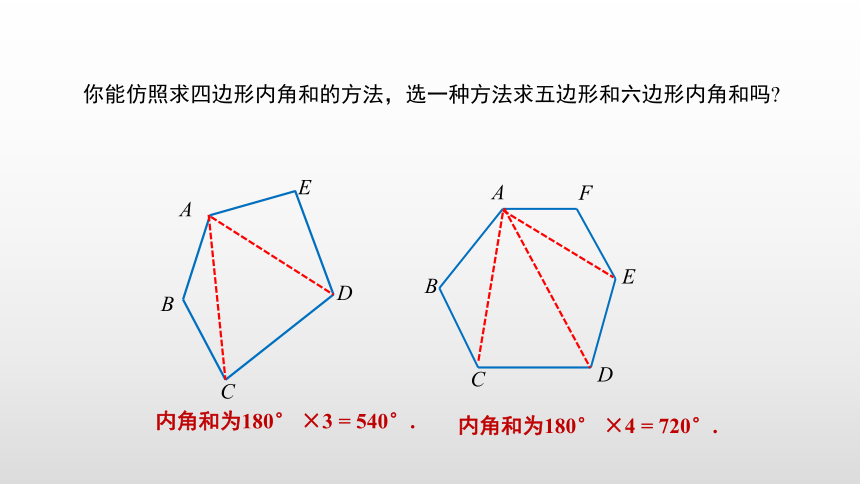
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
A
C
D
E
B
A
B
C
D
E
F
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °
例1 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)?180=360+720,
解得n=8.
∴多边形的内角和为(8-2)×180°=1080°.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为 1080°÷8=135°.
★ 多边形的外角和
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
A
B
C
D
E
F
1
3
2
4
5
6
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:六个外角加上它们分别相邻的六个内角和是多少?
互补
6×180°=1080°
问题3:这六个平角和与六边形的内角和、外角和有什么关系?
六边形外角和
=360 °.
=六个平角
-六边形内角和
=6×180°
A
B
C
D
E
F
1
3
2
4
5
6
结论:六边形的外角和等于360°.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:把六边形换成n边形( n 为不小于3的任意整数),可以得到同样的结果吗?
与边数无关
正多边形每个内角的度数是
正多边形每个外角的度数是
拓 展
例2 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360°,
∴ (n-2)?180°=2× 360?.
解得 n=6.
∴这个多边形的边数为6.
随堂训练
2.若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
C
3.如果一个多边形的内角和是外角和的3 倍,则这个多形的边数是( )
A.8 B.9 C.10 D.11
A
1.正多边形的一个内角是150 °,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
D
4.一个正多边形的内角和为720°,则这个正多边形的每一个内角等于______.
120°
5.如图所示,小华从 点出发,沿直线前进10 m 后左转24 °,再沿直线前进10 m,又向左转24°,…,照这样走下去,他第一次回到出发地A 点时,一共走的路程是______.
150 m
6.如图,四边形中,去掉一个60°的∠ 得到一个五边形,求∠1+ ∠2 的度数.
解法1 :如图所示,
∵ ∠1 =∠∠, ∴ ∠2 =∠∠,
∠ = 60°,
∴ ∠∠∠ ∠∠∠.
解法2 :∵ ∠∠∠∠,∠,
∴ ∠∠∠.
又∠∠∠∠∠,
∴ ∠1+∠2 = 540°-300°=240° .
解法3 :∵ ∠∠∠,∠,
∴ ∠∠.
∵ ∠∠1 = 180°,∠∠2 = 180°,
∴ ∠∠1+∠∠2 = 360°,
∴ ∠1+∠2 = 360°-120°= 240° .
7.如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.
∵AP平分∠EAB,∴∠PAB= ∠EAB.
同理可得∠ABP= ∠ABC.
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°.
课堂小结
多边形的内角和
内角和公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
内角= ,外角=
正多边形
第 十一章 三角形
第十一章 三角形
11.3.2 多边形的内角和
学 习 目 标
1
2
掌握多边形的内角和公式与外角和定理. (重点)
会用多边形的内角和公式与外角和定理进行简单的计算与说理. (难点)
新课导入
1.三角形内角和是多少度?
复习引入
三角形内角和是180°.
锐角三角形
钝角三角形
直角三角形
三角形内角和是180°与三角形的形状无关.
2.长方形和正方形的内角和是多少度?
都是360°.
思考: 1.你能猜想任意四边形的内角和是多少度吗?
2.五边形、六边形的内角和又是多少?
知识讲解
★ 多边形的内角和
猜想:任意四边形的内角和是多少度?
任意四边形的内角和都是360°.
验证:
方法1:如图,连接,则该四边形被分为两个三角形,
所以四边形内角和为180°×2=360°.
A
B
C
D
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE、DE,
则该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
方法3:如图,在四边形ABCD内部取一点E,
连接AE、BE、CE、DE,
把四边形分成四个三角形:△ABE、△ADE、△CDE、△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
A
B
C
D
P
方法4:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180° ×3- 180° = 360°.
结论: 四边形的内角和为360°.
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
A
C
D
E
B
A
B
C
D
E
F
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °
例1 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)?180=360+720,
解得n=8.
∴多边形的内角和为(8-2)×180°=1080°.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为 1080°÷8=135°.
★ 多边形的外角和
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
A
B
C
D
E
F
1
3
2
4
5
6
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:六个外角加上它们分别相邻的六个内角和是多少?
互补
6×180°=1080°
问题3:这六个平角和与六边形的内角和、外角和有什么关系?
六边形外角和
=360 °.
=六个平角
-六边形内角和
=6×180°
A
B
C
D
E
F
1
3
2
4
5
6
结论:六边形的外角和等于360°.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:把六边形换成n边形( n 为不小于3的任意整数),可以得到同样的结果吗?
与边数无关
正多边形每个内角的度数是
正多边形每个外角的度数是
拓 展
例2 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360°,
∴ (n-2)?180°=2× 360?.
解得 n=6.
∴这个多边形的边数为6.
随堂训练
2.若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
C
3.如果一个多边形的内角和是外角和的3 倍,则这个多形的边数是( )
A.8 B.9 C.10 D.11
A
1.正多边形的一个内角是150 °,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
D
4.一个正多边形的内角和为720°,则这个正多边形的每一个内角等于______.
120°
5.如图所示,小华从 点出发,沿直线前进10 m 后左转24 °,再沿直线前进10 m,又向左转24°,…,照这样走下去,他第一次回到出发地A 点时,一共走的路程是______.
150 m
6.如图,四边形中,去掉一个60°的∠ 得到一个五边形,求∠1+ ∠2 的度数.
解法1 :如图所示,
∵ ∠1 =∠∠, ∴ ∠2 =∠∠,
∠ = 60°,
∴ ∠∠∠ ∠∠∠.
解法2 :∵ ∠∠∠∠,∠,
∴ ∠∠∠.
又∠∠∠∠∠,
∴ ∠1+∠2 = 540°-300°=240° .
解法3 :∵ ∠∠∠,∠,
∴ ∠∠.
∵ ∠∠1 = 180°,∠∠2 = 180°,
∴ ∠∠1+∠∠2 = 360°,
∴ ∠1+∠2 = 360°-120°= 240° .
7.如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.
∵AP平分∠EAB,∴∠PAB= ∠EAB.
同理可得∠ABP= ∠ABC.
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA
=180°? (∠EAB+∠ABC)=180°? ×230°=65°.
课堂小结
多边形的内角和
内角和公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
内角= ,外角=
正多边形
