北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第19讲 轴对称含答案
文档属性
| 名称 | 北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第19讲 轴对称含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-08 00:00:00 | ||
图片预览


文档简介
轴对称
【学习目标】
1.认识和欣赏身边的轴对称图形,增进学习数学的兴趣.
2.了解轴对称以及轴对称图形的概念,弄清它们之间的区别与联系,能识别轴对称图形.
2.探索轴对称的基本性质,会画一些简单的关于某直线对称的图形.
【要点梳理】
要点一、轴对称图形 轴对称图形的定义
一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称图形,该直线就是它的对称轴.
要点诠释: 轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的对称轴不一定只有一条,也可能有两条或多条,因图形而定. 要点二、轴对称 1.轴对称定义
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点. 要点诠释: 轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对称的两个图形一定全等.
2.轴对称与轴对称图形的区别与联系
轴对称与轴对称图形的区别主要是:轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
要点三、轴对称与轴对称图形的性质
轴对称、轴对称图形的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等. 要点诠释:(1)若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【典型例题】
类型一、判断轴对称图形
1、(2019?邵阳)下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
【思路点拨】我们将图中的图形分别沿着某条直线对折,看看图形的两边能否重合,若重合则是轴对称图形,否则就不是.
【答案】D;
【解析】轴对称图形即能找到对称轴,使对称轴两边的图形重合.
【总结升华】找对称轴要注意从不同的角度去观察,做到不重复、不遗漏.
举一反三:
【变式1】下列图形中,对称轴最少的对称图形是 ( )
【答案】A;
提示:A一条对称轴,B四条对称轴,C五条对称轴,D三条对称轴.
【变式2】在直线、角、线段、等边三角形四个图形中,对称轴最多的是 ,它有 条对称轴;最少的是 ,它有 条对称轴
【答案】直线、无数、角、1.
2、观察图形…并判断照此规律从左到右第四个图形是( )
A . B. C . D.
【思路点拨】根据题意分析图形涂黑规律,求得结果,采用排除法判定正确选项.
【答案】D;
【总结升华】本题考查学生根据图形,归纳、发现并运用规律的能力.注意结合图形解题的思想.
举一反三:
【变式】将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A. B. C. D.
【答案】C.
类型二、轴对称或轴对称图形的应用
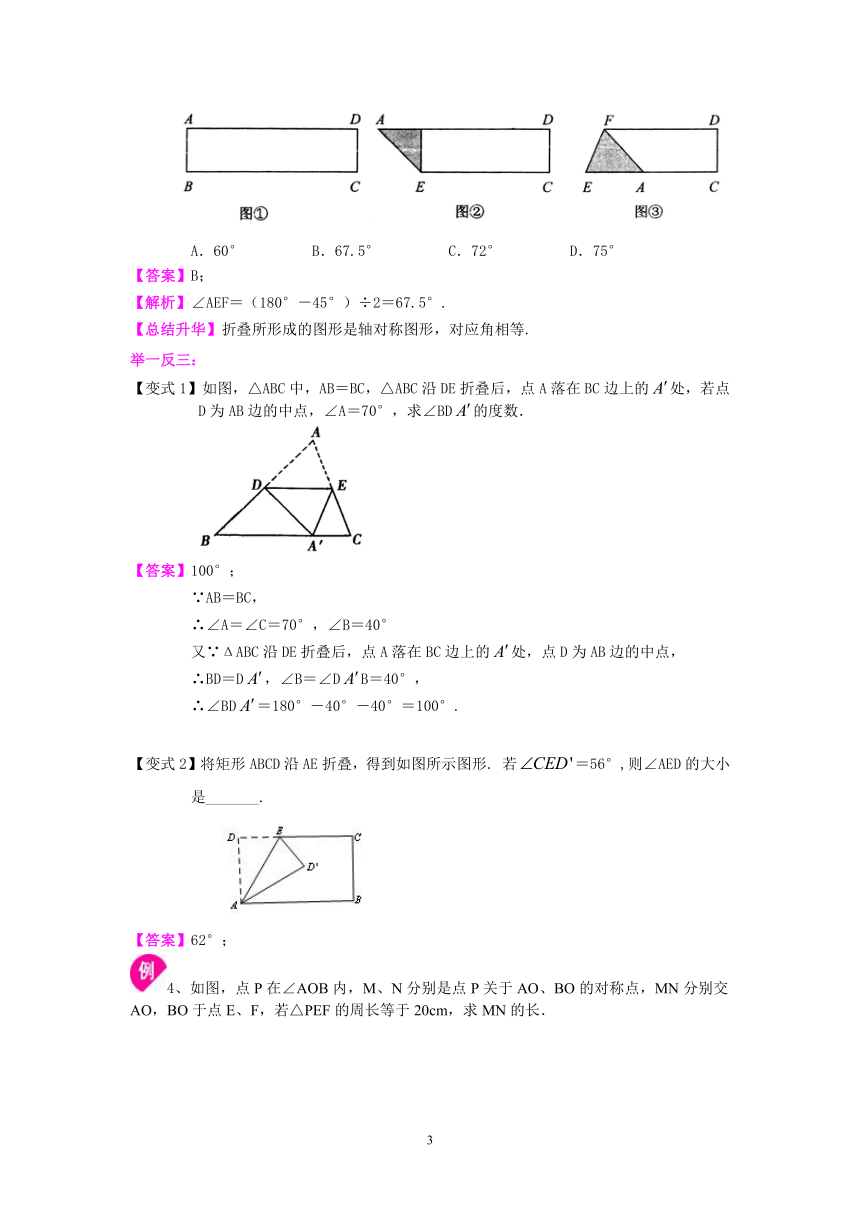
3、如图,将矩形纸片ABCD (图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E (如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F (如图③); (3)将纸片收展平,那么∠AEF的度数为( )
A.60° B.67.5° C.72° D.75°
【答案】B;
【解析】∠AEF=(180°-45°)÷2=67.5°.
【总结升华】折叠所形成的图形是轴对称图形,对应角相等.
举一反三:
【变式1】如图,△ABC中,AB=BC,△ABC沿DE折叠后,点A落在BC边上的处,若点D为AB边的中点,∠A=70°,求∠BD的度数.
【答案】100°;
∵AB=BC,
∴∠A=∠C=70°,∠B=40°
又∵ΔABC沿DE折叠后,点A落在BC边上的处,点D为AB边的中点,
∴BD=D,∠B=∠DB=40°,
∴∠BD=180°-40°-40°=100°.
【变式2】将矩形ABCD沿AE折叠,得到如图所示图形. 若=56°,则∠AED的大小是_______.
【答案】62°;
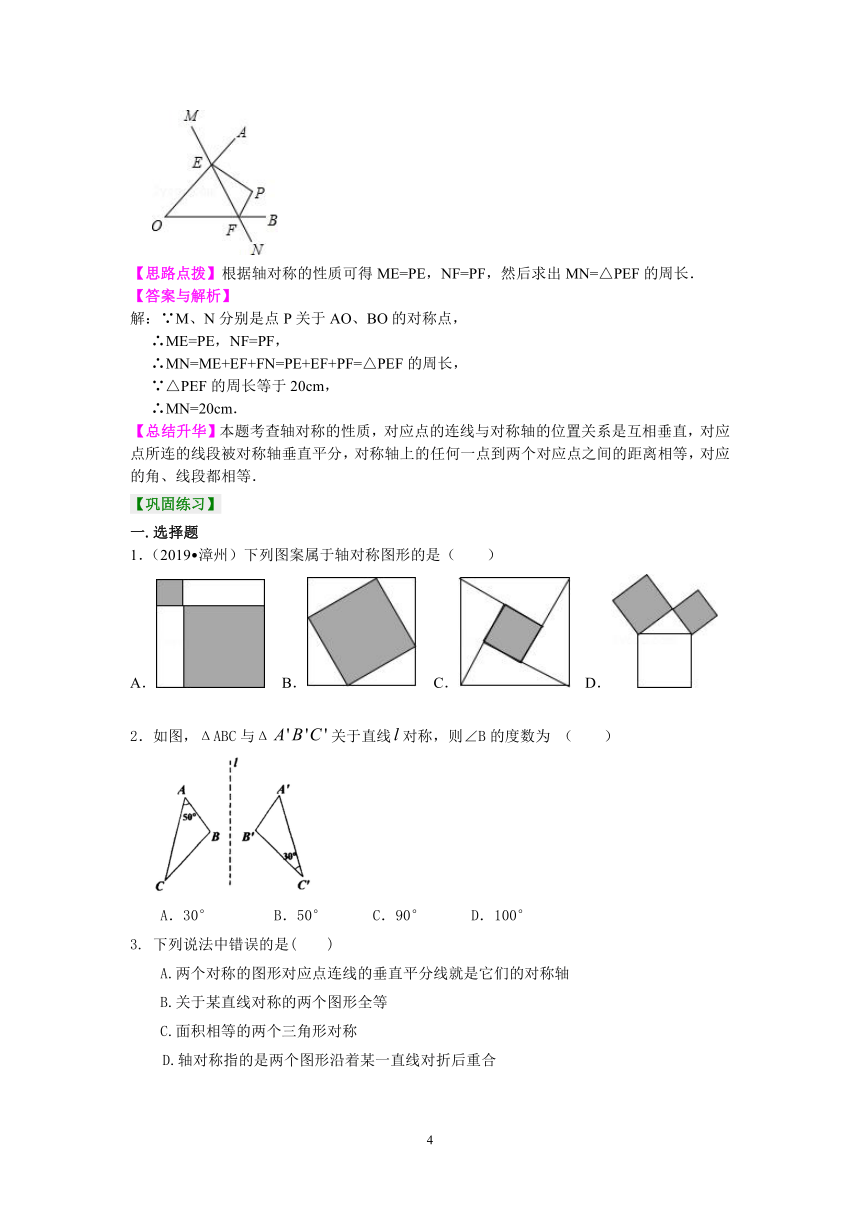
4、如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
【思路点拨】根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长.
【答案与解析】
解:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
【总结升华】本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
【巩固练习】
一.选择题
1.(2019?漳州)下列图案属于轴对称图形的是( )
A. B. C. D.
2.如图,ΔABC与Δ关于直线对称,则∠B的度数为 ( )
A.30° B.50° C.90° D.100°
3. 下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个三角形对称
D.轴对称指的是两个图形沿着某一直线对折后重合
4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( )
A.(3,1) B.(﹣3,﹣1) C.(1,﹣3) D.(3,﹣1)
5. 下列说法错误的是( )
A. 若A,A′是以BC为轴对称的点,则AA′垂直平分BC
B. 线段的一条对称轴是它本身所在的直线
C. 一条线段的一个端点的对称点是另一个端点
D. 等边三角形是轴对称图形
6.将如图①的矩形ABCD纸片沿EF折叠得到图②,折叠后DE与BF相交于点P,如果∠BPE=130°,则∠PEF的度数为( )
A.60° B.65° C.70° D.75°
二.填空题
7. (2019?赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号)
8.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有 个.
9. 如图,等边△ABC的边长为2,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点处,且点在△ABC外部,则阴影部分图形的周长为 .
10.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
11. 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD : ∠DBA =3:1,则∠A的度数为________.
12.利用折纸的方法,将1条线段分成16段彼此相等的线段,需要折 次.
三.解答题
13. 如图所示,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?
14.如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,
(1)求线段MN的长,
(2)若∠AOB=30°,求OM的长.
15.如图,在4×3正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】根据轴对称图形的定义判断.
2. 【答案】D;
【解析】成轴对称的两个图形对应线段、对应角相等.
3. 【答案】C;
【解析】面积相等不一定全等,也不一定对称.
4. 【答案】A;
【解析】解:由A点坐标,得C(﹣3,1).
由翻折得C′与C关于y轴对称,C′(3,1).
故选:A.
5. 【答案】A;
【解析】A、应该是BC垂直平分AA′,故本选项错误;B、线段的一条对称轴是它本身所在的直线,故本选项正确;C、一条线段的一个端点的对称点是另一个端点,故本选项正确;D、等边三角形是轴对称图形,故本选项正确.
6. 【答案】B;
【解析】解:∵AE∥BF,
∴∠AEP=180°﹣∠BPE=180°﹣130°=50°.
又∵折叠后DE与BF相交于点P,设∠PEF=x,
即∠AEP+2∠PEF=180°,
即50°+2x=180°,
x=65°.
故选:B.
二.填空题
7.【答案】①②③④ .
8. 【答案】3;
【解析】解:如图所示,有3个使之成为轴对称图形.
故答案为:3.
9. 【答案】6;
【解析】根据对称性,阴影部分的周长等于△ABC的周长=6.
10.【答案】70;
【解析】∵CD与BE互相垂直平分,∴DB=DE,∵∠BDE=70°,∴∠BDC=35°,∠ABD=55°,∵AD⊥DB,∴∠BAD=90°-55°=35°,根据轴对称性,四边形ACBD关于直线AB成轴对称,∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
11.【答案】18°;
【解析】∠A=∠ABD=,∠CBD=3,5=90°,=18°.
12.【答案】4;
【解析】因为24=16,所以需折4次.
三.解答题
13.【解析】
在实际中的算式是:151+25+12=188;结果也是正确的.
14.【解析】
解:(1)根据题意,EP=EM,PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm.
(2)连接OM、OP、ON,
∵M、N分别是点P关于直线OA、OB的对称点,
∴∠MOA=∠POA,∠NOB=∠POB,
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴OM=ON=MN=20cm.
15.【解析】
解:如图所示,答案不唯一,参见下图.
【学习目标】
1.认识和欣赏身边的轴对称图形,增进学习数学的兴趣.
2.了解轴对称以及轴对称图形的概念,弄清它们之间的区别与联系,能识别轴对称图形.
2.探索轴对称的基本性质,会画一些简单的关于某直线对称的图形.
【要点梳理】
要点一、轴对称图形 轴对称图形的定义
一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称图形,该直线就是它的对称轴.
要点诠释: 轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的对称轴不一定只有一条,也可能有两条或多条,因图形而定. 要点二、轴对称 1.轴对称定义
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点. 要点诠释: 轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对称的两个图形一定全等.
2.轴对称与轴对称图形的区别与联系
轴对称与轴对称图形的区别主要是:轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
要点三、轴对称与轴对称图形的性质
轴对称、轴对称图形的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等. 要点诠释:(1)若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【典型例题】
类型一、判断轴对称图形
1、(2019?邵阳)下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
【思路点拨】我们将图中的图形分别沿着某条直线对折,看看图形的两边能否重合,若重合则是轴对称图形,否则就不是.
【答案】D;
【解析】轴对称图形即能找到对称轴,使对称轴两边的图形重合.
【总结升华】找对称轴要注意从不同的角度去观察,做到不重复、不遗漏.
举一反三:
【变式1】下列图形中,对称轴最少的对称图形是 ( )
【答案】A;
提示:A一条对称轴,B四条对称轴,C五条对称轴,D三条对称轴.
【变式2】在直线、角、线段、等边三角形四个图形中,对称轴最多的是 ,它有 条对称轴;最少的是 ,它有 条对称轴
【答案】直线、无数、角、1.
2、观察图形…并判断照此规律从左到右第四个图形是( )
A . B. C . D.
【思路点拨】根据题意分析图形涂黑规律,求得结果,采用排除法判定正确选项.
【答案】D;
【总结升华】本题考查学生根据图形,归纳、发现并运用规律的能力.注意结合图形解题的思想.
举一反三:
【变式】将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A. B. C. D.
【答案】C.
类型二、轴对称或轴对称图形的应用
3、如图,将矩形纸片ABCD (图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E (如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F (如图③); (3)将纸片收展平,那么∠AEF的度数为( )
A.60° B.67.5° C.72° D.75°
【答案】B;
【解析】∠AEF=(180°-45°)÷2=67.5°.
【总结升华】折叠所形成的图形是轴对称图形,对应角相等.
举一反三:
【变式1】如图,△ABC中,AB=BC,△ABC沿DE折叠后,点A落在BC边上的处,若点D为AB边的中点,∠A=70°,求∠BD的度数.
【答案】100°;
∵AB=BC,
∴∠A=∠C=70°,∠B=40°
又∵ΔABC沿DE折叠后,点A落在BC边上的处,点D为AB边的中点,
∴BD=D,∠B=∠DB=40°,
∴∠BD=180°-40°-40°=100°.
【变式2】将矩形ABCD沿AE折叠,得到如图所示图形. 若=56°,则∠AED的大小是_______.
【答案】62°;
4、如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
【思路点拨】根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长.
【答案与解析】
解:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
【总结升华】本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
【巩固练习】
一.选择题
1.(2019?漳州)下列图案属于轴对称图形的是( )
A. B. C. D.
2.如图,ΔABC与Δ关于直线对称,则∠B的度数为 ( )
A.30° B.50° C.90° D.100°
3. 下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个三角形对称
D.轴对称指的是两个图形沿着某一直线对折后重合
4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( )
A.(3,1) B.(﹣3,﹣1) C.(1,﹣3) D.(3,﹣1)
5. 下列说法错误的是( )
A. 若A,A′是以BC为轴对称的点,则AA′垂直平分BC
B. 线段的一条对称轴是它本身所在的直线
C. 一条线段的一个端点的对称点是另一个端点
D. 等边三角形是轴对称图形
6.将如图①的矩形ABCD纸片沿EF折叠得到图②,折叠后DE与BF相交于点P,如果∠BPE=130°,则∠PEF的度数为( )
A.60° B.65° C.70° D.75°
二.填空题
7. (2019?赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号)
8.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有 个.
9. 如图,等边△ABC的边长为2,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点处,且点在△ABC外部,则阴影部分图形的周长为 .
10.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
11. 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD : ∠DBA =3:1,则∠A的度数为________.
12.利用折纸的方法,将1条线段分成16段彼此相等的线段,需要折 次.
三.解答题
13. 如图所示,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?
14.如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,
(1)求线段MN的长,
(2)若∠AOB=30°,求OM的长.
15.如图,在4×3正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】根据轴对称图形的定义判断.
2. 【答案】D;
【解析】成轴对称的两个图形对应线段、对应角相等.
3. 【答案】C;
【解析】面积相等不一定全等,也不一定对称.
4. 【答案】A;
【解析】解:由A点坐标,得C(﹣3,1).
由翻折得C′与C关于y轴对称,C′(3,1).
故选:A.
5. 【答案】A;
【解析】A、应该是BC垂直平分AA′,故本选项错误;B、线段的一条对称轴是它本身所在的直线,故本选项正确;C、一条线段的一个端点的对称点是另一个端点,故本选项正确;D、等边三角形是轴对称图形,故本选项正确.
6. 【答案】B;
【解析】解:∵AE∥BF,
∴∠AEP=180°﹣∠BPE=180°﹣130°=50°.
又∵折叠后DE与BF相交于点P,设∠PEF=x,
即∠AEP+2∠PEF=180°,
即50°+2x=180°,
x=65°.
故选:B.
二.填空题
7.【答案】①②③④ .
8. 【答案】3;
【解析】解:如图所示,有3个使之成为轴对称图形.
故答案为:3.
9. 【答案】6;
【解析】根据对称性,阴影部分的周长等于△ABC的周长=6.
10.【答案】70;
【解析】∵CD与BE互相垂直平分,∴DB=DE,∵∠BDE=70°,∴∠BDC=35°,∠ABD=55°,∵AD⊥DB,∴∠BAD=90°-55°=35°,根据轴对称性,四边形ACBD关于直线AB成轴对称,∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
11.【答案】18°;
【解析】∠A=∠ABD=,∠CBD=3,5=90°,=18°.
12.【答案】4;
【解析】因为24=16,所以需折4次.
三.解答题
13.【解析】
在实际中的算式是:151+25+12=188;结果也是正确的.
14.【解析】
解:(1)根据题意,EP=EM,PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm.
(2)连接OM、OP、ON,
∵M、N分别是点P关于直线OA、OB的对称点,
∴∠MOA=∠POA,∠NOB=∠POB,
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴OM=ON=MN=20cm.
15.【解析】
解:如图所示,答案不唯一,参见下图.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
