人教版九年级数学下册第二十六章 反比例函数26.1.2反比例函数的图象和性质课件(73张PPT)
文档属性
| 名称 | 人教版九年级数学下册第二十六章 反比例函数26.1.2反比例函数的图象和性质课件(73张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-08 19:36:28 | ||
图片预览







文档简介
课件73张PPT。26.1 反比例函数人教版 数学 九年级 下册26.1.2 反比例函数的图象和性质 初步认识反比例函数的图象和性质返回(2)试一试,你能在坐标系中画出这个函数的图象吗? 刘翔在2004 年雅典奥运会110 m 栏比赛中以 12.91s 的成绩夺得金牌,被称为中国“飞人” .如果刘翔在比赛中跑完全程所用的时间为 t s,平均速度为v m/s .(1)你能写出用t 表示v 的函数
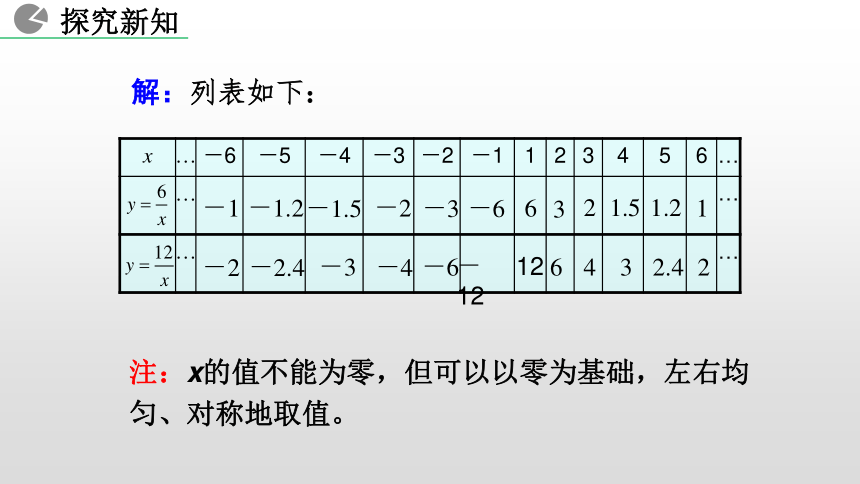
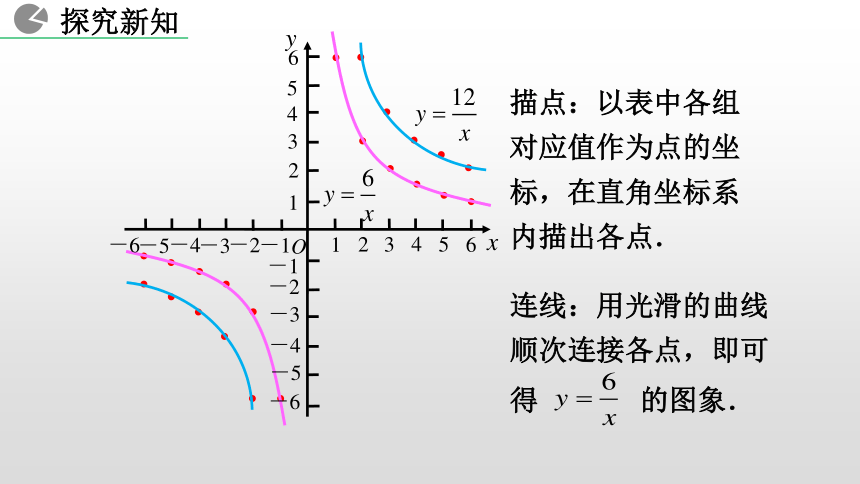
表达式吗? 2. 结合图象分析并掌握反比例函数的性质.1. 会用描点法画反比例函数的图象 .素养目标3. 体会函数的三种表示方法,领会数形结合的思想方法. 画出反比例函数 与 的图象.反比例函数的图象和性质【想一想】 用“描点法”画函数图象都有哪几步?列表描点连线解:列表如下:-1-1.2-1.5-2-3-66321.51.21-2-2.4-3-4-66432.42- 1212注:x的值不能为零,但可以以零为基础,左右均匀、对称地取值。O-2描点:以表中各组对应值作为点的坐标,在直角坐标系内描出各点.56xy4321123456-3-4-1-5-6-1-2-3-4-5-6连线:用光滑的曲线顺次连接各点,即可
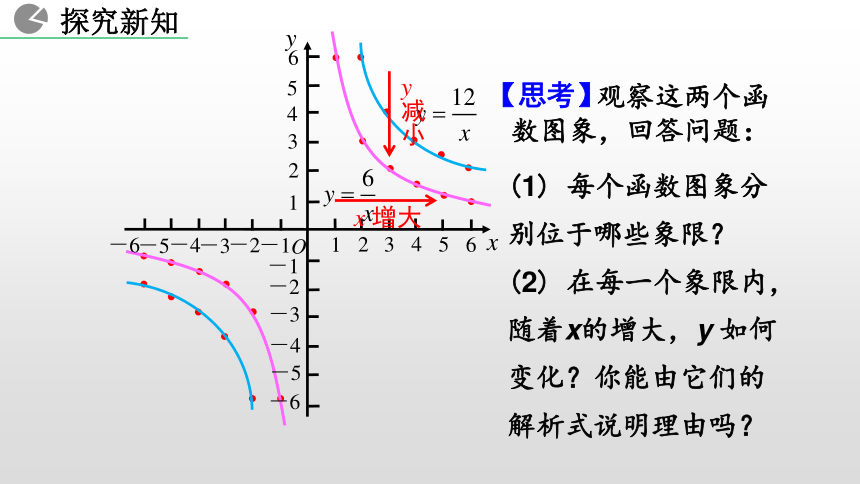
得 的图象.x 增大O-256xy4321123456-3-4-1-5-6-1-2-3-4-5-6 观察这两个函数图象,回答问题:【思考】(1) 每个函数图象分
别位于哪些象限?
(2) 在每一个象限内,
随着x的增大,y 如何
变化?你能由它们的
解析式说明理由吗?
y
减
小(3) 对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
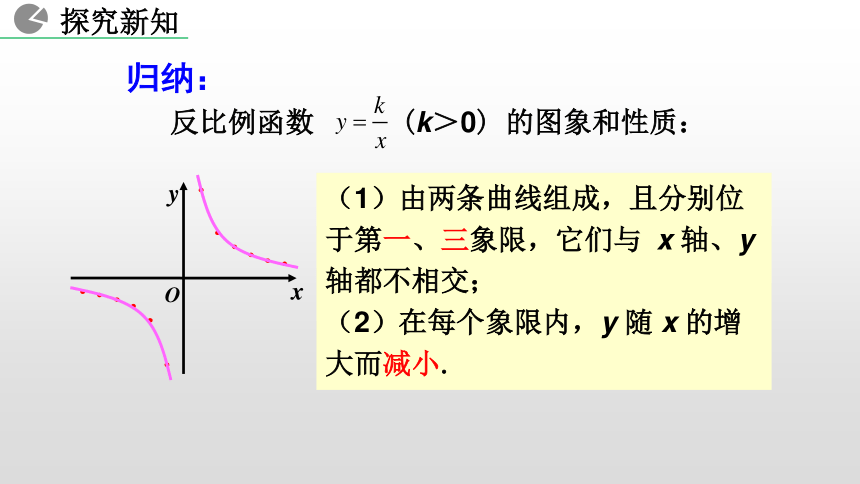
(1)由两条曲线组成,且分别位于第一、三象限,它们与 x 轴、y 轴都不相交;
(2)在每个象限内,y 随 x 的增大而减小.反比例函数 (k>0) 的图象和性质:归纳:1. (1)函数 图象在第_______象限,在每个象限内, y随x的增大而 ______. 一、三减小(2)已知反比例函数 在每一个象限内,y随x的增大而减小,则m的取值范围是_____. m>2C 例1 反比例函数 的图象上有两点 A(x1,y1),B(x2, y2),且点A,B 均在该函数图象的第一象限部分,若 x1> x2,则 y1与y2的大小关系为 ( ) 解析:因为8>0,且 A,B 两点均在该函数图象的第一象限部分,根据 x1>x2,可知y1,y2的大小关系.利用反比例函数的性质比较大小观
察
与
思
考 当 k =-2,-4,-6时,反比例函数 的图象,有哪些共同特征? 回顾上面我们利用函数图象,从特殊到一般研究反比例函数 (k>0) 的性质的过程,你能用类似的方法研究反比例函数 (k<0)的图象和性质吗? 反比例函数 (k<0) 的图象和性质:(1)由两条曲线组成,且分别位于第二、四象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而增大.归纳: 反比例函数的图象和性质形状位置增减性图象的发展趋势对称性由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一、三象限内;
当k<0时,两支双曲线分别位于第二、四象限内;当k>0时,在每一象限内, y随x的增大而减小;
当k<0时,在每一象限内, y随x的增大而增大.反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴.(1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数 与 的图象关于x轴对称,也关于y轴对称.2.(1)已知点 A(-3,a),B(-2,b),在双曲线 ,则 a___b(填>、=或<).
>(2)已知点(-1,y1),(2,y2),(3,y3)在反比例函数 (k≠0) 的图象上,则下列结论中正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y1>y2 D.y2>y3>y1B 例2 已知反比例函数 ,在每一象限内,y 随 x 的增大而增大,求a的值.解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.利用反比例函数的图象和性质求字母的值3. 已知反比例函数 在每个象限内,y 随着 x 的增大而减小,求 m 的值.解:由题意得 m2-10=-1,且 3m-8>0.
解得m=3.1.(2018?怀化)函数y=kx﹣3与 (k≠0)在同一坐标系内
的图象可能是( )
A. B. C. D.巩固练习B连接中考2.(2018?德州)给出下列函数:①y=﹣3x+2;② ;③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是( )
A.①③ B.③④ C.②④ D.②③B1.(2018?香坊区)对于反比例函数 ,下列说法
不正确的是( )
A.点(﹣2,﹣1)在它的图象上
B.它的图象在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小C2.(2018?上海)已知反比例函数 (k是常数,k≠1) 的图象有一支在第二象限,那么k的取值范围是________. 3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).(1)k<1(3)y3 >y1>y22. 已知反比例函数 y = mxm2-5,它的两个分支分别在第一、第三象限,求 m 的值.解:因为反比例函数 y = mxm2-5 的两个分支分别在第一、第三象限, 所以有解得 m=2. 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0) 的图象上,若y1<y2,求a的取值范围. 解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
∴a-1>a+1,无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1. ① 当这两点在图象的同一支上时,∵y1<y2,k>0,一、三象限双曲线k﹤0,二、四象限当k>0时,在每一象限
内, y随x的增大而减小当k﹤0时,在每一象限
内, y随x的增大而增大增减性双曲线的两支无限靠近坐标轴,但无交点对称性既是轴对称图形也是中心对称图形???
与 的图象关于x轴对称,也关于y轴对称或或反比例函数的图象和性质
的综合运用返回二、四象限一、三象限位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线 y随x的增大而增大一、三象限在每个象限, y随x的增大而减小二、四象限 y随x的增大而减小在每个象限, y随x的增大而增大
正比例函数和反比例函数的区别用对比的方法去记忆效果如何?3. 深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的思想方法.
1. 理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算中.
2.能解决反比例函数与一次函数的综合问题.素养目标 已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限? y随x的增大如何变化?
(2)点B(3,4)、C( )和D(2,5)是否在这个
函数的图象上?利用待定系数法确定反比例函数解析式
解:(1)因为点A(2,6)在第一象限,所以这个函数的图象在第一、第三象限,在每个象限内,y随x的增大而减小。解:(2)设这个反比例函数的解析式为 ,
因为点A (2,6)在其图象上,所以有 ,
解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
所以反比例函数的解析式为 .方法总结:已知反比例函数图象上一点,可以根据坐标确定点所在的象限,然后确定反比例函数的性质.或用待定系数法求出反比例函数的解析式,再判断图象性质;要判断所给的点是否在该图象上,可以将其坐标代入求得的反比例函数解析式中,若满足左边=右边,则在;若不满足左边=右边,则不在. 【讨论】已知反比例函数图象上的一点,如何确定其图象的性质?以及所给的点是否在该图象上? 1.已知反比例函数 的图象经过点 A (2,3).
(1) 求这个函数的表达式; 解:∵ 反比例函数 的图象经过点 A(2,3),
∴ 把点 A 的坐标代入表达式,得 ,
解得 k = 6.
∴ 这个函数的表达式为 .
(2) 判断点 B (-1,6),C(3,2) 是否在这个函数的图象上,并说明理由;
解:分别把点 B,C 的坐标代入反比例函数的解析式,因为点 B 的坐标不满足该解析式,点C的坐标满足该解析式,所以点 B 不在该函数的图象上,点C 在该函数的图象上. (3) 当 -3< x <-1 时,求 y 的取值范围. 解:∵ 当 x = -3时,y =-2;
当 x = -1时,y =-6,且 k > 0,
∴ 当 x < 0 时,y 随 x 的增大而减小,
∴ 当 -3 < x < -1 时,-6 < y < -2.解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图象的一支在第一象限,则另一支必在第三象限.∵函数的图象在第一、第三象限,∴ m-5>0,解得 m>5. (2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时,b<b′.【思考】根据反比例函数的部分图象,如何确定其完整图象的位置以及比例系数的取值范围?注:由于双曲线的两个分支在两个不同的象限内,因此函数y随x的增减性就不能连续的看,一定要强调“在每一象限内”,否则,笼统说k<0时,y随x的增大而增大,从而出现错误. 2. 如图,是反比例函数 的图象的一个分支,对于
给出的下列说法:
①常数k的取值范围是 ;
②另一个分支在第三象限;
③在函数图象上取点 和 ,
当 时, ;
④在函数图象的某一个分支上取点 和 ,
当 时, .
其中正确的是____________(在横线上填出正确的序号). ① ② ④ 在反比例函数 的图象上分别取点P,Q 向 x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,填写下页表格:
反比例函数中k的几何意义
5PS1 S2 4 4S1=S2S1=S2=k-5-4-3-21432-3-2-4-5-1Q 若在反比例函数 中也用同样的方法分别取 P,Q 两点,填写表格:4 4S1=S2S1=S2=-kS1 S2由前面的探究过程,可以猜想: 若点P是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,矩形AOBP 的面积与k的关系是S矩形 AOBP=|k|.S我们就 k < 0 的情况给出证明:设点 P 的坐标为 (a,b)AB∵点 P (a,b) 在函数 的图
象上,∴ ,即 ab=k.∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;若点 P 在第二象限,则 a<0,b>0,若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP=PB·PA=a· (-b)=-ab=-k.综上,S矩形 AOBP=|k|.自己尝试证明
k > 0的情况. 点 Q 是其图象上的任意一点,作 QA 垂直于 y 轴,作 QB 垂直于x 轴,矩形AOBQ 的面积与 k 的关系是 S矩形AOBQ= .
推理:△QAO与△QBO的面积和 k 的关系是
.Q对于反比例函数 ,AB|k|反比例函数的面积不变性
要
点
归
纳3.如图,点B在反比例函数 (x>0)的图象上,横坐标是1,过点B分别向x轴、y轴作垂线,垂足为A、C,则矩形OABC的面积为( )
A.1 B.2
C.3 D.4
B例1 如图,点A在反比例函数 的图象上,AC垂直 x 轴于点C,且 △AOC 的面积为2,求该反比例函数的表达式.解:设点 A 的坐标为(xA,yA),
∵点A在反比例函数
的图象上,∴ xA·yA=k,
∴反比例函数的表达式为通过图形面积确定k的值∴,∴ k=4,4.如图所示,过反比例函数 (x>0)的图象上一点A,作AB⊥x轴于点B,连接AO.若S△AOB=3,则k的值为( )
A.4 B.5
C.6 D.7
C例2 如图,P,C是函数 (x>0)图象上的任意两点,PA,CD 垂直于x 轴. 设△POA 的面积为S1,则 S1 = ;梯形CEAD 的面积为 S2,则 S1
与 S2 的大小关系是 S1 S2;
△POE 的面积 S3 和 S2 的大小
关系是S2 S3.2S1S2>=S3利用k的性质判断图形面积的关系A. SA >SB>SC B. SAC. SA =SB=SC D. SA 5. 如图,在函数 (x>0)的图象上有三点A,B ,C,过这三点分别向 x 轴、y 轴作垂线,过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为SA ,SB,SC,则 ( )CyDBACx 例3 如图,点 A 是反比例函数 (x>0)的图象上任意一点,AB//x 轴交反比例函数 (x<0) 的图象于点 B,以 AB 为边作平行四边形 ABCD,其中点 C,D 在 x 轴上,则
S四边形ABCD =___.
325?根据k的几何意义求图形的面积方法总结:解决反比例函数有关的面积问题,可以把原图形通过切割、平移等变换,转化为较容易求面积的图形.6. 如图,函数 y=-x 与函数 的图象相交于A,B 两点,过点 A,B 分别作 y 轴的垂线,垂足分别为C,D,则
四边形ACBD的面积为 ( )
A. 2 B. 4
C. 6 D. 8DCABD44 在同一坐标系中,函数 和 y= k2 x+b 的图象大致如下,则 k1 、k2、b各应满足什么条件?
k2 >0
b >0k1 >0k2 >0
b <0k1 >0k2 <0
b <0k1 <0k2 <0
b >0k1 >0④ 在同一坐标系中,函数 和 y= k2 x+b 的图象大致如下,则 k1 、k2、b各应满足什么条件? 例4 函数 y=kx-k 与 的图象大致是( ) D.xyOyyxB.xyODOOk<0k>0×××√k>0k<0由一次函数增减性得k>0由一次函数与y轴交点知-k>0,
则k<0x提示:可对 k 的正负性进行分类讨论.根据k的值识别函数的图形 7.在同一直角坐标系中,函数 与 y = ax+1
(a≠0) 的图象可能是 ( )
B例5 如图是一次函数 y1=kx+b 和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 . -2< x <0 或 x >3解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,通过函数图形确定字母的取值范围方法总结:对于一些题目,借助函数图象比较大小更加简洁明了.可知-2< x <0 或 x >3. 8. 如图,直线y=k1x+b与双曲线 交于A、B两点,
其横坐标分别为1和5,则不等式 的解集
是_________.1<x<5例6 已知一个正比例函数与一个反比例函数的图象交于点 P (-3,4).
试求出它们的解析式,并画出图象.由于这两个函数的图象交于点 P (-3,4), 则点P 的坐标分别满足这两个解析式.解:设 y=k1x 和 . 所以 , .解得 .利用函数的交点解答问题则这两个函数的解析式分别为 和 ,
它们的图象如图所示.这两个图象有何共同特点?你能求出另外一个交点的坐标吗?说说你发现了什么?【想一想】 9. 反比例函数 的图象与正比例函数 y = 3x 的图象的交点坐标为 . (2,6),(-2,-6)解析:联立两个函数解析式解方程得:
解得:1.(2019?兰州)如图,矩形OABC的顶点B在反比例函数 (x>0)的图象上 S矩形OABC =6,则k= .6ABC2.(2018?岳阳)如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.解:(1)由题意得,k=xy=2×3=6,∴反比例函数的解析式为 .
(2)设B点坐标为(a,b),如图,作AD⊥BC于D,则D(2,b)
∵反比例函数 的图象经过点B(a,b),
∴S△ABC .
设AB的解析式为y=kx+b,
将A(2,3),B(6,1)代入函数解析式,得
解得 ,巩固练习∴ .∴ ,解得a=6,∴ .∴B(6,1).直线AB的解析式为 . D1.(2018?无锡)已知点P(a,m),Q(b,n)都在反比例函数 的图象上,且a<0<b,则下列结论一定正确的是( )
A.m+n<0 B.m+n>0 C.m<n D.m>nD2. (2018?连云港)已知A(﹣4,y1),B(﹣1,y2)是反比例函数 图象上的两个点,则y1与y2的大小关系为_________.y1<y23. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是_______.k>9 1.如图,正比例函数 与反比例函数 的图象
交于点A(2,3).
(1)求k、m的值;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围. (2)由图象可知,正比例函数值大于反比例函数值时:x>2. 解:(1)将A(2,3)分别代入 y=kx 和
可得:3=2k 和
解得: , m=6.2. (2018?贵港)如图,已知反比例函数 (x>0)的图象与一次函数 的图象交于A和B(6,n)两点.
(1)求 k和n的值;
(2)若点C(x,y)也在反比例函数 (x>0)的图象上,求当2≤ x ≤6时,函数值 y的取值范围.解:(1)当x=6时, ,
∴点B的坐标为(6,1).
∵反比例函数 过点B(6,1),
∴k=6×1=6.
(2)∵k=6>0,
∴当x>0时,y随x值增大而减小,
∴当2≤ x ≤6时,1≤ y ≤3. 如图,反比例函数 与一次函数 y =-x + 2 的图象交于 A,B 两点.
(1) 求 A,B 两点的坐标;
解:解得 所以A(-2,4),B(4,-2). 或 作AC⊥x轴于C,BD⊥x轴于D,
则AC=4,BD=2. (2) 求△AOB的面积.解:∵一次函数与x轴的交点为M (2,0), ∴OM=2.MCD∴S△OMB=OM·BD÷2=2×2÷2=2,∴S△OMA=OM·AC÷2=2×4÷2=4,∴S△AOB=S△OMB+S△OMA=2+4=6.面积问题与一次函数的综合反比例函数图象和性质的综合运用面积不变性反比例函数的图象是一个以原点为对称中心的中心对称图形,其与正比例函数的交点关于原点中心对称判断反比例函数和一次函数在同一直角坐标系中的图象,要对系数进行分类讨论,并注意b 的正负
表达式吗? 2. 结合图象分析并掌握反比例函数的性质.1. 会用描点法画反比例函数的图象 .素养目标3. 体会函数的三种表示方法,领会数形结合的思想方法. 画出反比例函数 与 的图象.反比例函数的图象和性质【想一想】 用“描点法”画函数图象都有哪几步?列表描点连线解:列表如下:-1-1.2-1.5-2-3-66321.51.21-2-2.4-3-4-66432.42- 1212注:x的值不能为零,但可以以零为基础,左右均匀、对称地取值。O-2描点:以表中各组对应值作为点的坐标,在直角坐标系内描出各点.56xy4321123456-3-4-1-5-6-1-2-3-4-5-6连线:用光滑的曲线顺次连接各点,即可
得 的图象.x 增大O-256xy4321123456-3-4-1-5-6-1-2-3-4-5-6 观察这两个函数图象,回答问题:【思考】(1) 每个函数图象分
别位于哪些象限?
(2) 在每一个象限内,
随着x的增大,y 如何
变化?你能由它们的
解析式说明理由吗?
y
减
小(3) 对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
(1)由两条曲线组成,且分别位于第一、三象限,它们与 x 轴、y 轴都不相交;
(2)在每个象限内,y 随 x 的增大而减小.反比例函数 (k>0) 的图象和性质:归纳:1. (1)函数 图象在第_______象限,在每个象限内, y随x的增大而 ______. 一、三减小(2)已知反比例函数 在每一个象限内,y随x的增大而减小,则m的取值范围是_____. m>2C 例1 反比例函数 的图象上有两点 A(x1,y1),B(x2, y2),且点A,B 均在该函数图象的第一象限部分,若 x1> x2,则 y1与y2的大小关系为 ( ) 解析:因为8>0,且 A,B 两点均在该函数图象的第一象限部分,根据 x1>x2,可知y1,y2的大小关系.利用反比例函数的性质比较大小观
察
与
思
考 当 k =-2,-4,-6时,反比例函数 的图象,有哪些共同特征? 回顾上面我们利用函数图象,从特殊到一般研究反比例函数 (k>0) 的性质的过程,你能用类似的方法研究反比例函数 (k<0)的图象和性质吗? 反比例函数 (k<0) 的图象和性质:(1)由两条曲线组成,且分别位于第二、四象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而增大.归纳: 反比例函数的图象和性质形状位置增减性图象的发展趋势对称性由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一、三象限内;
当k<0时,两支双曲线分别位于第二、四象限内;当k>0时,在每一象限内, y随x的增大而减小;
当k<0时,在每一象限内, y随x的增大而增大.反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴.(1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数 与 的图象关于x轴对称,也关于y轴对称.2.(1)已知点 A(-3,a),B(-2,b),在双曲线 ,则 a___b(填>、=或<).
>(2)已知点(-1,y1),(2,y2),(3,y3)在反比例函数 (k≠0) 的图象上,则下列结论中正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y1>y2 D.y2>y3>y1B 例2 已知反比例函数 ,在每一象限内,y 随 x 的增大而增大,求a的值.解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.利用反比例函数的图象和性质求字母的值3. 已知反比例函数 在每个象限内,y 随着 x 的增大而减小,求 m 的值.解:由题意得 m2-10=-1,且 3m-8>0.
解得m=3.1.(2018?怀化)函数y=kx﹣3与 (k≠0)在同一坐标系内
的图象可能是( )
A. B. C. D.巩固练习B连接中考2.(2018?德州)给出下列函数:①y=﹣3x+2;② ;③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是( )
A.①③ B.③④ C.②④ D.②③B1.(2018?香坊区)对于反比例函数 ,下列说法
不正确的是( )
A.点(﹣2,﹣1)在它的图象上
B.它的图象在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小C2.(2018?上海)已知反比例函数 (k是常数,k≠1) 的图象有一支在第二象限,那么k的取值范围是________. 3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).(1)k<1(3)y3 >y1>y22. 已知反比例函数 y = mxm2-5,它的两个分支分别在第一、第三象限,求 m 的值.解:因为反比例函数 y = mxm2-5 的两个分支分别在第一、第三象限, 所以有解得 m=2. 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0) 的图象上,若y1<y2,求a的取值范围. 解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
∴a-1>a+1,无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1. ① 当这两点在图象的同一支上时,∵y1<y2,k>0,一、三象限双曲线k﹤0,二、四象限当k>0时,在每一象限
内, y随x的增大而减小当k﹤0时,在每一象限
内, y随x的增大而增大增减性双曲线的两支无限靠近坐标轴,但无交点对称性既是轴对称图形也是中心对称图形???
与 的图象关于x轴对称,也关于y轴对称或或反比例函数的图象和性质
的综合运用返回二、四象限一、三象限位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线 y随x的增大而增大一、三象限在每个象限, y随x的增大而减小二、四象限 y随x的增大而减小在每个象限, y随x的增大而增大
正比例函数和反比例函数的区别用对比的方法去记忆效果如何?3. 深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的思想方法.
1. 理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算中.
2.能解决反比例函数与一次函数的综合问题.素养目标 已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限? y随x的增大如何变化?
(2)点B(3,4)、C( )和D(2,5)是否在这个
函数的图象上?利用待定系数法确定反比例函数解析式
解:(1)因为点A(2,6)在第一象限,所以这个函数的图象在第一、第三象限,在每个象限内,y随x的增大而减小。解:(2)设这个反比例函数的解析式为 ,
因为点A (2,6)在其图象上,所以有 ,
解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
所以反比例函数的解析式为 .方法总结:已知反比例函数图象上一点,可以根据坐标确定点所在的象限,然后确定反比例函数的性质.或用待定系数法求出反比例函数的解析式,再判断图象性质;要判断所给的点是否在该图象上,可以将其坐标代入求得的反比例函数解析式中,若满足左边=右边,则在;若不满足左边=右边,则不在. 【讨论】已知反比例函数图象上的一点,如何确定其图象的性质?以及所给的点是否在该图象上? 1.已知反比例函数 的图象经过点 A (2,3).
(1) 求这个函数的表达式; 解:∵ 反比例函数 的图象经过点 A(2,3),
∴ 把点 A 的坐标代入表达式,得 ,
解得 k = 6.
∴ 这个函数的表达式为 .
(2) 判断点 B (-1,6),C(3,2) 是否在这个函数的图象上,并说明理由;
解:分别把点 B,C 的坐标代入反比例函数的解析式,因为点 B 的坐标不满足该解析式,点C的坐标满足该解析式,所以点 B 不在该函数的图象上,点C 在该函数的图象上. (3) 当 -3< x <-1 时,求 y 的取值范围. 解:∵ 当 x = -3时,y =-2;
当 x = -1时,y =-6,且 k > 0,
∴ 当 x < 0 时,y 随 x 的增大而减小,
∴ 当 -3 < x < -1 时,-6 < y < -2.解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图象的一支在第一象限,则另一支必在第三象限.∵函数的图象在第一、第三象限,∴ m-5>0,解得 m>5. (2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时,b<b′.【思考】根据反比例函数的部分图象,如何确定其完整图象的位置以及比例系数的取值范围?注:由于双曲线的两个分支在两个不同的象限内,因此函数y随x的增减性就不能连续的看,一定要强调“在每一象限内”,否则,笼统说k<0时,y随x的增大而增大,从而出现错误. 2. 如图,是反比例函数 的图象的一个分支,对于
给出的下列说法:
①常数k的取值范围是 ;
②另一个分支在第三象限;
③在函数图象上取点 和 ,
当 时, ;
④在函数图象的某一个分支上取点 和 ,
当 时, .
其中正确的是____________(在横线上填出正确的序号). ① ② ④ 在反比例函数 的图象上分别取点P,Q 向 x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,填写下页表格:
反比例函数中k的几何意义
5PS1 S2 4 4S1=S2S1=S2=k-5-4-3-21432-3-2-4-5-1Q 若在反比例函数 中也用同样的方法分别取 P,Q 两点,填写表格:4 4S1=S2S1=S2=-kS1 S2由前面的探究过程,可以猜想: 若点P是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,矩形AOBP 的面积与k的关系是S矩形 AOBP=|k|.S我们就 k < 0 的情况给出证明:设点 P 的坐标为 (a,b)AB∵点 P (a,b) 在函数 的图
象上,∴ ,即 ab=k.∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;若点 P 在第二象限,则 a<0,b>0,若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP=PB·PA=a· (-b)=-ab=-k.综上,S矩形 AOBP=|k|.自己尝试证明
k > 0的情况. 点 Q 是其图象上的任意一点,作 QA 垂直于 y 轴,作 QB 垂直于x 轴,矩形AOBQ 的面积与 k 的关系是 S矩形AOBQ= .
推理:△QAO与△QBO的面积和 k 的关系是
.Q对于反比例函数 ,AB|k|反比例函数的面积不变性
要
点
归
纳3.如图,点B在反比例函数 (x>0)的图象上,横坐标是1,过点B分别向x轴、y轴作垂线,垂足为A、C,则矩形OABC的面积为( )
A.1 B.2
C.3 D.4
B例1 如图,点A在反比例函数 的图象上,AC垂直 x 轴于点C,且 △AOC 的面积为2,求该反比例函数的表达式.解:设点 A 的坐标为(xA,yA),
∵点A在反比例函数
的图象上,∴ xA·yA=k,
∴反比例函数的表达式为通过图形面积确定k的值∴,∴ k=4,4.如图所示,过反比例函数 (x>0)的图象上一点A,作AB⊥x轴于点B,连接AO.若S△AOB=3,则k的值为( )
A.4 B.5
C.6 D.7
C例2 如图,P,C是函数 (x>0)图象上的任意两点,PA,CD 垂直于x 轴. 设△POA 的面积为S1,则 S1 = ;梯形CEAD 的面积为 S2,则 S1
与 S2 的大小关系是 S1 S2;
△POE 的面积 S3 和 S2 的大小
关系是S2 S3.2S1S2>=S3利用k的性质判断图形面积的关系A. SA >SB>SC B. SA
S四边形ABCD =___.
325?根据k的几何意义求图形的面积方法总结:解决反比例函数有关的面积问题,可以把原图形通过切割、平移等变换,转化为较容易求面积的图形.6. 如图,函数 y=-x 与函数 的图象相交于A,B 两点,过点 A,B 分别作 y 轴的垂线,垂足分别为C,D,则
四边形ACBD的面积为 ( )
A. 2 B. 4
C. 6 D. 8DCABD44 在同一坐标系中,函数 和 y= k2 x+b 的图象大致如下,则 k1 、k2、b各应满足什么条件?
k2 >0
b >0k1 >0k2 >0
b <0k1 >0k2 <0
b <0k1 <0k2 <0
b >0k1 >0④ 在同一坐标系中,函数 和 y= k2 x+b 的图象大致如下,则 k1 、k2、b各应满足什么条件? 例4 函数 y=kx-k 与 的图象大致是( ) D.xyOyyxB.xyODOOk<0k>0×××√k>0k<0由一次函数增减性得k>0由一次函数与y轴交点知-k>0,
则k<0x提示:可对 k 的正负性进行分类讨论.根据k的值识别函数的图形 7.在同一直角坐标系中,函数 与 y = ax+1
(a≠0) 的图象可能是 ( )
B例5 如图是一次函数 y1=kx+b 和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 . -2< x <0 或 x >3解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,通过函数图形确定字母的取值范围方法总结:对于一些题目,借助函数图象比较大小更加简洁明了.可知-2< x <0 或 x >3. 8. 如图,直线y=k1x+b与双曲线 交于A、B两点,
其横坐标分别为1和5,则不等式 的解集
是_________.1<x<5例6 已知一个正比例函数与一个反比例函数的图象交于点 P (-3,4).
试求出它们的解析式,并画出图象.由于这两个函数的图象交于点 P (-3,4), 则点P 的坐标分别满足这两个解析式.解:设 y=k1x 和 . 所以 , .解得 .利用函数的交点解答问题则这两个函数的解析式分别为 和 ,
它们的图象如图所示.这两个图象有何共同特点?你能求出另外一个交点的坐标吗?说说你发现了什么?【想一想】 9. 反比例函数 的图象与正比例函数 y = 3x 的图象的交点坐标为 . (2,6),(-2,-6)解析:联立两个函数解析式解方程得:
解得:1.(2019?兰州)如图,矩形OABC的顶点B在反比例函数 (x>0)的图象上 S矩形OABC =6,则k= .6ABC2.(2018?岳阳)如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.解:(1)由题意得,k=xy=2×3=6,∴反比例函数的解析式为 .
(2)设B点坐标为(a,b),如图,作AD⊥BC于D,则D(2,b)
∵反比例函数 的图象经过点B(a,b),
∴S△ABC .
设AB的解析式为y=kx+b,
将A(2,3),B(6,1)代入函数解析式,得
解得 ,巩固练习∴ .∴ ,解得a=6,∴ .∴B(6,1).直线AB的解析式为 . D1.(2018?无锡)已知点P(a,m),Q(b,n)都在反比例函数 的图象上,且a<0<b,则下列结论一定正确的是( )
A.m+n<0 B.m+n>0 C.m<n D.m>nD2. (2018?连云港)已知A(﹣4,y1),B(﹣1,y2)是反比例函数 图象上的两个点,则y1与y2的大小关系为_________.y1<y23. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是_______.k>9 1.如图,正比例函数 与反比例函数 的图象
交于点A(2,3).
(1)求k、m的值;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围. (2)由图象可知,正比例函数值大于反比例函数值时:x>2. 解:(1)将A(2,3)分别代入 y=kx 和
可得:3=2k 和
解得: , m=6.2. (2018?贵港)如图,已知反比例函数 (x>0)的图象与一次函数 的图象交于A和B(6,n)两点.
(1)求 k和n的值;
(2)若点C(x,y)也在反比例函数 (x>0)的图象上,求当2≤ x ≤6时,函数值 y的取值范围.解:(1)当x=6时, ,
∴点B的坐标为(6,1).
∵反比例函数 过点B(6,1),
∴k=6×1=6.
(2)∵k=6>0,
∴当x>0时,y随x值增大而减小,
∴当2≤ x ≤6时,1≤ y ≤3. 如图,反比例函数 与一次函数 y =-x + 2 的图象交于 A,B 两点.
(1) 求 A,B 两点的坐标;
解:解得 所以A(-2,4),B(4,-2). 或 作AC⊥x轴于C,BD⊥x轴于D,
则AC=4,BD=2. (2) 求△AOB的面积.解:∵一次函数与x轴的交点为M (2,0), ∴OM=2.MCD∴S△OMB=OM·BD÷2=2×2÷2=2,∴S△OMA=OM·AC÷2=2×4÷2=4,∴S△AOB=S△OMB+S△OMA=2+4=6.面积问题与一次函数的综合反比例函数图象和性质的综合运用面积不变性反比例函数的图象是一个以原点为对称中心的中心对称图形,其与正比例函数的交点关于原点中心对称判断反比例函数和一次函数在同一直角坐标系中的图象,要对系数进行分类讨论,并注意b 的正负
