人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):第03章 不 等 式 章末检测
文档属性
| 名称 | 人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):第03章 不 等 式 章末检测 |  | |
| 格式 | zip | ||
| 文件大小 | 578.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 12:27:10 | ||
图片预览




文档简介
第三章 不 等 式
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若不等式的解集是,则的值为
A. B.
C. D.
2.已知,且,若,则一定有
A. B.
C. D.
3.记不等式组所表示的平面区域为,若对任意,不等式恒成立,则实数的取值范围是
A. B.
C. D.
4.已知满足约束条件,则的最小值为
A. B.
C. D.2
5.在中,角,,的对边分别为,,,若,,则的取值范围为
A. B.
C. D.
6.若不等式对任意的恒成立,则实数的取值范围是
A. B.
C. D.
7.已知动点满足,则的最大值是
A.50 B.60
C.70 D.100
8.要制作一个容积为m3,高为m的无盖长方体容器.已知该容器的底面造价是每平方米元,侧面造价是每平方米元,则该容器的最低总造价是
A.元 B.元
C.元 D.元
9.若,满足不等式组,则的最小值为
A. B.
C. D.
10.已知,,且是与的等比中项,则的最小值是
A.2 B.
C.4 D.
11.如果满足且,那么下列选项中不一定成立的是
A. B.
C. D.
12.以方程的两根为三角形两边的长,第三边的长为,则实数的取值范围是
A. B.
C. D.
二、填空题:请将答案填在题中横线上.
13.已知函数,,则的最小值是______________.
14.在中,角,,的对边分别为,,,且,,则的最小值是______________.
15.已知是定义在上的奇函数,且当时,,则不等式的解集为______________.
16.已知实数,满足约束条件,则的取值范围为______________(用区间表示).
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知函数.
(1)当时,求函数的最小值;
(2)当时,不等式恒成立,求实数的最小值.
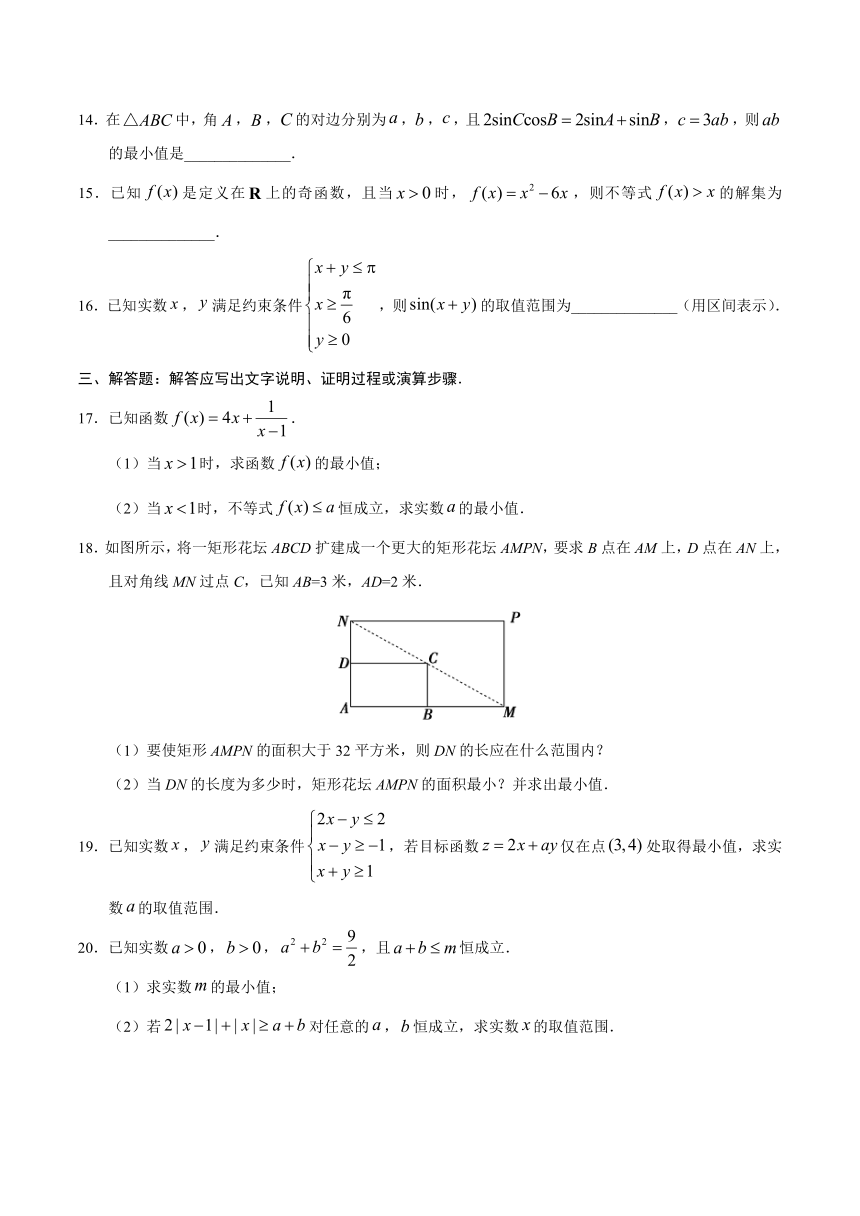
18.如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
(1)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
19.已知实数,满足约束条件,若目标函数仅在点处取得最小值,求实数的取值范围.
20.已知实数,,,且恒成立.
(1)求实数的最小值;
(2)若对任意的,恒成立,求实数的取值范围.
21.已知实数,满足.
(1)求的最大值;
(2)求的最小值;
(3)求的取值范围.
22.已知关于的不等式的解集为.
(1)求实数,的值;
(2)解不关于的不等式.
参考答案
1.【答案】A
【解析】由题意可知,是方程的两个根,所以,,
所以,,所以,故选A.
3.【答案】D
【解析】作出不等式组表示的平面区域(图略),易知当时,,由题可知,所以,故选D.
4.【答案】B
【解析】作出约束条件所表示的平面区域,如图所示(三角形ABC,包括边界),
当目标函数经过点B(0,1)时取得最小值,即的最小值为.故选B.
5.【答案】B
【解析】由题可得,
又,所以,所以,即,
又,所以,故的取值范围为.故选B.
6.【答案】A
【解析】不等式可化为,
因为,所以恒成立,
又在上单调递增,所以,所以,
故实数的取值范围是,故选A.
7.【答案】D
【解析】作出不等式组对应的平面区域如下图中阴影部分所示,
由得,平移直线,
易知当直线经过点C时,直线的纵截距最大,此时最大.
易得,所以.故目标函数的最大值为.故选D.
9.【答案】D
【解析】作出不等式组表示的平面区域如下图中阴影部分所示,
表示平面区域内的点到原点的距离的平方,
易得,由可得,所以,故,故选D.
10.【答案】C
【解析】由题可得,即,,,;
所以(当且仅当且,即,时取等号).故选C.
12.【答案】D
【解析】设方程的两根分别为,,
由题可得,,且,即或.
又,,为三角形三边的长,所以,,
所以,,所以,
所以实数的取值范围是,故选D.
13.【答案】
【解析】因为,所以,
当且仅当,即时等号成立,故的最小值是.
14.【答案】
【解析】∵,且,∴.
∵,∴(当且仅当时取等号),解得,故的最小值是.
16.【答案】
【解析】不等式组表示的平面区域如下图中阴影部分所示,
易得,,,令,可得,平移直线,
易得在点处取得最小值为,与直线重合时取得最大值为,
即的取值范围是,故的取值范围为.
17.【答案】(1);(2).
【解析】(1)由题可得,
因为,所以,
所以(当且仅当时等号成立),
所以函数的最小值为.
(2)因为,所以,
所以(当且仅当时等号成立),
所以函数的最大值为.
因为不等式恒成立,所以,故实数的最小值为.
18.【答案】(1)(0,)∪(6,+∞);(2)米时,矩形花坛的面积最小,最小为24平方米.
【解析】(1)设DN的长为x(x>0)米,则|AN|=(x+2)米.
∵,∴|AM|=,
∴.
(2)矩形花坛的面积为
当且仅当,即时,取等号,
即米时,矩形花坛的面积最小,最小为平方米.
19.【答案】.
【解析】作出不等式组对应的平面区域,如下图中阴影部分所示,
当时,目标函数为,此时在处取得最大值,不满足条件.
当时,由得,
当时,则直线的斜率,
平移直线,得在点处的截距最大,
此时取得最大值,不满足条件.
当时,则直线的斜率,
要使目标函数仅在点处取得最小值,则,
所以,故实数的取值范围为.
20.【答案】(1);(2).
(2)由(1)知,
若对任意的,恒成立,则,
即或或,
解得或,故实数的取值范围为.
21.【答案】(1);(2);(3).
【解析】作出可行域如下图所示,易得A(1,3),B(3,1),C(7,9).
(1)易知可行域内各点均在直线上方,
故,将点C(7,9)代入得的最大值为.
(2)表示可行域内的点到定点M(0,5)的距离的平方,
过M作直线AC的垂线,易知垂足N在线段AC上,
故z的最小值为|MN|2.
(3)表示可行域内任一点与定点Q连线的斜率的两倍,
而,,故z的取值范围为.
22.【答案】(1),;(2)见解析.
(2)由(1)知,,
所以原不等式即,
即,即.
①当,即时,原不等式的解集为;
②当,即时,原不等式的解集为;
③当,即时,原不等式的解集为.
综上所述,当时,原不等式的解集为;当时,原不等式的解集为;当时,原不等式的解集为.
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若不等式的解集是,则的值为
A. B.
C. D.
2.已知,且,若,则一定有
A. B.
C. D.
3.记不等式组所表示的平面区域为,若对任意,不等式恒成立,则实数的取值范围是
A. B.
C. D.
4.已知满足约束条件,则的最小值为
A. B.
C. D.2
5.在中,角,,的对边分别为,,,若,,则的取值范围为
A. B.
C. D.
6.若不等式对任意的恒成立,则实数的取值范围是
A. B.
C. D.
7.已知动点满足,则的最大值是
A.50 B.60
C.70 D.100
8.要制作一个容积为m3,高为m的无盖长方体容器.已知该容器的底面造价是每平方米元,侧面造价是每平方米元,则该容器的最低总造价是
A.元 B.元
C.元 D.元
9.若,满足不等式组,则的最小值为
A. B.
C. D.
10.已知,,且是与的等比中项,则的最小值是
A.2 B.
C.4 D.
11.如果满足且,那么下列选项中不一定成立的是
A. B.
C. D.
12.以方程的两根为三角形两边的长,第三边的长为,则实数的取值范围是
A. B.
C. D.
二、填空题:请将答案填在题中横线上.
13.已知函数,,则的最小值是______________.
14.在中,角,,的对边分别为,,,且,,则的最小值是______________.
15.已知是定义在上的奇函数,且当时,,则不等式的解集为______________.
16.已知实数,满足约束条件,则的取值范围为______________(用区间表示).
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知函数.
(1)当时,求函数的最小值;
(2)当时,不等式恒成立,求实数的最小值.
18.如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
(1)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
19.已知实数,满足约束条件,若目标函数仅在点处取得最小值,求实数的取值范围.
20.已知实数,,,且恒成立.
(1)求实数的最小值;
(2)若对任意的,恒成立,求实数的取值范围.
21.已知实数,满足.
(1)求的最大值;
(2)求的最小值;
(3)求的取值范围.
22.已知关于的不等式的解集为.
(1)求实数,的值;
(2)解不关于的不等式.
参考答案
1.【答案】A
【解析】由题意可知,是方程的两个根,所以,,
所以,,所以,故选A.
3.【答案】D
【解析】作出不等式组表示的平面区域(图略),易知当时,,由题可知,所以,故选D.
4.【答案】B
【解析】作出约束条件所表示的平面区域,如图所示(三角形ABC,包括边界),
当目标函数经过点B(0,1)时取得最小值,即的最小值为.故选B.
5.【答案】B
【解析】由题可得,
又,所以,所以,即,
又,所以,故的取值范围为.故选B.
6.【答案】A
【解析】不等式可化为,
因为,所以恒成立,
又在上单调递增,所以,所以,
故实数的取值范围是,故选A.
7.【答案】D
【解析】作出不等式组对应的平面区域如下图中阴影部分所示,
由得,平移直线,
易知当直线经过点C时,直线的纵截距最大,此时最大.
易得,所以.故目标函数的最大值为.故选D.
9.【答案】D
【解析】作出不等式组表示的平面区域如下图中阴影部分所示,
表示平面区域内的点到原点的距离的平方,
易得,由可得,所以,故,故选D.
10.【答案】C
【解析】由题可得,即,,,;
所以(当且仅当且,即,时取等号).故选C.
12.【答案】D
【解析】设方程的两根分别为,,
由题可得,,且,即或.
又,,为三角形三边的长,所以,,
所以,,所以,
所以实数的取值范围是,故选D.
13.【答案】
【解析】因为,所以,
当且仅当,即时等号成立,故的最小值是.
14.【答案】
【解析】∵,且,∴.
∵,∴(当且仅当时取等号),解得,故的最小值是.
16.【答案】
【解析】不等式组表示的平面区域如下图中阴影部分所示,
易得,,,令,可得,平移直线,
易得在点处取得最小值为,与直线重合时取得最大值为,
即的取值范围是,故的取值范围为.
17.【答案】(1);(2).
【解析】(1)由题可得,
因为,所以,
所以(当且仅当时等号成立),
所以函数的最小值为.
(2)因为,所以,
所以(当且仅当时等号成立),
所以函数的最大值为.
因为不等式恒成立,所以,故实数的最小值为.
18.【答案】(1)(0,)∪(6,+∞);(2)米时,矩形花坛的面积最小,最小为24平方米.
【解析】(1)设DN的长为x(x>0)米,则|AN|=(x+2)米.
∵,∴|AM|=,
∴.
(2)矩形花坛的面积为
当且仅当,即时,取等号,
即米时,矩形花坛的面积最小,最小为平方米.
19.【答案】.
【解析】作出不等式组对应的平面区域,如下图中阴影部分所示,
当时,目标函数为,此时在处取得最大值,不满足条件.
当时,由得,
当时,则直线的斜率,
平移直线,得在点处的截距最大,
此时取得最大值,不满足条件.
当时,则直线的斜率,
要使目标函数仅在点处取得最小值,则,
所以,故实数的取值范围为.
20.【答案】(1);(2).
(2)由(1)知,
若对任意的,恒成立,则,
即或或,
解得或,故实数的取值范围为.
21.【答案】(1);(2);(3).
【解析】作出可行域如下图所示,易得A(1,3),B(3,1),C(7,9).
(1)易知可行域内各点均在直线上方,
故,将点C(7,9)代入得的最大值为.
(2)表示可行域内的点到定点M(0,5)的距离的平方,
过M作直线AC的垂线,易知垂足N在线段AC上,
故z的最小值为|MN|2.
(3)表示可行域内任一点与定点Q连线的斜率的两倍,
而,,故z的取值范围为.
22.【答案】(1),;(2)见解析.
(2)由(1)知,,
所以原不等式即,
即,即.
①当,即时,原不等式的解集为;
②当,即时,原不等式的解集为;
③当,即时,原不等式的解集为.
综上所述,当时,原不等式的解集为;当时,原不等式的解集为;当时,原不等式的解集为.
