人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):专题1.1.1 正弦定理
文档属性
| 名称 | 人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):专题1.1.1 正弦定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 565.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 12:28:19 | ||
图片预览




文档简介
第一章 解三角形
1.1 正弦定理和余弦定理
1.1.1 正弦定理
知识
1.正弦定理
在中,若角A,B,C对应的三边分别是a,b,c,则各边和它所对角的正弦的比相等,即____________.正弦定理对任意三角形都成立.
2.解三角形
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的____________.已知三角形的几个元素求其他元素的过程叫做____________.
知识参考答案:
1. 2.元素 解三角形
重点
重点
正弦定理的变形和推广、正弦定理在解三角形中的应用
难点
三角形解的个数的探究、三角形形状的判断
易错
解三角形时要明确角的取值范围,同时注意对角的讨论
正弦定理的常见变形及推广
(1).
(2).
(3).
(4)正弦定理的推广:,其中为外接圆的半径.
(1)已知ABC中,,则=_____________;
(2)已知ABC中,A,,则=_____________.
【答案】(1);(2)2.
【解析】(1)根据正弦定理的变形,可得.
(2)方法1:设,则有
从而,又,所以=2.
方法2:根据正弦定理的变形,可得.
【名师点睛】熟记正弦定理的变形,可使解题过程更加简捷,从而达到事半功倍的效果.
在中,求证:.
【答案】证明见解析.
【解析】设外接圆的半径为R,则 于是
所以.
【解题技巧】的两种变形的应用:
(1)(边化角);
(2)(角化边).
正弦定理在解三角形中的应用、三角形解的个数的探究
1.正弦定理可以用来解决下列两类解三角形的问题:
(1)已知两角和任意一边,求其他的边和角;
(2)已知两边和其中一边的对角,求其他的边和角.
2.三角形解的个数的探究(以已知和解三角形为例)
(1)从代数角度来看
①若,则满足条件的三角形的个数为0,即无解;
②若,则满足条件的三角形的个数为1;
③若,则满足条件的三角形的个数为1或2.
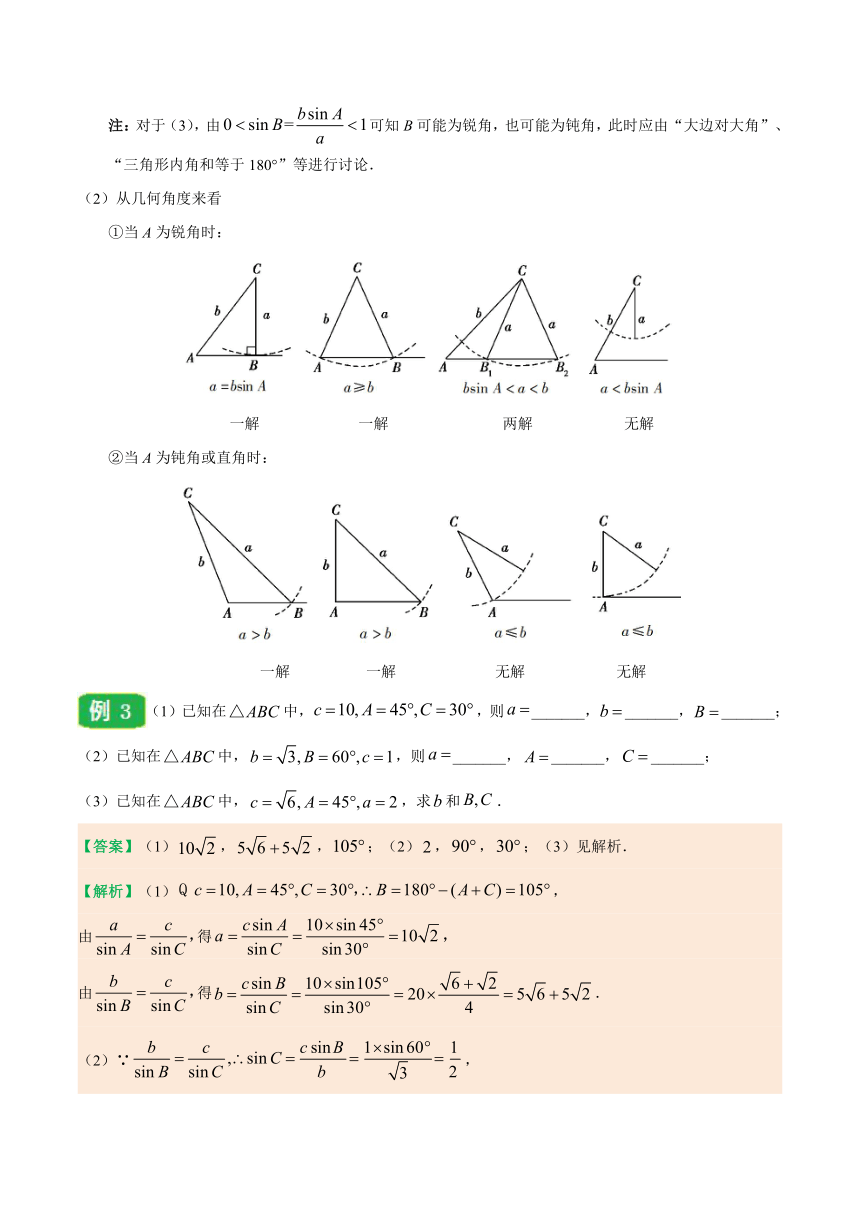
注:对于(3),由可知B可能为锐角,也可能为钝角,此时应由“大边对大角”、“三角形内角和等于180°”等进行讨论.
(2)从几何角度来看
①当A为锐角时:
一解 一解 两解 无解
②当A为钝角或直角时:
一解 一解 无解 无解
(1)已知在中,,则_______,_______,_______;
(2)已知在中,,则_______,_______,_______;
(3)已知在中,,求和.
【答案】(1),,;(2),,;(3)见解析.
【解析】(1),
由得
由得.
(2)∵,
,为锐角,,∴.
(3),
或,
当时,,
当时,.
或.
【解题技巧】(1)已知三角形的两角与一边解三角形时,由三角形内角和定理可以计算出三角形的另一角,由正弦定理可计算出三角形的另两边.
(2)已知两边和其中一边的对角解三角形时,先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中“大边对大角”看能否判断所求这个角是锐角,①当已知的角为大边所对的角时,则能判断另一边所对的角为锐角;②当已知的角为小边所对的角时,则不能判断,此时就有两解,再分别求解即可;③然后由三角形内角和定理求出第三个角;④最后根据正弦定理求出第三条边.
三角形形状的判断
判断三角形形状的常用方法——边化角,已知条件中同时包含边角关系,判断三角形形状时,将边化为角,从三角变换的角度来研究角的关系和特征,进而判断三角形的形状.一般来说,这种方法能够判断的三角形都是特殊的三角形,如直角三角形、等腰三角形、等边三角形、等腰直角三角形.
在中,已知,且,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
【答案】B
【解析】设的外接圆半径为,由正弦定理的推广,得,,
代入,可得,即.
因为,所以,
即.
由正弦定理的推广可得,所以,
由及可得,所以是直角三角形.
故选B.
【名师点睛】注意到a,b,c在条件式中是齐次线性关系,因此可以考虑利用正弦定理将边化为角.通过角的特征或者关系来判断三角形的形状.
忽略角的取值范围而出错
在中,若,求的取值范围.
【错解】由正弦定理,可得
,
,
由,可得.
故的取值范围为.
【错因分析】错解中没有考虑角的取值范围,误认为角的取值范围为.
【正解】由正弦定理可得
,
,
,即,
故的取值范围为.
【名师点睛】解三角形时要注意三角形的内角为正角且必须满足三角形内角和定理,这是解题中的隐含条件,应特别注意.
忽略对角的讨论而出错
已知在中, 求角和边.
【错解】由正弦定理可得 ,
,,.
【错因分析】错解中由正弦定理求出角A的正弦值后误认为角A是锐角,从而导致错误.
【正解】由正弦定理得
或.
当时,,
当时,,
.
综上,或.
【名师点睛】在中,已知两边和其中一边的对角解三角形时,可先用正弦定理求出另一边的对角,此时解的个数可能不确定,应注意讨论,避免漏解导致错误.
基础训练
1.在中,角,,的对边分别为,,,,则
A. B.
C. D.
2.在中,角,,的对边分别为,,,若,,,则
A.或 B.
C. D.
3.在中,若∠A=60°,∠B=45°,BC=,则AC=
A. B.
C. D.
4.在中,角A,B,C的对边分别为a,b,c,已知A:B:C=1:2:3,则a:b:c=
A.1:2:3 B.1:2:
C.1::2 D.2::1
5.在中,角A,B,C的对边分别为a,b,c,,,,则
A. B.
C. D.
6.在中,角A,B,C的对边分别为a,b,c,若,则的形状为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
7.在中,角A,B,C的对边分别为a,b,c,,则此三角形解的个数为
A. B.
C. D.不能确定
8.已知中,角A,B,C的对边分别为a,b,c,且cosA:cosB=b:a,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
9.在中,角A,B,C的对边分别为a,b,c,若,,,则______________.
10.在中,角A,C的对边分别为a,c,其中,,则角______________.
11.在中,若B=30°,AB=2,AC=2,则的周长为______________.
12.的内角A,B,C的对边分别为a,b,c,己知?=90°,+=,求.
能力提升
13.在中,角A,B,C的对边分别为a,b,c,若a=b,A=2B,则cosB=
A. B.
C. D.
14.在中,角A,B,C的对边分别为a,b,c,已知,则
A. B.
C. D.
15.在中,角A,B,C的对边分别为a,b,c,已知,则角B等于
A. B.
C.或 D.以上都不正确
16.在中,角A,B,C的对边为a,b,c,若,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
17.在中,角A,B,C的对边分别为a,b,c,若,则是
A.有一内角是30°的三角形 B.等边三角形
C.等腰直角三角形 D.有一内角是30°的等腰三角形
18.在中,已知,则边长
A.或 B.
C.2 D.
19.在中,已知,,则______________.
20.如图所示,在一个坡度一定的山坡的顶上有一高度为25的建筑物.为了测量该山坡相对于水平地面的坡角,在山坡的处测得,沿山坡前进50到达处,又测得.根据以上数据计算可得______________.
21.如图,在中,点在边上,.
(1)求的值;
(2)若,求的长.
真题练习
22.(2019山东模拟)在中,角A,B,C的对边分别为,,.若为锐角三角形,且满足,则下列等式成立的是
A. B.
C. D.
23.(2018新课标全国Ⅰ文)△ABC的内角A,B,C的对边分别为a,b,c.已知,a=2,c=,则C=
A. B.
C. D.
24.(2019重庆模拟)的内角A,B,C的对边分别为a,b,c,若,则______________.
25.(2017新课标全国Ⅲ文)的内角A,B,C的对边分别为a,b,c.已知C=60°,b=,c=3,则A=______________.
26.(2018北京理)在中,,,.
(1)求;
(2)求边上的高.
参考答案
1.【答案】D
【解析】∵,由得故选D.
2.【答案】B
【解析】在中,由得,由于,所以,所以,故选B.
3.【答案】B
【解析】由正弦定理得,所以AC=故选B.
4.【答案】C
【解析】因为在中,A+B+C=π,且A:B:C=1:2:3,所以A=,B=,C=,由正弦定理的变形,得a:b:c=sinA:sinB:sinC1::2.故选C.
6.【答案】B
【解析】由已知可得,∴,∴,∴,三角形为直角三角形.故选B.
7.【答案】C
【解析】由正弦定理可得,因为,所以,所以角可能是锐角,也可能是钝角,所以此三角形有两解,故选C.
8.【答案】D
【解析】由正弦定理可得,即sinAcosA=sinBcosB,所以sin2A=sin2B,即2A=2B或2A+2B=π,即A=B或A+B=,故是等腰或直角三角形.故选D.
9.【答案】
【解析】∵,,∴,∵,∴,∴.
10.【答案】
【解析】由正弦定理可得,即,所以或,又,所以.
12.【答案】.
【解析】由正弦定理可得,又由于,
故,
即.
因为,所以,即.
13.【答案】B
【解析】由正弦定理,得,所以a=b可化为=.
又A=2B,所以=,所以cosB=.故选B.
14.【答案】D
【解析】在中,由正弦定理可得,又,所以,故选D.
15.【答案】A
【解析】在中,∵,∴,又,∴,∴,故选A.
16.【答案】D
【解析】由正弦定理和已知条件可得,
所以 即,
所以或,即或.故是等腰三角形或直角三角形.
故选D.
18.【答案】A
【解析】由正弦定理可得,,
在中,,或.
当时,,;
当时,,此时.
综上,可得或.故选A.
19.【答案】或
【解析】由正弦定理得,得,
由,得,所以或,从而或.
21.【答案】(1);(2).
【解析】(1)因为,所以.
又,所以,
所以.
(2)在中,由,可得.
22.【答案】A
【解析】由题意知,
所以,故选A.
23.【答案】B
【解析】由可得,即,所以.
由正弦定理可得,即,因为,所以,
所以,故选B.
24.【答案】
【解析】由正弦定理可得.
25.【答案】
【解析】由正弦定理,可得,结合可得,则.
26.【答案】(1);(2)AC边上的高为.
【解析】(1)在中,因为,所以,所以.
由正弦定理,所以.
因为,所以,所以.
(2)在中,.
如图所示,在中,,所以,
所以边上的高为.
1.1 正弦定理和余弦定理
1.1.1 正弦定理
知识
1.正弦定理
在中,若角A,B,C对应的三边分别是a,b,c,则各边和它所对角的正弦的比相等,即____________.正弦定理对任意三角形都成立.
2.解三角形
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的____________.已知三角形的几个元素求其他元素的过程叫做____________.
知识参考答案:
1. 2.元素 解三角形
重点
重点
正弦定理的变形和推广、正弦定理在解三角形中的应用
难点
三角形解的个数的探究、三角形形状的判断
易错
解三角形时要明确角的取值范围,同时注意对角的讨论
正弦定理的常见变形及推广
(1).
(2).
(3).
(4)正弦定理的推广:,其中为外接圆的半径.
(1)已知ABC中,,则=_____________;
(2)已知ABC中,A,,则=_____________.
【答案】(1);(2)2.
【解析】(1)根据正弦定理的变形,可得.
(2)方法1:设,则有
从而,又,所以=2.
方法2:根据正弦定理的变形,可得.
【名师点睛】熟记正弦定理的变形,可使解题过程更加简捷,从而达到事半功倍的效果.
在中,求证:.
【答案】证明见解析.
【解析】设外接圆的半径为R,则 于是
所以.
【解题技巧】的两种变形的应用:
(1)(边化角);
(2)(角化边).
正弦定理在解三角形中的应用、三角形解的个数的探究
1.正弦定理可以用来解决下列两类解三角形的问题:
(1)已知两角和任意一边,求其他的边和角;
(2)已知两边和其中一边的对角,求其他的边和角.
2.三角形解的个数的探究(以已知和解三角形为例)
(1)从代数角度来看
①若,则满足条件的三角形的个数为0,即无解;
②若,则满足条件的三角形的个数为1;
③若,则满足条件的三角形的个数为1或2.
注:对于(3),由可知B可能为锐角,也可能为钝角,此时应由“大边对大角”、“三角形内角和等于180°”等进行讨论.
(2)从几何角度来看
①当A为锐角时:
一解 一解 两解 无解
②当A为钝角或直角时:
一解 一解 无解 无解
(1)已知在中,,则_______,_______,_______;
(2)已知在中,,则_______,_______,_______;
(3)已知在中,,求和.
【答案】(1),,;(2),,;(3)见解析.
【解析】(1),
由得
由得.
(2)∵,
,为锐角,,∴.
(3),
或,
当时,,
当时,.
或.
【解题技巧】(1)已知三角形的两角与一边解三角形时,由三角形内角和定理可以计算出三角形的另一角,由正弦定理可计算出三角形的另两边.
(2)已知两边和其中一边的对角解三角形时,先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中“大边对大角”看能否判断所求这个角是锐角,①当已知的角为大边所对的角时,则能判断另一边所对的角为锐角;②当已知的角为小边所对的角时,则不能判断,此时就有两解,再分别求解即可;③然后由三角形内角和定理求出第三个角;④最后根据正弦定理求出第三条边.
三角形形状的判断
判断三角形形状的常用方法——边化角,已知条件中同时包含边角关系,判断三角形形状时,将边化为角,从三角变换的角度来研究角的关系和特征,进而判断三角形的形状.一般来说,这种方法能够判断的三角形都是特殊的三角形,如直角三角形、等腰三角形、等边三角形、等腰直角三角形.
在中,已知,且,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
【答案】B
【解析】设的外接圆半径为,由正弦定理的推广,得,,
代入,可得,即.
因为,所以,
即.
由正弦定理的推广可得,所以,
由及可得,所以是直角三角形.
故选B.
【名师点睛】注意到a,b,c在条件式中是齐次线性关系,因此可以考虑利用正弦定理将边化为角.通过角的特征或者关系来判断三角形的形状.
忽略角的取值范围而出错
在中,若,求的取值范围.
【错解】由正弦定理,可得
,
,
由,可得.
故的取值范围为.
【错因分析】错解中没有考虑角的取值范围,误认为角的取值范围为.
【正解】由正弦定理可得
,
,
,即,
故的取值范围为.
【名师点睛】解三角形时要注意三角形的内角为正角且必须满足三角形内角和定理,这是解题中的隐含条件,应特别注意.
忽略对角的讨论而出错
已知在中, 求角和边.
【错解】由正弦定理可得 ,
,,.
【错因分析】错解中由正弦定理求出角A的正弦值后误认为角A是锐角,从而导致错误.
【正解】由正弦定理得
或.
当时,,
当时,,
.
综上,或.
【名师点睛】在中,已知两边和其中一边的对角解三角形时,可先用正弦定理求出另一边的对角,此时解的个数可能不确定,应注意讨论,避免漏解导致错误.
基础训练
1.在中,角,,的对边分别为,,,,则
A. B.
C. D.
2.在中,角,,的对边分别为,,,若,,,则
A.或 B.
C. D.
3.在中,若∠A=60°,∠B=45°,BC=,则AC=
A. B.
C. D.
4.在中,角A,B,C的对边分别为a,b,c,已知A:B:C=1:2:3,则a:b:c=
A.1:2:3 B.1:2:
C.1::2 D.2::1
5.在中,角A,B,C的对边分别为a,b,c,,,,则
A. B.
C. D.
6.在中,角A,B,C的对边分别为a,b,c,若,则的形状为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
7.在中,角A,B,C的对边分别为a,b,c,,则此三角形解的个数为
A. B.
C. D.不能确定
8.已知中,角A,B,C的对边分别为a,b,c,且cosA:cosB=b:a,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
9.在中,角A,B,C的对边分别为a,b,c,若,,,则______________.
10.在中,角A,C的对边分别为a,c,其中,,则角______________.
11.在中,若B=30°,AB=2,AC=2,则的周长为______________.
12.的内角A,B,C的对边分别为a,b,c,己知?=90°,+=,求.
能力提升
13.在中,角A,B,C的对边分别为a,b,c,若a=b,A=2B,则cosB=
A. B.
C. D.
14.在中,角A,B,C的对边分别为a,b,c,已知,则
A. B.
C. D.
15.在中,角A,B,C的对边分别为a,b,c,已知,则角B等于
A. B.
C.或 D.以上都不正确
16.在中,角A,B,C的对边为a,b,c,若,则是
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
17.在中,角A,B,C的对边分别为a,b,c,若,则是
A.有一内角是30°的三角形 B.等边三角形
C.等腰直角三角形 D.有一内角是30°的等腰三角形
18.在中,已知,则边长
A.或 B.
C.2 D.
19.在中,已知,,则______________.
20.如图所示,在一个坡度一定的山坡的顶上有一高度为25的建筑物.为了测量该山坡相对于水平地面的坡角,在山坡的处测得,沿山坡前进50到达处,又测得.根据以上数据计算可得______________.
21.如图,在中,点在边上,.
(1)求的值;
(2)若,求的长.
真题练习
22.(2019山东模拟)在中,角A,B,C的对边分别为,,.若为锐角三角形,且满足,则下列等式成立的是
A. B.
C. D.
23.(2018新课标全国Ⅰ文)△ABC的内角A,B,C的对边分别为a,b,c.已知,a=2,c=,则C=
A. B.
C. D.
24.(2019重庆模拟)的内角A,B,C的对边分别为a,b,c,若,则______________.
25.(2017新课标全国Ⅲ文)的内角A,B,C的对边分别为a,b,c.已知C=60°,b=,c=3,则A=______________.
26.(2018北京理)在中,,,.
(1)求;
(2)求边上的高.
参考答案
1.【答案】D
【解析】∵,由得故选D.
2.【答案】B
【解析】在中,由得,由于,所以,所以,故选B.
3.【答案】B
【解析】由正弦定理得,所以AC=故选B.
4.【答案】C
【解析】因为在中,A+B+C=π,且A:B:C=1:2:3,所以A=,B=,C=,由正弦定理的变形,得a:b:c=sinA:sinB:sinC1::2.故选C.
6.【答案】B
【解析】由已知可得,∴,∴,∴,三角形为直角三角形.故选B.
7.【答案】C
【解析】由正弦定理可得,因为,所以,所以角可能是锐角,也可能是钝角,所以此三角形有两解,故选C.
8.【答案】D
【解析】由正弦定理可得,即sinAcosA=sinBcosB,所以sin2A=sin2B,即2A=2B或2A+2B=π,即A=B或A+B=,故是等腰或直角三角形.故选D.
9.【答案】
【解析】∵,,∴,∵,∴,∴.
10.【答案】
【解析】由正弦定理可得,即,所以或,又,所以.
12.【答案】.
【解析】由正弦定理可得,又由于,
故,
即.
因为,所以,即.
13.【答案】B
【解析】由正弦定理,得,所以a=b可化为=.
又A=2B,所以=,所以cosB=.故选B.
14.【答案】D
【解析】在中,由正弦定理可得,又,所以,故选D.
15.【答案】A
【解析】在中,∵,∴,又,∴,∴,故选A.
16.【答案】D
【解析】由正弦定理和已知条件可得,
所以 即,
所以或,即或.故是等腰三角形或直角三角形.
故选D.
18.【答案】A
【解析】由正弦定理可得,,
在中,,或.
当时,,;
当时,,此时.
综上,可得或.故选A.
19.【答案】或
【解析】由正弦定理得,得,
由,得,所以或,从而或.
21.【答案】(1);(2).
【解析】(1)因为,所以.
又,所以,
所以.
(2)在中,由,可得.
22.【答案】A
【解析】由题意知,
所以,故选A.
23.【答案】B
【解析】由可得,即,所以.
由正弦定理可得,即,因为,所以,
所以,故选B.
24.【答案】
【解析】由正弦定理可得.
25.【答案】
【解析】由正弦定理,可得,结合可得,则.
26.【答案】(1);(2)AC边上的高为.
【解析】(1)在中,因为,所以,所以.
由正弦定理,所以.
因为,所以,所以.
(2)在中,.
如图所示,在中,,所以,
所以边上的高为.
