人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):专题1.2 应用举例
文档属性
| 名称 | 人教版高中数学必修五知识讲解,巩固练习(教学资料,补习资料):专题1.2 应用举例 |

|
|
| 格式 | zip | ||
| 文件大小 | 893.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 12:28:40 | ||
图片预览




文档简介
1.2 应用举例
知识
1.解三角形应用题的基本思想
解三角形应用题时,通常都要根据题意,从实际问题中抽象出一个或几个三角形,然后通过解三角形,得到实际问题的解,求解的关键是将实际问题转化为___________问题.
2.运用正弦定理、余弦定理解决实际问题的基本步骤
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
3.三角形面积公式
(1)三角形的高的公式:hA=bsinC=csinB,hB=csinA=asinC,hC=asinB=bsinA.
(2)三角形的面积公式:S=absinC,S=___________,S=___________.
知识参考答案:
1.解三角形
3.bcsinA casinB
重点
重点
从实际问题中抽象出一个或几个三角形,然后逐个解三角形,得到实际问题的解;利用三角形的面积公式解决与面积有关的问题
难点
测量距离、高度、角度问题中数学模型的建立,利用正弦定理、余弦定理求证简单的证明题
易错
解题时应由题意准确画出示意图,容易忽略图形的多种画法从而导致错误
测量距离问题
当的长度不可直接测量时,求,之间的距离有以下三种类型.
(1)如图1,A,B之间不可达也不可视
计算方法:测量,及角,由余弦定理可得.
(2)如图2,B,C与点A可视但不可达
计算方法:测量,角,角,则,由正弦定理可得.
(3)如图3,C,D与点A,B均可视不可达,
计算方法:测量,在中由正弦定理求,
在中由正弦定理求,在中由余弦定理求.
图1 图2 图3
如下图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为______________km.
【答案】
【解析】因为∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,所以∠DAC=60°,AC=DC=,
因为在中,∠DBC=45°,所以,所以BC=.
在中,由余弦定理得AB2=AC2+BC2-2AC·BC·cos45°=,
所以AB=,所以A,B两点间的距离为km.
【名师点睛】在解含有两个或两个以上的三角形的问题时,首先应根据条件应用正、余弦定理或三角形内角和定理在一个三角形中求解边和角,然后在此基础上求解另一个三角形,依此类推.首选哪一个三角形至关重要,原则是首选的三角形应与其他三角形有一定联系,且方便求解.
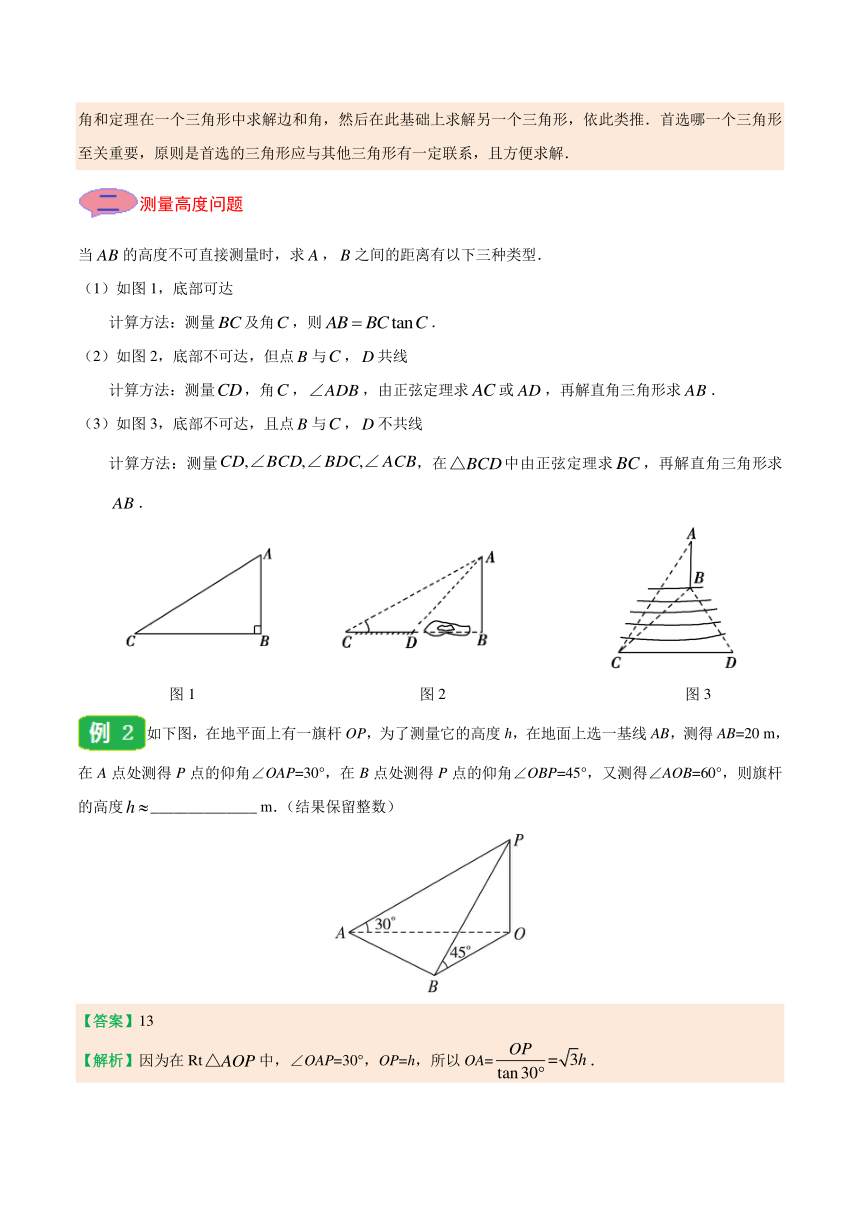
测量高度问题
当的高度不可直接测量时,求,之间的距离有以下三种类型.
(1)如图1,底部可达
计算方法:测量及角,则.
(2)如图2,底部不可达,但点与,共线
计算方法:测量,角,,由正弦定理求或,再解直角三角形求.
(3)如图3,底部不可达,且点与,不共线
计算方法:测量,在中由正弦定理求,再解直角三角形求.
图1 图2 图3
如下图,在地平面上有一旗杆OP,为了测量它的高度h,在地面上选一基线AB,测得AB=20 m,在A点处测得P点的仰角∠OAP=30°,在B点处测得P点的仰角∠OBP=45°,又测得∠AOB=60°,则旗杆的高度______________ m.(结果保留整数)
【答案】13
【解析】因为在Rt中,∠OAP=30°,OP=h,所以OA=.
在Rt中,∠OBP=45°,所以OB=h.
在中,AB=20,∠AOB=60°,由余弦定理得AB2=OA2+OB2-2×OA×OBcos60°,
即202=2+h2-2×h×h×,解得h2=≈176.4,所以h ≈13.
故旗杆的高度约为13 m.
【名师点睛】高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形或者在空间构造三棱锥,再依据条件利用正、余弦定理解其中的一个或者几个三角形,从而求出所需测量物体的高度.
测量角度问题
测量角度问题主要涉及海上、空中的追及与拦截,此时问题涉及方向角、方位角等概念,若是观察建筑物、山峰等,则会涉及俯角、仰角等概念.
如图,某船在A处看灯塔S在北偏东30°方向,它以每小时30海里的速度向正北方向航行,经过40分钟航行到B处,看灯塔S在北偏东75°方向,则此时该船到灯塔S的距离约为______________海里.(精确到0.01海里)
【答案】
【解析】由题图可知,在中,∠ABS=180°-75°=105°,∠BAS=30°,
所以∠ASB=45°,AB=30×=20(海里),由正弦定理,得,
故BS=,故该船到灯塔S的距离约为海里.
【名师点睛】解决此类问题的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.解题时应认真审题,结合图形去选择正、余弦定理,这是最重要的一步.
三角形的面积计算问题
在求三角形的面积时,若存在三角形边长平方和的情况,一般联想到用余弦定理解决;若存在边长乘积时,一般联想到用公式S=absinC=bcsinA=casinB解决.
在中,角A,B,C对应的三边分别是a,b,c,已知a=2,b=2,的面积S=,则
A. B.
C. D.或
【答案】D
【解析】由S=absinC=×2×2sinC=得sinC=,所以C=30°或150°.
①当C=30°时,由余弦定理得c2=a2+b2-2abcosC=(2)2+22-2×2×2cos30°=4,所以c=2.
②当C=150°时,由余弦定理得c2=a2+b2-2abcosC=(2)2+22-2×2×2cos150°=28,所以2.
综上,或.故选D.
【名师点睛】在解三角形面积的问题中,要注意三角形面积公式与余弦定理的结合.
三角形中边角关系恒等式的证明
在中,求证:.
【答案】证明见解析.
【解析】根据正弦定理,可设,显然 k ≠0,
所以,左边==右边,
所以.
【名师点睛】有关三角形的证明问题,主要涉及三角形的边和角的三角函数关系.从某种意义上看,这类问题就是有目标地对含边和角的式子进行化简的问题,所以解题思路与判断三角形的形状类似:将边化为角或者将角化为边.
基础训练
1.已知A,B两地的距离为5km,B,C两地的距离为10km,经测量可知,,则A,C两地的距离为
A.5km B.km
C.km D.km
2.如图,设,两点在河的两岸,一测量者在的同侧,在所在的河岸边选定的一点,测出的距离为,,后,就可以计算出,两点的距离为
A. B.
C. D.
3.某人向正东方向走了xkm后向右转了150°,然后沿新方向走了3km,结果离出发点恰好为km,那么x的值为
A. B.2
C.3 D.2或
4.如图,一艘轮船以每小时60海里的速度自A沿南偏东的方向直线航行,30分钟后到达B处,在C处有一座灯塔,轮船在A处观察灯塔,其方向是南偏东,在B处观察灯塔,其方向是北偏东,那么B,C间的距离是
A.海里 B.海里
C.海里 D.海里
5.若锐角三角形的面积为,且,,则
A. B.
C. D.
6.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是
A. B.
C. D.
7.一架直升飞机在600m的高空中,测得地面上一座塔的塔顶与塔底的俯角分别是和,则塔高为
A. B.
C. D.
8.一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8海里,则灯塔S在B处的
A.北偏东75° B.北偏东75°或东偏南75°
C.东偏南75° D.以上方位都不对
9.在中,若,则_____________.
10.江岸边有一炮台高,江中有两条船,船与炮台底部在同一水平面上,由炮台顶部测得两船的俯角分别为和,而且两条船与炮台底部连线成角,则两条船相距_____________.
11.甲船在岛B的正南A处,AB=10km,甲船以每小时4km的速度向正北航行,同时,乙船自B出发以每小时6km的速度向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间是_____________h.
12.如图所示,在山顶上有一座塔,在山底测得塔顶的仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得塔顶的仰角∠DSB=75°,则塔高BD=_____________米.
13.在中,角,,所对的边分别为,,,且.
(1)求角;
(2)若,求及的面积.
14.在中,角,,所对的边分别为,且.
(1)若,,求的值;
(2)若,且的面积,求和的值.
能力提升
15.已知的周长为20,面积为10,A=60°,则BC的长等于
A.5 B.6
C.7 D.8
16.如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C、D两处用测角仪测得塔顶部B处的仰角分别是和,如果C、D间的距离是,测角仪高为,则塔高为
A. B.
C. D.
17.在中,角,,的对边分别为,,,若,,且,则
A.2 B.3
C.4 D.5
18.两船同时从港出发,甲船以每小时20海里的速度向北偏东的方向航行,乙船以每小时12海里的速度向北偏西方向航行,一小时后两船相距_____________海里.
19.如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,则此舰____________触礁的危险.(填“有”或“没有”)
20.已知锐角三角形的内角,,的对边分别为,,,若,,则面积的取值范围是_____________.
21.在中,为边上一点,,,.
图1 图2
(1)如图1,若,求的大小;
(2)如图2,若,求的面积.
22.如图,渔船甲位于岛屿A的南偏西方向的B处,且与岛屿A相距18海里,渔船乙以15海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东的方向追赶渔船乙,刚好用2h追上,此时到达C处.
(1)求渔船甲的速度;
(2)求的值.
23.某港口要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的北偏西且与该港口相距海里的处,并正以海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以海里/小时的航行速度匀速行驶,经过小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在分钟内(含分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(3)是否存在,使得小艇以海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定的取值范围;若不存在,请说明理由.
24.在中,角,,的对边分别为,,,已知.
(1)求角的大小;
(2)若,求的面积的最大值.
真题练习
25.(2018新课标全国Ⅲ文理)的内角,,的对边分别为,,,若的面积为,则
A. B.
C. D.
26.(2018新课标全国Ⅰ文)的内角,,的对边分别为,,,已知,,则的面积为_____________.
27.(2018北京文)若的面积为,且为钝角,则_____________;的取值范围是_____________.
28.(2019浙江模拟)已知△ABC,AB=AC=4,BC=2.?点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是_____________,cos∠BDC=_____________.
29.(2019浙江模拟)的内角A,B,C的对边分别为a,b,c,已知的面积为.
(1)求sin Bsin C;
(2)若6cos Bcos C=1,a=3,求的周长.
30.(2019上海模拟)的内角A,B,C的对边分别为a,b,c,已知.
(1)求;
(2)若,的面积为,求.
参考答案
1.【答案】D
【解析】在中,AB=5km,BC=10km,,根据余弦定理得,.故选D.
2.【答案】A
【解析】在中,,,所以,又所以由正弦定理,可得.故选A.
3.【答案】D
【解析】如图,若设出发点为A,AB=x,则有AC2=AB2+BC2-2AB·BC·cos30°,即()2=x2+32-2x·3cos30°,解得x=2或.故选D.
4.【答案】A
【解析】易知在中,海里,,
根据正弦定理得,解得(海里).故选A.
6.【答案】D
【解析】在中,,,,则,由正弦定理,可得.故选D.
7.【答案】A
【解析】如下图所示,在中,可得,,在中,由正弦定理,可得,所以.故选A.
9.【答案】
【解析】,解得.,又,所以为等边三角形,所以.
10.【答案】
【解析】如图,O,A分别为炮台底部和顶部,M,N为两艘船,假设由炮台顶部测得M船的俯角为,测得N船的俯角为,可求得m,m,又,所以可根据余弦定理求得.故两条船相距.
11.【答案】
【解析】根据题意画出示意图,如图,假设th后甲船行驶到D处,乙船行驶到C处,此时两船相距最近,则∠DBC=120°,BC=6t,BD=10-4t.在中,由余弦定理,得CD2=BD2+BC2-2BD·BCcos∠DBC=(10-4t)2+36t2-2(10-4t)6tcos120°=28t2-20t+100,所以当t=,即航行时间为h时,CD2最小,即甲、乙两船相距最近.
12.【答案】500
【解析】∵∠SAB=∠CAB?∠CAS=45°?30°=15°,∠SBA=∠ABC?∠SBC=45°?15°=30°,
∴在中,,∴(米).
∴BD=BS·sin75°=(米).故塔高BD为500米.
13.【答案】(1);(2),.
【解析】(1)由已知条件化简可得,即,
由余弦定理的推论,可得,.
(2),由正弦定理可得,
又,
在中,.
.
14.【答案】(1);(2).
【解析】(1)因为,,,所以,
由余弦定理可得.
15.【答案】C
【解析】设角,,所对的边分别为,,,由题意得 ①, ②,由①②得,,所以,解得.故选C.
16.【答案】D
【解析】在中,,即,即,在中,,即,即,故塔高为.故选D.
18.【答案】28
【解析】如图,在中,,由余弦定理得,∴(海里).故一小时后两船相距28海里.
19.【答案】没有
【解析】过点B作BD⊥AE交AE于D,由已知,AC=8,∠ABD=75°,∠CBD=60°,
在Rt中,AD=BD·tan∠ABD=BD·tan75°,
在Rt中,CD=BD·tan∠CBD=BD·tan60°,
所以AD-CD=BD(tan75°-tan60°)=AC=8,
所以,所以该军舰没有触礁的危险.
20.【答案】
【解析】因为,,所以,故,由正弦定理的变形可得,即,由可得,从而得,故,故,,故选A.
21.【答案】(1);(2).
【解析】(1)设,.
因为,,,,所以,,
所以,又,所以.
(2)设. 在中,,,,
由正弦定理可得,解得.
因为,所以为锐角,从而.
因此,
故的面积.
22.【答案】(1)21海里/小时;(2).
【解析】(1)依题意得,,,,.
在中由余弦定理可得,
所以,所以渔船甲的速度为海里/小时.
(2)在中,,,BC=42,,
由正弦定理,得,所以.
23.【答案】(1)海里/小时;(2)海里/小时;(3)存在,的取值范围为.
【解析】(1)设相遇时小艇的航行距离为海里,
则由余弦定理,可得
故当时,,此时,
即小艇以海里/小时的速度航行,相遇时小艇的航行距离最小.
(2)如图,设小艇与轮船在处相遇,
由题意可知,
化简得,
由于,所以,
所以当时,取得最小值,即小艇航行速度的最小值为海里/小时.
24.【答案】(1);(2).
【解析】(1)因为,即,
所以由正弦定理可得,
即,
又,所以,所以,
又,所以,即,又,所以.
(2)因为,所以由余弦定理可得,
因为,所以,即,
因为 所以,即,当且仅当时等号成立,
所以,所以的面积的最大值为.
25.【答案】C
【解析】由题可知,所以,由余弦定理可得,所以,因为,所以,故选C.
26.【答案】
【解析】根据题意,结合正弦定理可得,即,结合余弦定理可得,所以为锐角,且,所以,所以的面积.
27.【答案】
【解析】因为,所以,即,所以,则,则,因为为钝角,,所以,所以,,故.
29.【答案】(1);(2).
【解析】(1)由题设得,即.
由正弦定理得,故.
(2)由题设及(1)得,即.
所以,故.由题设得,即.
由余弦定理得,即,得.
故的周长为.
30.【答案】(1);(2).
【解析】(1)由题设及,可得,故.
上式两边同时平方,整理得,解得(舍去),.
(2)由可得,故,
又,所以.
由余弦定理及得,所以.
【名师点睛】解三角形问题是高考的高频考点,命题大多放在解答题的第一题,主要利用三角形的内角和定理,正余弦定理、三角形面积公式等知识进行求解.解题时要灵活利用三角形的边角关系进行“边转角”“角转边”,另外要注意三者之间的关系,这样的题目小而活,备受命题者的青睐.
知识
1.解三角形应用题的基本思想
解三角形应用题时,通常都要根据题意,从实际问题中抽象出一个或几个三角形,然后通过解三角形,得到实际问题的解,求解的关键是将实际问题转化为___________问题.
2.运用正弦定理、余弦定理解决实际问题的基本步骤
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
3.三角形面积公式
(1)三角形的高的公式:hA=bsinC=csinB,hB=csinA=asinC,hC=asinB=bsinA.
(2)三角形的面积公式:S=absinC,S=___________,S=___________.
知识参考答案:
1.解三角形
3.bcsinA casinB
重点
重点
从实际问题中抽象出一个或几个三角形,然后逐个解三角形,得到实际问题的解;利用三角形的面积公式解决与面积有关的问题
难点
测量距离、高度、角度问题中数学模型的建立,利用正弦定理、余弦定理求证简单的证明题
易错
解题时应由题意准确画出示意图,容易忽略图形的多种画法从而导致错误
测量距离问题
当的长度不可直接测量时,求,之间的距离有以下三种类型.
(1)如图1,A,B之间不可达也不可视
计算方法:测量,及角,由余弦定理可得.
(2)如图2,B,C与点A可视但不可达
计算方法:测量,角,角,则,由正弦定理可得.
(3)如图3,C,D与点A,B均可视不可达,
计算方法:测量,在中由正弦定理求,
在中由正弦定理求,在中由余弦定理求.
图1 图2 图3
如下图,为了测量河对岸A,B两点间的距离,在河的这边测得CD=km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为______________km.
【答案】
【解析】因为∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,所以∠DAC=60°,AC=DC=,
因为在中,∠DBC=45°,所以,所以BC=.
在中,由余弦定理得AB2=AC2+BC2-2AC·BC·cos45°=,
所以AB=,所以A,B两点间的距离为km.
【名师点睛】在解含有两个或两个以上的三角形的问题时,首先应根据条件应用正、余弦定理或三角形内角和定理在一个三角形中求解边和角,然后在此基础上求解另一个三角形,依此类推.首选哪一个三角形至关重要,原则是首选的三角形应与其他三角形有一定联系,且方便求解.
测量高度问题
当的高度不可直接测量时,求,之间的距离有以下三种类型.
(1)如图1,底部可达
计算方法:测量及角,则.
(2)如图2,底部不可达,但点与,共线
计算方法:测量,角,,由正弦定理求或,再解直角三角形求.
(3)如图3,底部不可达,且点与,不共线
计算方法:测量,在中由正弦定理求,再解直角三角形求.
图1 图2 图3
如下图,在地平面上有一旗杆OP,为了测量它的高度h,在地面上选一基线AB,测得AB=20 m,在A点处测得P点的仰角∠OAP=30°,在B点处测得P点的仰角∠OBP=45°,又测得∠AOB=60°,则旗杆的高度______________ m.(结果保留整数)
【答案】13
【解析】因为在Rt中,∠OAP=30°,OP=h,所以OA=.
在Rt中,∠OBP=45°,所以OB=h.
在中,AB=20,∠AOB=60°,由余弦定理得AB2=OA2+OB2-2×OA×OBcos60°,
即202=2+h2-2×h×h×,解得h2=≈176.4,所以h ≈13.
故旗杆的高度约为13 m.
【名师点睛】高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形或者在空间构造三棱锥,再依据条件利用正、余弦定理解其中的一个或者几个三角形,从而求出所需测量物体的高度.
测量角度问题
测量角度问题主要涉及海上、空中的追及与拦截,此时问题涉及方向角、方位角等概念,若是观察建筑物、山峰等,则会涉及俯角、仰角等概念.
如图,某船在A处看灯塔S在北偏东30°方向,它以每小时30海里的速度向正北方向航行,经过40分钟航行到B处,看灯塔S在北偏东75°方向,则此时该船到灯塔S的距离约为______________海里.(精确到0.01海里)
【答案】
【解析】由题图可知,在中,∠ABS=180°-75°=105°,∠BAS=30°,
所以∠ASB=45°,AB=30×=20(海里),由正弦定理,得,
故BS=,故该船到灯塔S的距离约为海里.
【名师点睛】解决此类问题的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.解题时应认真审题,结合图形去选择正、余弦定理,这是最重要的一步.
三角形的面积计算问题
在求三角形的面积时,若存在三角形边长平方和的情况,一般联想到用余弦定理解决;若存在边长乘积时,一般联想到用公式S=absinC=bcsinA=casinB解决.
在中,角A,B,C对应的三边分别是a,b,c,已知a=2,b=2,的面积S=,则
A. B.
C. D.或
【答案】D
【解析】由S=absinC=×2×2sinC=得sinC=,所以C=30°或150°.
①当C=30°时,由余弦定理得c2=a2+b2-2abcosC=(2)2+22-2×2×2cos30°=4,所以c=2.
②当C=150°时,由余弦定理得c2=a2+b2-2abcosC=(2)2+22-2×2×2cos150°=28,所以2.
综上,或.故选D.
【名师点睛】在解三角形面积的问题中,要注意三角形面积公式与余弦定理的结合.
三角形中边角关系恒等式的证明
在中,求证:.
【答案】证明见解析.
【解析】根据正弦定理,可设,显然 k ≠0,
所以,左边==右边,
所以.
【名师点睛】有关三角形的证明问题,主要涉及三角形的边和角的三角函数关系.从某种意义上看,这类问题就是有目标地对含边和角的式子进行化简的问题,所以解题思路与判断三角形的形状类似:将边化为角或者将角化为边.
基础训练
1.已知A,B两地的距离为5km,B,C两地的距离为10km,经测量可知,,则A,C两地的距离为
A.5km B.km
C.km D.km
2.如图,设,两点在河的两岸,一测量者在的同侧,在所在的河岸边选定的一点,测出的距离为,,后,就可以计算出,两点的距离为
A. B.
C. D.
3.某人向正东方向走了xkm后向右转了150°,然后沿新方向走了3km,结果离出发点恰好为km,那么x的值为
A. B.2
C.3 D.2或
4.如图,一艘轮船以每小时60海里的速度自A沿南偏东的方向直线航行,30分钟后到达B处,在C处有一座灯塔,轮船在A处观察灯塔,其方向是南偏东,在B处观察灯塔,其方向是北偏东,那么B,C间的距离是
A.海里 B.海里
C.海里 D.海里
5.若锐角三角形的面积为,且,,则
A. B.
C. D.
6.如图,巡航艇在海上以的速度沿南偏东的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东,航行到达C处,观测灯塔A的方向是北偏东,则巡航艇到达C处时,与灯塔A的距离是
A. B.
C. D.
7.一架直升飞机在600m的高空中,测得地面上一座塔的塔顶与塔底的俯角分别是和,则塔高为
A. B.
C. D.
8.一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8海里,则灯塔S在B处的
A.北偏东75° B.北偏东75°或东偏南75°
C.东偏南75° D.以上方位都不对
9.在中,若,则_____________.
10.江岸边有一炮台高,江中有两条船,船与炮台底部在同一水平面上,由炮台顶部测得两船的俯角分别为和,而且两条船与炮台底部连线成角,则两条船相距_____________.
11.甲船在岛B的正南A处,AB=10km,甲船以每小时4km的速度向正北航行,同时,乙船自B出发以每小时6km的速度向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间是_____________h.
12.如图所示,在山顶上有一座塔,在山底测得塔顶的仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得塔顶的仰角∠DSB=75°,则塔高BD=_____________米.
13.在中,角,,所对的边分别为,,,且.
(1)求角;
(2)若,求及的面积.
14.在中,角,,所对的边分别为,且.
(1)若,,求的值;
(2)若,且的面积,求和的值.
能力提升
15.已知的周长为20,面积为10,A=60°,则BC的长等于
A.5 B.6
C.7 D.8
16.如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C、D两处用测角仪测得塔顶部B处的仰角分别是和,如果C、D间的距离是,测角仪高为,则塔高为
A. B.
C. D.
17.在中,角,,的对边分别为,,,若,,且,则
A.2 B.3
C.4 D.5
18.两船同时从港出发,甲船以每小时20海里的速度向北偏东的方向航行,乙船以每小时12海里的速度向北偏西方向航行,一小时后两船相距_____________海里.
19.如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,则此舰____________触礁的危险.(填“有”或“没有”)
20.已知锐角三角形的内角,,的对边分别为,,,若,,则面积的取值范围是_____________.
21.在中,为边上一点,,,.
图1 图2
(1)如图1,若,求的大小;
(2)如图2,若,求的面积.
22.如图,渔船甲位于岛屿A的南偏西方向的B处,且与岛屿A相距18海里,渔船乙以15海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东的方向追赶渔船乙,刚好用2h追上,此时到达C处.
(1)求渔船甲的速度;
(2)求的值.
23.某港口要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的北偏西且与该港口相距海里的处,并正以海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以海里/小时的航行速度匀速行驶,经过小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在分钟内(含分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(3)是否存在,使得小艇以海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定的取值范围;若不存在,请说明理由.
24.在中,角,,的对边分别为,,,已知.
(1)求角的大小;
(2)若,求的面积的最大值.
真题练习
25.(2018新课标全国Ⅲ文理)的内角,,的对边分别为,,,若的面积为,则
A. B.
C. D.
26.(2018新课标全国Ⅰ文)的内角,,的对边分别为,,,已知,,则的面积为_____________.
27.(2018北京文)若的面积为,且为钝角,则_____________;的取值范围是_____________.
28.(2019浙江模拟)已知△ABC,AB=AC=4,BC=2.?点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是_____________,cos∠BDC=_____________.
29.(2019浙江模拟)的内角A,B,C的对边分别为a,b,c,已知的面积为.
(1)求sin Bsin C;
(2)若6cos Bcos C=1,a=3,求的周长.
30.(2019上海模拟)的内角A,B,C的对边分别为a,b,c,已知.
(1)求;
(2)若,的面积为,求.
参考答案
1.【答案】D
【解析】在中,AB=5km,BC=10km,,根据余弦定理得,.故选D.
2.【答案】A
【解析】在中,,,所以,又所以由正弦定理,可得.故选A.
3.【答案】D
【解析】如图,若设出发点为A,AB=x,则有AC2=AB2+BC2-2AB·BC·cos30°,即()2=x2+32-2x·3cos30°,解得x=2或.故选D.
4.【答案】A
【解析】易知在中,海里,,
根据正弦定理得,解得(海里).故选A.
6.【答案】D
【解析】在中,,,,则,由正弦定理,可得.故选D.
7.【答案】A
【解析】如下图所示,在中,可得,,在中,由正弦定理,可得,所以.故选A.
9.【答案】
【解析】,解得.,又,所以为等边三角形,所以.
10.【答案】
【解析】如图,O,A分别为炮台底部和顶部,M,N为两艘船,假设由炮台顶部测得M船的俯角为,测得N船的俯角为,可求得m,m,又,所以可根据余弦定理求得.故两条船相距.
11.【答案】
【解析】根据题意画出示意图,如图,假设th后甲船行驶到D处,乙船行驶到C处,此时两船相距最近,则∠DBC=120°,BC=6t,BD=10-4t.在中,由余弦定理,得CD2=BD2+BC2-2BD·BCcos∠DBC=(10-4t)2+36t2-2(10-4t)6tcos120°=28t2-20t+100,所以当t=,即航行时间为h时,CD2最小,即甲、乙两船相距最近.
12.【答案】500
【解析】∵∠SAB=∠CAB?∠CAS=45°?30°=15°,∠SBA=∠ABC?∠SBC=45°?15°=30°,
∴在中,,∴(米).
∴BD=BS·sin75°=(米).故塔高BD为500米.
13.【答案】(1);(2),.
【解析】(1)由已知条件化简可得,即,
由余弦定理的推论,可得,.
(2),由正弦定理可得,
又,
在中,.
.
14.【答案】(1);(2).
【解析】(1)因为,,,所以,
由余弦定理可得.
15.【答案】C
【解析】设角,,所对的边分别为,,,由题意得 ①, ②,由①②得,,所以,解得.故选C.
16.【答案】D
【解析】在中,,即,即,在中,,即,即,故塔高为.故选D.
18.【答案】28
【解析】如图,在中,,由余弦定理得,∴(海里).故一小时后两船相距28海里.
19.【答案】没有
【解析】过点B作BD⊥AE交AE于D,由已知,AC=8,∠ABD=75°,∠CBD=60°,
在Rt中,AD=BD·tan∠ABD=BD·tan75°,
在Rt中,CD=BD·tan∠CBD=BD·tan60°,
所以AD-CD=BD(tan75°-tan60°)=AC=8,
所以,所以该军舰没有触礁的危险.
20.【答案】
【解析】因为,,所以,故,由正弦定理的变形可得,即,由可得,从而得,故,故,,故选A.
21.【答案】(1);(2).
【解析】(1)设,.
因为,,,,所以,,
所以,又,所以.
(2)设. 在中,,,,
由正弦定理可得,解得.
因为,所以为锐角,从而.
因此,
故的面积.
22.【答案】(1)21海里/小时;(2).
【解析】(1)依题意得,,,,.
在中由余弦定理可得,
所以,所以渔船甲的速度为海里/小时.
(2)在中,,,BC=42,,
由正弦定理,得,所以.
23.【答案】(1)海里/小时;(2)海里/小时;(3)存在,的取值范围为.
【解析】(1)设相遇时小艇的航行距离为海里,
则由余弦定理,可得
故当时,,此时,
即小艇以海里/小时的速度航行,相遇时小艇的航行距离最小.
(2)如图,设小艇与轮船在处相遇,
由题意可知,
化简得,
由于,所以,
所以当时,取得最小值,即小艇航行速度的最小值为海里/小时.
24.【答案】(1);(2).
【解析】(1)因为,即,
所以由正弦定理可得,
即,
又,所以,所以,
又,所以,即,又,所以.
(2)因为,所以由余弦定理可得,
因为,所以,即,
因为 所以,即,当且仅当时等号成立,
所以,所以的面积的最大值为.
25.【答案】C
【解析】由题可知,所以,由余弦定理可得,所以,因为,所以,故选C.
26.【答案】
【解析】根据题意,结合正弦定理可得,即,结合余弦定理可得,所以为锐角,且,所以,所以的面积.
27.【答案】
【解析】因为,所以,即,所以,则,则,因为为钝角,,所以,所以,,故.
29.【答案】(1);(2).
【解析】(1)由题设得,即.
由正弦定理得,故.
(2)由题设及(1)得,即.
所以,故.由题设得,即.
由余弦定理得,即,得.
故的周长为.
30.【答案】(1);(2).
【解析】(1)由题设及,可得,故.
上式两边同时平方,整理得,解得(舍去),.
(2)由可得,故,
又,所以.
由余弦定理及得,所以.
【名师点睛】解三角形问题是高考的高频考点,命题大多放在解答题的第一题,主要利用三角形的内角和定理,正余弦定理、三角形面积公式等知识进行求解.解题时要灵活利用三角形的边角关系进行“边转角”“角转边”,另外要注意三者之间的关系,这样的题目小而活,备受命题者的青睐.
