第三章 位置与坐标单元测试卷B(含答案)
文档属性
| 名称 | 第三章 位置与坐标单元测试卷B(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-08 21:53:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2019—2020学年北师大版七年级上册第三章《位置与坐标》单元测试试卷B
一、选择题(共12小题;共36分)
1. 在平面直角坐标系中,若点 在第四象限内,则点 所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 若将点 向左平移 个单位,再向下平移 个单位得到点 ,则点 的坐标为
A. B. C. D.
3. 下列说法正确地有
(1)点 一定在第四象限;(2)坐标轴上的点不属于任一象限;(3)若点 在坐标轴的角平分线上,则 ;(4)直角坐标系中,在 轴上且到原点的距离为 的点的坐标是 .
A. 个 B. 个 C. 个 D. 个
4. 如图,在平面直角坐标系中 ,,,则 的面积为
A. B. C. D.
5. 点 关于 轴的对称点的坐标是
A. B. C. D.
6. 如图,在平面直角坐标系中, 的三个顶点的坐标分别为 ,,.将 沿 轴翻折得到 ,则点 的坐标为
A. B. C. D.
7. 小李在平面直角坐标系中画了一张示意图,如图,分别标出了学校、工厂、体育馆、百货商店的大致位置.已知从学校向东走 米,再向北走 米 到达工厂.如果张大爷从工厂向南走 米,再向西走 米,再向南走 米,再向东走 米,最终到达的地点是
A. 学校 B. 工厂 C. 体育馆 D. 百货商店
8. 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用 表示,小军的位置用 表示,那么你的位置可以表示成
A. B. C. D.
9. 在平面直角坐标系 中,若点 的坐标为 ,点 的坐标为 ,则 的面积为
A. B. C. D.
10. 已知点 ,,点 在 轴上,三角形 的面积为 ,则点 的坐标为
A. B.
C. 或 D. 或
11. 在平面直角坐标系 中,对于任意三点 ,, 的“矩面积”,给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.例如:三点坐标分别为 ,,,则“水平底”,“铅垂高”,“矩面积”.若 ,, 三点的“矩面积”为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
12. 如图所示,已知校门的坐标是 ,下列对于实验楼位置的叙述正确的有
①实验楼的坐标是
②实验楼的坐标是
③实验楼的坐标为
④实验楼在校门的东北方向上,距校门
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共24分)
13. 已知点 关于 轴的对称点为 ,则 ?.
14. 如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标为 和 ,那么第一架轰炸机 的平面坐标是 ?.
15. 在直角坐标系中一点 ,点 关于 轴的对称点 的坐标为 ?.
16. 若第二象限内的点 满足 ,,则点 的坐标是 ?.
17. 如图,直角坐标系中, 的顶点都在格点上,其中点 的坐标为 ,则 的面积为 ?.
18. (1)已知 ,,,则 的面积是 ?;
(2)若 , 的坐标不变, 的面积为 ,点 的横坐标为 ,那么点 的坐标为 ?.
三、解答题(共7小题;共60分)
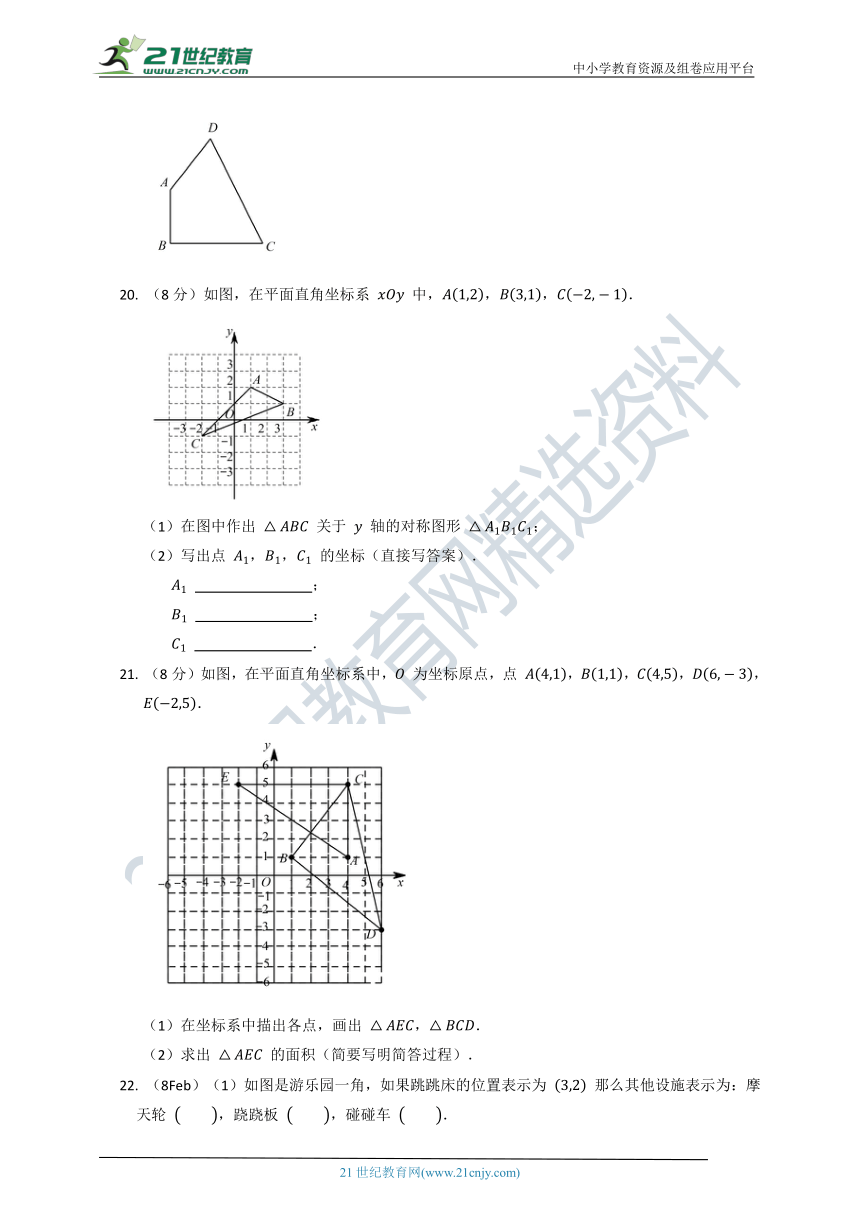
19. (8分)有一块形状为四边形的钢板,量得它的各边长度为 ,,,,.求这块钢板的面积.
20. (8分)如图,在平面直角坐标系 中,,,.
(1)在图中作出 关于 轴的对称图形 ;
(2)写出点 ,, 的坐标(直接写答案).
?;
?;
?.
21. (8分)如图,在平面直角坐标系中, 为坐标原点,点 ,,,,.
(1)在坐标系中描出各点,画出 ,.
(2)求出 的面积(简要写明简答过程).
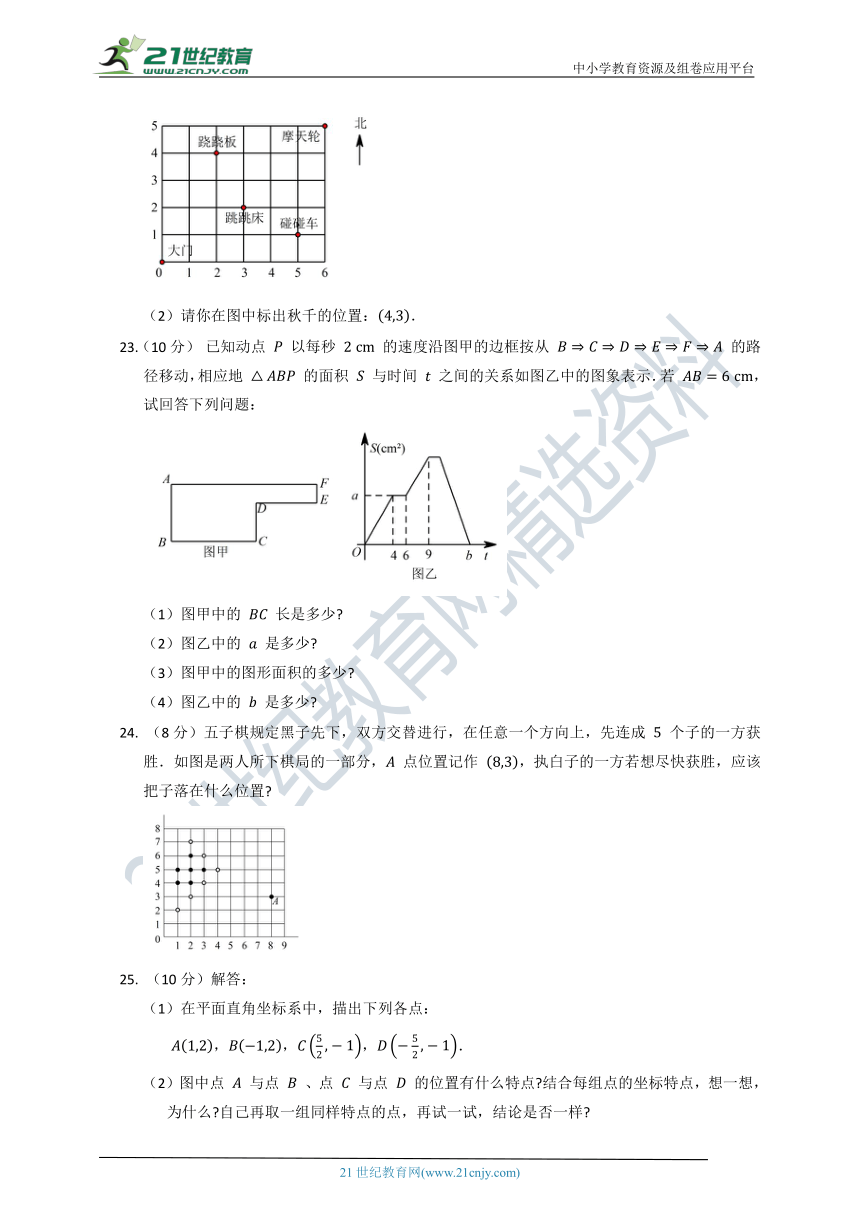
22. (8Feb)(1)如图是游乐园一角,如果跳跳床的位置表示为 那么其他设施表示为:摩天轮 ,跷跷板 ,碰碰车 .
(2)请你在图中标出秋千的位置:.
23.(10分) 已知动点 以每秒 的速度沿图甲的边框按从 的路径移动,相应地 的面积 与时间 之间的关系如图乙中的图象表示.若 ,试回答下列问题:
(1)图甲中的 长是多少?
(2)图乙中的 是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的 是多少?
24. (8分)五子棋规定黑子先下,双方交替进行,在任意一个方向上,先连成 个子的一方获胜.如图是两人所下棋局的一部分, 点位置记作 ,执白子的一方若想尽快获胜,应该把子落在什么位置?
25. (10分)解答:
(1)在平面直角坐标系中,描出下列各点:
,,,.
(2)图中点 与点 、点 与点 的位置有什么特点?结合每组点的坐标特点,想一想,为什么?自己再取一组同样特点的点,再试一试,结论是否一样?
(3)写出点 关于 轴对称的点的坐标: ? .
答案
第一部分
1. A
2. C 【解析】本题考查坐标与图形变化——平移. 点 向左平移 个单位,再向下平移 个单位得到点 , 点 的横坐标为 ,纵坐标为 . 点 的坐标为 .
3. A
4. A
5. B
6. B
7. D
8. D
9. D
10. C
11. C
12. B
第二部分
13.
14.
15.
16.
17.
18. (1),(2)或
第三部分
19. 连接 ,
在 中,,
在 中,,,
则 ,
故可得 为直角三角形,
20. (1) 所作图形如下所示:
??????(2) ;;
【解析】,, 的坐标分别为:,,.
21. (1) 如图所示:
??????(2) 取 为底,则 为 , 边上高 ,
所以 .
22. (1) ;;
??????(2) 秋千的位置,如图所示:
23. (1) 动点 在 上运动时,对应的时间为 到 秒,易得:;
故图甲中的 长是 .
??????(2) 由(1)可得,,则:;
图乙中的 是 .
??????(3) 由图可得:,,
则 ,又由 ,
则甲图的面积为 ,
图甲中的图形面积的 .
??????(4) 根据题意,动点 共运动了 ,
其速度是 ,则 秒,
图乙中的 是 秒.
24. 或
25. (1) 如图即为所求.
??????(2) 点 与点 关于 轴对称,点 与点 关于 轴对称.
如果两个点的纵坐标相同,橫坐标互为相反数,这两个关于 轴对称,即点 与点 关于 轴对称.
??????(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2019—2020学年北师大版七年级上册第三章《位置与坐标》单元测试试卷B
一、选择题(共12小题;共36分)
1. 在平面直角坐标系中,若点 在第四象限内,则点 所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 若将点 向左平移 个单位,再向下平移 个单位得到点 ,则点 的坐标为
A. B. C. D.
3. 下列说法正确地有
(1)点 一定在第四象限;(2)坐标轴上的点不属于任一象限;(3)若点 在坐标轴的角平分线上,则 ;(4)直角坐标系中,在 轴上且到原点的距离为 的点的坐标是 .
A. 个 B. 个 C. 个 D. 个
4. 如图,在平面直角坐标系中 ,,,则 的面积为
A. B. C. D.
5. 点 关于 轴的对称点的坐标是
A. B. C. D.
6. 如图,在平面直角坐标系中, 的三个顶点的坐标分别为 ,,.将 沿 轴翻折得到 ,则点 的坐标为
A. B. C. D.
7. 小李在平面直角坐标系中画了一张示意图,如图,分别标出了学校、工厂、体育馆、百货商店的大致位置.已知从学校向东走 米,再向北走 米 到达工厂.如果张大爷从工厂向南走 米,再向西走 米,再向南走 米,再向东走 米,最终到达的地点是
A. 学校 B. 工厂 C. 体育馆 D. 百货商店
8. 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用 表示,小军的位置用 表示,那么你的位置可以表示成
A. B. C. D.
9. 在平面直角坐标系 中,若点 的坐标为 ,点 的坐标为 ,则 的面积为
A. B. C. D.
10. 已知点 ,,点 在 轴上,三角形 的面积为 ,则点 的坐标为
A. B.
C. 或 D. 或
11. 在平面直角坐标系 中,对于任意三点 ,, 的“矩面积”,给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.例如:三点坐标分别为 ,,,则“水平底”,“铅垂高”,“矩面积”.若 ,, 三点的“矩面积”为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
12. 如图所示,已知校门的坐标是 ,下列对于实验楼位置的叙述正确的有
①实验楼的坐标是
②实验楼的坐标是
③实验楼的坐标为
④实验楼在校门的东北方向上,距校门
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共24分)
13. 已知点 关于 轴的对称点为 ,则 ?.
14. 如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标为 和 ,那么第一架轰炸机 的平面坐标是 ?.
15. 在直角坐标系中一点 ,点 关于 轴的对称点 的坐标为 ?.
16. 若第二象限内的点 满足 ,,则点 的坐标是 ?.
17. 如图,直角坐标系中, 的顶点都在格点上,其中点 的坐标为 ,则 的面积为 ?.
18. (1)已知 ,,,则 的面积是 ?;
(2)若 , 的坐标不变, 的面积为 ,点 的横坐标为 ,那么点 的坐标为 ?.
三、解答题(共7小题;共60分)
19. (8分)有一块形状为四边形的钢板,量得它的各边长度为 ,,,,.求这块钢板的面积.
20. (8分)如图,在平面直角坐标系 中,,,.
(1)在图中作出 关于 轴的对称图形 ;
(2)写出点 ,, 的坐标(直接写答案).
?;
?;
?.
21. (8分)如图,在平面直角坐标系中, 为坐标原点,点 ,,,,.
(1)在坐标系中描出各点,画出 ,.
(2)求出 的面积(简要写明简答过程).
22. (8Feb)(1)如图是游乐园一角,如果跳跳床的位置表示为 那么其他设施表示为:摩天轮 ,跷跷板 ,碰碰车 .
(2)请你在图中标出秋千的位置:.
23.(10分) 已知动点 以每秒 的速度沿图甲的边框按从 的路径移动,相应地 的面积 与时间 之间的关系如图乙中的图象表示.若 ,试回答下列问题:
(1)图甲中的 长是多少?
(2)图乙中的 是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的 是多少?
24. (8分)五子棋规定黑子先下,双方交替进行,在任意一个方向上,先连成 个子的一方获胜.如图是两人所下棋局的一部分, 点位置记作 ,执白子的一方若想尽快获胜,应该把子落在什么位置?
25. (10分)解答:
(1)在平面直角坐标系中,描出下列各点:
,,,.
(2)图中点 与点 、点 与点 的位置有什么特点?结合每组点的坐标特点,想一想,为什么?自己再取一组同样特点的点,再试一试,结论是否一样?
(3)写出点 关于 轴对称的点的坐标: ? .
答案
第一部分
1. A
2. C 【解析】本题考查坐标与图形变化——平移. 点 向左平移 个单位,再向下平移 个单位得到点 , 点 的横坐标为 ,纵坐标为 . 点 的坐标为 .
3. A
4. A
5. B
6. B
7. D
8. D
9. D
10. C
11. C
12. B
第二部分
13.
14.
15.
16.
17.
18. (1),(2)或
第三部分
19. 连接 ,
在 中,,
在 中,,,
则 ,
故可得 为直角三角形,
20. (1) 所作图形如下所示:
??????(2) ;;
【解析】,, 的坐标分别为:,,.
21. (1) 如图所示:
??????(2) 取 为底,则 为 , 边上高 ,
所以 .
22. (1) ;;
??????(2) 秋千的位置,如图所示:
23. (1) 动点 在 上运动时,对应的时间为 到 秒,易得:;
故图甲中的 长是 .
??????(2) 由(1)可得,,则:;
图乙中的 是 .
??????(3) 由图可得:,,
则 ,又由 ,
则甲图的面积为 ,
图甲中的图形面积的 .
??????(4) 根据题意,动点 共运动了 ,
其速度是 ,则 秒,
图乙中的 是 秒.
24. 或
25. (1) 如图即为所求.
??????(2) 点 与点 关于 轴对称,点 与点 关于 轴对称.
如果两个点的纵坐标相同,橫坐标互为相反数,这两个关于 轴对称,即点 与点 关于 轴对称.
??????(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
