人教版九年级数学下册第二十八章 锐角三角函数28.1锐角三角函数课件4课时(107张PPT)
文档属性
| 名称 | 人教版九年级数学下册第二十八章 锐角三角函数28.1锐角三角函数课件4课时(107张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-09 07:19:47 | ||
图片预览









文档简介
课件107张PPT。28.1锐角三角函数第一课时第二课时第三课时第四课时人教版 数学 九年级 下册 正弦第一课时返回鞋跟多高合适 美国人体工程研究学人员调查发现,
当高跟鞋的鞋底与地面的夹角为11°左
右时,人脚的感觉最舒适,假设某成年人前脚掌到
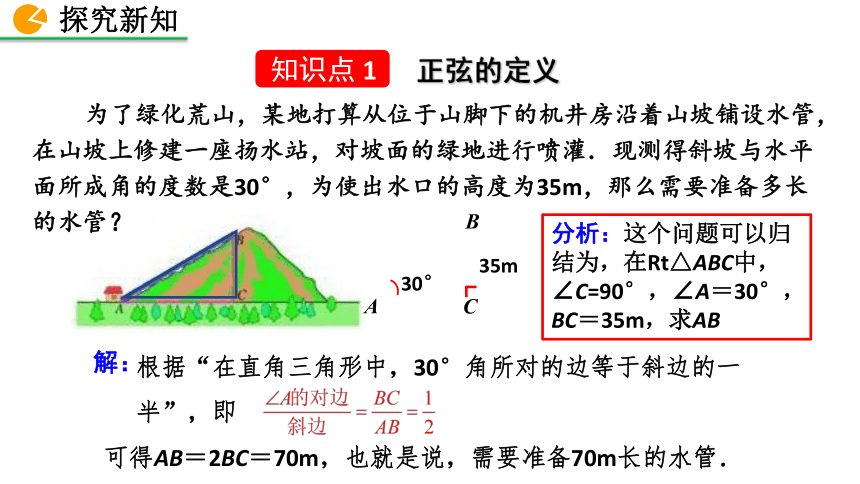
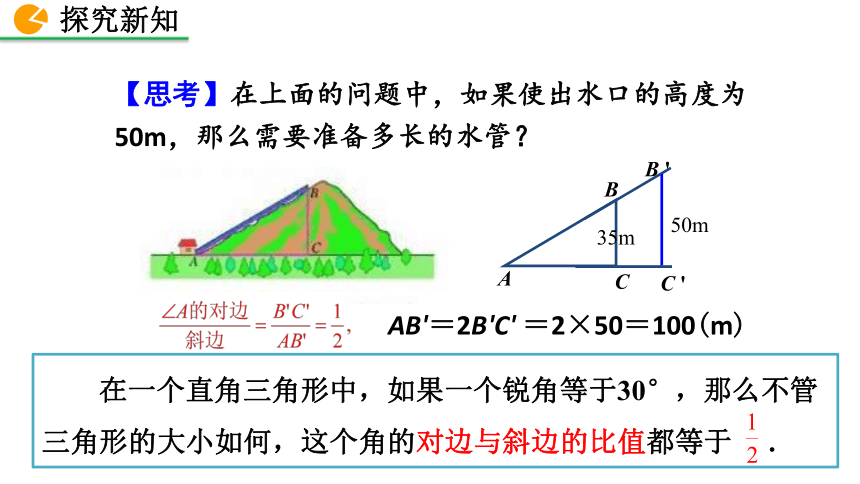
脚后跟长为15厘米,请问鞋跟在几厘米高度为最佳?11?1. 经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实. 2. 理解锐角正弦的概念,掌握正弦的表示方法.素养目标3. 会根据直角三角形的边长求一个锐角的正弦值,并且能利用正弦求直角三角形的边长. 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?分析:这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管.正弦的定义 解:【思考】在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?ABC50m35mB 'C 'AB'=2B'C' =2×50=100(m) 在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 . 在Rt△ABC中,∠C=90°,由于∠A=45°,所以Rt△ABC是等腰直角三角形,由勾股定理得:因此 在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 . 如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,
你能得出什么结论?
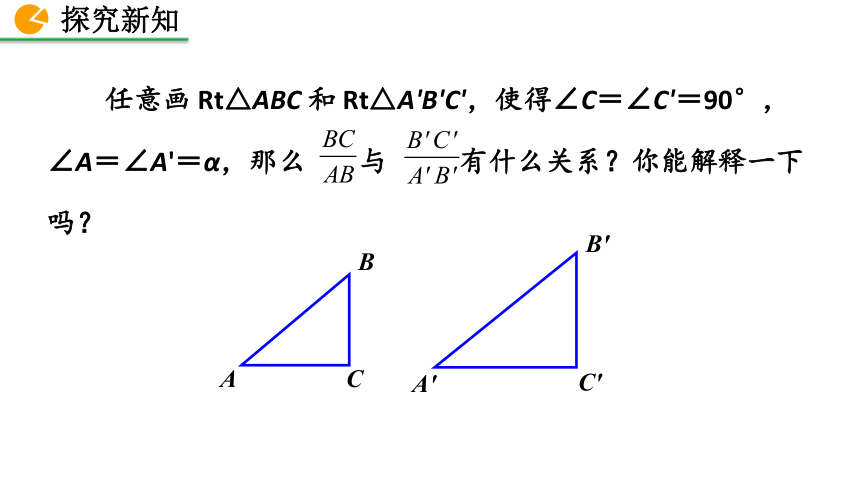
归纳总结 综上可知,在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于 ,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于 ,也是一个固定值.【思考】一般地,当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?ABCA'B'C' 任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?因为∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'. 因此 在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比都是一个固定值. 如图,在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即例如,当∠A=30°时,我们有当∠A=45°时,我们有归纳:注意sinA是一个完整的符号,它表示∠A的正弦,记号里习惯省去角的符号“∠”;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
sinA不表示“sin”乘以“A”. 例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解:(1)在Rt△ABC中,因此(2)在Rt△ABC中,因此利用正弦的定义求有关角的正弦值1.判断对错: (1) ( )
(2) ( )
(3)sin A=0.6m ( )
(4)sin B=0.8 ( )
√√××sin A是一个比值(注意比的顺序),无单位;2)如图②, ( ) ×1) 如图① 图① 图② 2. 在 Rt△ABC中,锐角 A 的对边和斜边同时扩大 100 倍,sinA 的值 ( )
A. 扩大100倍 B. 缩小
C. 不变 D. 不能确定C 例2 如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.解:如图,设点 A (3,0),连接 PA .A (3,0)在Rt△APO中,由勾股定理得因此α在平面直角坐标系内求锐角的正弦值 方法点拨 结合平面直角坐标系求某角的正弦函数值,一般过已知点向 x 轴或 y 轴作垂线,构造直角三角形,再结合勾股定理求解.3.在平面直角坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____345 例3 如图,在 Rt△ABC 中,∠C=90°, ,
BC = 3,求 sinB 及 Rt△ABC 的面积.
提示:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长. 然后再利用勾股定理,求出 AC 的长度,进而求出 sinB 及 Rt△ABC 的面积.利用正弦求直角三角形的边长∴ AB = 3BC =3×3=9.∴∴∴解:∵在 Rt△ABC 中,
∴ 在 Rt△ABC 中,∠C = 90°,sinA = k,
sinB = h,AB = c,则BC = ck,AC = ch. 在 Rt△ABC 中,∠C = 90°,sinA = k,
sinB = h,BC=a,则归纳:,.84.如图:在Rt△ABC中,∠C=90°,AB=10,
, BC的长是 . 例4 在 △ABC 中,∠C=90°,AC=24cm, ,求这个三角形的周长.解:设BC=7x,则AB=25x,在 Rt△ABC中,由勾股定理得即 24x = 24cm,解得 x = 1 cm.故 BC = 7x = 7 cm,AB = 25x = 25 cm.所以 △ABC 的周长为 AB+BC+AC = 7+24+25 = 56 (cm).利用方程和正弦求直角三角形中线段 5.如图,在Rt△ABC中,∠C=90°, , AC=12.
求sinB的值.513解:在Rt △ABC中,
设AB=13x,BC=5x,
由勾股定理得:(5x)2+122=(13x)2解得x=1.所以AB=13,BC=5因此1.(2018?柳州)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.巩固练习A2.(2018?德州)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是_______.巩固练习1. 如图,已知点 P 的坐标是 (a,b),则 sinα 等于( )A. B.
C. D.D2. 在直角三角形 ABC 中,若三边长都扩大 2 倍,则
锐角 A 的正弦值 ( )
A. 扩大 2 倍 B.不变
C. 缩小 D. 无法确定BDA. 4 B. 6 C. 8 D. 1023. 在Rt△ABC中,∠C=90°, ,BC=6,则 AB
的长为 ( )4. 在△ABC中,∠C=90°,如果 ,AB=6,
那么BC=_____.5. 如图,在正方形网格中有 △ABC,则 sin∠ABC 的值为 .解析:∵ , , ,∴∴ AB 2 = BC 2+AC 2,∴ ∠ACB=90°, 如图,在 △ABC中, AB= BC = 5, ,求 △ABC 的面积.D解:作BD⊥AC于点D, ∴又∵ △ABC 为等腰三角形,BD⊥AC,∴ AC=2AD=6,
∴S△ABC=AC×BD÷2=12.
∵ ,求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB. sinB可以由哪两条线段之比得到?若AC=5,CD=3,求sinB的值.解: ∵∠B =∠ACD ∴sinB = sin∠ACD在Rt△ACD中, ∴ ∴ 正弦函数正弦函数的概念正弦函数的应用已知边长求正弦值已知正弦值求边长余弦和正切第二课时返回 如图,在Rt△ABC中,∠C=90°.当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?2. 能灵活运用锐角三角函数进行相关运算.1. 通过类比正弦函数,理解余弦函数、正切函数的定义,进而得到锐角三角函数的概念 .素养目标3. 通过锐角三角函数的学习,培养学生类比学习的能力. 如图, △ABC 和 △DEF 都是直角三角形,
其中∠A =∠D,∠C =∠F = 90°,则
成立吗?为什么?余弦的定义我们来试着证明前面的问题:从而 sinB = sinE,因此 在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关. 如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即归纳:
归纳总结 从上述探究和证明过程,可以得到互余两角的三角函数之间的关系:
对于任意锐角α,有 cos α = sin (90°-α),
或sin α = cos (90°-α). 1. sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2. sinA、 cosA是一个比值(数值).
3. sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.如图:在Rt △ABC中,∠C=90°,正弦余弦注意:1.Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为( )A. B. C. D. A2. Rt△ABC中,∠C=90°,如果AC=4,BC=3,
那么cosB的值为_______ 如图, △ABC 和 △DEF 都是直角三角形,
其中∠A =∠D,∠C =∠F = 90°,则
成立吗?为什么?正切的定义证明:∵∠C=∠F=90°,
∠A=∠D,
∴Rt△ABC ∽ Rt△DEF∴即如图:在Rt △ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的 正切,记作 tanA. 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值. 1.如果两个角互余,那么这两个角的正切值有什么关系?【想一想】2.锐角A的正切值可以等于1吗?为什么?可以大于1吗?3.在Rt?ABC中,∠C=90°,如果
那么tanB的值为( )A. B. C. D. D4. 在Rt?ABC中,∠C=90°,如果
那么tanA的值为_______.锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.sin A= cos A= tan A= 脑中有“图”,心中有“式”锐角三角函数的定义 例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.解:由勾股定理得因此已知直角三角形两边求锐角三角函数的值 方法点拨 已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值. 5.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是( )6.如图:P是∠ α的边OA上一点,且P点的坐标为(3,4),则cos α
______,tan α = ________.B又已知一边及一锐角三角函数值求函数值 例2 如图,在 Rt△ABC中,∠C = 90°,BC = 6,
,求 cosA、tanB 的值.∴解:∵在Rt△ABC中,
∴解:∵在 Rt△ABC中,∴∴∴7. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8, , 求sinA,cosB 的值.1.(2018?广州)如图,旗杆高AB=8m,某一时刻,旗杆影子
长BC=16m,则tanC=______.巩固练习2. (2018?贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D. B1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为:
.==∠A +∠B = 90° 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.解: ∵ ∠ACB=∠ADC =90°,∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,∴∠B = ∠ACD,∴ 如图,在△ABC中,AB=AC=4,BC=6.
求cosB 及 tanB 的值.解:过点 A 作 AD⊥BC 于 D.∵ AB = AC, ∴ BD = CD = 3,在 Rt△ABD 中,D提示:求锐角的三角函数值问题,当图形中没有直角三角形时,可用恰当的方法构造直角三角形.∴∴ 余弦函数和
正切函数余弦正切性质30°、45°、60°角的三角函数值第三课时返回 还记得我们推导正弦关系的时候所得到的结论吗?即 , ,你还能推导出sin60°的值及
30°、45°、60°角的其它三角函数值吗?1. 理解特殊角的三角函数值的由来.
3. 熟记三个特殊锐角的三角函数值,并能准确地加以运用,根据一个特殊角的三角函数值说出这个角.素养目标2. 运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.
设30°所对的直角边长为a,那么斜边长为2a,另一条直角边长=30°60°45°45°特殊角(30°、45°、60°)的三角函数值
∴设两条直角边长为a,则斜边长=∴∴30°、45°、60°角的正弦值、余弦值和正切值如下表:三角函数例1 求下列各式的值:
(1)cos260°+sin260° (2)解: (1) cos260°+sin260°= 1(2)=0特殊角的三角函数值的运算提示:sin260°表示(sin60°)2 方法点拨 含特殊角三角函数值的计算注意事项:
(1)熟记特殊角的锐角三角函数值是关键;
(2)注意运算顺序和法则;
(3)注意特殊角三角函数值的准确代入. 1.计算:
(1) sin30°+ cos45°;解:(1)原式 (2) sin230°+ cos230°-tan45°.(2)原式=1-1=0解:在 Rt△ABC中 ∴ ∠A = 45°.∵利用三角函数值求特殊角例2 (1) 如图,在Rt△ABC中,∠C = 90°, ,
,求 ∠A 的度数;解:在 Rt△ABO中 ∴ α = 60°. (2) 如图,AO 是圆锥的高,OB 是底面半径, ,求 α 的度数.∵2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.解: 由勾股定理∴ ∠ A=30°∠B = 90°- ∠ A = 90°-30°= 60°∴ 例3 已知 △ABC 中的 ∠A 与 ∠B 满足 (1-tanA)2 +|sinB- |=0,试判断 △ABC 的形状. ∴ tanA=1, ,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.特殊角的三角函数值的应用解:∵ (1-tanA)2 + | sinB- |=0,∴ ∠A=45°,∠B=60°,
3. 已知:
求∠A,∠B的度数。解:即∴∴∵巩固练习A1.(2018?大庆)2cos60°=( )
A.1 B. C. D.2.(2019?大庆)计算:(2019-π)0 + -sin60°
解:原式=1+ -1 -=1.下列各式中不正确的是( )
A. B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
2.计算2sin30°-2cos60°+tan45°的结果是( )
A.2 B. C.-1 D.1 BDsin260°+cos260°=13.求满足下列条件的锐角 α .(1) 2sinα - = 0; (2) tanα-1 = 0. ∴ ∠α = 60°.(2) tanα =1, 解:(1) , ∴ ∠α = 45°. 4.在△ABC中,∠A、∠B都是锐角,且 ,
,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定 B5. 在 △ABC 中,若 ,
则∠C = . 120° 6. 求下列各式的值:
(1) 1-2 sin30°cos30°;
(2) 3tan30°-tan45°+2sin60°;
(3) ;
(4)答案:(1)(2)(3) 2(4) 已知 α 为锐角,且 tanα 是方程 x2 + 2x -3 = 0
的一个根,求 2 sin2α + cos2α - tan (α+15°)的值.解:解方程 x2 + 2x - 3 = 0,得 x1 = 1,x2 = -3.
∵ tanα >0,∴ tanα =1,∴ α = 45°.
∴ 2 sin2α + cos2α - tan (α+15°)
= 2 sin245°+cos245°- tan60° 如图,在△ABC中,AD⊥BC,M为AB的中点,∠B=30°,
. 求tan∠BCM.
E解:过点M作ME⊥BC于点E∴CD=AD,又∵M是AB的中点∴BE=DE,AD=2ME.又∵∠B=30°,∵AD⊥BC,∴∴∴30°、45°、60°角的三角函数值通过三角函数值求角度特殊角的三角函数值用计算器求锐角三角函数值
第四课时返回 1填写下表: 前面我们学习了特殊角30°,45°,60°的三角函数值,一些非特殊角(如17°,56°,89°等)的三角函数值又怎么求呢?这一节课我们就学习借助计算器来完成这个任务.1. 会使用科学计算器求锐角的三角函数值.
2. 会根据锐角的三角函数值,借助科学计算器求锐角的大小.素养目标3. 熟练运用计算器解决锐角三角函数中的问题.例如 (1) 用计算器求sin18°的值;第二步:输入角度值18;屏幕显示结果 sin18°= 0.309 016 994.利用计算器求三角函数值、角的度数(2) 用计算器求 tan30°36′ 的值;解:方法①:第二步:输入角度值30.6 (因为30°36′ = 30.6°);屏幕显示答案:0.591 398 351.屏幕显示答案:0.591 398 351.方法②:(3) 已知 sinA = 0.501 8,用计算器求锐角∠A的度数.第二步:输入函数值0. 501 8; 屏幕显示答案: 30.119 158 67°(按实际需要进行
精确).解: 1. 用计算器求下列各式的值(精确到0.0001):
(1) sin47°; (2) sin12°30′;
(3) cos25°18′;(4) sin18°+cos55°-tan59°.答案:(1) 0.7314 (2) 0.2164 (3) 0.9041(4) -0.78172. 已知下列锐角三角函数值,用计算器求锐角 ∠A,
∠B的度数 (结果精确到0.1°):
(1) sinA=0.7,sinB=0.01;
(2) cosA=0.15,cosB=0.8;
(3) tanA=2.4,tanB=0.5.答案:(1) ∠A ≈ 44.4°;∠B ≈ 0.6°.
(2) ∠A ≈ 81.4°;∠B ≈ 36.9°.
(3) ∠A ≈ 67.4°;∠B ≈ 26.6°.(1)通过计算 (可用计算器),比较下列各组数的大小,并提出你的猜想:
① sin30°____2sin15°cos15°;
② sin38°____2sin19°cos19°;
③ sin45°____2sin22.5°cos22.5°;
④ sin60°____2sin30°cos30°;
⑤ sin84°____2sin42°cos42°.
猜想:已知0°<α<45°,则sin2α___2sinαcosα.=利用计算器探索三角函数的性质=====(2) 如图,在△ABC中,AB=AC=1,∠BAC=2α,
请利用面积方法验证 (1) 中的结论.证明:∵ S△ABC = AB · sin2α · AC = sin2α,
S△ABC = ×2ABsinα · ACcosα = sinα · cosα,
∴sin2α=2sinαcosα.2α(1)sin35°= ,cos35°= ,
sin235°= ,cos235°= ;
猜想:
已知0°<α<90°,则 sin2α + cos2α = .0.34200.57350.93970.11700.88300.8192 0.32900.67103.利用计算器求值,并提出你的猜想:1(2)sin20°= , cos20°= ,sin220°= , cos220°= ; 4. 已知:sin254°+ cos2α =1,则锐角 α = . 54° 5. 用计算器比较大小:20sin87° tan87°.> sin20° cos20°,
sin220° cos220°;
sin35° cos35°.< < < (2018?淄博)一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是( )
A. B.
C. D.巩固练习A1. 下列式子中,不成立的是( )
A.sin35°= cos55°
B.sin25°+ sin40°= sin65°
C. cos47°= sin43°
D.sin218°+ cos218°=1B2. 用计算器求sin24°37′18″的值,以下按键顺序正确的是 ( )
A.
B.
C.
D. A(1) sin40°≈ (精确到0.0001);
(2) tan63°27′≈ (精确到 0.0001);
(3) cos18°59′27″≈ (精确到 0.0001);
(4) 若sinα = 0.5225,则 α ≈ (精确到 0.1°);
(5) 若cosα = 0.3145,则 α ≈ (精确到 0.1°).0.64282.001331.5°3. 利用计算器求值:71.7°0.9452 如图,在 Rt△ABC 中,∠C=90°,请验证sin2α + cos2α =1
的结论.证明:在 Rt△ABC中,a2 + b2 = c2,∴ 在 Rt△ABC 中,∠C = 90°,∠BAC = 42°24′, ∠A 的
平分线 AT = 14.7cm,用计算器求 AC 的长(精确到0.001).解:∵ AT 平分∠BAC,且∠BAC = 42°24′,
在 Rt△ACT 中, ,
∴ AC = AT · cos∠CAT = 14.7×cos21°12′
≈13.705(cm).∴ .用计算器求锐角三角函数值及锐角课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
当高跟鞋的鞋底与地面的夹角为11°左
右时,人脚的感觉最舒适,假设某成年人前脚掌到
脚后跟长为15厘米,请问鞋跟在几厘米高度为最佳?11?1. 经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实. 2. 理解锐角正弦的概念,掌握正弦的表示方法.素养目标3. 会根据直角三角形的边长求一个锐角的正弦值,并且能利用正弦求直角三角形的边长. 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?分析:这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管.正弦的定义 解:【思考】在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?ABC50m35mB 'C 'AB'=2B'C' =2×50=100(m) 在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 . 在Rt△ABC中,∠C=90°,由于∠A=45°,所以Rt△ABC是等腰直角三角形,由勾股定理得:因此 在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 . 如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,
你能得出什么结论?
归纳总结 综上可知,在一个Rt△ABC中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于 ,是一个固定值;当∠A=45°时,∠A的对边与斜边的比都等于 ,也是一个固定值.【思考】一般地,当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?ABCA'B'C' 任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?因为∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'. 因此 在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比都是一个固定值. 如图,在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即例如,当∠A=30°时,我们有当∠A=45°时,我们有归纳:注意sinA是一个完整的符号,它表示∠A的正弦,记号里习惯省去角的符号“∠”;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
sinA不表示“sin”乘以“A”. 例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解:(1)在Rt△ABC中,因此(2)在Rt△ABC中,因此利用正弦的定义求有关角的正弦值1.判断对错: (1) ( )
(2) ( )
(3)sin A=0.6m ( )
(4)sin B=0.8 ( )
√√××sin A是一个比值(注意比的顺序),无单位;2)如图②, ( ) ×1) 如图① 图① 图② 2. 在 Rt△ABC中,锐角 A 的对边和斜边同时扩大 100 倍,sinA 的值 ( )
A. 扩大100倍 B. 缩小
C. 不变 D. 不能确定C 例2 如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.解:如图,设点 A (3,0),连接 PA .A (3,0)在Rt△APO中,由勾股定理得因此α在平面直角坐标系内求锐角的正弦值 方法点拨 结合平面直角坐标系求某角的正弦函数值,一般过已知点向 x 轴或 y 轴作垂线,构造直角三角形,再结合勾股定理求解.3.在平面直角坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____345 例3 如图,在 Rt△ABC 中,∠C=90°, ,
BC = 3,求 sinB 及 Rt△ABC 的面积.
提示:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长. 然后再利用勾股定理,求出 AC 的长度,进而求出 sinB 及 Rt△ABC 的面积.利用正弦求直角三角形的边长∴ AB = 3BC =3×3=9.∴∴∴解:∵在 Rt△ABC 中,
∴ 在 Rt△ABC 中,∠C = 90°,sinA = k,
sinB = h,AB = c,则BC = ck,AC = ch. 在 Rt△ABC 中,∠C = 90°,sinA = k,
sinB = h,BC=a,则归纳:,.84.如图:在Rt△ABC中,∠C=90°,AB=10,
, BC的长是 . 例4 在 △ABC 中,∠C=90°,AC=24cm, ,求这个三角形的周长.解:设BC=7x,则AB=25x,在 Rt△ABC中,由勾股定理得即 24x = 24cm,解得 x = 1 cm.故 BC = 7x = 7 cm,AB = 25x = 25 cm.所以 △ABC 的周长为 AB+BC+AC = 7+24+25 = 56 (cm).利用方程和正弦求直角三角形中线段 5.如图,在Rt△ABC中,∠C=90°, , AC=12.
求sinB的值.513解:在Rt △ABC中,
设AB=13x,BC=5x,
由勾股定理得:(5x)2+122=(13x)2解得x=1.所以AB=13,BC=5因此1.(2018?柳州)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.巩固练习A2.(2018?德州)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是_______.巩固练习1. 如图,已知点 P 的坐标是 (a,b),则 sinα 等于( )A. B.
C. D.D2. 在直角三角形 ABC 中,若三边长都扩大 2 倍,则
锐角 A 的正弦值 ( )
A. 扩大 2 倍 B.不变
C. 缩小 D. 无法确定BDA. 4 B. 6 C. 8 D. 1023. 在Rt△ABC中,∠C=90°, ,BC=6,则 AB
的长为 ( )4. 在△ABC中,∠C=90°,如果 ,AB=6,
那么BC=_____.5. 如图,在正方形网格中有 △ABC,则 sin∠ABC 的值为 .解析:∵ , , ,∴∴ AB 2 = BC 2+AC 2,∴ ∠ACB=90°, 如图,在 △ABC中, AB= BC = 5, ,求 △ABC 的面积.D解:作BD⊥AC于点D, ∴又∵ △ABC 为等腰三角形,BD⊥AC,∴ AC=2AD=6,
∴S△ABC=AC×BD÷2=12.
∵ ,求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB. sinB可以由哪两条线段之比得到?若AC=5,CD=3,求sinB的值.解: ∵∠B =∠ACD ∴sinB = sin∠ACD在Rt△ACD中, ∴ ∴ 正弦函数正弦函数的概念正弦函数的应用已知边长求正弦值已知正弦值求边长余弦和正切第二课时返回 如图,在Rt△ABC中,∠C=90°.当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?2. 能灵活运用锐角三角函数进行相关运算.1. 通过类比正弦函数,理解余弦函数、正切函数的定义,进而得到锐角三角函数的概念 .素养目标3. 通过锐角三角函数的学习,培养学生类比学习的能力. 如图, △ABC 和 △DEF 都是直角三角形,
其中∠A =∠D,∠C =∠F = 90°,则
成立吗?为什么?余弦的定义我们来试着证明前面的问题:从而 sinB = sinE,因此 在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关. 如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即归纳:
归纳总结 从上述探究和证明过程,可以得到互余两角的三角函数之间的关系:
对于任意锐角α,有 cos α = sin (90°-α),
或sin α = cos (90°-α). 1. sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2. sinA、 cosA是一个比值(数值).
3. sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.如图:在Rt △ABC中,∠C=90°,正弦余弦注意:1.Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为( )A. B. C. D. A2. Rt△ABC中,∠C=90°,如果AC=4,BC=3,
那么cosB的值为_______ 如图, △ABC 和 △DEF 都是直角三角形,
其中∠A =∠D,∠C =∠F = 90°,则
成立吗?为什么?正切的定义证明:∵∠C=∠F=90°,
∠A=∠D,
∴Rt△ABC ∽ Rt△DEF∴即如图:在Rt △ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的 正切,记作 tanA. 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值. 1.如果两个角互余,那么这两个角的正切值有什么关系?【想一想】2.锐角A的正切值可以等于1吗?为什么?可以大于1吗?3.在Rt?ABC中,∠C=90°,如果
那么tanB的值为( )A. B. C. D. D4. 在Rt?ABC中,∠C=90°,如果
那么tanA的值为_______.锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.sin A= cos A= tan A= 脑中有“图”,心中有“式”锐角三角函数的定义 例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.解:由勾股定理得因此已知直角三角形两边求锐角三角函数的值 方法点拨 已知直角三角形中的两条边求锐角三角函数值的一般思路是:当所涉及的边是已知时,直接利用定义求锐角三角函数值;当所涉及的边未知时,可考虑运用勾股定理的知识求得边的长度,然后根据定义求锐角三角函数值. 5.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是( )6.如图:P是∠ α的边OA上一点,且P点的坐标为(3,4),则cos α
______,tan α = ________.B又已知一边及一锐角三角函数值求函数值 例2 如图,在 Rt△ABC中,∠C = 90°,BC = 6,
,求 cosA、tanB 的值.∴解:∵在Rt△ABC中,
∴解:∵在 Rt△ABC中,∴∴∴7. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8, , 求sinA,cosB 的值.1.(2018?广州)如图,旗杆高AB=8m,某一时刻,旗杆影子
长BC=16m,则tanC=______.巩固练习2. (2018?贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A. B.1
C. D. B1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为:
.==∠A +∠B = 90° 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.解: ∵ ∠ACB=∠ADC =90°,∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,∴∠B = ∠ACD,∴ 如图,在△ABC中,AB=AC=4,BC=6.
求cosB 及 tanB 的值.解:过点 A 作 AD⊥BC 于 D.∵ AB = AC, ∴ BD = CD = 3,在 Rt△ABD 中,D提示:求锐角的三角函数值问题,当图形中没有直角三角形时,可用恰当的方法构造直角三角形.∴∴ 余弦函数和
正切函数余弦正切性质30°、45°、60°角的三角函数值第三课时返回 还记得我们推导正弦关系的时候所得到的结论吗?即 , ,你还能推导出sin60°的值及
30°、45°、60°角的其它三角函数值吗?1. 理解特殊角的三角函数值的由来.
3. 熟记三个特殊锐角的三角函数值,并能准确地加以运用,根据一个特殊角的三角函数值说出这个角.素养目标2. 运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.
设30°所对的直角边长为a,那么斜边长为2a,另一条直角边长=30°60°45°45°特殊角(30°、45°、60°)的三角函数值
∴设两条直角边长为a,则斜边长=∴∴30°、45°、60°角的正弦值、余弦值和正切值如下表:三角函数例1 求下列各式的值:
(1)cos260°+sin260° (2)解: (1) cos260°+sin260°= 1(2)=0特殊角的三角函数值的运算提示:sin260°表示(sin60°)2 方法点拨 含特殊角三角函数值的计算注意事项:
(1)熟记特殊角的锐角三角函数值是关键;
(2)注意运算顺序和法则;
(3)注意特殊角三角函数值的准确代入. 1.计算:
(1) sin30°+ cos45°;解:(1)原式 (2) sin230°+ cos230°-tan45°.(2)原式=1-1=0解:在 Rt△ABC中 ∴ ∠A = 45°.∵利用三角函数值求特殊角例2 (1) 如图,在Rt△ABC中,∠C = 90°, ,
,求 ∠A 的度数;解:在 Rt△ABO中 ∴ α = 60°. (2) 如图,AO 是圆锥的高,OB 是底面半径, ,求 α 的度数.∵2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.解: 由勾股定理∴ ∠ A=30°∠B = 90°- ∠ A = 90°-30°= 60°∴ 例3 已知 △ABC 中的 ∠A 与 ∠B 满足 (1-tanA)2 +|sinB- |=0,试判断 △ABC 的形状. ∴ tanA=1, ,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.特殊角的三角函数值的应用解:∵ (1-tanA)2 + | sinB- |=0,∴ ∠A=45°,∠B=60°,
3. 已知:
求∠A,∠B的度数。解:即∴∴∵巩固练习A1.(2018?大庆)2cos60°=( )
A.1 B. C. D.2.(2019?大庆)计算:(2019-π)0 + -sin60°
解:原式=1+ -1 -=1.下列各式中不正确的是( )
A. B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
2.计算2sin30°-2cos60°+tan45°的结果是( )
A.2 B. C.-1 D.1 BDsin260°+cos260°=13.求满足下列条件的锐角 α .(1) 2sinα - = 0; (2) tanα-1 = 0. ∴ ∠α = 60°.(2) tanα =1, 解:(1) , ∴ ∠α = 45°. 4.在△ABC中,∠A、∠B都是锐角,且 ,
,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定 B5. 在 △ABC 中,若 ,
则∠C = . 120° 6. 求下列各式的值:
(1) 1-2 sin30°cos30°;
(2) 3tan30°-tan45°+2sin60°;
(3) ;
(4)答案:(1)(2)(3) 2(4) 已知 α 为锐角,且 tanα 是方程 x2 + 2x -3 = 0
的一个根,求 2 sin2α + cos2α - tan (α+15°)的值.解:解方程 x2 + 2x - 3 = 0,得 x1 = 1,x2 = -3.
∵ tanα >0,∴ tanα =1,∴ α = 45°.
∴ 2 sin2α + cos2α - tan (α+15°)
= 2 sin245°+cos245°- tan60° 如图,在△ABC中,AD⊥BC,M为AB的中点,∠B=30°,
. 求tan∠BCM.
E解:过点M作ME⊥BC于点E∴CD=AD,又∵M是AB的中点∴BE=DE,AD=2ME.又∵∠B=30°,∵AD⊥BC,∴∴∴30°、45°、60°角的三角函数值通过三角函数值求角度特殊角的三角函数值用计算器求锐角三角函数值
第四课时返回 1填写下表: 前面我们学习了特殊角30°,45°,60°的三角函数值,一些非特殊角(如17°,56°,89°等)的三角函数值又怎么求呢?这一节课我们就学习借助计算器来完成这个任务.1. 会使用科学计算器求锐角的三角函数值.
2. 会根据锐角的三角函数值,借助科学计算器求锐角的大小.素养目标3. 熟练运用计算器解决锐角三角函数中的问题.例如 (1) 用计算器求sin18°的值;第二步:输入角度值18;屏幕显示结果 sin18°= 0.309 016 994.利用计算器求三角函数值、角的度数(2) 用计算器求 tan30°36′ 的值;解:方法①:第二步:输入角度值30.6 (因为30°36′ = 30.6°);屏幕显示答案:0.591 398 351.屏幕显示答案:0.591 398 351.方法②:(3) 已知 sinA = 0.501 8,用计算器求锐角∠A的度数.第二步:输入函数值0. 501 8; 屏幕显示答案: 30.119 158 67°(按实际需要进行
精确).解: 1. 用计算器求下列各式的值(精确到0.0001):
(1) sin47°; (2) sin12°30′;
(3) cos25°18′;(4) sin18°+cos55°-tan59°.答案:(1) 0.7314 (2) 0.2164 (3) 0.9041(4) -0.78172. 已知下列锐角三角函数值,用计算器求锐角 ∠A,
∠B的度数 (结果精确到0.1°):
(1) sinA=0.7,sinB=0.01;
(2) cosA=0.15,cosB=0.8;
(3) tanA=2.4,tanB=0.5.答案:(1) ∠A ≈ 44.4°;∠B ≈ 0.6°.
(2) ∠A ≈ 81.4°;∠B ≈ 36.9°.
(3) ∠A ≈ 67.4°;∠B ≈ 26.6°.(1)通过计算 (可用计算器),比较下列各组数的大小,并提出你的猜想:
① sin30°____2sin15°cos15°;
② sin38°____2sin19°cos19°;
③ sin45°____2sin22.5°cos22.5°;
④ sin60°____2sin30°cos30°;
⑤ sin84°____2sin42°cos42°.
猜想:已知0°<α<45°,则sin2α___2sinαcosα.=利用计算器探索三角函数的性质=====(2) 如图,在△ABC中,AB=AC=1,∠BAC=2α,
请利用面积方法验证 (1) 中的结论.证明:∵ S△ABC = AB · sin2α · AC = sin2α,
S△ABC = ×2ABsinα · ACcosα = sinα · cosα,
∴sin2α=2sinαcosα.2α(1)sin35°= ,cos35°= ,
sin235°= ,cos235°= ;
猜想:
已知0°<α<90°,则 sin2α + cos2α = .0.34200.57350.93970.11700.88300.8192 0.32900.67103.利用计算器求值,并提出你的猜想:1(2)sin20°= , cos20°= ,sin220°= , cos220°= ; 4. 已知:sin254°+ cos2α =1,则锐角 α = . 54° 5. 用计算器比较大小:20sin87° tan87°.> sin20° cos20°,
sin220° cos220°;
sin35° cos35°.< < < (2018?淄博)一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是( )
A. B.
C. D.巩固练习A1. 下列式子中,不成立的是( )
A.sin35°= cos55°
B.sin25°+ sin40°= sin65°
C. cos47°= sin43°
D.sin218°+ cos218°=1B2. 用计算器求sin24°37′18″的值,以下按键顺序正确的是 ( )
A.
B.
C.
D. A(1) sin40°≈ (精确到0.0001);
(2) tan63°27′≈ (精确到 0.0001);
(3) cos18°59′27″≈ (精确到 0.0001);
(4) 若sinα = 0.5225,则 α ≈ (精确到 0.1°);
(5) 若cosα = 0.3145,则 α ≈ (精确到 0.1°).0.64282.001331.5°3. 利用计算器求值:71.7°0.9452 如图,在 Rt△ABC 中,∠C=90°,请验证sin2α + cos2α =1
的结论.证明:在 Rt△ABC中,a2 + b2 = c2,∴ 在 Rt△ABC 中,∠C = 90°,∠BAC = 42°24′, ∠A 的
平分线 AT = 14.7cm,用计算器求 AC 的长(精确到0.001).解:∵ AT 平分∠BAC,且∠BAC = 42°24′,
在 Rt△ACT 中, ,
∴ AC = AT · cos∠CAT = 14.7×cos21°12′
≈13.705(cm).∴ .用计算器求锐角三角函数值及锐角课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
