人教版九年级数学下册第二十八章 锐角三角函数28.2.1 解直角三角形课件(26张PPT)
文档属性
| 名称 | 人教版九年级数学下册第二十八章 锐角三角函数28.2.1 解直角三角形课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-09 07:21:18 | ||
图片预览








文档简介
课件26张PPT。28.2 解直角三角形及其应用人教版 数学 九年级 下册28.2.1解直角三角形 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能够安全使用这个梯子吗?1. 了解解直角三角形的意义和条件. 2. 理解直角三角形中的五个元素之间的联系.素养目标3. 能根据直角三角形中除直角以外的两个元素(至少有一个是边),解直角三角形.利用计算器可得 .根据以上条件可以求出塔身中心线与垂直中心线的夹角.
你愿意试着计算一下吗? 如图,设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过B点向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.解直角三角形的概念在Rt△ABC中,不能不能一角一角一边两角 (2)根据∠A=60°,∠B=30°, 你能求出这个三角形的其他元素吗? (1)根据∠A= 60°,你能求出这个三角形的其他元素吗? (3)根据∠A= 60°,斜边AB=4,你能求出这个三角形的其他元素吗?∠B AC BC两边∠A ∠B AB (4)根据 ,AC= 2 , 你能求出这个三角形的
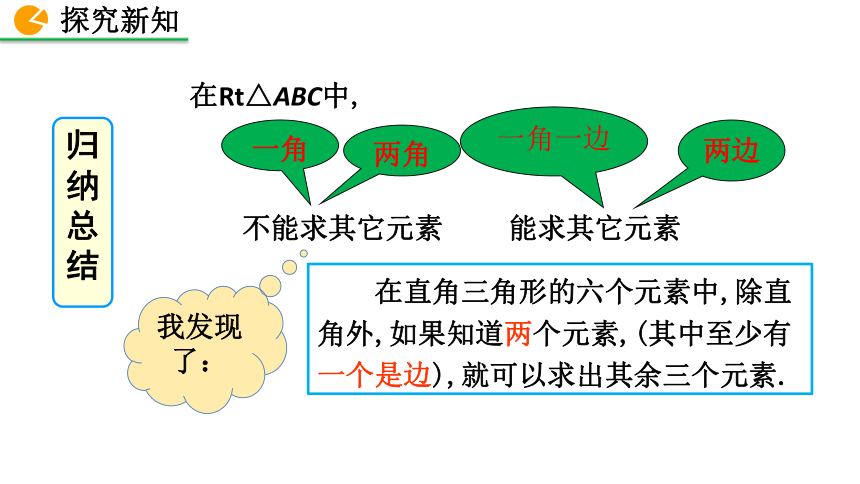
其他元素吗?在Rt△ABC中,两角不能求其它元素一角能求其它元素归纳总结解直角三角形的依据:a2+b2=c2(勾股定理);(1)三边之间的关系: (2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系: 由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.
归纳总结解直角三角形的原则:(1)有斜(斜边)用弦(正弦、余弦),无斜(斜边)用切(正切);(2)宁乘勿除:选取便于计算的关系式,若能用乘法计算就不用除法计算;(3)取原避中:若能用原始数据计算,应避免使用中间数据求解. 如图,在Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?知道两边解直角三角形 例1 如图,在Rt△ABC中,∠C = 90°, ,
,解这个直角三角形.已知两边解直角三角形∴1.在Rt△ABC中,∠C=90°, a = 30 , b = 20,
解这个直角三角形.解:根据勾股定理∵∴ 如图,在Rt△ABC中,根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?75°已知一边和一锐角解直角三角形 例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).解:已知一边和一锐角解直角三角形2.在Rt△ABC,∠C=90°, ∠A=45°, c=4 解这个直角三角形.
45°c=4解:∵ ∠A=45°
∴ ∠B=90°—∠A=45°,ab∵∴∵∴解:过点A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD= AC · sinC = 2sin45°= .
在△ABD中,∠B=30°,
3. 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.D∴∴ 如图,在Rt△ABC 中,∠C=90°, ,
BC = 5, 试求AB的长.设已知一边和三角函数值解直角三角形∴∵∴∴ (舍去)∴ AB的长为4. 在Rt△ABC中,∠C=90°,sinA = 0.8 ,BC=8,则
AC的值为( )
A.4 B.6 C.8 D.10 B5. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
,则菱形的周长是 ( )
A.10 B.20
C.40 D.28 C(2018?自贡)如图,在△ABC中,BC=12, ,B=30°;求AC和AB的长.
巩固练习解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°, H∴ , ,∴ ,∴AH=8,在Rt△ACH中, , ∴ .1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角D2. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则
AC =______ (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).3. 如图,已知Rt△ABC中,斜边BC上的高AD=3,
则 AC 的长为 . 243.75 4. 在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形. ∵∴∴ 如图,已知 AC = 4,求 AB 和 BC 的长.分析:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D解:如图,作CD⊥AB于点D,在Rt△ACD中,∵∠A=30°,
∴∠ACD=90°-∠A=60°,∴BD=CD=2.∴ 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC
的平分线 ,解这个直角三角形.∵ AD平分∠BAC,∴∠CAD=30° ∴∴∠CAB=60°, ∠B=30°,解直角三角形依据解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素.勾股定理两锐角互余锐角的三角函数课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
(1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1m)?
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能够安全使用这个梯子吗?1. 了解解直角三角形的意义和条件. 2. 理解直角三角形中的五个元素之间的联系.素养目标3. 能根据直角三角形中除直角以外的两个元素(至少有一个是边),解直角三角形.利用计算器可得 .根据以上条件可以求出塔身中心线与垂直中心线的夹角.
你愿意试着计算一下吗? 如图,设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过B点向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.解直角三角形的概念在Rt△ABC中,不能不能一角一角一边两角 (2)根据∠A=60°,∠B=30°, 你能求出这个三角形的其他元素吗? (1)根据∠A= 60°,你能求出这个三角形的其他元素吗? (3)根据∠A= 60°,斜边AB=4,你能求出这个三角形的其他元素吗?∠B AC BC两边∠A ∠B AB (4)根据 ,AC= 2 , 你能求出这个三角形的
其他元素吗?在Rt△ABC中,两角不能求其它元素一角能求其它元素归纳总结解直角三角形的依据:a2+b2=c2(勾股定理);(1)三边之间的关系: (2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系: 由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.
归纳总结解直角三角形的原则:(1)有斜(斜边)用弦(正弦、余弦),无斜(斜边)用切(正切);(2)宁乘勿除:选取便于计算的关系式,若能用乘法计算就不用除法计算;(3)取原避中:若能用原始数据计算,应避免使用中间数据求解. 如图,在Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?知道两边解直角三角形 例1 如图,在Rt△ABC中,∠C = 90°, ,
,解这个直角三角形.已知两边解直角三角形∴1.在Rt△ABC中,∠C=90°, a = 30 , b = 20,
解这个直角三角形.解:根据勾股定理∵∴ 如图,在Rt△ABC中,根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?75°已知一边和一锐角解直角三角形 例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).解:已知一边和一锐角解直角三角形2.在Rt△ABC,∠C=90°, ∠A=45°, c=4 解这个直角三角形.
45°c=4解:∵ ∠A=45°
∴ ∠B=90°—∠A=45°,ab∵∴∵∴解:过点A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD= AC · sinC = 2sin45°= .
在△ABD中,∠B=30°,
3. 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.D∴∴ 如图,在Rt△ABC 中,∠C=90°, ,
BC = 5, 试求AB的长.设已知一边和三角函数值解直角三角形∴∵∴∴ (舍去)∴ AB的长为4. 在Rt△ABC中,∠C=90°,sinA = 0.8 ,BC=8,则
AC的值为( )
A.4 B.6 C.8 D.10 B5. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
,则菱形的周长是 ( )
A.10 B.20
C.40 D.28 C(2018?自贡)如图,在△ABC中,BC=12, ,B=30°;求AC和AB的长.
巩固练习解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°, H∴ , ,∴ ,∴AH=8,在Rt△ACH中, , ∴ .1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角D2. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则
AC =______ (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).3. 如图,已知Rt△ABC中,斜边BC上的高AD=3,
则 AC 的长为 . 243.75 4. 在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形. ∵∴∴ 如图,已知 AC = 4,求 AB 和 BC 的长.分析:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D解:如图,作CD⊥AB于点D,在Rt△ACD中,∵∠A=30°,
∴∠ACD=90°-∠A=60°,∴BD=CD=2.∴ 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC
的平分线 ,解这个直角三角形.∵ AD平分∠BAC,∴∠CAD=30° ∴∴∠CAB=60°, ∠B=30°,解直角三角形依据解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素.勾股定理两锐角互余锐角的三角函数课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
