人教版九年级数学下册第二十八章 锐角三角函数28.2.2应用举例课件3课时(86张PPT)
文档属性
| 名称 | 人教版九年级数学下册第二十八章 锐角三角函数28.2.2应用举例课件3课时(86张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-09 07:22:48 | ||
图片预览






文档简介
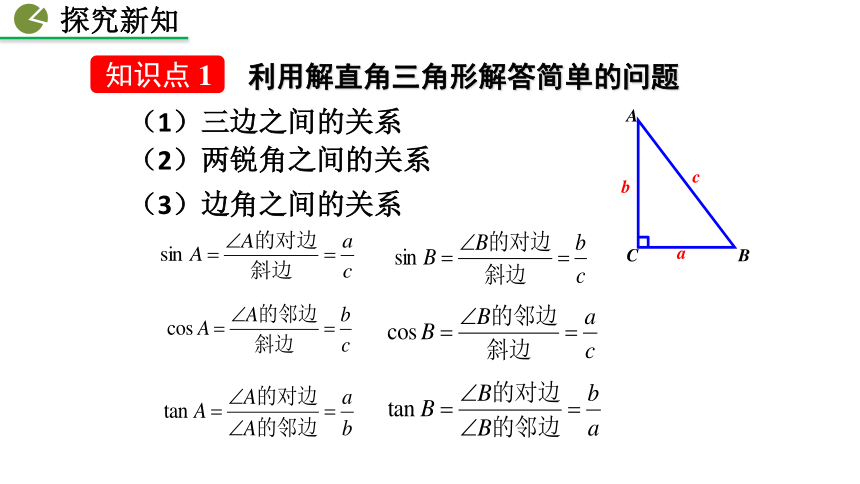
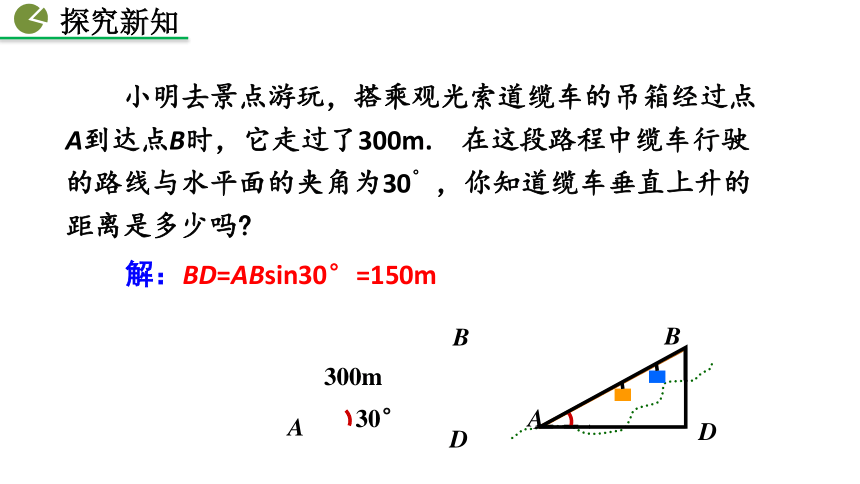
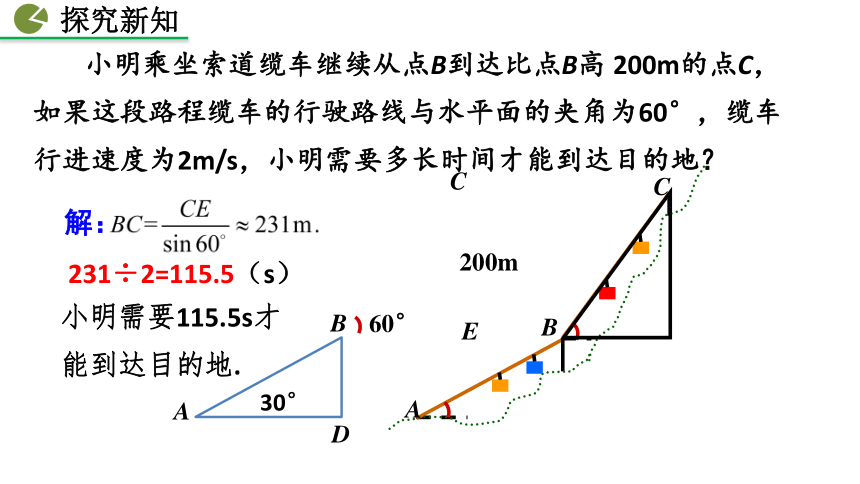
课件86张PPT。28.2 解直角三角形及其应用第一课时第二课时第三课时人教版 数学 九年级 下册28.2.2 应用举例解直角三角形的简单应用第一课时返回 高跟鞋深受很多女性的喜爱,但有时候,如果鞋跟太高,也有可能“喜剧”变“悲剧”.3. 体会数学在解决实际问题中的应用,逐步培养学生分析问题、解决问题的能力.1. 巩固解直角三角形相关知识 .素养目标2. 能从实际问题中构造直角三角形,会把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题.(2)两锐角之间的关系(3)边角之间的关系(1)三边之间的关系 利用解直角三角形解答简单的问题 小明去景点游玩,搭乘观光索道缆车的吊箱经过点A到达点B时,它走过了300m. 在这段路程中缆车行驶的路线与水平面的夹角为30° ,你知道缆车垂直上升的距离是多少吗?ABABD30°300m解:BD=ABsin30°=150mDABC 小明乘坐索道缆车继续从点B到达比点B高 200m的点C, 如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为2m/s,小明需要多长时间才能到达目的地?ABDCE60°200m小明需要115.5s才
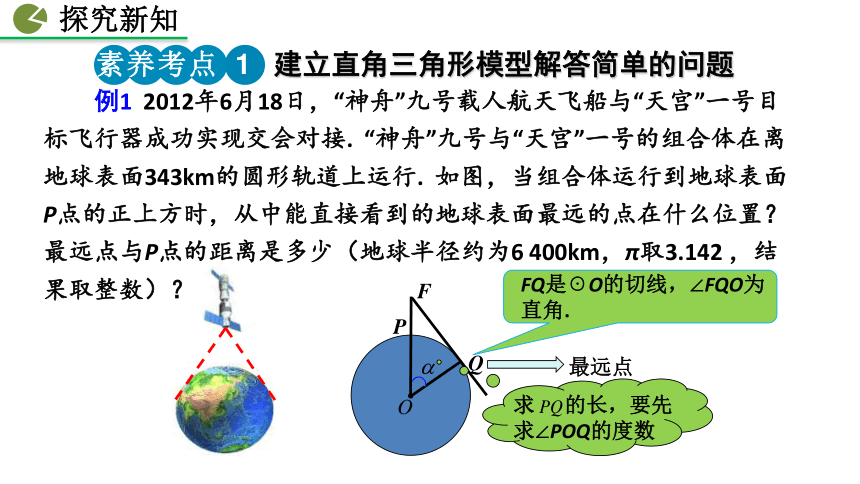
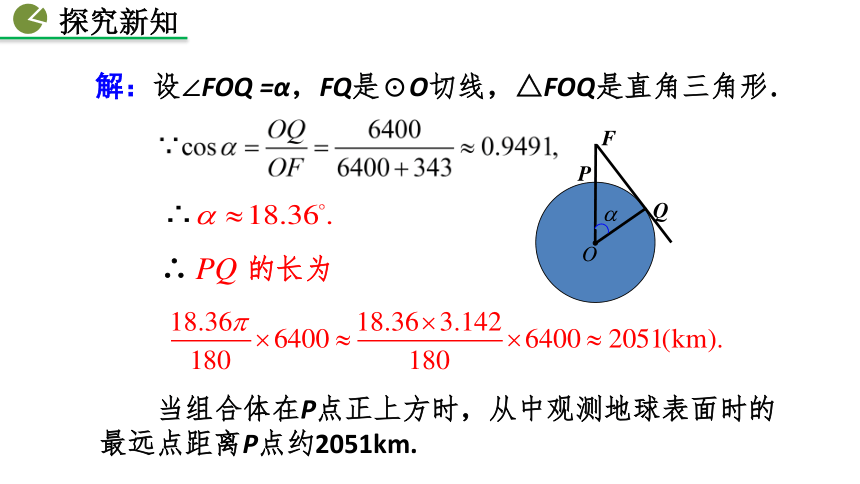
能到达目的地.解:231÷2=115.5(s)30° 例1 2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神舟”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行. 如图,当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6 400km,π取3.142 ,结果取整数)?最远点建立直角三角形模型解答简单的问题解:设∠FOQ =α,FQ是⊙O切线,△FOQ是直角三角形. 当组合体在P点正上方时,从中观测地球表面时的最远点距离P点约2051km.∴ 的长为【讨论】从前面的例题解答中,你能体会到解直角三角形的应用前提条件是什么吗?如何进行?【方法点拨】一般情况下,直角三角形是求解或运用三角函数值的前提条件,故当题目中提供的并非直角三角形时,需添加辅助线构造直角三角形,然后运用三角函数解决问题.小结
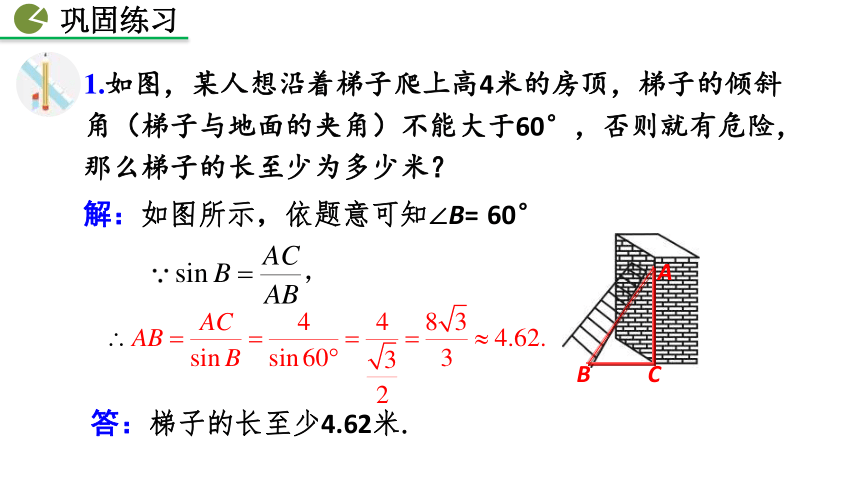
归纳总结解直角三角形的应用:(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;(3)得到数学问题答案;(4)得到实际问题答案。注:数学问题的解符合实际意义才可以成为实际问题的解.1.如图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米?ABC解:如图所示,依题意可知∠B= 60° 答:梯子的长至少4.62米. 例2 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?0.5m3m60°建立直角三角形模型解答生活问题0.5m3mABCDE60°分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:已知 DE=0.5m,AD=AB=3m,∠DAB=60°,△ACB为直角三角形,求CE的长度.解:∵∠CAB=60°,AD=AB=3m,∴AC=ABcos∠CAB=1.5m,∴ CD=AD-AC=1.5m,∴ CE=AD+DE=2.0m.即秋千踏板与地面的最大距离为2.0m.2. (1)小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m,两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?北ABDC20m15mEF南解:过点E作EF∥BC,∴∠AFE=90°,FE=BC=15m.即南楼的影子在北楼上的高度为∴∴(2) 小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC至少应为多少米?AB20m?m南答案:BC至少为 (2018?台州)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)巩固练习图1图2巩固练习解:作CE⊥BD于E,AF⊥CE于F,易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°,
在Rt△ACF中,∵ ,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.图2EF1. 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:
从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、 AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两
树距离的有( )
A. 0组 B. 1组 C. 2组 D. 3组 D2. 如图,要测量B点到河岸AD的距离,在A点测得
∠BAD=30°,在C点测得∠BCD=60°,又测得
AC=100米,则B点到河岸AD的距离为( )A. 100米 B. 米
C. 米 D. 50米B3. 一次台风将一棵大树刮断,经测量,大树刮断一端的
着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为45°,则这棵大树高是 米.ACB4米45° “欲穷千里目,更上一层楼”是唐代诗人李白的不朽诗句.如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗(设 代表地面,O为地球球心,C是地面上一点,
=500km,地球的半径为6370 km,cos4.5°= 0.997)?解:设登到B处,视线BC在C点与地球相切,也就是
看C点,AB就是“楼”的高度,∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即19000m. 这是不存在的. 在Rt△OCB中,∠O 如图,在电线杆上的C处引拉线CE,CF固定电线杆. 拉线CE和地面成60°角,在离电线杆6米的A处测得AC与水平面的夹角为30°,已知A与地面的距离为1.5米,求拉线CE的长.(结果保留根号) G解:作AG⊥CD于点G,
则AG=BD=6米,DG=AB=1.5米.∴(米).∴CD=CG+DG= ( +1.5) (米),∴ (米).利用解直角三角形解决实际问题的一般过程:1. 将实际问题抽象为数学问题;2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;画出平面图形,转化为解直角三角形的问题3. 得到数学问题的答案;4. 得到实际问题的答案.利用俯角和仰角解直角三角形第二课时返回 青青草原上,灰太狼每天都想着如何抓羊,而且屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40 m,若灰太狼以 5 m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)(假设懒洋洋不动) 1. 使学生了解仰角、俯角的概念,并能够根据直角三角形的知识解决实际问题.
2.在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路.素养目标3. 进一步培养学生分析问题、解决问题的能力. 在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角,视线在水平线下方的叫做俯角.俯角、仰角问题 例1 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°. 在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.仰角水平线俯角一个观测点构造两个直角三角形解答实际问题解:如图,α = 30°,β= 60°, AD=120.答:这栋楼高约为277m.(m) 方法点拨解决与仰角、俯角有关的实际问题的方法 根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形使问题获解.1. 如图,在电线杆上离地面高度5m的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示). 例2 如图,直升飞机在长400米的跨江大桥AB的上方P点
处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,
tan 37°≈0.75)
AB37°45°400米P两个观测点构造两个直角三角形解答实际问题ABO37°45°400米P设PO=x米,在Rt△POB中,∠PBO=45°,在Rt△POA中,∠PAB=37°,OB=PO= x米.解得x=1200.解:作PO⊥AB交AB的延长线于O.即故飞机的高度为1200米.2. 如图,为了测出某塔CD的高度,在塔前的平地上选择
一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
(1) 求点B到AD的距离; 答案:点B到AD的距离为20m.E(2) 求塔高CD(结果用根号表示).解:在Rt△ABE中,
∵∠A=30°,∴∠ABE=60°,
∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20m,
则 (m),
在Rt△ADC中,∠A=30°,
答:塔高CD为 m.∴ (m).E(2018?长春)如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为( )
A. 800sinα米 B. 800tanα米
C. 米 D. 米巩固练习D1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘
小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=____米.
2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.1003. 为测量松树AB的高度,一个人站在距松树15米的E处,
测得仰角∠ACD=52°,已知人的高度是1.72米,则
树高 (精确到0.1米). 20.9 米4. 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?解:由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m. ∴D′B′=x·tan60°,C′B′=x·tan30°,∴x·tan60°-x·tan30°=50,∵∴ ∠D′AB′=60°,∠C′AB′=30°,设AB′=x m.∴∴ 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m.在Rt△ACD中 ,∴AB=AC-BC=55.2-40=15.2 (m).∴AC=DC·tan∠ADC=tan54°×40≈1.38×40=55.2(m)解:由题意,AC=AB=610(米). 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;解:DE=AC=610(米),
在Rt△BDE中, .(2) 求大楼的高度CD(精确到1米)∴ BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°
≈116(米).利用仰俯角解直角三角形仰角、俯角的概念运用解直角三角形解决仰角、俯角问题利用方向角、坡度解直角三角形第三课时返回 宜宾是国家级历史文化名城,大观楼是其标志性建筑之一
(如图①).喜爱数学的小伟决定用所学的知识测量大观楼的高度,如图②所示,他站在点B处利用测角仪测得大观楼最高点P的仰角为45°,又前进了12 m到达点A处,测得点P的仰角为60°.请你帮助小伟算一算大观楼的高度(测角仪的高度忽略不计,结果保留整数).图②图①1. 正确理解方向角、坡度的概念. 2. 能运用解直角三角形知识解决方向角、坡度的问题.素养目标3. 能够解决与解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等.方向角的定义: 指北或指南方向线与目标方向线所成的小于90°的角叫做方向角。北偏东30°南偏西45°方向角的有关问题也叫西南方向注意(1)因为方向角是指北或指南方向线与目标方向线所成的角,所以方向角通常都写成“北偏……”, “南偏……”,的形式.(2)解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.(3)观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助于此性质进行角度转换. 例1 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?有关方向角的实际问题——距离解:如图 ,在Rt△APC中,PC=PA·cos(90°-65°)=80×cos25°≈80×0.91=72.505.在Rt△BPC中,∠B=34°,因此,当海轮到达位于灯塔P的南偏东34°方向时,
它距离灯塔P大约130n mile.
归纳总结利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.1.美丽的东昌湖滨位于江北水城,周边景点密布.如图所示,A、B为湖滨的两个景点,C为湖心一个景点.景点B在景点C的正东,从景点A看,景点B在北偏东75°方向,景点C在北偏东30°方向.一游客自景点A驾船以每分钟20 m的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?解:根据题意,得AC=20×10=200(m).
如图所示,过点A作AD⊥BC于点D.
在Rt△ADC中, ,
DC=AC·sin ∠CAD=200·sin 30°=100.
在Rt△ADB中, . ∴ . 例2 海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BAC60°有关方向角的实际问题——预测路线30°解:过A作AF⊥BC于点F,
则AF的长是A到BC的最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,
∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF
=60°-30°
=30°.EF又∵∠ABC =∠DBF-∠DBA
= 90°-60°=30°=∠BAC,
∴BC=AC=12海里,
,
故渔船继续向正东方向行驶,
没有触礁的危险.∴ (海里),2. 如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区
(参考数据: ≈1.732, ≈1.414)?北东解:过点P作PC⊥AB于点C.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
即 ,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公路不会
穿越保护区.C 解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,我们无法直接测量,我们又该如何呢?坡度、坡角有关的问题【思考】如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?如何用数量来刻画哪条路陡呢?坡角:坡面与水平面的夹角叫做坡角,用字母 α 表示。坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 i 表示,如图,坡度通常写成
的形式。坡度越大
坡角越大
坡面越陡 α水平面坡面(1)斜坡的坡度是 ,则坡角α =____度.
(2)斜坡的坡角是45° ,则坡比是 _____.
(3)斜坡长是12米,坡高6米,则坡比是_______.
301 : 13.完成下列各题 例3 如图,防洪大堤的横截面是梯形 ABCD,其中
AD∥BC,α=60°,汛期来临前对其进行了加固,改造
后的背水面坡角β=45°.若原坡长AB=20m,求改造后
的坡长AE.(结果保留根号) 利用坡度、坡角解答大坝问题解:过点A作AF⊥BC于点F,
在Rt△ABF中,
∠ABF =∠α=60°,
则AF=AB·sin60°= (m),
在Rt△AEF中,∠E=∠β=45°,
则 (m).
故改造后的坡长AE 为 m.F4. 如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比 .求加固后坝底增加的宽度AF.
(结果保留根号)GH解:作DG⊥AB于G,EH⊥AB于H,
则GH=DE=2米,EH=DG=10米.(米),(米).又∵AG=DG=10米,故加固后坝底增加的宽度AF为 米.∴ (米). 例4 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?i=1:2利用坡度、坡角解答山坡问题在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,因此 α≈26.57°.答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.从而 BC=240×sin26.57°≈107.3(m).因此BACi=1:25. 如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.30°答案:点B和点C的水平距离为 米.E1.(2018?徐州)如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据: ,
巩固练习巩固练习解:在Rt△CDE中,∵ ,
∴ , ∴EF=AD=6m,AF=DE=7m∵四边形AFED是矩形,答:该坝的坝高和坝底宽分别为7m和25.1m.在Rt△ABF中,∵∠B=45°,∴BF=AF=7m,∴BC=BF+EF+EC≈7+6+12.12=25.12≈25.1(m),2.(2018?重庆)如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走 20 米到达点C,再经过一段坡度(或坡比)为 i=1:0.75、坡长为10 米的斜坡CD 到达点 D,然后再沿水平方向向右行走40 米到达点 E(A,
B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米
C.27.4米 D.28.8米 A1. 如图,C岛在A岛的北偏东50°方向,C岛在B岛
的北偏西40°方向,则从C岛看A,B两岛的视角
∠ACB等于 . 90°2. 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是( ) A. 10分钟 B. 15分钟
C. 20分钟 D. 25分钟B3. 如图,海上B、C两岛分别位于A岛的正东和正北方向,一艘
船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C
岛,此时测得B岛在C岛的南偏东43°方向,则A、B两岛之间的距离为 . (结果精确到0.1海里,
参考数据:sin43°=0.68, cos43°=0.73,
tan43°=0.93)
33.5海里 水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB
的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1) 斜坡CD的坡角α (精确到 1°);
i=1:3解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,由计算器可算得α≈22°.故斜坡CD的坡角α 为22°.解:分别过点B、C作BE⊥AD于E ,CF⊥AD于F ,
由题意可知BE=CF=23m , EF=BC=6m.在Rt△ABE中,(2) 坝底AD与斜坡AB的长度 (精确到0.1m). EFi=1:3在Rt△ABE中,由勾股定理可得在Rt△DCF中,同理可得故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.∴AD=AE+EF+FD=69+6+57.5=132.5(m)FD=2.5CF=2.5×23=57.5(m),EF解:作DE⊥AB于E , CF⊥AB于F ,
由题意可知DE=CF=4 (米),CD=EF=12 (米). 一段路基的横断面是梯形,高为 4 米,上底的宽是12 米,
路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽 (精确到0.1米, , ). ?
45°30°4米12米ABCD 在Rt△ADE中,EF
在Rt△BCF中,同理可得
因此 AB=AE+EF+BF≈4+12+6.93≈22.9 (米).
答: 路基下底的宽约为22.9米.(米).(米).解直角三角形的应用坡度问题方向角问题坡角坡度(或坡比) 课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
能到达目的地.解:231÷2=115.5(s)30° 例1 2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神舟”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行. 如图,当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6 400km,π取3.142 ,结果取整数)?最远点建立直角三角形模型解答简单的问题解:设∠FOQ =α,FQ是⊙O切线,△FOQ是直角三角形. 当组合体在P点正上方时,从中观测地球表面时的最远点距离P点约2051km.∴ 的长为【讨论】从前面的例题解答中,你能体会到解直角三角形的应用前提条件是什么吗?如何进行?【方法点拨】一般情况下,直角三角形是求解或运用三角函数值的前提条件,故当题目中提供的并非直角三角形时,需添加辅助线构造直角三角形,然后运用三角函数解决问题.小结
归纳总结解直角三角形的应用:(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;(3)得到数学问题答案;(4)得到实际问题答案。注:数学问题的解符合实际意义才可以成为实际问题的解.1.如图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米?ABC解:如图所示,依题意可知∠B= 60° 答:梯子的长至少4.62米. 例2 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?0.5m3m60°建立直角三角形模型解答生活问题0.5m3mABCDE60°分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:已知 DE=0.5m,AD=AB=3m,∠DAB=60°,△ACB为直角三角形,求CE的长度.解:∵∠CAB=60°,AD=AB=3m,∴AC=ABcos∠CAB=1.5m,∴ CD=AD-AC=1.5m,∴ CE=AD+DE=2.0m.即秋千踏板与地面的最大距离为2.0m.2. (1)小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m,两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?北ABDC20m15mEF南解:过点E作EF∥BC,∴∠AFE=90°,FE=BC=15m.即南楼的影子在北楼上的高度为∴∴(2) 小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC至少应为多少米?AB20m?m南答案:BC至少为 (2018?台州)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)巩固练习图1图2巩固练习解:作CE⊥BD于E,AF⊥CE于F,易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°,
在Rt△ACF中,∵ ,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.图2EF1. 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:
从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、 AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两
树距离的有( )
A. 0组 B. 1组 C. 2组 D. 3组 D2. 如图,要测量B点到河岸AD的距离,在A点测得
∠BAD=30°,在C点测得∠BCD=60°,又测得
AC=100米,则B点到河岸AD的距离为( )A. 100米 B. 米
C. 米 D. 50米B3. 一次台风将一棵大树刮断,经测量,大树刮断一端的
着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为45°,则这棵大树高是 米.ACB4米45° “欲穷千里目,更上一层楼”是唐代诗人李白的不朽诗句.如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗(设 代表地面,O为地球球心,C是地面上一点,
=500km,地球的半径为6370 km,cos4.5°= 0.997)?解:设登到B处,视线BC在C点与地球相切,也就是
看C点,AB就是“楼”的高度,∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即19000m. 这是不存在的. 在Rt△OCB中,∠O 如图,在电线杆上的C处引拉线CE,CF固定电线杆. 拉线CE和地面成60°角,在离电线杆6米的A处测得AC与水平面的夹角为30°,已知A与地面的距离为1.5米,求拉线CE的长.(结果保留根号) G解:作AG⊥CD于点G,
则AG=BD=6米,DG=AB=1.5米.∴(米).∴CD=CG+DG= ( +1.5) (米),∴ (米).利用解直角三角形解决实际问题的一般过程:1. 将实际问题抽象为数学问题;2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;画出平面图形,转化为解直角三角形的问题3. 得到数学问题的答案;4. 得到实际问题的答案.利用俯角和仰角解直角三角形第二课时返回 青青草原上,灰太狼每天都想着如何抓羊,而且屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40 m,若灰太狼以 5 m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)(假设懒洋洋不动) 1. 使学生了解仰角、俯角的概念,并能够根据直角三角形的知识解决实际问题.
2.在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路.素养目标3. 进一步培养学生分析问题、解决问题的能力. 在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角,视线在水平线下方的叫做俯角.俯角、仰角问题 例1 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°. 在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.仰角水平线俯角一个观测点构造两个直角三角形解答实际问题解:如图,α = 30°,β= 60°, AD=120.答:这栋楼高约为277m.(m) 方法点拨解决与仰角、俯角有关的实际问题的方法 根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形使问题获解.1. 如图,在电线杆上离地面高度5m的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示). 例2 如图,直升飞机在长400米的跨江大桥AB的上方P点
处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,
tan 37°≈0.75)
AB37°45°400米P两个观测点构造两个直角三角形解答实际问题ABO37°45°400米P设PO=x米,在Rt△POB中,∠PBO=45°,在Rt△POA中,∠PAB=37°,OB=PO= x米.解得x=1200.解:作PO⊥AB交AB的延长线于O.即故飞机的高度为1200米.2. 如图,为了测出某塔CD的高度,在塔前的平地上选择
一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
(1) 求点B到AD的距离; 答案:点B到AD的距离为20m.E(2) 求塔高CD(结果用根号表示).解:在Rt△ABE中,
∵∠A=30°,∴∠ABE=60°,
∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20m,
则 (m),
在Rt△ADC中,∠A=30°,
答:塔高CD为 m.∴ (m).E(2018?长春)如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为( )
A. 800sinα米 B. 800tanα米
C. 米 D. 米巩固练习D1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘
小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=____米.
2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.1003. 为测量松树AB的高度,一个人站在距松树15米的E处,
测得仰角∠ACD=52°,已知人的高度是1.72米,则
树高 (精确到0.1米). 20.9 米4. 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?解:由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m. ∴D′B′=x·tan60°,C′B′=x·tan30°,∴x·tan60°-x·tan30°=50,∵∴ ∠D′AB′=60°,∠C′AB′=30°,设AB′=x m.∴∴ 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m.在Rt△ACD中 ,∴AB=AC-BC=55.2-40=15.2 (m).∴AC=DC·tan∠ADC=tan54°×40≈1.38×40=55.2(m)解:由题意,AC=AB=610(米). 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;解:DE=AC=610(米),
在Rt△BDE中, .(2) 求大楼的高度CD(精确到1米)∴ BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°
≈116(米).利用仰俯角解直角三角形仰角、俯角的概念运用解直角三角形解决仰角、俯角问题利用方向角、坡度解直角三角形第三课时返回 宜宾是国家级历史文化名城,大观楼是其标志性建筑之一
(如图①).喜爱数学的小伟决定用所学的知识测量大观楼的高度,如图②所示,他站在点B处利用测角仪测得大观楼最高点P的仰角为45°,又前进了12 m到达点A处,测得点P的仰角为60°.请你帮助小伟算一算大观楼的高度(测角仪的高度忽略不计,结果保留整数).图②图①1. 正确理解方向角、坡度的概念. 2. 能运用解直角三角形知识解决方向角、坡度的问题.素养目标3. 能够解决与解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等.方向角的定义: 指北或指南方向线与目标方向线所成的小于90°的角叫做方向角。北偏东30°南偏西45°方向角的有关问题也叫西南方向注意(1)因为方向角是指北或指南方向线与目标方向线所成的角,所以方向角通常都写成“北偏……”, “南偏……”,的形式.(2)解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.(3)观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助于此性质进行角度转换. 例1 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?有关方向角的实际问题——距离解:如图 ,在Rt△APC中,PC=PA·cos(90°-65°)=80×cos25°≈80×0.91=72.505.在Rt△BPC中,∠B=34°,因此,当海轮到达位于灯塔P的南偏东34°方向时,
它距离灯塔P大约130n mile.
归纳总结利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.1.美丽的东昌湖滨位于江北水城,周边景点密布.如图所示,A、B为湖滨的两个景点,C为湖心一个景点.景点B在景点C的正东,从景点A看,景点B在北偏东75°方向,景点C在北偏东30°方向.一游客自景点A驾船以每分钟20 m的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?解:根据题意,得AC=20×10=200(m).
如图所示,过点A作AD⊥BC于点D.
在Rt△ADC中, ,
DC=AC·sin ∠CAD=200·sin 30°=100.
在Rt△ADB中, . ∴ . 例2 海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BAC60°有关方向角的实际问题——预测路线30°解:过A作AF⊥BC于点F,
则AF的长是A到BC的最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,
∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF
=60°-30°
=30°.EF又∵∠ABC =∠DBF-∠DBA
= 90°-60°=30°=∠BAC,
∴BC=AC=12海里,
,
故渔船继续向正东方向行驶,
没有触礁的危险.∴ (海里),2. 如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区
(参考数据: ≈1.732, ≈1.414)?北东解:过点P作PC⊥AB于点C.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
即 ,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公路不会
穿越保护区.C 解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,我们无法直接测量,我们又该如何呢?坡度、坡角有关的问题【思考】如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?如何用数量来刻画哪条路陡呢?坡角:坡面与水平面的夹角叫做坡角,用字母 α 表示。坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 i 表示,如图,坡度通常写成
的形式。坡度越大
坡角越大
坡面越陡 α水平面坡面(1)斜坡的坡度是 ,则坡角α =____度.
(2)斜坡的坡角是45° ,则坡比是 _____.
(3)斜坡长是12米,坡高6米,则坡比是_______.
301 : 13.完成下列各题 例3 如图,防洪大堤的横截面是梯形 ABCD,其中
AD∥BC,α=60°,汛期来临前对其进行了加固,改造
后的背水面坡角β=45°.若原坡长AB=20m,求改造后
的坡长AE.(结果保留根号) 利用坡度、坡角解答大坝问题解:过点A作AF⊥BC于点F,
在Rt△ABF中,
∠ABF =∠α=60°,
则AF=AB·sin60°= (m),
在Rt△AEF中,∠E=∠β=45°,
则 (m).
故改造后的坡长AE 为 m.F4. 如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比 .求加固后坝底增加的宽度AF.
(结果保留根号)GH解:作DG⊥AB于G,EH⊥AB于H,
则GH=DE=2米,EH=DG=10米.(米),(米).又∵AG=DG=10米,故加固后坝底增加的宽度AF为 米.∴ (米). 例4 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?i=1:2利用坡度、坡角解答山坡问题在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,因此 α≈26.57°.答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.从而 BC=240×sin26.57°≈107.3(m).因此BACi=1:25. 如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.30°答案:点B和点C的水平距离为 米.E1.(2018?徐州)如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据: ,
巩固练习巩固练习解:在Rt△CDE中,∵ ,
∴ , ∴EF=AD=6m,AF=DE=7m∵四边形AFED是矩形,答:该坝的坝高和坝底宽分别为7m和25.1m.在Rt△ABF中,∵∠B=45°,∴BF=AF=7m,∴BC=BF+EF+EC≈7+6+12.12=25.12≈25.1(m),2.(2018?重庆)如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走 20 米到达点C,再经过一段坡度(或坡比)为 i=1:0.75、坡长为10 米的斜坡CD 到达点 D,然后再沿水平方向向右行走40 米到达点 E(A,
B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米
C.27.4米 D.28.8米 A1. 如图,C岛在A岛的北偏东50°方向,C岛在B岛
的北偏西40°方向,则从C岛看A,B两岛的视角
∠ACB等于 . 90°2. 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是( ) A. 10分钟 B. 15分钟
C. 20分钟 D. 25分钟B3. 如图,海上B、C两岛分别位于A岛的正东和正北方向,一艘
船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C
岛,此时测得B岛在C岛的南偏东43°方向,则A、B两岛之间的距离为 . (结果精确到0.1海里,
参考数据:sin43°=0.68, cos43°=0.73,
tan43°=0.93)
33.5海里 水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB
的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1) 斜坡CD的坡角α (精确到 1°);
i=1:3解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,由计算器可算得α≈22°.故斜坡CD的坡角α 为22°.解:分别过点B、C作BE⊥AD于E ,CF⊥AD于F ,
由题意可知BE=CF=23m , EF=BC=6m.在Rt△ABE中,(2) 坝底AD与斜坡AB的长度 (精确到0.1m). EFi=1:3在Rt△ABE中,由勾股定理可得在Rt△DCF中,同理可得故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.∴AD=AE+EF+FD=69+6+57.5=132.5(m)FD=2.5CF=2.5×23=57.5(m),EF解:作DE⊥AB于E , CF⊥AB于F ,
由题意可知DE=CF=4 (米),CD=EF=12 (米). 一段路基的横断面是梯形,高为 4 米,上底的宽是12 米,
路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽 (精确到0.1米, , ). ?
45°30°4米12米ABCD 在Rt△ADE中,EF
在Rt△BCF中,同理可得
因此 AB=AE+EF+BF≈4+12+6.93≈22.9 (米).
答: 路基下底的宽约为22.9米.(米).(米).解直角三角形的应用坡度问题方向角问题坡角坡度(或坡比) 课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
