五年级上册数学一课一练-7.折线统计图 青岛版(含解析)
文档属性
| 名称 | 五年级上册数学一课一练-7.折线统计图 青岛版(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 21:45:51 | ||
图片预览

文档简介
五年级上册数学一课一练-7.折线统计图
一、单选题
1.折线统计图表示( ???)。
A.?数量的多少和增减变化情况??????????????????B.?数量的多少??????????????????C.?部分量与总量的关系
2.宁宁从家出发去少年宫听讲座,当他走了大约一半路程时,想起忘了带门票.于是他回家取票,然后再去少年宫,听完报告后回家.下面(? )幅图比较准确地反映了宁宁的行为.
A.?B.?C.?
3.折线统计图可以清晰地表示出( )
A.?数量的多少??????B.?各部分数量与总量之间的关系??????C.?数量的增减变化情况??????D.?数据的分布情况
4.星期天,李老师带同学们乘汽车从学校出发去公园玩,在公园玩了2小时后乘车回学校,下面图(? )描述的是上面的叙述.
A.?????????B.?????????C.?
二、判断题
5.判断对错: 折线统计图可以清楚地表示出各部分同总数之间的关系.
6.条形统计图和折线统计图都可以看出数量的多少。
7.折线统计图不但可以表示出数量的多少,而且能清楚地表示出数量增减变化情况。
三、填空题
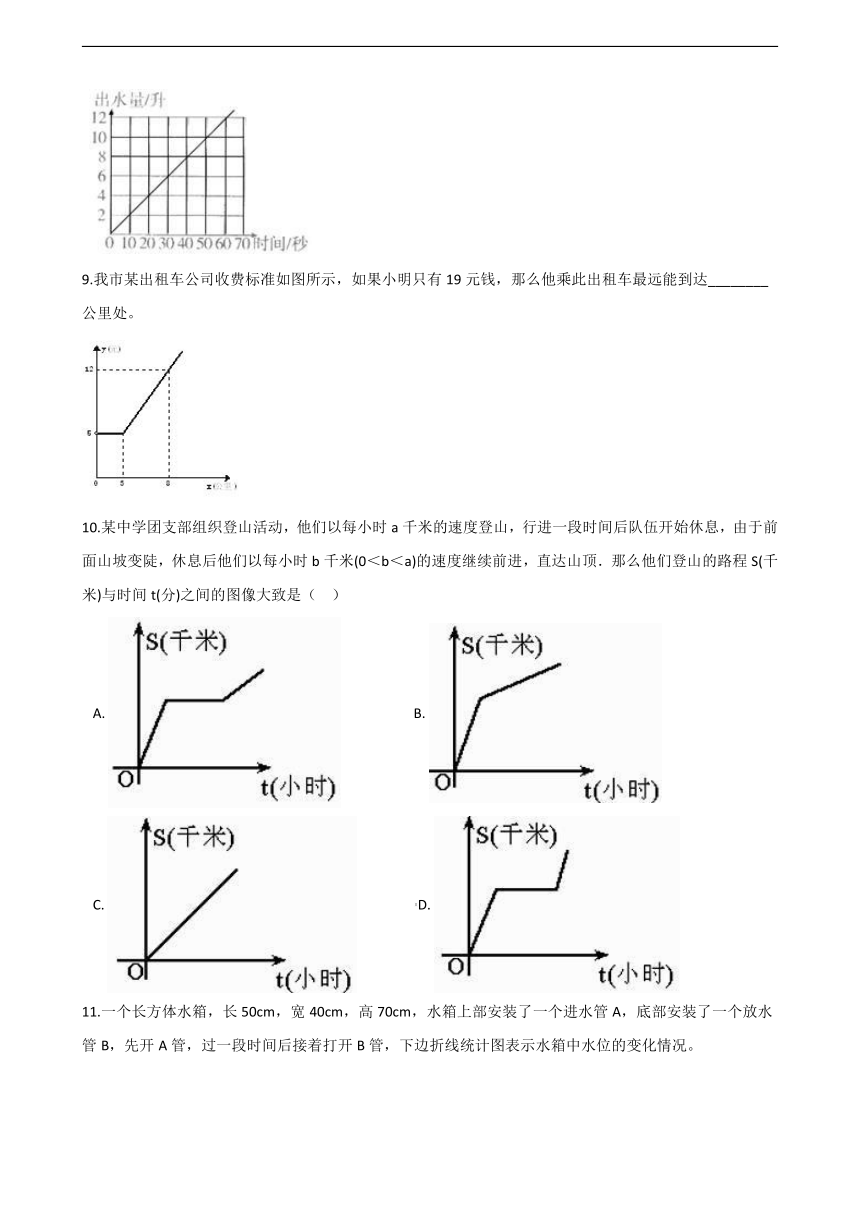
8.下图是一水龙头打开后的出水情况统计图,请根据统计图填空。
时间(秒)
30
________
出水量/升
________
9
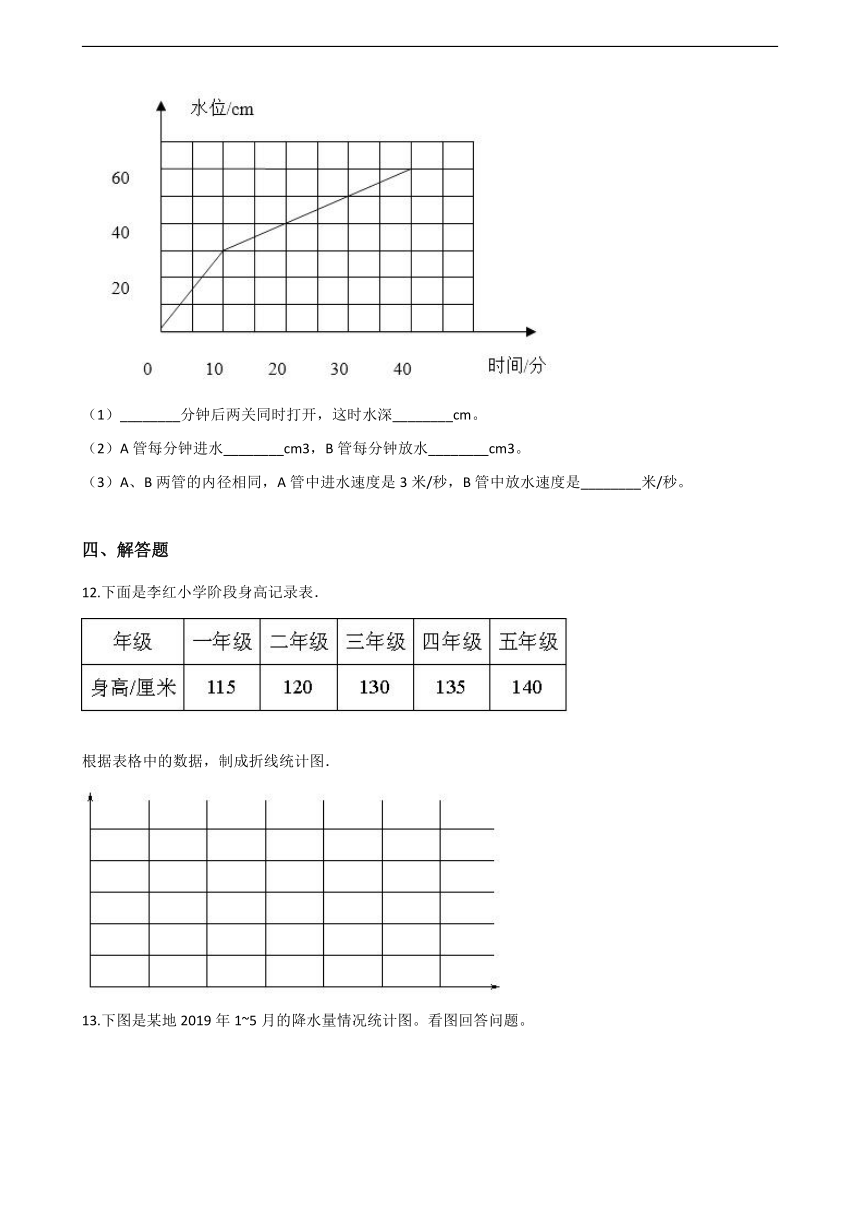
9.我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达________公里处。
10.某中学团支部组织登山活动,他们以每小时a千米的速度登山,行进一段时间后队伍开始休息,由于前面山坡变陡,休息后他们以每小时b千米(0<b<a)的速度继续前进,直达山顶.那么他们登山的路程S(千米)与时间t(分)之间的图像大致是(?? )
A.??????????????????????B.? C.??????????????????D.?
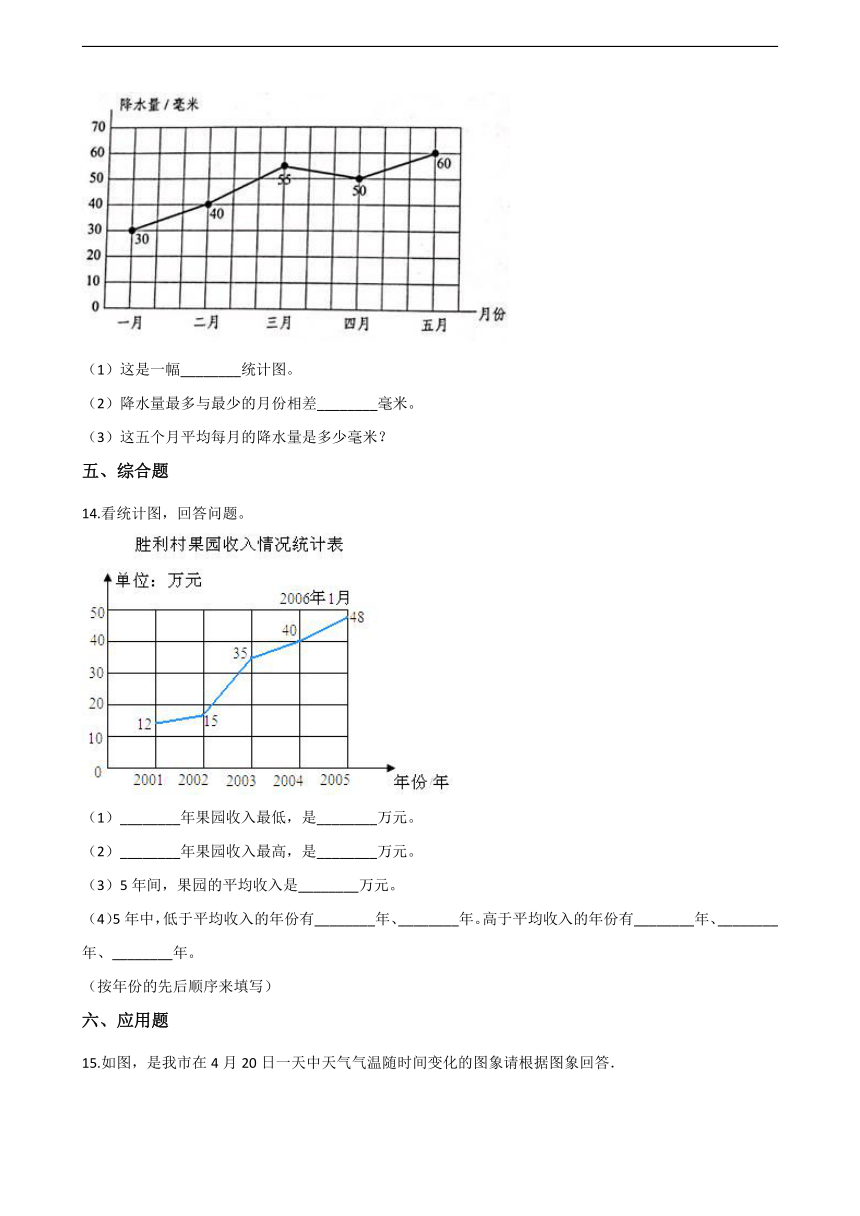
11.一个长方体水箱,长50cm,宽40cm,高70cm,水箱上部安装了一个进水管A,底部安装了一个放水管B,先开A管,过一段时间后接着打开B管,下边折线统计图表示水箱中水位的变化情况。
(1)________分钟后两关同时打开,这时水深________cm。
(2)A管每分钟进水________cm3,B管每分钟放水________cm3。
(3)A、B两管的内径相同,A管中进水速度是3米/秒,B管中放水速度是________米/秒。
四、解答题
12.下面是李红小学阶段身高记录表. 根据表格中的数据,制成折线统计图.
13.下图是某地2019年1~5月的降水量情况统计图。看图回答问题。
(1)这是一幅________统计图。
(2)降水量最多与最少的月份相差________毫米。
(3)这五个月平均每月的降水量是多少毫米?
五、综合题
14.看统计图,回答问题。
(1)________年果园收入最低,是________万元。
(2)________年果园收入最高,是________万元。
(3)5年间,果园的平均收入是________万元。
(4)5年中,低于平均收入的年份有________年、________年。高于平均收入的年份有________年、________年、________年。
(按年份的先后顺序来填写)
六、应用题
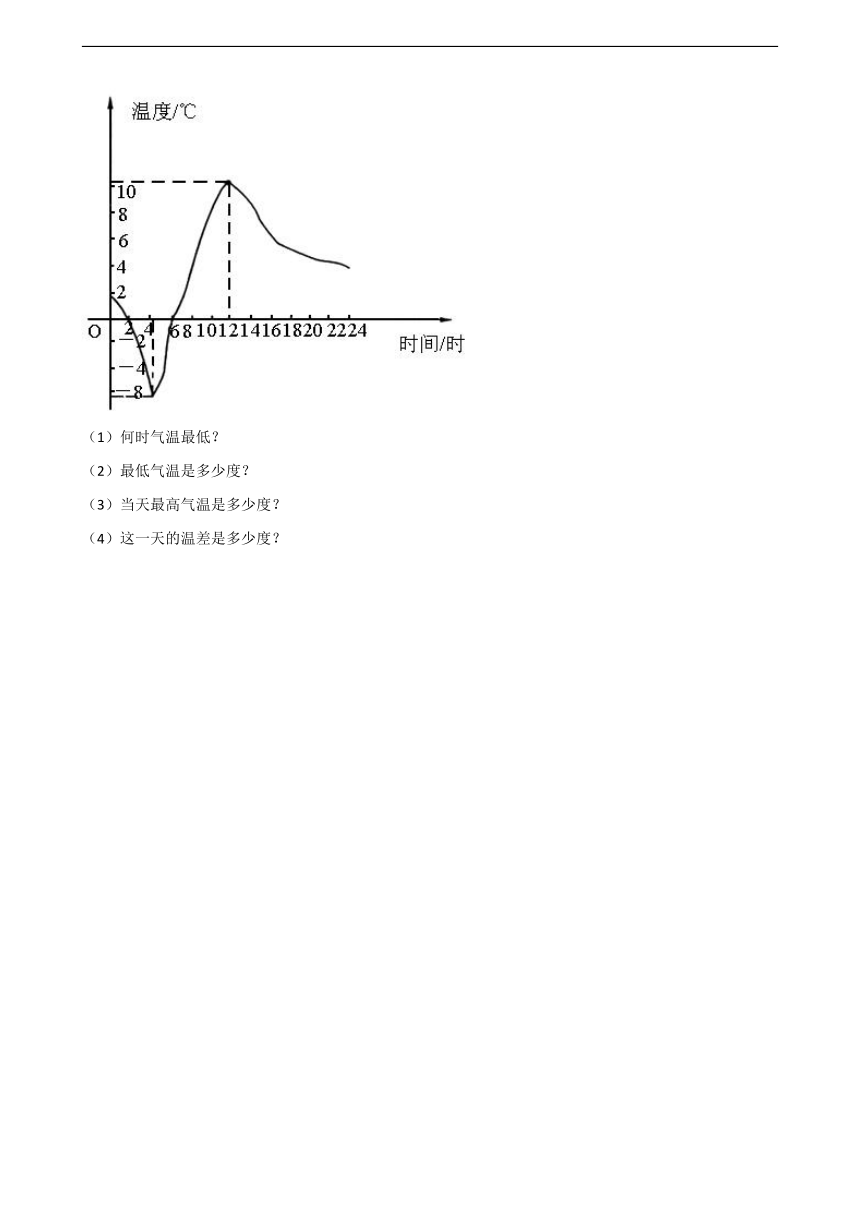
15.如图,是我市在4月20日一天中天气气温随时间变化的图象请根据图象回答.
(1)何时气温最低?
(2)最低气温是多少度?
(3)当天最高气温是多少度?
(4)这一天的温差是多少度?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】解:折线统计图表示数量的多少和增减变化情况。 故答案为:A。
【分析】条形统计图表示数量的多少;折线统计图不仅表示数量的多少还表示数量的增减变化情况;扇形统计图表示部分与总量之间的关系。
2.【答案】 C
【解析】【解答】符合宁宁这段时间离家距离变化的是C。
【分析】离家的距离是随时间是这样变化的:(1)先离家越来远,到了最远距离一半的时候;(2)然后越来越近直到为0;(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;(4)然后再离家越来越远,直到少年宫;(5)在少年宫听报告还要一段时间,所以离家最远的时候也是一条线段;(6)然后回家直到离家的距离为0。
故选:C
3.【答案】 C
【解析】【解答】解:根据三种统计图的特点可知:
条形统计图能清楚的表示出数量的多少;
折线统计图可以清晰地表示出数量的多少,而且能看出各种数量的增减变化情况.
扇形统计图表示各部分数量与总量之间的关系及数据的分布情况.
故选:C.
【分析】条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图的特点:比较清楚地反映出部分与部分、部分与整体之间的数量关系;据此解答即可.
4.【答案】A
【解析】【解答】解:由折线统计图A所提供的信息与题中所提供的信息相同;
故选:A.
【分析】折线统计图A提供的信息是从学校出发去公园玩,在公园玩了2小时后乘车回学校;由折线统计图B所提供的信息是从公园回到学校,在学校呆了一段时间后,又从学校出去到了某地;由折线统计图C所提供的信息是从公园回到学校,又从学校出去到了某地;据此解答.此题主要考查的是如何观察折线统计图并从图中获取信息.
二、判断题
5.【答案】错误
【解析】【解答】解:折线统计图主要是反映数据的大小及数据增减变化的.
6.【答案】 正确
【解析】【解答】解:条形统计图和折线统计图都可以看出数量的多少。原题说法正确。 故答案为:正确。 【分析】条形统计图能清楚地表示数量的多少,折线统计图不仅能表示数量的多少还能表示数量的增减变化情况。
7.【答案】 正确
【解析】【解答】解:折线统计图能表示出数量的多少,还能根据折线的走势表示出数量增减变化情况,原题说法正确. 故答案为:正确
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示出数量的多少,还能表示出数量的增减变化情况;扇形统计图能表示出部分与整体之间的关系;由此判断即可.
三、填空题
8.【答案】 45;6
【解析】【解答】解:2÷10=0.2(升); 30×0.2=6(升); 9÷0.2=45(秒); 故表格为:
【分析】观察折线统计图,横轴表示时间,竖轴表示出水量,根据折线对应在横轴和竖轴上的数据可知,水龙头打开30秒的出水量是6升,出水量是9升时的时间应为45秒,据此填入表格即可。
9.【答案】12
【解析】【解答】(12-6)÷(8-5) =6÷3 =2(元) (19-5)÷2=7(公里) 5+7=12(公里) 所以,他乘此出租车最远能到达12公里处。 【分析】本题考查的是折线统计图的分析与计算,关键是求出超出部分每公里的钱数。
10.【答案】 A
【解析】【解答】根据题意,登山运动分为三个阶段,快行、停止、慢行,反应到图象上是:三条线段陡,平,缓.
故答案为:A.
【分析】根据题意可知,登山路程随着时间的增多是在不断增多,由于速度的变化形式为大,0,小,所以随着时间的变化,路程的函数图象也将表现为:陡,平,缓.
11.【答案】(1)10 ;30 (2)6000 ;4000 (3)2
【解析】【解答】解:(1)根据图像判断,10分钟后两关同时打开,这时水深30米; (2)A管每分钟进水:30÷10=3(厘米);50×40×3=6000(立方厘米) B管每分钟放水: (3×40-60)÷(40-10) =60÷30 =2(厘米) 50×40×2=4000(立方厘米) (3)进水速度与放水速度的比是6000:4000=3:2,所以B管中放水速度是2米/秒. 故答案为:10,30;6000,4000;2
【分析】(1)根据折线的走势直接判断两关同时开的时间,从对应的刻度中找出水深;(2)用两关同时开时的水位高度除以时间求出A管每分钟进水的高度,然后用底面积乘高度求出每分钟的进水量;用40分钟进水的高度减去此时水面的高度即可求出每分钟放水的高度,然后用底面积乘这个高度即可求出每分钟放水的体积;(3)写出进水与放水的速度比,然后判断放水速度是多少即可.
四、解答题
12.【答案】解:统计图如下:
【解析】【分析】横轴表示年级,竖轴表示身高,根据统计表中的数据先判断出各点的位置,再描出各点,然后用线段顺次连接各点即可绘制出折线统计图.
13.【答案】 (1)折线 (2)30 (3)(30+40+55+50+60)÷5 =235÷5 =47(毫米) 答:这五个月平均每月的降水量是47毫米。
【解析】【解答】解:(1)看图可知,这是一幅折线统计图; (2)降水量最多与最少的月份相差60-30=30(毫米); 故答案为:(1)折线;(2)30。 【分析】(1)观察统计图的特征确定统计图的类型; (2)最多的是60毫米,最少的是30毫米,用减法计算相差的毫米数即可; (3)用这五个月降水量的和除以5即可求出平均每月的降水量。
五、综合题
14.【答案】 (1)2001;12 (2)2005;48 (3)30 (4)2001;2002;2003;2004;2005
【解析】【解答】(1)2001年果园收入最低,是12万元。 (2)2005年果园收入最高,是48万元。 (3)(12+15+35+40+48)÷5=30(万元) (4)5年中,低于平均收入的年份有2001年、2002年。高于平均收入的年份有2003年、2004年、2005年。
【分析】从折线统计图中获取信息,并解答问题。
六、应用题
15.【答案】(1)4点
(2)-8℃
(3)10℃
(4)18度
【解析】【分析】根据折线的高低决定气温的高低.
一、单选题
1.折线统计图表示( ???)。
A.?数量的多少和增减变化情况??????????????????B.?数量的多少??????????????????C.?部分量与总量的关系
2.宁宁从家出发去少年宫听讲座,当他走了大约一半路程时,想起忘了带门票.于是他回家取票,然后再去少年宫,听完报告后回家.下面(? )幅图比较准确地反映了宁宁的行为.
A.?B.?C.?
3.折线统计图可以清晰地表示出( )
A.?数量的多少??????B.?各部分数量与总量之间的关系??????C.?数量的增减变化情况??????D.?数据的分布情况
4.星期天,李老师带同学们乘汽车从学校出发去公园玩,在公园玩了2小时后乘车回学校,下面图(? )描述的是上面的叙述.
A.?????????B.?????????C.?
二、判断题
5.判断对错: 折线统计图可以清楚地表示出各部分同总数之间的关系.
6.条形统计图和折线统计图都可以看出数量的多少。
7.折线统计图不但可以表示出数量的多少,而且能清楚地表示出数量增减变化情况。
三、填空题
8.下图是一水龙头打开后的出水情况统计图,请根据统计图填空。
时间(秒)
30
________
出水量/升
________
9
9.我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达________公里处。
10.某中学团支部组织登山活动,他们以每小时a千米的速度登山,行进一段时间后队伍开始休息,由于前面山坡变陡,休息后他们以每小时b千米(0<b<a)的速度继续前进,直达山顶.那么他们登山的路程S(千米)与时间t(分)之间的图像大致是(?? )
A.??????????????????????B.? C.??????????????????D.?
11.一个长方体水箱,长50cm,宽40cm,高70cm,水箱上部安装了一个进水管A,底部安装了一个放水管B,先开A管,过一段时间后接着打开B管,下边折线统计图表示水箱中水位的变化情况。
(1)________分钟后两关同时打开,这时水深________cm。
(2)A管每分钟进水________cm3,B管每分钟放水________cm3。
(3)A、B两管的内径相同,A管中进水速度是3米/秒,B管中放水速度是________米/秒。
四、解答题
12.下面是李红小学阶段身高记录表. 根据表格中的数据,制成折线统计图.
13.下图是某地2019年1~5月的降水量情况统计图。看图回答问题。
(1)这是一幅________统计图。
(2)降水量最多与最少的月份相差________毫米。
(3)这五个月平均每月的降水量是多少毫米?
五、综合题
14.看统计图,回答问题。
(1)________年果园收入最低,是________万元。
(2)________年果园收入最高,是________万元。
(3)5年间,果园的平均收入是________万元。
(4)5年中,低于平均收入的年份有________年、________年。高于平均收入的年份有________年、________年、________年。
(按年份的先后顺序来填写)
六、应用题
15.如图,是我市在4月20日一天中天气气温随时间变化的图象请根据图象回答.
(1)何时气温最低?
(2)最低气温是多少度?
(3)当天最高气温是多少度?
(4)这一天的温差是多少度?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】解:折线统计图表示数量的多少和增减变化情况。 故答案为:A。
【分析】条形统计图表示数量的多少;折线统计图不仅表示数量的多少还表示数量的增减变化情况;扇形统计图表示部分与总量之间的关系。
2.【答案】 C
【解析】【解答】符合宁宁这段时间离家距离变化的是C。
【分析】离家的距离是随时间是这样变化的:(1)先离家越来远,到了最远距离一半的时候;(2)然后越来越近直到为0;(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;(4)然后再离家越来越远,直到少年宫;(5)在少年宫听报告还要一段时间,所以离家最远的时候也是一条线段;(6)然后回家直到离家的距离为0。
故选:C
3.【答案】 C
【解析】【解答】解:根据三种统计图的特点可知:
条形统计图能清楚的表示出数量的多少;
折线统计图可以清晰地表示出数量的多少,而且能看出各种数量的增减变化情况.
扇形统计图表示各部分数量与总量之间的关系及数据的分布情况.
故选:C.
【分析】条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图的特点:比较清楚地反映出部分与部分、部分与整体之间的数量关系;据此解答即可.
4.【答案】A
【解析】【解答】解:由折线统计图A所提供的信息与题中所提供的信息相同;
故选:A.
【分析】折线统计图A提供的信息是从学校出发去公园玩,在公园玩了2小时后乘车回学校;由折线统计图B所提供的信息是从公园回到学校,在学校呆了一段时间后,又从学校出去到了某地;由折线统计图C所提供的信息是从公园回到学校,又从学校出去到了某地;据此解答.此题主要考查的是如何观察折线统计图并从图中获取信息.
二、判断题
5.【答案】错误
【解析】【解答】解:折线统计图主要是反映数据的大小及数据增减变化的.
6.【答案】 正确
【解析】【解答】解:条形统计图和折线统计图都可以看出数量的多少。原题说法正确。 故答案为:正确。 【分析】条形统计图能清楚地表示数量的多少,折线统计图不仅能表示数量的多少还能表示数量的增减变化情况。
7.【答案】 正确
【解析】【解答】解:折线统计图能表示出数量的多少,还能根据折线的走势表示出数量增减变化情况,原题说法正确. 故答案为:正确
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示出数量的多少,还能表示出数量的增减变化情况;扇形统计图能表示出部分与整体之间的关系;由此判断即可.
三、填空题
8.【答案】 45;6
【解析】【解答】解:2÷10=0.2(升); 30×0.2=6(升); 9÷0.2=45(秒); 故表格为:
【分析】观察折线统计图,横轴表示时间,竖轴表示出水量,根据折线对应在横轴和竖轴上的数据可知,水龙头打开30秒的出水量是6升,出水量是9升时的时间应为45秒,据此填入表格即可。
9.【答案】12
【解析】【解答】(12-6)÷(8-5) =6÷3 =2(元) (19-5)÷2=7(公里) 5+7=12(公里) 所以,他乘此出租车最远能到达12公里处。 【分析】本题考查的是折线统计图的分析与计算,关键是求出超出部分每公里的钱数。
10.【答案】 A
【解析】【解答】根据题意,登山运动分为三个阶段,快行、停止、慢行,反应到图象上是:三条线段陡,平,缓.
故答案为:A.
【分析】根据题意可知,登山路程随着时间的增多是在不断增多,由于速度的变化形式为大,0,小,所以随着时间的变化,路程的函数图象也将表现为:陡,平,缓.
11.【答案】(1)10 ;30 (2)6000 ;4000 (3)2
【解析】【解答】解:(1)根据图像判断,10分钟后两关同时打开,这时水深30米; (2)A管每分钟进水:30÷10=3(厘米);50×40×3=6000(立方厘米) B管每分钟放水: (3×40-60)÷(40-10) =60÷30 =2(厘米) 50×40×2=4000(立方厘米) (3)进水速度与放水速度的比是6000:4000=3:2,所以B管中放水速度是2米/秒. 故答案为:10,30;6000,4000;2
【分析】(1)根据折线的走势直接判断两关同时开的时间,从对应的刻度中找出水深;(2)用两关同时开时的水位高度除以时间求出A管每分钟进水的高度,然后用底面积乘高度求出每分钟的进水量;用40分钟进水的高度减去此时水面的高度即可求出每分钟放水的高度,然后用底面积乘这个高度即可求出每分钟放水的体积;(3)写出进水与放水的速度比,然后判断放水速度是多少即可.
四、解答题
12.【答案】解:统计图如下:
【解析】【分析】横轴表示年级,竖轴表示身高,根据统计表中的数据先判断出各点的位置,再描出各点,然后用线段顺次连接各点即可绘制出折线统计图.
13.【答案】 (1)折线 (2)30 (3)(30+40+55+50+60)÷5 =235÷5 =47(毫米) 答:这五个月平均每月的降水量是47毫米。
【解析】【解答】解:(1)看图可知,这是一幅折线统计图; (2)降水量最多与最少的月份相差60-30=30(毫米); 故答案为:(1)折线;(2)30。 【分析】(1)观察统计图的特征确定统计图的类型; (2)最多的是60毫米,最少的是30毫米,用减法计算相差的毫米数即可; (3)用这五个月降水量的和除以5即可求出平均每月的降水量。
五、综合题
14.【答案】 (1)2001;12 (2)2005;48 (3)30 (4)2001;2002;2003;2004;2005
【解析】【解答】(1)2001年果园收入最低,是12万元。 (2)2005年果园收入最高,是48万元。 (3)(12+15+35+40+48)÷5=30(万元) (4)5年中,低于平均收入的年份有2001年、2002年。高于平均收入的年份有2003年、2004年、2005年。
【分析】从折线统计图中获取信息,并解答问题。
六、应用题
15.【答案】(1)4点
(2)-8℃
(3)10℃
(4)18度
【解析】【分析】根据折线的高低决定气温的高低.
