北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第14讲 全等三角形判定一(提高)含答案
文档属性
| 名称 | 北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第14讲 全等三角形判定一(提高)含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 00:00:00 | ||
图片预览


文档简介
全等三角形判定一(SSS,ASA,AAS)(提高)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,判定方法2——“角边角”,判定方法3——“角角边”;能运用它们判定两个三角形全等.
2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果/=AB,/=AC,/=BC,则△ABC≌△/.
/
要点二、全等三角形判定2——“角边角”
全等三角形判定2——“角边角”
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
要点诠释:如图,如果∠A=∠/,AB=/,∠B=∠/,则△ABC≌△/.
/
要点三、全等三角形判定3——“角角边”
1.全等三角形判定3——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.
/
要点四、如何选择三角形证全等
1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
2.可以从已知出发,看已知条件确定证哪两个三角形全等;
3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
4.如果以上方法都行不通,就添加辅助线,构造全等三角形.
【典型例题】
类型一、全等三角形的判定1——“边边边”
/1、如图,在△ABC和△ADE中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.
/
【答案与解析】
证明:在△ABD和△ACE中,
/
∴△ABD≌△ACE(SSS)
∴∠BAD=∠CAE(全等三角形对应角相等).
【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD=∠CAE,先找出这两个角所在的三角形分别是△BDA和△CAE,然后证这两个三角形全等.
举一反三:
【变式】(2019秋?双峰县校级期中)如图,已知AB=DC,若要用“SSS”判定△ABC≌△DCB,应添加条件是 .
/
【答案】AC=DB.
类型二、全等三角形的判定2——“角边角”
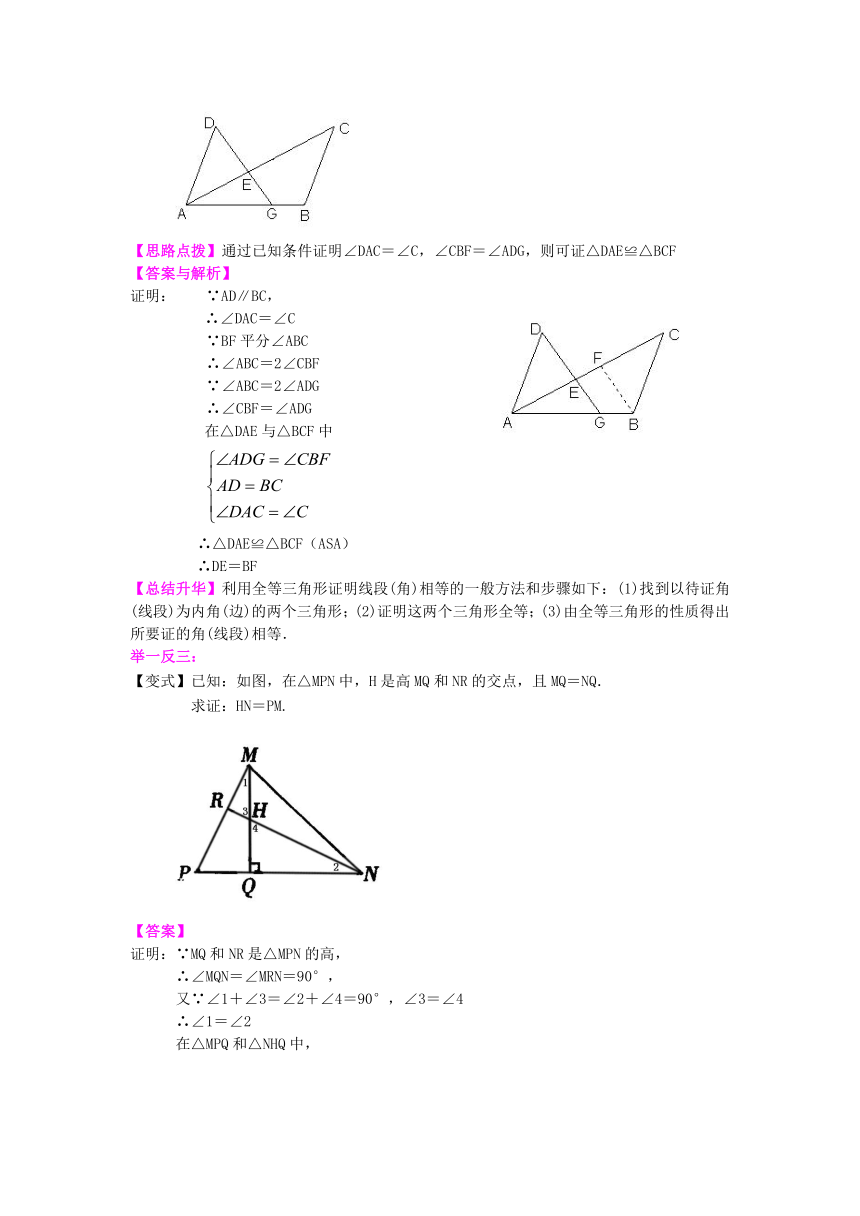
/2、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
/
【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF
【答案与解析】
证明: ∵AD∥BC,
∴∠DAC=∠C
∵BF平分∠ABC
∴∠ABC=2∠CBF
∵∠ABC=2∠ADG
∴∠CBF=∠ADG
在△DAE与△BCF中
/
∴△DAE≌△BCF(ASA)
∴DE=BF
【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.
举一反三:
【变式】已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.
求证:HN=PM.
/
【答案】
证明:∵MQ和NR是△MPN的高,
∴∠MQN=∠MRN=90°,
又∵∠1+∠3=∠2+∠4=90°,∠3=∠4
∴∠1=∠2
在△MPQ和△NHQ中,
/
∴△MPQ≌△NHQ(ASA)
∴PM=HN
类型三、全等三角形的判定3——“角角边”
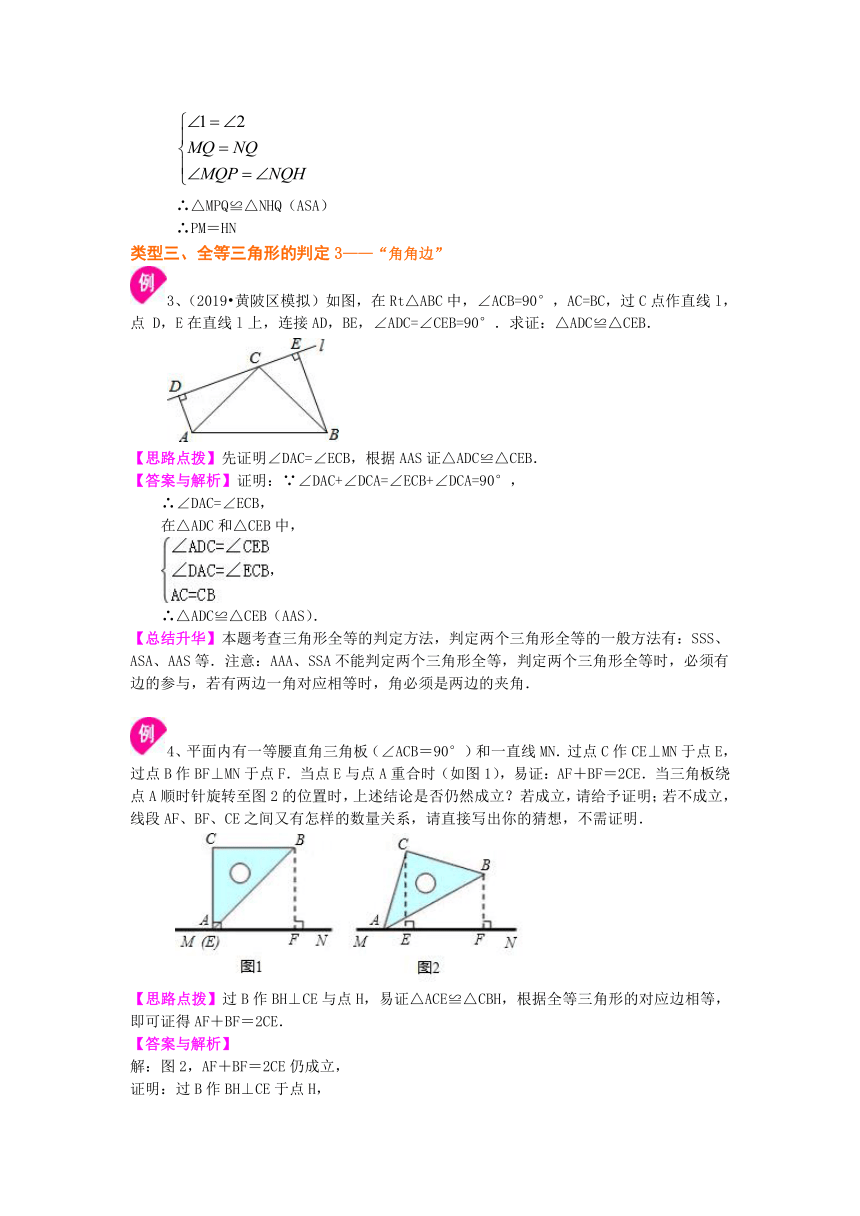
/3、(2019?黄陂区模拟)如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
/
【思路点拨】先证明∠DAC=∠ECB,根据AAS证△ADC≌△CEB.
【答案与解析】证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
/,
∴△ADC≌△CEB(AAS).
【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、ASA、AAS等.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
/4、平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
/
【思路点拨】过B作BH⊥CE与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.
【答案与解析】
解:图2,AF+BF=2CE仍成立,
证明:过B作BH⊥CE于点H,
∵∠CBH+∠BCH=∠ACE+∠BCH=90°
∴∠CBH=∠ACE
在△ACE与△CBH中,
/
∴△ACE≌△CBH.(AAS)
∴CH=AE,BF=HE,CE=EF,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
/
【总结升华】正确作出垂线,构造全等三角形是解决本题的关键.
举一反三:
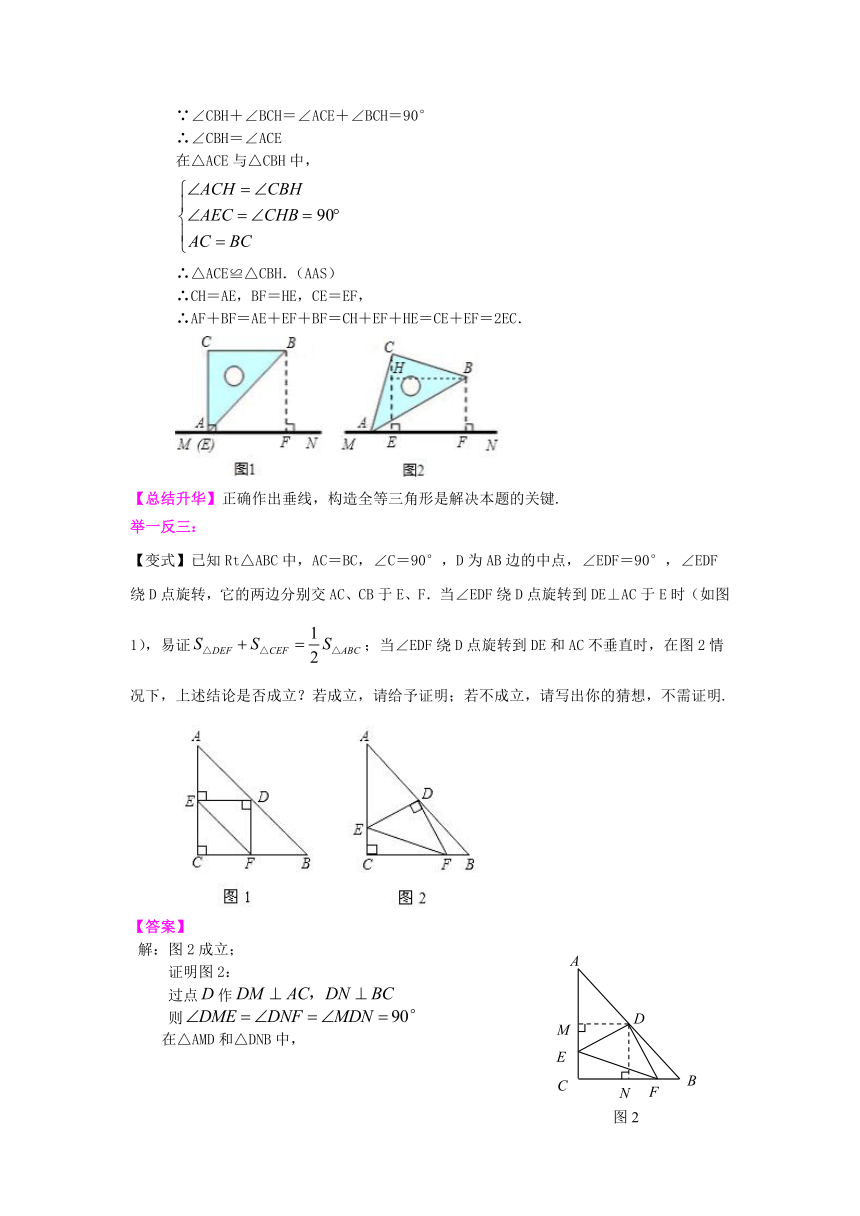
【变式】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证/;当∠EDF绕D点旋转到DE和AC不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.
/
【答案】
解:图2成立;
证明图2:
过点/作/
则/
在△AMD和△DNB中,
/
∴△AMD≌△DNB(AAS)
∴DM=DN
∵∠MDE+∠EDN=∠NDF+∠EDN=90°,
∴∠ MDE=∠NDF
在△DME与△DNF中,
/
∴△DME≌△DNF(ASA)
∴/
∴/
可知/,
∴/
类型四、全等三角形判定的实际应用
/5、(2019春?龙岗区期末)小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米? /
【思路点拨】根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB﹣PB求出即可. 【答案与解析】 解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°, ∴∠DCP=∠APB=54°, 在△CPD和△PAB中 ∵/, ∴△CPD≌△PAB(ASA), ∴DP=AB, ∵DB=36,PB=10, ∴AB=36﹣10=26(m), 答:楼高AB是26米. 【总结升华】此题主要考查了全等三角形的应用,根据题意得出△CPD≌△PAB是解题关键.
【巩固练习】
一、选择题
1.(2019秋?西秀区校级期末)如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
/
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
2. 如图,AB∥EF,DE∥AC,BD=CF,则图中不是全等三角形的是( )
A.△BAC≌FED B. △BDA≌FCE C. △DEC≌CAD D. △BAC≌FCE
/
3. 如图,AB=BD,∠1=∠2,添加一个条件可使△ABC≌△DBE,则这个条件不可能是( )
A.AE=EC B.∠D=∠A C.BE=BC D.∠1=∠DEA
/
4. 下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
5. △ABC和△/中, 条件 ①AB =/, ②BC =/, ③ AC=/, ④ ∠A = ∠/, ⑤ ∠B = ∠/, ⑥ ∠C = ∠/, 则下列各组条件中, 不能保证△ABC≌△/的是( )
A.①②③ B. ①②⑤ C. ①③⑤ D. ②⑤⑥
6.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC B.BC C.AB D.AE+AC
/
二、填空题
7. 已知:如图,AE=DF,∠A=∠D,欲证ΔACE≌ΔDBF,判定定理为AAS,需要添加条件______;或添加条件______,证明全等的理由是ASA.
/
8.(2019秋?白云区期末)如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是__________.
/
9.(2019?滨湖区一模)如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 ,使△ABC≌△DEF.
/
10. 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.
/
11.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则EF的长是___________.
/
12. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.
/
三、解答题
13.(2019春?会宁县期中)已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB.
/
14. 已知:如图,/中,/,/于/,/于/,/与/相交于点/.求证:/.
/
15.(2019秋?杭州期末)如图,DC∥AB,∠BAD和∠ADC的角平分线相交于E,过E的直线分别交DC、AB于C、B两点.求证:AD=AB+DC.
/
【答案与解析】
一、选择题
1. 【答案】B.
2. 【答案】D;
3. 【答案】A;
【解析】D选项可证得∠D=∠A,从而用ASA证全等.
4. 【答案】B;
【解析】C选项和D选项都可以由SSS定理证全等.
5. 【答案】C;
【解析】C选项是两边及一边的对角对应相等,不能保证全等.
6. 【答案】C;
【解析】可证∠BAC=∠E,∠BCA=∠DCE,所以△ABC≌△EDC,DE=AB.
二、填空题
7. 【答案】∠2=∠1;∠E=∠F.
8. 【答案】AAS;
9. 【答案】∠A=∠D或∠ACB=∠F;
【解析】解:可添加条件为∠A=∠D或∠ACB=∠F.
理由如下:∵AB∥DE,
∴∠B=∠DEF.
∵在△ABC和△DEF中,
/,
∴△ABC≌△DEF(ASA).
故答案是:∠A=∠D或∠ACB=∠F.
10.【答案】6;
【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.
11.【答案】3;
【解析】由AAS证△ABF≌△CBE,EF=FB+BE=CE+AF=2+1=3.
12.【答案】66°;
【解析】可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=/,所以∠DCB=
∠ABC=25°+41°=66°
三、解答题
13.【解析】
证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
/,
∴△ADC≌△CEB(AAS).
14.【解析】
证明: ∵ /
∴ /
∵ /
∴ /
∴ /
∵ /
∴ /
∴ /
∵ /
∴ /
∴ /
在/和/中
/
∴/≌/ (AAS)
∴/
15.【解析】
证明:延长DE交AB的延长线于F
∴∠CDE=∠F, ∠CDA+∠BAD=180o
∵DE平分∠CDA,AE平分∠DAB
∴∠CDE=∠ADE=/∠CDA,
∠DAE=∠EAF=/∠BAD
∴∠ADE=∠F,∠EDA+∠DAE=90o
∴∠AED=∠AEF=90o
在△ADE与△AFE中
/
∴△ADE≌△AFE (AAS)
∴DE=EF,AD=AF
在△DCE与△FBE中
/
∴△DCE≌△FBE (ASA)
∴DC=BF
∴AD=AB+DC.
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,判定方法2——“角边角”,判定方法3——“角角边”;能运用它们判定两个三角形全等.
2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果/=AB,/=AC,/=BC,则△ABC≌△/.
/
要点二、全等三角形判定2——“角边角”
全等三角形判定2——“角边角”
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
要点诠释:如图,如果∠A=∠/,AB=/,∠B=∠/,则△ABC≌△/.
/
要点三、全等三角形判定3——“角角边”
1.全等三角形判定3——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.
/
要点四、如何选择三角形证全等
1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
2.可以从已知出发,看已知条件确定证哪两个三角形全等;
3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
4.如果以上方法都行不通,就添加辅助线,构造全等三角形.
【典型例题】
类型一、全等三角形的判定1——“边边边”
/1、如图,在△ABC和△ADE中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.
/
【答案与解析】
证明:在△ABD和△ACE中,
/
∴△ABD≌△ACE(SSS)
∴∠BAD=∠CAE(全等三角形对应角相等).
【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD=∠CAE,先找出这两个角所在的三角形分别是△BDA和△CAE,然后证这两个三角形全等.
举一反三:
【变式】(2019秋?双峰县校级期中)如图,已知AB=DC,若要用“SSS”判定△ABC≌△DCB,应添加条件是 .
/
【答案】AC=DB.
类型二、全等三角形的判定2——“角边角”
/2、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
/
【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF
【答案与解析】
证明: ∵AD∥BC,
∴∠DAC=∠C
∵BF平分∠ABC
∴∠ABC=2∠CBF
∵∠ABC=2∠ADG
∴∠CBF=∠ADG
在△DAE与△BCF中
/
∴△DAE≌△BCF(ASA)
∴DE=BF
【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.
举一反三:
【变式】已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.
求证:HN=PM.
/
【答案】
证明:∵MQ和NR是△MPN的高,
∴∠MQN=∠MRN=90°,
又∵∠1+∠3=∠2+∠4=90°,∠3=∠4
∴∠1=∠2
在△MPQ和△NHQ中,
/
∴△MPQ≌△NHQ(ASA)
∴PM=HN
类型三、全等三角形的判定3——“角角边”
/3、(2019?黄陂区模拟)如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
/
【思路点拨】先证明∠DAC=∠ECB,根据AAS证△ADC≌△CEB.
【答案与解析】证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
/,
∴△ADC≌△CEB(AAS).
【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、ASA、AAS等.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
/4、平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
/
【思路点拨】过B作BH⊥CE与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.
【答案与解析】
解:图2,AF+BF=2CE仍成立,
证明:过B作BH⊥CE于点H,
∵∠CBH+∠BCH=∠ACE+∠BCH=90°
∴∠CBH=∠ACE
在△ACE与△CBH中,
/
∴△ACE≌△CBH.(AAS)
∴CH=AE,BF=HE,CE=EF,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
/
【总结升华】正确作出垂线,构造全等三角形是解决本题的关键.
举一反三:
【变式】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证/;当∠EDF绕D点旋转到DE和AC不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.
/
【答案】
解:图2成立;
证明图2:
过点/作/
则/
在△AMD和△DNB中,
/
∴△AMD≌△DNB(AAS)
∴DM=DN
∵∠MDE+∠EDN=∠NDF+∠EDN=90°,
∴∠ MDE=∠NDF
在△DME与△DNF中,
/
∴△DME≌△DNF(ASA)
∴/
∴/
可知/,
∴/
类型四、全等三角形判定的实际应用
/5、(2019春?龙岗区期末)小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米? /
【思路点拨】根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB﹣PB求出即可. 【答案与解析】 解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°, ∴∠DCP=∠APB=54°, 在△CPD和△PAB中 ∵/, ∴△CPD≌△PAB(ASA), ∴DP=AB, ∵DB=36,PB=10, ∴AB=36﹣10=26(m), 答:楼高AB是26米. 【总结升华】此题主要考查了全等三角形的应用,根据题意得出△CPD≌△PAB是解题关键.
【巩固练习】
一、选择题
1.(2019秋?西秀区校级期末)如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
/
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
2. 如图,AB∥EF,DE∥AC,BD=CF,则图中不是全等三角形的是( )
A.△BAC≌FED B. △BDA≌FCE C. △DEC≌CAD D. △BAC≌FCE
/
3. 如图,AB=BD,∠1=∠2,添加一个条件可使△ABC≌△DBE,则这个条件不可能是( )
A.AE=EC B.∠D=∠A C.BE=BC D.∠1=∠DEA
/
4. 下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
5. △ABC和△/中, 条件 ①AB =/, ②BC =/, ③ AC=/, ④ ∠A = ∠/, ⑤ ∠B = ∠/, ⑥ ∠C = ∠/, 则下列各组条件中, 不能保证△ABC≌△/的是( )
A.①②③ B. ①②⑤ C. ①③⑤ D. ②⑤⑥
6.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC B.BC C.AB D.AE+AC
/
二、填空题
7. 已知:如图,AE=DF,∠A=∠D,欲证ΔACE≌ΔDBF,判定定理为AAS,需要添加条件______;或添加条件______,证明全等的理由是ASA.
/
8.(2019秋?白云区期末)如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是__________.
/
9.(2019?滨湖区一模)如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 ,使△ABC≌△DEF.
/
10. 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.
/
11.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则EF的长是___________.
/
12. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.
/
三、解答题
13.(2019春?会宁县期中)已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB.
/
14. 已知:如图,/中,/,/于/,/于/,/与/相交于点/.求证:/.
/
15.(2019秋?杭州期末)如图,DC∥AB,∠BAD和∠ADC的角平分线相交于E,过E的直线分别交DC、AB于C、B两点.求证:AD=AB+DC.
/
【答案与解析】
一、选择题
1. 【答案】B.
2. 【答案】D;
3. 【答案】A;
【解析】D选项可证得∠D=∠A,从而用ASA证全等.
4. 【答案】B;
【解析】C选项和D选项都可以由SSS定理证全等.
5. 【答案】C;
【解析】C选项是两边及一边的对角对应相等,不能保证全等.
6. 【答案】C;
【解析】可证∠BAC=∠E,∠BCA=∠DCE,所以△ABC≌△EDC,DE=AB.
二、填空题
7. 【答案】∠2=∠1;∠E=∠F.
8. 【答案】AAS;
9. 【答案】∠A=∠D或∠ACB=∠F;
【解析】解:可添加条件为∠A=∠D或∠ACB=∠F.
理由如下:∵AB∥DE,
∴∠B=∠DEF.
∵在△ABC和△DEF中,
/,
∴△ABC≌△DEF(ASA).
故答案是:∠A=∠D或∠ACB=∠F.
10.【答案】6;
【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.
11.【答案】3;
【解析】由AAS证△ABF≌△CBE,EF=FB+BE=CE+AF=2+1=3.
12.【答案】66°;
【解析】可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=/,所以∠DCB=
∠ABC=25°+41°=66°
三、解答题
13.【解析】
证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
/,
∴△ADC≌△CEB(AAS).
14.【解析】
证明: ∵ /
∴ /
∵ /
∴ /
∴ /
∵ /
∴ /
∴ /
∵ /
∴ /
∴ /
在/和/中
/
∴/≌/ (AAS)
∴/
15.【解析】
证明:延长DE交AB的延长线于F
∴∠CDE=∠F, ∠CDA+∠BAD=180o
∵DE平分∠CDA,AE平分∠DAB
∴∠CDE=∠ADE=/∠CDA,
∠DAE=∠EAF=/∠BAD
∴∠ADE=∠F,∠EDA+∠DAE=90o
∴∠AED=∠AEF=90o
在△ADE与△AFE中
/
∴△ADE≌△AFE (AAS)
∴DE=EF,AD=AF
在△DCE与△FBE中
/
∴△DCE≌△FBE (ASA)
∴DC=BF
∴AD=AB+DC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
