北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第21讲《生活中的轴对称》全章复习与巩固(提高)
文档属性
| 名称 | 北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第21讲《生活中的轴对称》全章复习与巩固(提高) |  | |
| 格式 | zip | ||
| 文件大小 | 398.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-10 13:36:23 | ||
图片预览



文档简介
《生活中的轴对称》全章复习与巩固(提高)
【学习目标】
1.认识和欣赏身边的轴对称图形,增进学习数学的兴趣.
2.了解轴对称的概念,探索轴对称、轴对称图形的基本性质及它们的简单应用.
3.探索线段的垂直平分线、角平分线和等腰三角形的性质以及判定方法.
4.能按照要求,画出一些轴对称图形.
【知识网络】
【要点梳理】
要点一、轴对称
1.轴对称图形和轴对称
(1)轴对称图形 如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
(2)轴对称
定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.
要求诠释:成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;
②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.
(3)轴对称图形与轴对称的区别和联系
要点诠释: 轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的.联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.
2.线段的垂直平分线
线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
要点诠释:
线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件.
三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心.
3.角平分线
角平分线性质是:角平分线上的任意一点,到角两边的距离相等;反过来,在角的内部到角两边的距离相等的点在角平分线上.
要点诠释:
前者的前提条件是已经有角平分线了,即角被平分了;后者则是在结论中确定角被平分,一定要注意着两者的区别,在使用这两个定理时不要混淆了.
要点二、作轴对称图形
1.作轴对称图形
(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;
(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
要点三、等腰三角形
1.等腰三角形 (1)定义:有两边相等的三角形,叫做等腰三角形.
如图所示,在△ABC中,AB=AC,则它叫等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
要点诠释:等腰直角三角形的两个底角相等,且都等于45°.等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).
∠A=180°-2∠B,∠B=∠C= .
(2)等腰三角形性质
①等腰三角形的两个底角相等,即“等边对等角”;
②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.
(3)等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等 边”).
要点诠释:等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.
2.等边三角形
(1)定义:三条边都相等的三角形,叫做等边三角形.
要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包
括等边三角形.
(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.
(3)等边三角形的判定:
①三条边都相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角为 60°的等腰三角形是等边三角形.
【典型例题】
类型一、轴对称的性质与应用
1、(2019?阳谷县一模)若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是( )
A.OP1⊥OP2 B. OP1=OP2
C.OP1≠OP2 D. OP1⊥OP2且OP1=OP2
【思路点拨】根据轴对称的性质求出OP1、OP2的数量与夹角即可得解.
【答案】D;
【解析】解:如图,∵点P关于直线OA、OB的对称点P1、P2,
∴OP1=OP2=OP,
∠AOP=∠AOP1,∠BOP=∠BOP2,
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2,
=2(∠AOP+∠BOP),
=2∠AOB,
∵∠AOB=45°,
∴OP1⊥OP2成立.
故选D.
【总结升华】本题考查了轴对称的性质,是基础题,熟练掌握性质是解题的关键,利用图形更形象直观.
举一反三:
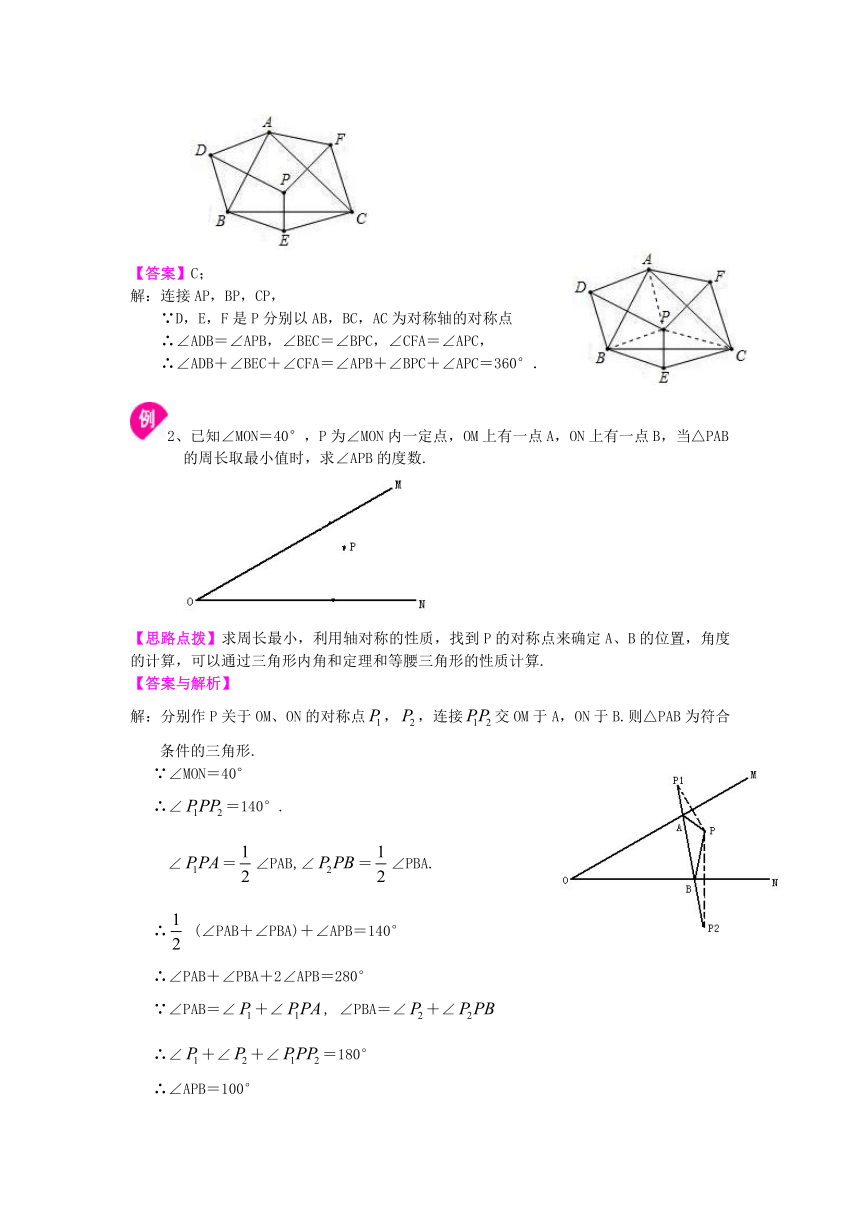
【变式】如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA=( )
A.180° B.270° C.360° D.480°
【答案】C;
解:连接AP,BP,CP,
∵D,E,F是P分别以AB,BC,AC为对称轴的对称点
∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
2、已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.
【思路点拨】求周长最小,利用轴对称的性质,找到P的对称点来确定A、B的位置,角度的计算,可以通过三角形内角和定理和等腰三角形的性质计算.
【答案与解析】
解:分别作P关于OM、ON的对称点,,连接交OM于A,ON于B.则△PAB为符合条件的三角形.
∵∠MON=40°
∴∠=140°.
∠=∠PAB,∠=∠PBA.
∴ (∠PAB+∠PBA)+∠APB=140°
∴∠PAB+∠PBA+2∠APB=280°
∵∠PAB=∠+∠, ∠PBA=∠+∠
∴∠+∠+∠=180°
∴∠APB=100°
【总结升华】将实际问题抽象或转化为几何模型,将周长的三条线段的和转化为一条线段,这样取得周长的最小值.
举一反三:
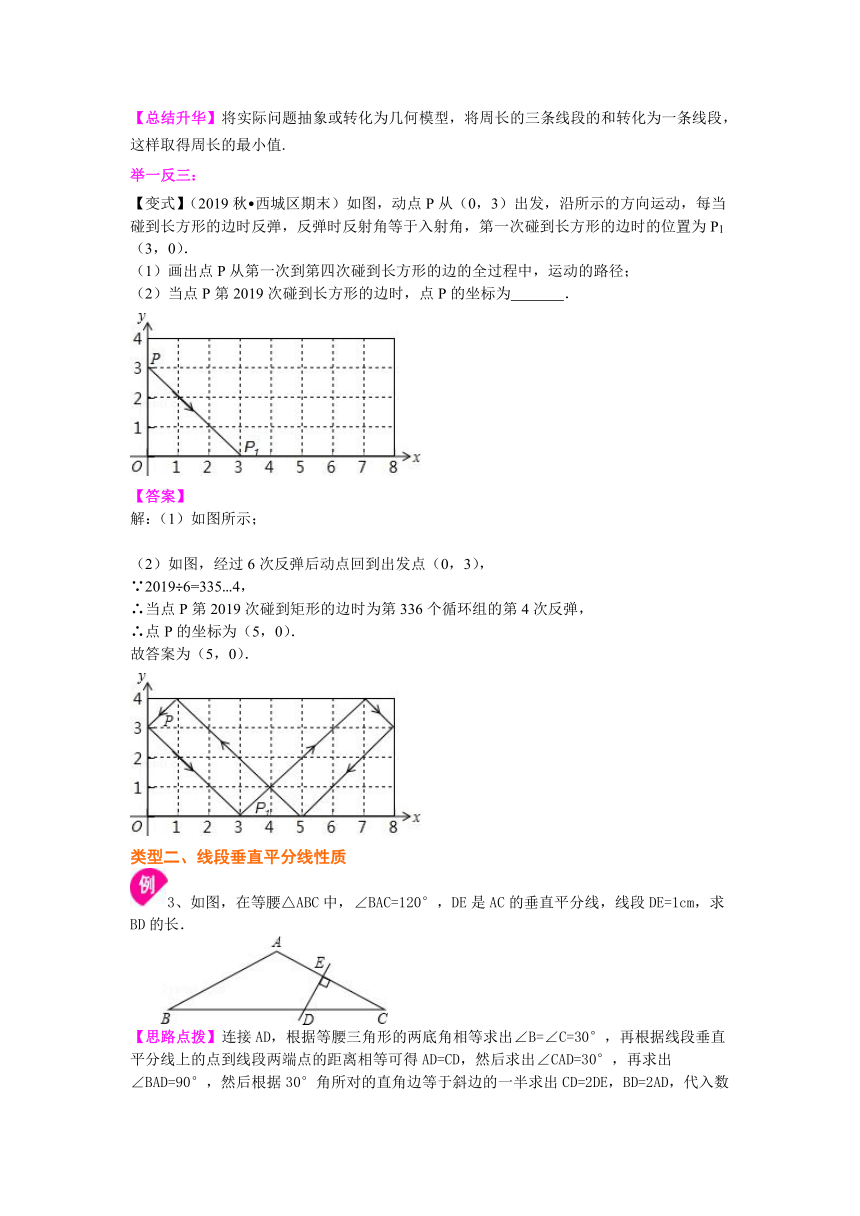
【变式】(2019秋?西城区期末)如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
(1)画出点P从第一次到第四次碰到长方形的边的全过程中,运动的路径;
(2)当点P第2019次碰到长方形的边时,点P的坐标为 .
【答案】
解:(1)如图所示;
(2)如图,经过6次反弹后动点回到出发点(0,3),
∵2019÷6=335…4,
∴当点P第2019次碰到矩形的边时为第336个循环组的第4次反弹,
∴点P的坐标为(5,0).
故答案为(5,0).
类型二、线段垂直平分线性质
3、如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,求BD的长.
【思路点拨】连接AD,根据等腰三角形的两底角相等求出∠B=∠C=30°,再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD,然后求出∠CAD=30°,再求出∠BAD=90°,然后根据30°角所对的直角边等于斜边的一半求出CD=2DE,BD=2AD,代入数据进行计算即可得解.
【答案与解析】
解:连接AD,∵等腰△ABC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠CAD=∠C=30°,
∴∠BAD=∠BAC﹣∠CAD=120°﹣30°=90°,
在Rt△CDE中,CD=2DE,
在Rt△ABD中,BD=2AD,
∴BD=4DE,
∵DE=1cm,
∴BD的长为4cm.
故答案为:4cm.
【总结升华】本题考查了等腰三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质是解题的关键.
举一反三
【变式】(2019春?芦溪县期中)如图,△ABC中,AB=AC,∠A=50°,DE是腰AB的垂直平分线,求∠DBC的度数.
【思路点拨】已知∠A=50°,AB=AC可得∠ABC=∠ACB,再由线段垂直平分线的性质可求出∠ABC=∠A,易求∠DBC.
【答案与解析】
解:∵∠A=50°,AB=AC,
∴∠ABC=∠ACB=(180°﹣∠A)=65°
又∵DE垂直且平分AB,
∴DB=AD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°.
即∠DBC的度数是15°.
【总结升华】本题考查的是等腰三角形的性质以及线段垂直平分线的性质.垂直平分线上任意一点,到线段两端点的距离相等.
类型三、角平分线性质
4、已知:如图,CD⊥AB于D,BE⊥AC于E,BE、CD相交于点O,且AO平分∠BAC,
求证:OB=OC.
证明:∵AO平分∠BAC,
∴OB=OC(角平分线上的点到角的两边距离相等)上述解答不正确,请你写出正确解答.
【思路点拨】由角平分线的性质可得OD=OE,然后证明△DOB≌△EOC,可得证OB=OC.
【答案与解析】
证明:∵AO平分∠BAC,CD⊥AB,BE⊥AC,
∴OD=OE,
在△DOB和△EOC中,
∠DOB=∠EOC,OD=OE,∠ODB=∠OEC,
∴△DOB≌△EOC(ASA),
∴OB=OC.
【总结升华】此题主要考查角平分线的性质和全等三角形的判定和性质,注意点到直线的距离是垂线段的长.
举一反三
【变式】如图,△ABC中,AB=AC,AD是角平分线,DE⊥AB,DF⊥AC,E、F为垂足,对于结论:①DE=DF;②BD=CD;③AD上任一点到AB、AC的距离相等;④AD上任一点到B、C的距离相等.其中正确的是( )
A.仅①② B.仅③④ C.仅①②③ D.①②③④
【答案】D;
类型四、等腰三角形的综合应用
5、如图①,△ABC中.AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC,CH⊥AB,垂足分别为E、F、H.易证PE+PF=CH.证明过程如下:
如图①,连接AP.
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴=AB?PE,=AC?PF,=AB?CH.
又∵,
∴AB?PE+AC?PF=AB?CH.∵AB=AC,∴PE+PF=CH.
(1)如图②,P为BC延长线上的点时,其它条件不变,PE、PF、CH又有怎样的数量关系?请写出你的猜想,并加以证明:
(2)填空:若∠A=30°,△ABC的面积为49,点P在直线BC上,且P到直线AC的距离为PF,当PF=3时,则AB边上的高CH=______.点P到AB边的距离PE=________.
【答案】7;4或10;
【解析】
解:(1)如图②,PE=PF+CH.证明如下:
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴=AB?PE,=AC?PF,=AB?CH,
∵=+,
∴AB?PE=AC?PF+AB?CH,
又∵AB=AC,
∴PE=PF+CH;
(2)∵在△ACH中,∠A=30°,
∴AC=2CH.
∵=AB?CH,AB=AC,
∴×2CH?CH=49,
∴CH=7.
分两种情况:
①P为底边BC上一点,如图①.
∵PE+PF=CH,
∴PE=CH-PF=7-3=4;
②P为BC延长线上的点时,如图②.
∵PE=PF+CH,
∴PE=3+7=10.
故答案为7;4或10.
【总结升华】本题考查了等腰三角形的性质与三角形的面积,难度适中,运用面积证明可使问题简便,(2)中分情况讨论是解题的关键.
6、已知,如图,∠1=12°,∠2=36°,∠3=48°,∠4=24°. 求的度数.
【答案与解析】
解:将沿AB翻折,得到,连结CE,
则,
∴∠1=∠5=12°.
∴60°
∵48°∴.
又∵∠2=36°,72°,
∴
∴BE=BC
∴为等边三角形.
∴
又垂直平分BC.
∴AE平分.
∴30°
∴∠ADB=30°
【总结升华】直接求很难,那就想想能不能通过翻折或旋转构造一个与全等的三角形,从而使其换个位置,看看会不会容易求.
举一反三:
【变式】在△ABC中,AB=AC,∠BAC=80°,D为形内一点,且∠DAB=∠DBA=10°,
求∠ACD的度数.
【答案】
解:作D关于BC中垂线的对称点E,连结AE,EC,DE
∴△ABD≌△ACE
∴AD=AE, ∠DAB=∠EAC=10°
∵∠BAC=80°,
∴∠DAE=60°,△ADE为等边三角形
∴∠AED=60°
∵∠DAB=∠DBA=10°
∴AD=BD=DE=EC
∴∠AEC=160°,
∴∠DEC=140°
∴∠DCE=20°
∴∠ACD=30°
类型五、等边三角形的综合应用
7、如图所示,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形.
(1)如图(1)所示,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?
(2)如图(2)所示,当点M在BC上时,其他条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图(2)证明;若不成立,请说明理由.
【答案与解析】
解:(1)EN=MF,点F在直线NE上.
证明:连接DF,DE,
∵ △ABC是等边三角形,
∴ AB=AC=BC.
又∵ D,E,F是△ABC三边的中点,
∴ DE,DF,EF为三角形的中位线.
∴ DE=DF=EF,∠FDE=60°.
又∠MDN+∠NDF=∠MDF,∠NDF+∠FDE=∠NDE,
∵△DMN为等边三角形,DM=DN,∠MDN=60°
∴ ∠MDF=∠NDE.
在△DMF和△DNE中,,
∴ △DMF≌△DNE,
∴ MF=NE,∠DMF=∠DNE.
∵∠DMF+60°=∠DNE+∠MFN
∴∠MFN=60°
∴FN∥AB,
又∵EF∥AB,
∴E、F、N在同一直线上.
(2)成立.证明:连结DE,DF,EF,
∵ △ABC是等边三角形,
∴ AB=AC=BC.
又∵ D,E,F是△ABC三边的中点,
∴ DE,DF,EF为三角形的中位线.
∴ DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,
∴ ∠MDF=∠NDE.
在△DMF和△DNE中,,
∴ △DMF≌△DNE,
∴ MF=NE.
【总结升华】此题综合应用了等边三角形的性质和判定,全等三角形的性质和判定.全等是证明线段相等的重要方法.(2)题的证明可以沿用(1)题的思路.
【巩固练习】
一.选择题
1. (2019?凤山县校级模拟)下列图形中对称轴只有两条的是( )
A. 圆 B. 等边三角形
C. 矩形 D. 等腰梯形
2. (2019?南充)如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A.30° B.45° C.60° D.75°
3.在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形;
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形;
C.等腰三角形是关于底边中线成轴对称的图形;
D.一条线段是关于经过该线段中点的直线成轴对称的图形 .
4. 小明从镜中看到电子钟示数是,则此时时间是( )
A.12:01 B.10:51 C.11:59 D.10:21
5. 如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=60° 那么∠EAC=( )
A.40° B.30° C.15° D.45°
6.如图,已知△ABC中,AC+BC=24,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
A
N
O
B M C
(22题图)
7. 如图,将△沿、、翻折,三个顶点均落在点处.若,则 的度数为( )
A. 49° B. 50° C. 51° D. 52°
8. 如图, △ABC中, ∠ACB=90°, ∠ABC=60°, AB的中垂线交BC的延长线于D,交AC于E, 已知DE=2.AC的长为( )
A.2 B.3 C. 4 D.5
二.填空题
9. (2019秋?上蔡县校级期末)如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪开,则下图展开得到的图形的面积为 .
10. 如图,在△ABC中,∠C=90度,AD平分∠BAC交BC于D,若BC=8,BD=5,则点D到AB的距离为 .
11.(2019?淮安一模)已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
12. 如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,PD的长为________.
13.如图所示,在△ABC中,AB=AC,点O在△ABC内,且∠OBC=∠OCA,∠BOC=110°,求∠A的度数为________.
14. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 .
15. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60o,若BE=6,DE=2,则BC=______________.
16. 如图,六边形ABCDEF的六个内角都相等.若AB=1,BC=CD=3,DE=2,则这个六边形的周长等于_________。
三.解答题
17.(2019?义乌市)在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(﹣1,1),(0,0)和(1,0).
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
18. 如图所示,AD是△ABC的角平分线,EF是AD的垂直平分线,交BC的延长线于点F,连接AF.求证:∠BAF=∠ACF.
19.已知:如图,在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD延长线上一点,且AE=AB.
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=DA,求证:ME=DC.
20.已知,∠BAC=90o,AB=AC,D为AC边上的中点,AN⊥BD于M,交BC于N.
求证:∠ADB=∠CDN
【答案与解析】
一.选择题
1. 【答案】C.
2. 【答案】C;
【解析】由题意,∠1=∠2,AN=MN,∠MGA=90°,得出NG=AM,AN=NG,推出
∠2=∠4,根据平行线的性质,得∠4=∠3,故∠1=∠2=∠3=×90°=30°,所以
∠DAG=60°故选C.
3.【答案】B;
【解析】全等的三角形不一定是成轴对称,而成轴对称的两个三角形一定是全等的.C 选项应为轴对称图形而不是成轴对称的图形.
4.【答案】B;
5.【答案】D;
【解析】先根据角平分线的定义求出∠DAC、∠DAB的度数;再根据角平分线的定义求出∠EAD的度数;再根据角的和差关系求解即可.
6. 【答案】B;
【解析】易证AN=ON,BM=OM,△CMN的周长等于AC+BC=24.
7. 【答案】C;
【解析】∠A=∠DOE,∠B=∠HOG,∠C=∠EOF,所以∠2=360°-180°-129°=51°.
8. 【答案】B;
【解析】连接AD,易证三角形ABD为等边三角形,CE=DE=1,AE=DE=2,所以AC=AE+CE=2+1=3.
二.填空题
9. 【答案】.
【解析】∵面积为1的正方形折叠以后展开面积不变,∴若把最后折叠成的三角形展开后面积仍为1,∵沿中位线减去小三角形的面积是△ABC的面积的,是×=,而剪去这样的三角形4个,则剪去的图形的面积是×4=.∴剩下部分展开所得图形的面积是1﹣=.
10.【答案】3;
【解析】根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离=CD=3.
11.【答案】14cm;
【解析】因为DE∥BC,得∠DOB=∠OBC,又BO是∠ABC的角平分线,则∠DBO=∠OBC,
所以∠DBO=∠DOB,得出BD=OD,同理:OE=EC,所以△ADE的周长
=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14cm.故答案是14cm.
12.【答案】2;
【解析】过P作PE⊥OB于E,所以PD=PE,因为PC∥OA,所以∠BCP=∠BOA=30°,
在Rt△PCE中,PE=PC,所以PE=×4=2,因为PE=PD,所以PD=2.
13.【答案】40°;
【解析】∵AB=AC,所以∠ABC=∠ACB, 又∵∠OBC=∠OCA,
∴∠ABC+∠ACB=2(∠OBC+∠OCB), ∵∠BOC=110°,
∴∠OBC+∠OCB=70°, ∴∠ABC+∠ACB=140°,
∴∠A=180°-(∠ABC+∠ACB)=40°.
14.【答案】4;
【解析】过D作DP⊥BC,此时DP长的最小值是.因为∠ABD=∠CBD,所以AD=DP=4.
15.【答案】8;
【解析】延长ED到BC于M,延长AD到BC与N,∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN,∵∠EBC=∠E=60°,∴△BEM为等边三角形,∵BE=6,DE=2,∴DM=4,∵∠NDM=30°,∴NM=2,∴BN=4,∴BC=8.
16.【答案】15;
【解析】因为六边形ABCDEF的六个内角都相等为120°,每个外角都为60°,向外作三个三角形,进而得到四个等边三角形,如图,设AF=,EF=,则有+1+3=++2=3+3+2=8所以=4,=2,六边形ABCDEF的周长=1+3+3+2+2+4=15.
三.解答题
17.【解析】
解:(1)如图2所示,C点的位置为(﹣1,2),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴;
(2)如图1所示:P(0,﹣1),P′(﹣1,﹣1)都符合题意.
18.【解析】
证明:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠ADF,
∵∠FAD=∠FAC+∠CAD,∠ADF=∠B+∠DAB,
∵AD是∠BAC的平分线,
∴∠DAB=∠CAD,
∴∠CAF=∠B,
∴∠BAC+∠FAC=∠B+∠BAC,
即∠BAF=∠ACF.
19.【解析】
解:(1)如图.
∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB==75°.
∵DB=DC,∠DCB=30°,
∴∠DBC=∠DCB=30°.
∴∠1=∠ABC-∠DBC=75°-30°=45°.
∵AB=AC,DB=DC,
∴AD所在直线垂直平分BC.
∴AD平分∠BAC.
∴∠2=∠BAC==15°.
∴∠ADE=∠1+∠2 =45°+15°=60°.
证明:(2)连接AM,取BE的中点N,连接AN.
∵△ADM中,DM=DA,∠ADE=60°,
∴△ADM为等边三角形.
∵△ABE中,AB=AE,N为BE的中点,
∴BN=NE,且AN⊥BE.
∴DN=NM.
∴BN-DN =NE-NM,
即 BD=ME.
∵DB=DC,
∴ME=DC.
20.【解析】
证明:作∠BAC的角平分线交BD于H
∴∠BAH=∠CAH=45o
∵AB=AC,
∴∠ABC=∠C=45 o
∴∠BAH=∠C
∵AN⊥BD于M,
∴∠AMD=90o
∴∠NAD+∠ADB=90o
∵∠BAC=90o
∴∠ABD+∠ADB=90o
∴∠ABD=∠NAC
在△ABH与△CAN中
∴△ABH≌△CAN
∴AH=CN
∵D为AC边上的中点
∴AD=CD
在△AHD与△CND中
∴△AHD≌△CND
∴∠ADB=∠CDN.
【学习目标】
1.认识和欣赏身边的轴对称图形,增进学习数学的兴趣.
2.了解轴对称的概念,探索轴对称、轴对称图形的基本性质及它们的简单应用.
3.探索线段的垂直平分线、角平分线和等腰三角形的性质以及判定方法.
4.能按照要求,画出一些轴对称图形.
【知识网络】
【要点梳理】
要点一、轴对称
1.轴对称图形和轴对称
(1)轴对称图形 如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
(2)轴对称
定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.
要求诠释:成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;
②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.
(3)轴对称图形与轴对称的区别和联系
要点诠释: 轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的.联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.
2.线段的垂直平分线
线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
要点诠释:
线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件.
三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心.
3.角平分线
角平分线性质是:角平分线上的任意一点,到角两边的距离相等;反过来,在角的内部到角两边的距离相等的点在角平分线上.
要点诠释:
前者的前提条件是已经有角平分线了,即角被平分了;后者则是在结论中确定角被平分,一定要注意着两者的区别,在使用这两个定理时不要混淆了.
要点二、作轴对称图形
1.作轴对称图形
(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;
(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
要点三、等腰三角形
1.等腰三角形 (1)定义:有两边相等的三角形,叫做等腰三角形.
如图所示,在△ABC中,AB=AC,则它叫等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
要点诠释:等腰直角三角形的两个底角相等,且都等于45°.等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).
∠A=180°-2∠B,∠B=∠C= .
(2)等腰三角形性质
①等腰三角形的两个底角相等,即“等边对等角”;
②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.
(3)等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等 边”).
要点诠释:等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.
2.等边三角形
(1)定义:三条边都相等的三角形,叫做等边三角形.
要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包
括等边三角形.
(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.
(3)等边三角形的判定:
①三条边都相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角为 60°的等腰三角形是等边三角形.
【典型例题】
类型一、轴对称的性质与应用
1、(2019?阳谷县一模)若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是( )
A.OP1⊥OP2 B. OP1=OP2
C.OP1≠OP2 D. OP1⊥OP2且OP1=OP2
【思路点拨】根据轴对称的性质求出OP1、OP2的数量与夹角即可得解.
【答案】D;
【解析】解:如图,∵点P关于直线OA、OB的对称点P1、P2,
∴OP1=OP2=OP,
∠AOP=∠AOP1,∠BOP=∠BOP2,
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2,
=2(∠AOP+∠BOP),
=2∠AOB,
∵∠AOB=45°,
∴OP1⊥OP2成立.
故选D.
【总结升华】本题考查了轴对称的性质,是基础题,熟练掌握性质是解题的关键,利用图形更形象直观.
举一反三:
【变式】如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA=( )
A.180° B.270° C.360° D.480°
【答案】C;
解:连接AP,BP,CP,
∵D,E,F是P分别以AB,BC,AC为对称轴的对称点
∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
2、已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.
【思路点拨】求周长最小,利用轴对称的性质,找到P的对称点来确定A、B的位置,角度的计算,可以通过三角形内角和定理和等腰三角形的性质计算.
【答案与解析】
解:分别作P关于OM、ON的对称点,,连接交OM于A,ON于B.则△PAB为符合条件的三角形.
∵∠MON=40°
∴∠=140°.
∠=∠PAB,∠=∠PBA.
∴ (∠PAB+∠PBA)+∠APB=140°
∴∠PAB+∠PBA+2∠APB=280°
∵∠PAB=∠+∠, ∠PBA=∠+∠
∴∠+∠+∠=180°
∴∠APB=100°
【总结升华】将实际问题抽象或转化为几何模型,将周长的三条线段的和转化为一条线段,这样取得周长的最小值.
举一反三:
【变式】(2019秋?西城区期末)如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
(1)画出点P从第一次到第四次碰到长方形的边的全过程中,运动的路径;
(2)当点P第2019次碰到长方形的边时,点P的坐标为 .
【答案】
解:(1)如图所示;
(2)如图,经过6次反弹后动点回到出发点(0,3),
∵2019÷6=335…4,
∴当点P第2019次碰到矩形的边时为第336个循环组的第4次反弹,
∴点P的坐标为(5,0).
故答案为(5,0).
类型二、线段垂直平分线性质
3、如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,求BD的长.
【思路点拨】连接AD,根据等腰三角形的两底角相等求出∠B=∠C=30°,再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD,然后求出∠CAD=30°,再求出∠BAD=90°,然后根据30°角所对的直角边等于斜边的一半求出CD=2DE,BD=2AD,代入数据进行计算即可得解.
【答案与解析】
解:连接AD,∵等腰△ABC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠CAD=∠C=30°,
∴∠BAD=∠BAC﹣∠CAD=120°﹣30°=90°,
在Rt△CDE中,CD=2DE,
在Rt△ABD中,BD=2AD,
∴BD=4DE,
∵DE=1cm,
∴BD的长为4cm.
故答案为:4cm.
【总结升华】本题考查了等腰三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质是解题的关键.
举一反三
【变式】(2019春?芦溪县期中)如图,△ABC中,AB=AC,∠A=50°,DE是腰AB的垂直平分线,求∠DBC的度数.
【思路点拨】已知∠A=50°,AB=AC可得∠ABC=∠ACB,再由线段垂直平分线的性质可求出∠ABC=∠A,易求∠DBC.
【答案与解析】
解:∵∠A=50°,AB=AC,
∴∠ABC=∠ACB=(180°﹣∠A)=65°
又∵DE垂直且平分AB,
∴DB=AD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°.
即∠DBC的度数是15°.
【总结升华】本题考查的是等腰三角形的性质以及线段垂直平分线的性质.垂直平分线上任意一点,到线段两端点的距离相等.
类型三、角平分线性质
4、已知:如图,CD⊥AB于D,BE⊥AC于E,BE、CD相交于点O,且AO平分∠BAC,
求证:OB=OC.
证明:∵AO平分∠BAC,
∴OB=OC(角平分线上的点到角的两边距离相等)上述解答不正确,请你写出正确解答.
【思路点拨】由角平分线的性质可得OD=OE,然后证明△DOB≌△EOC,可得证OB=OC.
【答案与解析】
证明:∵AO平分∠BAC,CD⊥AB,BE⊥AC,
∴OD=OE,
在△DOB和△EOC中,
∠DOB=∠EOC,OD=OE,∠ODB=∠OEC,
∴△DOB≌△EOC(ASA),
∴OB=OC.
【总结升华】此题主要考查角平分线的性质和全等三角形的判定和性质,注意点到直线的距离是垂线段的长.
举一反三
【变式】如图,△ABC中,AB=AC,AD是角平分线,DE⊥AB,DF⊥AC,E、F为垂足,对于结论:①DE=DF;②BD=CD;③AD上任一点到AB、AC的距离相等;④AD上任一点到B、C的距离相等.其中正确的是( )
A.仅①② B.仅③④ C.仅①②③ D.①②③④
【答案】D;
类型四、等腰三角形的综合应用
5、如图①,△ABC中.AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC,CH⊥AB,垂足分别为E、F、H.易证PE+PF=CH.证明过程如下:
如图①,连接AP.
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴=AB?PE,=AC?PF,=AB?CH.
又∵,
∴AB?PE+AC?PF=AB?CH.∵AB=AC,∴PE+PF=CH.
(1)如图②,P为BC延长线上的点时,其它条件不变,PE、PF、CH又有怎样的数量关系?请写出你的猜想,并加以证明:
(2)填空:若∠A=30°,△ABC的面积为49,点P在直线BC上,且P到直线AC的距离为PF,当PF=3时,则AB边上的高CH=______.点P到AB边的距离PE=________.
【答案】7;4或10;
【解析】
解:(1)如图②,PE=PF+CH.证明如下:
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴=AB?PE,=AC?PF,=AB?CH,
∵=+,
∴AB?PE=AC?PF+AB?CH,
又∵AB=AC,
∴PE=PF+CH;
(2)∵在△ACH中,∠A=30°,
∴AC=2CH.
∵=AB?CH,AB=AC,
∴×2CH?CH=49,
∴CH=7.
分两种情况:
①P为底边BC上一点,如图①.
∵PE+PF=CH,
∴PE=CH-PF=7-3=4;
②P为BC延长线上的点时,如图②.
∵PE=PF+CH,
∴PE=3+7=10.
故答案为7;4或10.
【总结升华】本题考查了等腰三角形的性质与三角形的面积,难度适中,运用面积证明可使问题简便,(2)中分情况讨论是解题的关键.
6、已知,如图,∠1=12°,∠2=36°,∠3=48°,∠4=24°. 求的度数.
【答案与解析】
解:将沿AB翻折,得到,连结CE,
则,
∴∠1=∠5=12°.
∴60°
∵48°∴.
又∵∠2=36°,72°,
∴
∴BE=BC
∴为等边三角形.
∴
又垂直平分BC.
∴AE平分.
∴30°
∴∠ADB=30°
【总结升华】直接求很难,那就想想能不能通过翻折或旋转构造一个与全等的三角形,从而使其换个位置,看看会不会容易求.
举一反三:
【变式】在△ABC中,AB=AC,∠BAC=80°,D为形内一点,且∠DAB=∠DBA=10°,
求∠ACD的度数.
【答案】
解:作D关于BC中垂线的对称点E,连结AE,EC,DE
∴△ABD≌△ACE
∴AD=AE, ∠DAB=∠EAC=10°
∵∠BAC=80°,
∴∠DAE=60°,△ADE为等边三角形
∴∠AED=60°
∵∠DAB=∠DBA=10°
∴AD=BD=DE=EC
∴∠AEC=160°,
∴∠DEC=140°
∴∠DCE=20°
∴∠ACD=30°
类型五、等边三角形的综合应用
7、如图所示,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形.
(1)如图(1)所示,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?
(2)如图(2)所示,当点M在BC上时,其他条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图(2)证明;若不成立,请说明理由.
【答案与解析】
解:(1)EN=MF,点F在直线NE上.
证明:连接DF,DE,
∵ △ABC是等边三角形,
∴ AB=AC=BC.
又∵ D,E,F是△ABC三边的中点,
∴ DE,DF,EF为三角形的中位线.
∴ DE=DF=EF,∠FDE=60°.
又∠MDN+∠NDF=∠MDF,∠NDF+∠FDE=∠NDE,
∵△DMN为等边三角形,DM=DN,∠MDN=60°
∴ ∠MDF=∠NDE.
在△DMF和△DNE中,,
∴ △DMF≌△DNE,
∴ MF=NE,∠DMF=∠DNE.
∵∠DMF+60°=∠DNE+∠MFN
∴∠MFN=60°
∴FN∥AB,
又∵EF∥AB,
∴E、F、N在同一直线上.
(2)成立.证明:连结DE,DF,EF,
∵ △ABC是等边三角形,
∴ AB=AC=BC.
又∵ D,E,F是△ABC三边的中点,
∴ DE,DF,EF为三角形的中位线.
∴ DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,
∴ ∠MDF=∠NDE.
在△DMF和△DNE中,,
∴ △DMF≌△DNE,
∴ MF=NE.
【总结升华】此题综合应用了等边三角形的性质和判定,全等三角形的性质和判定.全等是证明线段相等的重要方法.(2)题的证明可以沿用(1)题的思路.
【巩固练习】
一.选择题
1. (2019?凤山县校级模拟)下列图形中对称轴只有两条的是( )
A. 圆 B. 等边三角形
C. 矩形 D. 等腰梯形
2. (2019?南充)如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A.30° B.45° C.60° D.75°
3.在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形;
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形;
C.等腰三角形是关于底边中线成轴对称的图形;
D.一条线段是关于经过该线段中点的直线成轴对称的图形 .
4. 小明从镜中看到电子钟示数是,则此时时间是( )
A.12:01 B.10:51 C.11:59 D.10:21
5. 如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=60° 那么∠EAC=( )
A.40° B.30° C.15° D.45°
6.如图,已知△ABC中,AC+BC=24,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
A
N
O
B M C
(22题图)
7. 如图,将△沿、、翻折,三个顶点均落在点处.若,则 的度数为( )
A. 49° B. 50° C. 51° D. 52°
8. 如图, △ABC中, ∠ACB=90°, ∠ABC=60°, AB的中垂线交BC的延长线于D,交AC于E, 已知DE=2.AC的长为( )
A.2 B.3 C. 4 D.5
二.填空题
9. (2019秋?上蔡县校级期末)如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪开,则下图展开得到的图形的面积为 .
10. 如图,在△ABC中,∠C=90度,AD平分∠BAC交BC于D,若BC=8,BD=5,则点D到AB的距离为 .
11.(2019?淮安一模)已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
12. 如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,PD的长为________.
13.如图所示,在△ABC中,AB=AC,点O在△ABC内,且∠OBC=∠OCA,∠BOC=110°,求∠A的度数为________.
14. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 .
15. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60o,若BE=6,DE=2,则BC=______________.
16. 如图,六边形ABCDEF的六个内角都相等.若AB=1,BC=CD=3,DE=2,则这个六边形的周长等于_________。
三.解答题
17.(2019?义乌市)在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(﹣1,1),(0,0)和(1,0).
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
18. 如图所示,AD是△ABC的角平分线,EF是AD的垂直平分线,交BC的延长线于点F,连接AF.求证:∠BAF=∠ACF.
19.已知:如图,在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD延长线上一点,且AE=AB.
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=DA,求证:ME=DC.
20.已知,∠BAC=90o,AB=AC,D为AC边上的中点,AN⊥BD于M,交BC于N.
求证:∠ADB=∠CDN
【答案与解析】
一.选择题
1. 【答案】C.
2. 【答案】C;
【解析】由题意,∠1=∠2,AN=MN,∠MGA=90°,得出NG=AM,AN=NG,推出
∠2=∠4,根据平行线的性质,得∠4=∠3,故∠1=∠2=∠3=×90°=30°,所以
∠DAG=60°故选C.
3.【答案】B;
【解析】全等的三角形不一定是成轴对称,而成轴对称的两个三角形一定是全等的.C 选项应为轴对称图形而不是成轴对称的图形.
4.【答案】B;
5.【答案】D;
【解析】先根据角平分线的定义求出∠DAC、∠DAB的度数;再根据角平分线的定义求出∠EAD的度数;再根据角的和差关系求解即可.
6. 【答案】B;
【解析】易证AN=ON,BM=OM,△CMN的周长等于AC+BC=24.
7. 【答案】C;
【解析】∠A=∠DOE,∠B=∠HOG,∠C=∠EOF,所以∠2=360°-180°-129°=51°.
8. 【答案】B;
【解析】连接AD,易证三角形ABD为等边三角形,CE=DE=1,AE=DE=2,所以AC=AE+CE=2+1=3.
二.填空题
9. 【答案】.
【解析】∵面积为1的正方形折叠以后展开面积不变,∴若把最后折叠成的三角形展开后面积仍为1,∵沿中位线减去小三角形的面积是△ABC的面积的,是×=,而剪去这样的三角形4个,则剪去的图形的面积是×4=.∴剩下部分展开所得图形的面积是1﹣=.
10.【答案】3;
【解析】根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离=CD=3.
11.【答案】14cm;
【解析】因为DE∥BC,得∠DOB=∠OBC,又BO是∠ABC的角平分线,则∠DBO=∠OBC,
所以∠DBO=∠DOB,得出BD=OD,同理:OE=EC,所以△ADE的周长
=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14cm.故答案是14cm.
12.【答案】2;
【解析】过P作PE⊥OB于E,所以PD=PE,因为PC∥OA,所以∠BCP=∠BOA=30°,
在Rt△PCE中,PE=PC,所以PE=×4=2,因为PE=PD,所以PD=2.
13.【答案】40°;
【解析】∵AB=AC,所以∠ABC=∠ACB, 又∵∠OBC=∠OCA,
∴∠ABC+∠ACB=2(∠OBC+∠OCB), ∵∠BOC=110°,
∴∠OBC+∠OCB=70°, ∴∠ABC+∠ACB=140°,
∴∠A=180°-(∠ABC+∠ACB)=40°.
14.【答案】4;
【解析】过D作DP⊥BC,此时DP长的最小值是.因为∠ABD=∠CBD,所以AD=DP=4.
15.【答案】8;
【解析】延长ED到BC于M,延长AD到BC与N,∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN,∵∠EBC=∠E=60°,∴△BEM为等边三角形,∵BE=6,DE=2,∴DM=4,∵∠NDM=30°,∴NM=2,∴BN=4,∴BC=8.
16.【答案】15;
【解析】因为六边形ABCDEF的六个内角都相等为120°,每个外角都为60°,向外作三个三角形,进而得到四个等边三角形,如图,设AF=,EF=,则有+1+3=++2=3+3+2=8所以=4,=2,六边形ABCDEF的周长=1+3+3+2+2+4=15.
三.解答题
17.【解析】
解:(1)如图2所示,C点的位置为(﹣1,2),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴;
(2)如图1所示:P(0,﹣1),P′(﹣1,﹣1)都符合题意.
18.【解析】
证明:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠ADF,
∵∠FAD=∠FAC+∠CAD,∠ADF=∠B+∠DAB,
∵AD是∠BAC的平分线,
∴∠DAB=∠CAD,
∴∠CAF=∠B,
∴∠BAC+∠FAC=∠B+∠BAC,
即∠BAF=∠ACF.
19.【解析】
解:(1)如图.
∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB==75°.
∵DB=DC,∠DCB=30°,
∴∠DBC=∠DCB=30°.
∴∠1=∠ABC-∠DBC=75°-30°=45°.
∵AB=AC,DB=DC,
∴AD所在直线垂直平分BC.
∴AD平分∠BAC.
∴∠2=∠BAC==15°.
∴∠ADE=∠1+∠2 =45°+15°=60°.
证明:(2)连接AM,取BE的中点N,连接AN.
∵△ADM中,DM=DA,∠ADE=60°,
∴△ADM为等边三角形.
∵△ABE中,AB=AE,N为BE的中点,
∴BN=NE,且AN⊥BE.
∴DN=NM.
∴BN-DN =NE-NM,
即 BD=ME.
∵DB=DC,
∴ME=DC.
20.【解析】
证明:作∠BAC的角平分线交BD于H
∴∠BAH=∠CAH=45o
∵AB=AC,
∴∠ABC=∠C=45 o
∴∠BAH=∠C
∵AN⊥BD于M,
∴∠AMD=90o
∴∠NAD+∠ADB=90o
∵∠BAC=90o
∴∠ABD+∠ADB=90o
∴∠ABD=∠NAC
在△ABH与△CAN中
∴△ABH≌△CAN
∴AH=CN
∵D为AC边上的中点
∴AD=CD
在△AHD与△CND中
∴△AHD≌△CND
∴∠ADB=∠CDN.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
