(新教材)鲁教版物理课件必修二2.1.2(物理):40张PPT
文档属性
| 名称 | (新教材)鲁教版物理课件必修二2.1.2(物理):40张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-10-09 00:00:00 | ||
图片预览










文档简介
课件40张PPT。第2课时
小船渡河和关联速度问题一 小船渡河模型
1.模型特点:两个分运动和合运动都是匀速直线运动,其中一个分运动的速度大小、方向都不变,另一个分运动的速度大小不变,研究其速度方向不同时对合运动的影响。这样的运动系统可看作小船渡河模型。2.模型分析。
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。(3)两个极值。
a.过河时间最短:v1⊥v2,tmin= (d为河宽)。
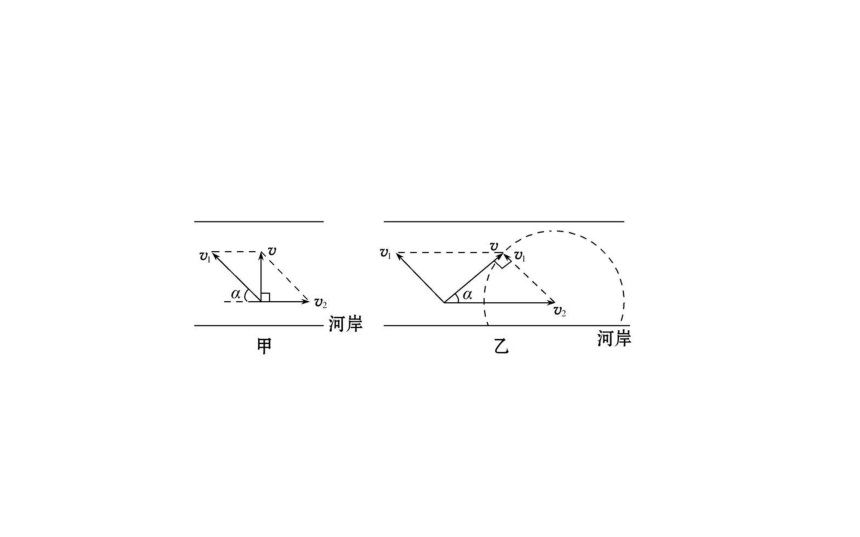
b.过河位移最小:v⊥v2(前提v1>v2),如图甲所示,此时
xmin=d,船头指向上游与河岸夹角为α,cosα= ;v1
⊥v(前提v1 。【思考·讨论】
在渡河小游戏中,一条匀速前进的小船要
过河,怎样使小船渡河时间最短?
(科学思维)
提示:船头垂直于河岸渡河时间最短。【典例示范】
一小船要渡河,河宽d=180 m,水流速度v1=2.5 m/s。若船在静水中的速度为v2=5 m/s,求:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?【解析】
(1)欲使船在最短时间内渡河,船头应朝垂
直河岸方向
当船头垂直河岸时,如图甲所示,合速度为
倾斜方向,垂直分速度为v2=5 m/s(2)欲使船渡河航程最短,应垂直河岸渡河,船头应朝上
游与垂直河岸方向成某一夹角α,如图乙所示;
有v2sin α=v1,得α=30°
所以当船头向上游偏30°时航程最短
x′=d =180 m答案:(1)朝垂直河岸方向 36 s 90 m
(2)朝上游与垂直河岸方向成30°角 24 s 180 m
【误区警示】分析小船渡河问题应注意的三个方面
(1)要使船垂直于河岸横渡,即路程最短,则v船在水流方向的分速度和水流速度等大、反向,这种情况只适用于v船>v水时。
(2)要使船渡河时间最短,船头应垂直指向河岸,即v船与水流方向垂直,这种情况对v船≥v水及v船1.如图所示,小船过河时,船头偏向上游与
水流方向成α角,船相对于静水的速度为v,
其航线恰好垂直于河岸。现水流速度稍有减小,为保持
航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大v B.减小α角,减小v
C.减小α角,保持v不变 D.增大α角,保持v不变【解析】选B。由题意可知,船相对水的速度为v,其航线恰好垂直于河岸,当水流速度稍有减小,为保持航线不变,且准时到达对岸,则如图所示,可知减小α角,减小v,故选项B正确,A、C、D错误。2.(多选)一艘船的船头始终正对河岸方向行驶,如图所示。已知:船在静水中行驶的速度为v1,水流速度为v2,河宽为d。则下列判断正确的是 ( )A.船渡河时间为
B.船渡河时间为
C.船渡河过程被冲到下游的距离为
D.船渡河过程被冲到下游的距离为【解析】选A、C。船渡河时间与分运动的时间相等,船
头垂直河岸方向行驶,故t= ,A正确、B错误;船渡河
过程被冲到下游的距离为s2=v2t= ,C正确、D错误。【补偿训练】
1.甲船以v甲的船速用最短的时间横渡过河,乙船以
v乙的船速从同一地点以最短的航程过河,两船轨迹恰好
重合(设河水速度保持不变),则两船过河所用的时间之
比为 ( )
A.v甲∶v乙 B.v乙∶v甲【解析】选C。要使甲船以最短时间过河,则甲船的船
头应是垂直河岸,要使乙船以最短的航程过河而又和
甲船的轨迹重合,v乙必和轨迹垂直,如图所示。
从已知条件和图中的几何关系可得到t甲= ,t乙= ,
而v水= ,v乙=v甲cosθ,联立可得到t甲∶t乙
= ,故C项正确。2.设有一条河,其宽度为700 m,河水均匀流动,流速为
2 m/s,汽船相对于河水的运动速度为4 m/s,则汽船的船头应偏向哪个方向行驶,才能恰好到达河的正对岸?渡河过程经历多长时间?【解析】如图所示,汽船实际的运动可以看作是汽船斜
向上游方向和沿水流方向两个分运动的合运动,由图可
知sinα= =0.5,α=30°
v= m/s≈3.5 m/s,
渡河时间为t= s=200 s=3.3 min。
答案:斜向上游30°行驶 3.3 min二 关联速度问题
1.常见问题:物体斜拉绳或绳斜拉物体,如图甲、乙所示。2.规律:由于绳不可伸长,绳两端所连物体的速度沿着绳方向的分速度大小相等。3.速度的分解方法:图甲中小车向右运动拉绳的结果,一方面是滑轮右侧绳变长,另一方面是使绳绕滑轮转动,由此可确定车的速度分解为沿绳和垂直绳的两个分速度,甲、乙两图的速度分解如图丙、丁所示。
4.进行速度分解:
(1)要分清合速度与分速度:合速度就是物体的实际运动的速度。
(2)分析物体的实际运动是由哪两个分运动合成的,找出相应的分速度。
(3)解决问题的关键:不可伸长的绳和杆,虽各点速度不同,但沿绳或杆轴线上的速度大小是相同的。【典例示范】
如图所示,人用绳子通过定滑轮以不变的速度v0拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。 【解析】物体A的运动(即绳的末端的运
动)可看作两个分运动的合成:一是沿绳
的方向被牵引,绳长缩短。绳长缩短的
速度即v1=v0;二是随着绳以定滑轮为圆心的摆动,它不
改变绳长,只改变角θ的值。这样就可以将vA按图示方
向进行分解。所以v1及v2实际上就是vA的两个分速度,
如图所示,由此可得vA= 。答案: 【规律方法】处理关联速度问题的分析思路
(1)选取合适的连接点(该点必须能明显地体现某个分运动)。
(2)确定该点合速度方向(通常以物体的实际速度为合速度)且合速度方向始终不变。
(3)确定该点合速度(实际速度)的实际运动效果,从而依据平行四边形定则确定分速度方向。(4)作出速度分解的示意图,寻找速度关系。【母题追问】
1.请根据运动的合成与分解的性质,判断【典例示范】情境中,物体A做什么运动 ( )
A.匀速直线运动 B.匀加速直线运动
C.匀减速直线运动 D.变加速直线运动【解析】选D。物体A的速度为vA= 。由于人匀速
运动,船越往左,θ越大,cosθ越小,vA越大,所以船加
速运动,但并非匀加速直线运动,所以选D。2.请根据运动的合成与分解的性质以及牛顿第二定律,判断【典例示范】情境中,物体A所受的合力 ( )
A.物体A所受的合力为零 B.物体A所受合力向左
C.物体A所受合力向右 D.物体A所受合力不变【解析】选B。物体A的速度为vA= 。
由于人匀速运动,船越往左,θ越大,cosθ越小,vA越大,
所以船加速运动,但并非匀加速直线运动,所以物体A所
受合力向左,是变化的,故选B。【补偿训练】
如图所示,用一小车通过轻绳提升
一货物,某一时刻,两段绳恰好垂直,且
拴在小车一端的绳与水平方向的夹角
为θ,此时小车的速度为v0,则此时货物的速度为( )
A. B.v0sinθ C.v0cosθ D.v0【解析】选D。如图所示,车的速度等于沿绳子方向和垂直于绳子方向速度的合速度,根据平行四边形定则,有v0cosθ=v绳,而货物的速度等于沿绳子方向和垂直于绳子方向速度的合速度。则有v货cos α=v绳。由于两绳子相互垂直,所以α=θ,则由以上两式可得,货物的速度就等于小车的速度。故选D。【拓展例题】考查内容:运动分解的实际应用
【典例】如图,人沿平直的河岸以速度v
行走,且通过不可伸长的绳拖船,船沿绳
的方向行进,此过程中绳始终与水面平行。
当绳与河岸的夹角为α时,船的速率为 ( )
A.vsinα B. C.vcosα D. 【解析】选C。把人的速度v沿着绳子方向和垂直于绳
子方向分解,如图所示。
其中v1=vcosα,所以船的速度等于vcosα。因此C选项
正确。
小船渡河和关联速度问题一 小船渡河模型
1.模型特点:两个分运动和合运动都是匀速直线运动,其中一个分运动的速度大小、方向都不变,另一个分运动的速度大小不变,研究其速度方向不同时对合运动的影响。这样的运动系统可看作小船渡河模型。2.模型分析。
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。(3)两个极值。
a.过河时间最短:v1⊥v2,tmin= (d为河宽)。
b.过河位移最小:v⊥v2(前提v1>v2),如图甲所示,此时
xmin=d,船头指向上游与河岸夹角为α,cosα= ;v1
⊥v(前提v1
在渡河小游戏中,一条匀速前进的小船要
过河,怎样使小船渡河时间最短?
(科学思维)
提示:船头垂直于河岸渡河时间最短。【典例示范】
一小船要渡河,河宽d=180 m,水流速度v1=2.5 m/s。若船在静水中的速度为v2=5 m/s,求:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?【解析】
(1)欲使船在最短时间内渡河,船头应朝垂
直河岸方向
当船头垂直河岸时,如图甲所示,合速度为
倾斜方向,垂直分速度为v2=5 m/s(2)欲使船渡河航程最短,应垂直河岸渡河,船头应朝上
游与垂直河岸方向成某一夹角α,如图乙所示;
有v2sin α=v1,得α=30°
所以当船头向上游偏30°时航程最短
x′=d =180 m答案:(1)朝垂直河岸方向 36 s 90 m
(2)朝上游与垂直河岸方向成30°角 24 s 180 m
【误区警示】分析小船渡河问题应注意的三个方面
(1)要使船垂直于河岸横渡,即路程最短,则v船在水流方向的分速度和水流速度等大、反向,这种情况只适用于v船>v水时。
(2)要使船渡河时间最短,船头应垂直指向河岸,即v船与水流方向垂直,这种情况对v船≥v水及v船
水流方向成α角,船相对于静水的速度为v,
其航线恰好垂直于河岸。现水流速度稍有减小,为保持
航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大v B.减小α角,减小v
C.减小α角,保持v不变 D.增大α角,保持v不变【解析】选B。由题意可知,船相对水的速度为v,其航线恰好垂直于河岸,当水流速度稍有减小,为保持航线不变,且准时到达对岸,则如图所示,可知减小α角,减小v,故选项B正确,A、C、D错误。2.(多选)一艘船的船头始终正对河岸方向行驶,如图所示。已知:船在静水中行驶的速度为v1,水流速度为v2,河宽为d。则下列判断正确的是 ( )A.船渡河时间为
B.船渡河时间为
C.船渡河过程被冲到下游的距离为
D.船渡河过程被冲到下游的距离为【解析】选A、C。船渡河时间与分运动的时间相等,船
头垂直河岸方向行驶,故t= ,A正确、B错误;船渡河
过程被冲到下游的距离为s2=v2t= ,C正确、D错误。【补偿训练】
1.甲船以v甲的船速用最短的时间横渡过河,乙船以
v乙的船速从同一地点以最短的航程过河,两船轨迹恰好
重合(设河水速度保持不变),则两船过河所用的时间之
比为 ( )
A.v甲∶v乙 B.v乙∶v甲【解析】选C。要使甲船以最短时间过河,则甲船的船
头应是垂直河岸,要使乙船以最短的航程过河而又和
甲船的轨迹重合,v乙必和轨迹垂直,如图所示。
从已知条件和图中的几何关系可得到t甲= ,t乙= ,
而v水= ,v乙=v甲cosθ,联立可得到t甲∶t乙
= ,故C项正确。2.设有一条河,其宽度为700 m,河水均匀流动,流速为
2 m/s,汽船相对于河水的运动速度为4 m/s,则汽船的船头应偏向哪个方向行驶,才能恰好到达河的正对岸?渡河过程经历多长时间?【解析】如图所示,汽船实际的运动可以看作是汽船斜
向上游方向和沿水流方向两个分运动的合运动,由图可
知sinα= =0.5,α=30°
v= m/s≈3.5 m/s,
渡河时间为t= s=200 s=3.3 min。
答案:斜向上游30°行驶 3.3 min二 关联速度问题
1.常见问题:物体斜拉绳或绳斜拉物体,如图甲、乙所示。2.规律:由于绳不可伸长,绳两端所连物体的速度沿着绳方向的分速度大小相等。3.速度的分解方法:图甲中小车向右运动拉绳的结果,一方面是滑轮右侧绳变长,另一方面是使绳绕滑轮转动,由此可确定车的速度分解为沿绳和垂直绳的两个分速度,甲、乙两图的速度分解如图丙、丁所示。
4.进行速度分解:
(1)要分清合速度与分速度:合速度就是物体的实际运动的速度。
(2)分析物体的实际运动是由哪两个分运动合成的,找出相应的分速度。
(3)解决问题的关键:不可伸长的绳和杆,虽各点速度不同,但沿绳或杆轴线上的速度大小是相同的。【典例示范】
如图所示,人用绳子通过定滑轮以不变的速度v0拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。 【解析】物体A的运动(即绳的末端的运
动)可看作两个分运动的合成:一是沿绳
的方向被牵引,绳长缩短。绳长缩短的
速度即v1=v0;二是随着绳以定滑轮为圆心的摆动,它不
改变绳长,只改变角θ的值。这样就可以将vA按图示方
向进行分解。所以v1及v2实际上就是vA的两个分速度,
如图所示,由此可得vA= 。答案: 【规律方法】处理关联速度问题的分析思路
(1)选取合适的连接点(该点必须能明显地体现某个分运动)。
(2)确定该点合速度方向(通常以物体的实际速度为合速度)且合速度方向始终不变。
(3)确定该点合速度(实际速度)的实际运动效果,从而依据平行四边形定则确定分速度方向。(4)作出速度分解的示意图,寻找速度关系。【母题追问】
1.请根据运动的合成与分解的性质,判断【典例示范】情境中,物体A做什么运动 ( )
A.匀速直线运动 B.匀加速直线运动
C.匀减速直线运动 D.变加速直线运动【解析】选D。物体A的速度为vA= 。由于人匀速
运动,船越往左,θ越大,cosθ越小,vA越大,所以船加
速运动,但并非匀加速直线运动,所以选D。2.请根据运动的合成与分解的性质以及牛顿第二定律,判断【典例示范】情境中,物体A所受的合力 ( )
A.物体A所受的合力为零 B.物体A所受合力向左
C.物体A所受合力向右 D.物体A所受合力不变【解析】选B。物体A的速度为vA= 。
由于人匀速运动,船越往左,θ越大,cosθ越小,vA越大,
所以船加速运动,但并非匀加速直线运动,所以物体A所
受合力向左,是变化的,故选B。【补偿训练】
如图所示,用一小车通过轻绳提升
一货物,某一时刻,两段绳恰好垂直,且
拴在小车一端的绳与水平方向的夹角
为θ,此时小车的速度为v0,则此时货物的速度为( )
A. B.v0sinθ C.v0cosθ D.v0【解析】选D。如图所示,车的速度等于沿绳子方向和垂直于绳子方向速度的合速度,根据平行四边形定则,有v0cosθ=v绳,而货物的速度等于沿绳子方向和垂直于绳子方向速度的合速度。则有v货cos α=v绳。由于两绳子相互垂直,所以α=θ,则由以上两式可得,货物的速度就等于小车的速度。故选D。【拓展例题】考查内容:运动分解的实际应用
【典例】如图,人沿平直的河岸以速度v
行走,且通过不可伸长的绳拖船,船沿绳
的方向行进,此过程中绳始终与水面平行。
当绳与河岸的夹角为α时,船的速率为 ( )
A.vsinα B. C.vcosα D. 【解析】选C。把人的速度v沿着绳子方向和垂直于绳
子方向分解,如图所示。
其中v1=vcosα,所以船的速度等于vcosα。因此C选项
正确。
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
