(新教材)鲁教版物理课件必修二2.4(物理):43张PPT
文档属性
| 名称 | (新教材)鲁教版物理课件必修二2.4(物理):43张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-10-10 00:00:00 | ||
图片预览









文档简介
课件43张PPT。第4节
生活中的抛体运动一、抛体运动
【思考】
(1)抛出的标枪在最高点的速度为零吗?
(2)标枪在竖直方向上的运动情况是怎样的?
提示:(1)最高点速度不为零,但竖直速度为零。
(2)在竖直方向的运动为上抛运动。1.抛体运动的概念:以一定的初速度将物体抛出,物体
仅在_____作用下所做的运动。
2.抛体运动的分类:根据物体抛出的初速度的方向,抛
体运动可分为_________、竖直上抛运动、竖直下抛运
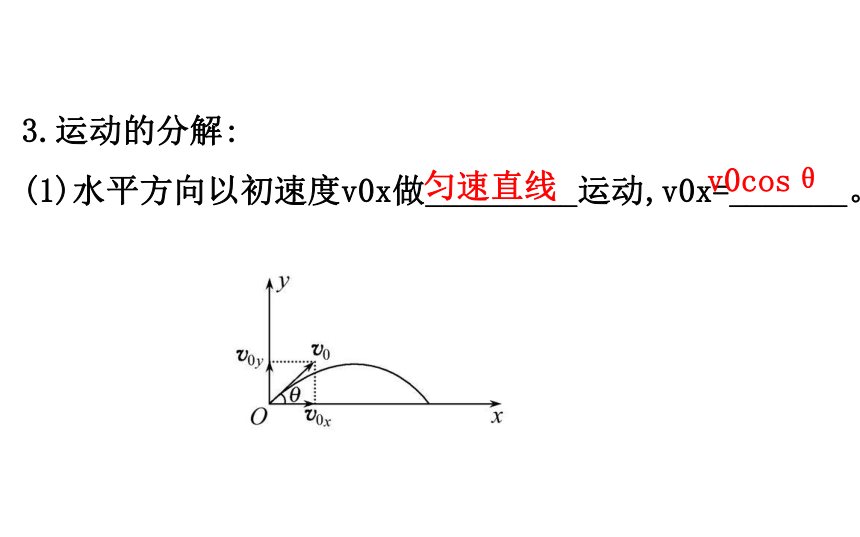
动、_________。重力平抛运动斜抛运动3.运动的分解:
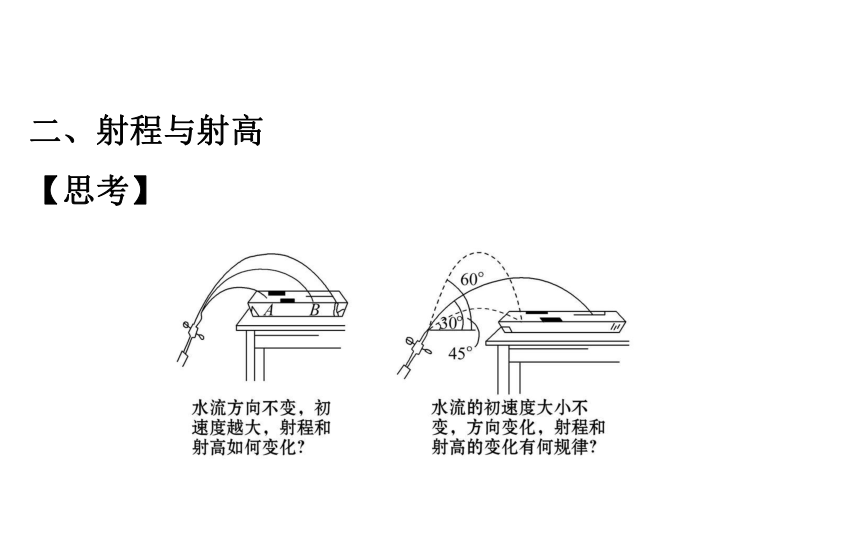
(1)水平方向以初速度v0x做_________运动,v0x=_______。匀速直线v0cosθ(2)竖直方向以初速度v0y做_________运动, v0y=_______。竖直上抛v0sinθ二、射程与射高
【思考】提示:初速度越大,射程和射高都越大;
水流的初速度大小不变时,竖直向上射水时射高最大;方向与水平方向夹角为45°时,射程最大。1.定义:
(1)射高:在斜抛运动中,物体能到达的_________。
(2)射程:物体从抛出点到落地点的_________。
2.射高和射程与初速度和抛射角的关系:
(1)射高和射程与初速度的关系:抛射角一定,初速度
增大时,射程和射高都_____。最大高度水平距离增大(2)射高和射程与抛射角的关系。
初速度大小一定,当抛射角为45°时,射程_____,当抛
射角为_____时,射高最大。
最大90°一 抛体运动的特点
1.受力特点:斜抛运动是忽略了空气阻力的理想化运动,因此物体仅受重力,其加速度为重力加速度g。
2.运动特点:物体具有与水平方向存在夹角的初速度,仅受重力,因此斜抛运动是匀变速曲线运动,其轨迹为抛物线。3.速度变化特点:由于斜抛运动的加速度为定值,因此,在相等的时间内速度的变化大小相等,方向均竖直向下,故相等的时间内速度的变化相同,即Δv=gΔt。
4.对称性特点:
(1)速度对称:相对于轨道最高点两侧对称
的两点速度大小相等或水平方向速度相等,
竖直方向速度等大反向。(如图所示)
(2)时间对称:相对于轨道最高点两侧对称的曲线上升
时间等于下降时间,这是由竖直上抛运动的对称性决定
的。(3)轨迹对称:其运动轨迹关于过最高点的竖直线对称。
【思考·讨论】
如图所示,烟花可以增添欢乐气氛,当然烟
花也蕴含着许多物理知识。假设在高空中
有四个小球,在同一位置同时以速率v竖直
向上、竖直向下、水平向左、水平向右被抛出,不考虑
空气的阻力,经过3 s后四个小球在空中的位置构成的
图形可能什么形状? (物理观念)提示:四个小球所在位置为顶点所构成的图形应该是正方形。
【典例示范】
关于抛体运动,下列说法正确的是
( )
A.抛体运动是一种不受任何外力作用的运动
B.抛体运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
C.任意两段相等时间内的速度变化量相等D.任意两段相等时间内的速度大小变化相等【解析】选C。抛体运动是一种匀变速运动,受重力mg,
故A错;斜抛运动的物体只受重力,因此由牛顿第二定律
可知F=ma,解得a=g;由a= 得Δv=aΔt可知,只要加速
度不变就是匀变速运动,因此抛体运动是匀变速运动,
相等时间内速度变化量相等,故B错C对;速度的变化量
是矢量,满足矢量的合成法则,而速度的大小变化为代
数求和,因此不满足此法则,因此相等时间内速度大小
变化不相等,故D错。【误区警示】抛体运动的两点注意
(1)抛体运动是变速运动,也是匀变速运动。
(2)抛体运动的速度时刻在变化,而加速度保持不变。【素养训练】
1.运动会上,铅球从运动员手中被斜向上推出后在空中飞行的过程中,若不计空气阻力,下列说法正确的是
( )
A.铅球的加速度的大小和方向均不变
B.铅球的加速度的大小不变,方向改变
C.铅球的运动是匀变速直线运动
D.铅球的运动是非匀变速曲线运动【解析】选A。铅球只受重力,根据牛顿第二定律,加速度为重力加速度,保持不变,即铅球的加速度的大小和方向均不变,故A正确,B错误;铅球的运动加速度恒定,但加速度与速度方向不共线,故其做匀变速曲线运动,故C、D错误;故选A。2.斜抛运动可分解为 ( )
A.水平方向的匀速直线运动和竖直方向的自由落体运动
B.水平方向的匀速直线运动和竖直方向的竖直上抛运动
C.水平方向的匀变速直线运动和竖直方向的自由落体运动D.沿初速度方向的匀速直线运动和竖直方向的竖直上抛运动
【解析】选B。若将斜抛运动按水平方向和竖直方向正交分解,两分运动分别为匀速直线运动和竖直上抛运动,故A、C错误,B正确;若沿初速度方向分解出一匀速直线运动,则另一分运动为竖直方向的自由落体运动,故D错误。【补偿训练】
(多选)关于斜抛运动,下列说法正确的是 ( )
A.斜抛运动可以分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动
B.斜抛运动中物体经过最高点时的速度为零
C.斜抛运动中物体经过最高点时的动能最小
D.斜抛运动中物体上升过程中速度逐渐减小【解析】选A、C、D。斜抛运动是水平方向的匀速直线运动和竖直方向的竖直上抛运动的合成,在经过最高点时物体的速度最小,但不为零,故B错误;A、C、D正确。二 抛体运动的规律及应用
1.斜抛运动的规律:
(1)速度规律。
水平速度:vx=v0cosθ。
竖直速度:vy=v0sinθ-gt。
t时刻的速度大小为v= 。(2)位移规律。
水平位移:x=vxt=v0tcosθ。
竖直位移:y=v0tsinθ- gt2。
t时间内的位移大小为s= ,与水平方向成α角,且
tanα= 。2.射高和射程:
(1)斜抛运动的飞行时间:t= 。
(2)射高:h= 。
(3)射程:s=v0cosθ·t= ,
对于给定的v0,当θ=45°时,射程达到最大值,smax=
。【思考·讨论】
在某次跳投表演中,篮球以与水平面成45°的倾角落入篮筐,设投球点和篮筐正好在同一水平面上,如图所示。已知投球点到篮筐距离为10 m,不考虑空气阻力,则篮球投出后的最高点相对篮筐的竖直高度为多少? (物理观念)
提示:篮球抛出后做斜上抛运动,根据对称性可知,出手
时的速度方向与水平方向成45°角,设初速度为v0,则
水平方向x=v0cos45°t;竖直方向设能到达的最大高度
为h,则h= ,解得h= =2.5 m。【典例示范】
以与水平方向成θ角的初速度v0从水平地面上抛出一个小球,不计空气阻力和浮力。若v0一定,则当θ为多大时,射高最大,且求最大的射高;当θ为多大时,射程最大,且求最大的射程。 【解析】如图所示,将v0沿水平方向和竖直方向分解,
得v1=v0sinθ, ①
v2=v0cosθ。 ②小球在竖直方向上以初速度v1做竖直上抛运动,从抛出
点到最高点,有02- =2(-g)h。 ③
从抛出点到落地点,有v1t- gt2=0 ④
由①、③式得h= 。 ⑤
由⑤式可知,当θ=90°时,射高最大,最大的射高Hm=
。小球在水平方向上以速度v2做匀速运动,有
x=v2t ⑥
由①、④式得t= (t=0舍去) ⑦
由②、⑥、⑦式得x= ⑧
由⑧式可知,当θ=45°时,射程最大,最大的射程为
xm= 。
答案:见解析【误区警示】斜抛运动的两点注意事项
(1)做斜抛运动的物体,水平方向不受外力,故做匀速直线运动,竖直方向只受重力且有初速度,故做竖直上抛运动。
(2)在斜抛运动的最高点速度不等于零,等于v0cos θ,加速度也不等于零,而是g。【母题追问】
1.在【典例示范】情境中,当射高最大时,射程是( )
(物理观念)
【解析】选A。当射高最大时,θ为90°,实际为竖直上
抛运动,射程为0,故选A。2.在【典例示范】情境中,当射程最大时,射高是( )
(物理观念)
【解析】选D。当射程最大时,θ为45°,根据【典例示
范】的图示02-(v0sinθ)2=2(-g)h,所以h= ;
故选D。【拓展例题】考查内容:斜抛运动在生活中的应用
【典例】如图所示,打高尔夫球的人
在发球处(该处比球洞所在处低4 m)
击球,该球初速度为35 m/s,方向与
水平方向成37°角。问:把球打向球洞处时,球在水平
方向上前进多远?(忽略空气阻力,g取10 m/s2)【解析】该球初速度的水平分量和竖直分量分别为v0x=v0cos37°=35×0.8 m/s=28 m/s
v0y=v0sin37°=35×0.6 m/s=21 m/s
在竖直方向上,y=v0yt- gt2代入已知量,整理可得5t2-21t+4=0,解得t=0.2 s或4 s,其中t=0.2 s是对应图中B点的解,表示该球自由飞行至B点所需时间。因此本题中,应选解t=4 s。在此飞行时间内,该球的水平初速度不变,可得水平位移为x=v0xt=
28×4 m=112 m。
答案:112 m【课堂回眸】
生活中的抛体运动一、抛体运动
【思考】
(1)抛出的标枪在最高点的速度为零吗?
(2)标枪在竖直方向上的运动情况是怎样的?
提示:(1)最高点速度不为零,但竖直速度为零。
(2)在竖直方向的运动为上抛运动。1.抛体运动的概念:以一定的初速度将物体抛出,物体
仅在_____作用下所做的运动。
2.抛体运动的分类:根据物体抛出的初速度的方向,抛
体运动可分为_________、竖直上抛运动、竖直下抛运
动、_________。重力平抛运动斜抛运动3.运动的分解:
(1)水平方向以初速度v0x做_________运动,v0x=_______。匀速直线v0cosθ(2)竖直方向以初速度v0y做_________运动, v0y=_______。竖直上抛v0sinθ二、射程与射高
【思考】提示:初速度越大,射程和射高都越大;
水流的初速度大小不变时,竖直向上射水时射高最大;方向与水平方向夹角为45°时,射程最大。1.定义:
(1)射高:在斜抛运动中,物体能到达的_________。
(2)射程:物体从抛出点到落地点的_________。
2.射高和射程与初速度和抛射角的关系:
(1)射高和射程与初速度的关系:抛射角一定,初速度
增大时,射程和射高都_____。最大高度水平距离增大(2)射高和射程与抛射角的关系。
初速度大小一定,当抛射角为45°时,射程_____,当抛
射角为_____时,射高最大。
最大90°一 抛体运动的特点
1.受力特点:斜抛运动是忽略了空气阻力的理想化运动,因此物体仅受重力,其加速度为重力加速度g。
2.运动特点:物体具有与水平方向存在夹角的初速度,仅受重力,因此斜抛运动是匀变速曲线运动,其轨迹为抛物线。3.速度变化特点:由于斜抛运动的加速度为定值,因此,在相等的时间内速度的变化大小相等,方向均竖直向下,故相等的时间内速度的变化相同,即Δv=gΔt。
4.对称性特点:
(1)速度对称:相对于轨道最高点两侧对称
的两点速度大小相等或水平方向速度相等,
竖直方向速度等大反向。(如图所示)
(2)时间对称:相对于轨道最高点两侧对称的曲线上升
时间等于下降时间,这是由竖直上抛运动的对称性决定
的。(3)轨迹对称:其运动轨迹关于过最高点的竖直线对称。
【思考·讨论】
如图所示,烟花可以增添欢乐气氛,当然烟
花也蕴含着许多物理知识。假设在高空中
有四个小球,在同一位置同时以速率v竖直
向上、竖直向下、水平向左、水平向右被抛出,不考虑
空气的阻力,经过3 s后四个小球在空中的位置构成的
图形可能什么形状? (物理观念)提示:四个小球所在位置为顶点所构成的图形应该是正方形。
【典例示范】
关于抛体运动,下列说法正确的是
( )
A.抛体运动是一种不受任何外力作用的运动
B.抛体运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
C.任意两段相等时间内的速度变化量相等D.任意两段相等时间内的速度大小变化相等【解析】选C。抛体运动是一种匀变速运动,受重力mg,
故A错;斜抛运动的物体只受重力,因此由牛顿第二定律
可知F=ma,解得a=g;由a= 得Δv=aΔt可知,只要加速
度不变就是匀变速运动,因此抛体运动是匀变速运动,
相等时间内速度变化量相等,故B错C对;速度的变化量
是矢量,满足矢量的合成法则,而速度的大小变化为代
数求和,因此不满足此法则,因此相等时间内速度大小
变化不相等,故D错。【误区警示】抛体运动的两点注意
(1)抛体运动是变速运动,也是匀变速运动。
(2)抛体运动的速度时刻在变化,而加速度保持不变。【素养训练】
1.运动会上,铅球从运动员手中被斜向上推出后在空中飞行的过程中,若不计空气阻力,下列说法正确的是
( )
A.铅球的加速度的大小和方向均不变
B.铅球的加速度的大小不变,方向改变
C.铅球的运动是匀变速直线运动
D.铅球的运动是非匀变速曲线运动【解析】选A。铅球只受重力,根据牛顿第二定律,加速度为重力加速度,保持不变,即铅球的加速度的大小和方向均不变,故A正确,B错误;铅球的运动加速度恒定,但加速度与速度方向不共线,故其做匀变速曲线运动,故C、D错误;故选A。2.斜抛运动可分解为 ( )
A.水平方向的匀速直线运动和竖直方向的自由落体运动
B.水平方向的匀速直线运动和竖直方向的竖直上抛运动
C.水平方向的匀变速直线运动和竖直方向的自由落体运动D.沿初速度方向的匀速直线运动和竖直方向的竖直上抛运动
【解析】选B。若将斜抛运动按水平方向和竖直方向正交分解,两分运动分别为匀速直线运动和竖直上抛运动,故A、C错误,B正确;若沿初速度方向分解出一匀速直线运动,则另一分运动为竖直方向的自由落体运动,故D错误。【补偿训练】
(多选)关于斜抛运动,下列说法正确的是 ( )
A.斜抛运动可以分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动
B.斜抛运动中物体经过最高点时的速度为零
C.斜抛运动中物体经过最高点时的动能最小
D.斜抛运动中物体上升过程中速度逐渐减小【解析】选A、C、D。斜抛运动是水平方向的匀速直线运动和竖直方向的竖直上抛运动的合成,在经过最高点时物体的速度最小,但不为零,故B错误;A、C、D正确。二 抛体运动的规律及应用
1.斜抛运动的规律:
(1)速度规律。
水平速度:vx=v0cosθ。
竖直速度:vy=v0sinθ-gt。
t时刻的速度大小为v= 。(2)位移规律。
水平位移:x=vxt=v0tcosθ。
竖直位移:y=v0tsinθ- gt2。
t时间内的位移大小为s= ,与水平方向成α角,且
tanα= 。2.射高和射程:
(1)斜抛运动的飞行时间:t= 。
(2)射高:h= 。
(3)射程:s=v0cosθ·t= ,
对于给定的v0,当θ=45°时,射程达到最大值,smax=
。【思考·讨论】
在某次跳投表演中,篮球以与水平面成45°的倾角落入篮筐,设投球点和篮筐正好在同一水平面上,如图所示。已知投球点到篮筐距离为10 m,不考虑空气阻力,则篮球投出后的最高点相对篮筐的竖直高度为多少? (物理观念)
提示:篮球抛出后做斜上抛运动,根据对称性可知,出手
时的速度方向与水平方向成45°角,设初速度为v0,则
水平方向x=v0cos45°t;竖直方向设能到达的最大高度
为h,则h= ,解得h= =2.5 m。【典例示范】
以与水平方向成θ角的初速度v0从水平地面上抛出一个小球,不计空气阻力和浮力。若v0一定,则当θ为多大时,射高最大,且求最大的射高;当θ为多大时,射程最大,且求最大的射程。 【解析】如图所示,将v0沿水平方向和竖直方向分解,
得v1=v0sinθ, ①
v2=v0cosθ。 ②小球在竖直方向上以初速度v1做竖直上抛运动,从抛出
点到最高点,有02- =2(-g)h。 ③
从抛出点到落地点,有v1t- gt2=0 ④
由①、③式得h= 。 ⑤
由⑤式可知,当θ=90°时,射高最大,最大的射高Hm=
。小球在水平方向上以速度v2做匀速运动,有
x=v2t ⑥
由①、④式得t= (t=0舍去) ⑦
由②、⑥、⑦式得x= ⑧
由⑧式可知,当θ=45°时,射程最大,最大的射程为
xm= 。
答案:见解析【误区警示】斜抛运动的两点注意事项
(1)做斜抛运动的物体,水平方向不受外力,故做匀速直线运动,竖直方向只受重力且有初速度,故做竖直上抛运动。
(2)在斜抛运动的最高点速度不等于零,等于v0cos θ,加速度也不等于零,而是g。【母题追问】
1.在【典例示范】情境中,当射高最大时,射程是( )
(物理观念)
【解析】选A。当射高最大时,θ为90°,实际为竖直上
抛运动,射程为0,故选A。2.在【典例示范】情境中,当射程最大时,射高是( )
(物理观念)
【解析】选D。当射程最大时,θ为45°,根据【典例示
范】的图示02-(v0sinθ)2=2(-g)h,所以h= ;
故选D。【拓展例题】考查内容:斜抛运动在生活中的应用
【典例】如图所示,打高尔夫球的人
在发球处(该处比球洞所在处低4 m)
击球,该球初速度为35 m/s,方向与
水平方向成37°角。问:把球打向球洞处时,球在水平
方向上前进多远?(忽略空气阻力,g取10 m/s2)【解析】该球初速度的水平分量和竖直分量分别为v0x=v0cos37°=35×0.8 m/s=28 m/s
v0y=v0sin37°=35×0.6 m/s=21 m/s
在竖直方向上,y=v0yt- gt2代入已知量,整理可得5t2-21t+4=0,解得t=0.2 s或4 s,其中t=0.2 s是对应图中B点的解,表示该球自由飞行至B点所需时间。因此本题中,应选解t=4 s。在此飞行时间内,该球的水平初速度不变,可得水平位移为x=v0xt=
28×4 m=112 m。
答案:112 m【课堂回眸】
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
