【A典演练】第三章 第30课时 切线长定理 习题课件
文档属性
| 名称 | 【A典演练】第三章 第30课时 切线长定理 习题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-11 10:08:32 | ||
图片预览



文档简介
课件13张PPT。 第三单元??圆第 30 课时 切线长定理*北师大版 九年级下册考点 1 利用切线长定理计算
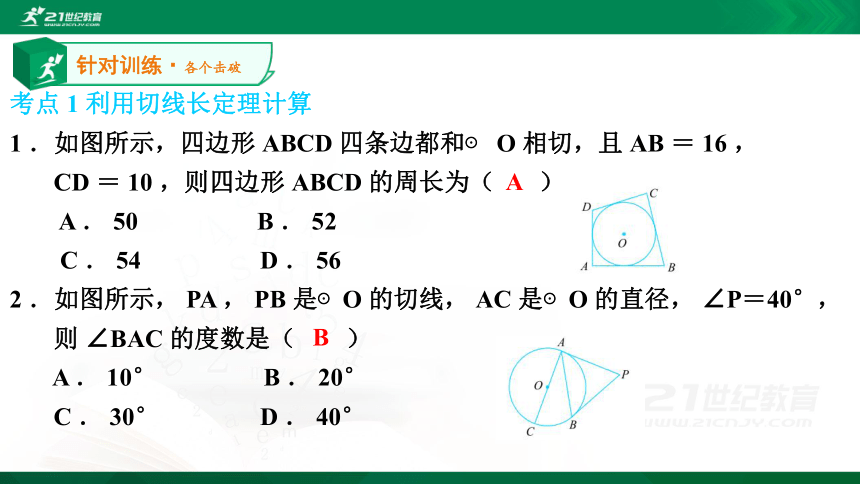
1 .如图所示,四边形 ABCD 四条边都和⊙ O 相切,且 AB = 16 ,
CD = 10 ,则四边形 ABCD 的周长为( )
A . 50 B . 52
C . 54 D . 56
2 .如图所示, PA , PB 是⊙O 的切线, AC 是⊙O 的直径, ∠P=40°,
则 ∠BAC 的度数是( )
A . 10° B . 20°
C . 30° D . 40°针对训练·各个击破AB?针对训练·各个击破412考点 2 利用切线长定理证明
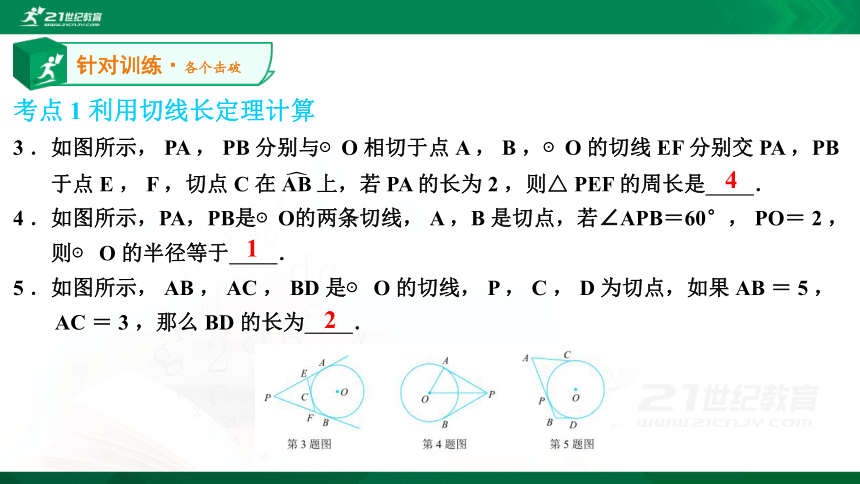
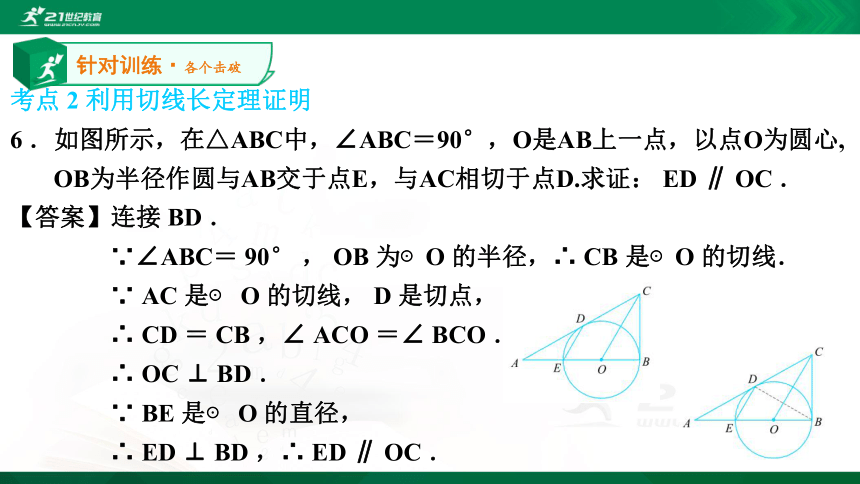
6 .如图所示,在△ABC中,∠ABC=90°,O是AB上一点,以点O为圆心,
OB为半径作圆与AB交于点E,与AC相切于点D.求证: ED ∥ OC .
【答案】连接 BD .
∵∠ABC= 90° , OB 为⊙O 的半径,∴ CB 是⊙O 的切线.
∵ AC 是⊙ O 的切线, D 是切点,
∴ CD = CB ,∠ ACO =∠ BCO .
∴ OC ⊥ BD .
∵ BE 是⊙ O 的直径,
∴ ED ⊥ BD ,∴ ED ∥ OC .针对训练·各个击破?巩固提升·融会贯通?巩固提升·融会贯通8 .如图所示,以Rt△ABC的直角顶点 C 为圆心,作一圆切斜边 AB 于 T ,
过 A ,B 分别作⊙ O 的切线, E , D 为切点.
求证:( 1 ) BD + AE = AB ;
( 2 ) BD ∥ AE .巩固提升·融会贯通【答案】( 1 )连接 CT ,
∵ AE , AB , BD 是⊙ C 的切线,
∴ AE = AT , BT = BD ,
∴ BD + AE = BT + AT = AB ;
( 2 )∵ AE , AB , BD 是⊙ C 的切线,
∴ AC 平分∠ EAB , BC 平分∠ ADB .
又∵∠ ACB = 90° ,
∴∠ CAB +∠ CBA = 90° .
∴∠ EAB +∠ DBA = 180° .
∴ BD ∥ AE .巩固提升·融会贯通9 .如图所示, AB 为⊙O的直径,CB,CD分别切⊙O于点 B , D , CD 交
BA 的延长线于点 E , CO 的延长线交⊙ O 于点 G , EF⊥OG 于点 F .
( 1 )求证:∠ FEB =∠ ECF ;
( 2 )若 BC = 6 , DE = 4 ,求 EF 的长.巩固提升·融会贯通【答案】( 1 )∵ CB , CD 分别切 ⊙O 于点 B , D ,
∴ OC 平分∠ BCE ,即∠ ECO =∠ BCO , OB ⊥ BC .
∴∠ BCO +∠ COB = 90° .
∵ EF ⊥ OG ,
∴∠ FEB +∠ FOE = 90° ,
而∠ COB =∠ FOE ,
∴∠ FEB =∠ ECF .巩固提升·融会贯通?巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1 .如图所示,四边形 ABCD 四条边都和⊙ O 相切,且 AB = 16 ,
CD = 10 ,则四边形 ABCD 的周长为( )
A . 50 B . 52
C . 54 D . 56
2 .如图所示, PA , PB 是⊙O 的切线, AC 是⊙O 的直径, ∠P=40°,
则 ∠BAC 的度数是( )
A . 10° B . 20°
C . 30° D . 40°针对训练·各个击破AB?针对训练·各个击破412考点 2 利用切线长定理证明
6 .如图所示,在△ABC中,∠ABC=90°,O是AB上一点,以点O为圆心,
OB为半径作圆与AB交于点E,与AC相切于点D.求证: ED ∥ OC .
【答案】连接 BD .
∵∠ABC= 90° , OB 为⊙O 的半径,∴ CB 是⊙O 的切线.
∵ AC 是⊙ O 的切线, D 是切点,
∴ CD = CB ,∠ ACO =∠ BCO .
∴ OC ⊥ BD .
∵ BE 是⊙ O 的直径,
∴ ED ⊥ BD ,∴ ED ∥ OC .针对训练·各个击破?巩固提升·融会贯通?巩固提升·融会贯通8 .如图所示,以Rt△ABC的直角顶点 C 为圆心,作一圆切斜边 AB 于 T ,
过 A ,B 分别作⊙ O 的切线, E , D 为切点.
求证:( 1 ) BD + AE = AB ;
( 2 ) BD ∥ AE .巩固提升·融会贯通【答案】( 1 )连接 CT ,
∵ AE , AB , BD 是⊙ C 的切线,
∴ AE = AT , BT = BD ,
∴ BD + AE = BT + AT = AB ;
( 2 )∵ AE , AB , BD 是⊙ C 的切线,
∴ AC 平分∠ EAB , BC 平分∠ ADB .
又∵∠ ACB = 90° ,
∴∠ CAB +∠ CBA = 90° .
∴∠ EAB +∠ DBA = 180° .
∴ BD ∥ AE .巩固提升·融会贯通9 .如图所示, AB 为⊙O的直径,CB,CD分别切⊙O于点 B , D , CD 交
BA 的延长线于点 E , CO 的延长线交⊙ O 于点 G , EF⊥OG 于点 F .
( 1 )求证:∠ FEB =∠ ECF ;
( 2 )若 BC = 6 , DE = 4 ,求 EF 的长.巩固提升·融会贯通【答案】( 1 )∵ CB , CD 分别切 ⊙O 于点 B , D ,
∴ OC 平分∠ BCE ,即∠ ECO =∠ BCO , OB ⊥ BC .
∴∠ BCO +∠ COB = 90° .
∵ EF ⊥ OG ,
∴∠ FEB +∠ FOE = 90° ,
而∠ COB =∠ FOE ,
∴∠ FEB =∠ ECF .巩固提升·融会贯通?巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
