2019苏科版九年级数学下册第5章二次函数 5.1 二次函数同步练习含答案
文档属性
| 名称 | 2019苏科版九年级数学下册第5章二次函数 5.1 二次函数同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 00:00:00 | ||
图片预览


文档简介
第5章 二次函数
知识点:二次函数,二次函数图像与性质,用待定系数法确定解析式,二次函数与一元二次方程,用二次函数解决问题。
典型例题:
例1.在下列各点中,一定在二次函数y=(x?1)2+2图象上的是( )
A.(0,2) B.(1,2) C.(?1,2) D.(1,0)
例2.已知二次函数y=x2?4x+3,当x>0时,函数值y的取值范围是( )
A.y>3 B.y<3 C.y≥?1 D.?1≤y<3
例3.已知抛物线y=ax2+2x+c的顶点坐标为(1,4),则c的值为 .
例4.如图,在抛物线y=x2的内部依次画正方形,使对角线在y轴上,另两个顶点落在抛物线上.按此规律堆垒,第2015个正方形的边长是 .
例5.已知点M(2,1)在二次函数y=ax2?2bx+1的图象上.
(1)b= ;(用含的代数式表示);
(2)该二次函数的图象与x轴的两个交点为A、B,若AB=1,求该二次函数的表达式;
(3)在(2)的条件下,若A(m,y1),B(m+2,y2)两点都在该函数图象上,试探究y1与y2的大小.
例6.如图,抛物线y=x2+bx?4与x轴交于点B(?2,0)和C,点M在y轴上.
(1)求抛物线的解析式;(2)连结BM并延长,交抛物线于点D,过点D作DE⊥BC于点E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
当堂练习:
1.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)2间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是( )
A.2m B.8m C.10m D.12m
2.已知抛物线y=a(x+1)(x-)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有( )
A.2个 B.3个 C.4个 D.5个
3.若二次函数y=ax2+bx+c的x与y的部分对应值如表,则当x=-1时,y的值为 .
4.已知二次函数y=(a-1)x2-2x+l的图像与x轴有两个交点,则a的取值范围是 .
5.已知抛物线y=ax2经过点A(-2,4).
(1)求该抛物线的函数关系式; (2)判断点B(-,-3)是否在此抛物线上;
(3)若图像上有两点M(x1,y1)、N(x2,y2),其中l,则y1 y2(在横线上填“<”“=”或“>”).
6. 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
(1)则A点坐标为 ▲ ;
(2)若点B为该抛物线的顶点,求m、n的值;
(3)在(2)条件下,设该抛物线与x轴的另一个交点为C,请你探索在平面内是否存在点D,使得△DAC与△DCO相似?如果存在,求出点D的坐标;如果不存在,请说明理由.
课后作业:
1.已知函数y=,则自变量x的取值范围是( )
A.x<-1 B.x>-1 C.x≤-1 D.x≥-1
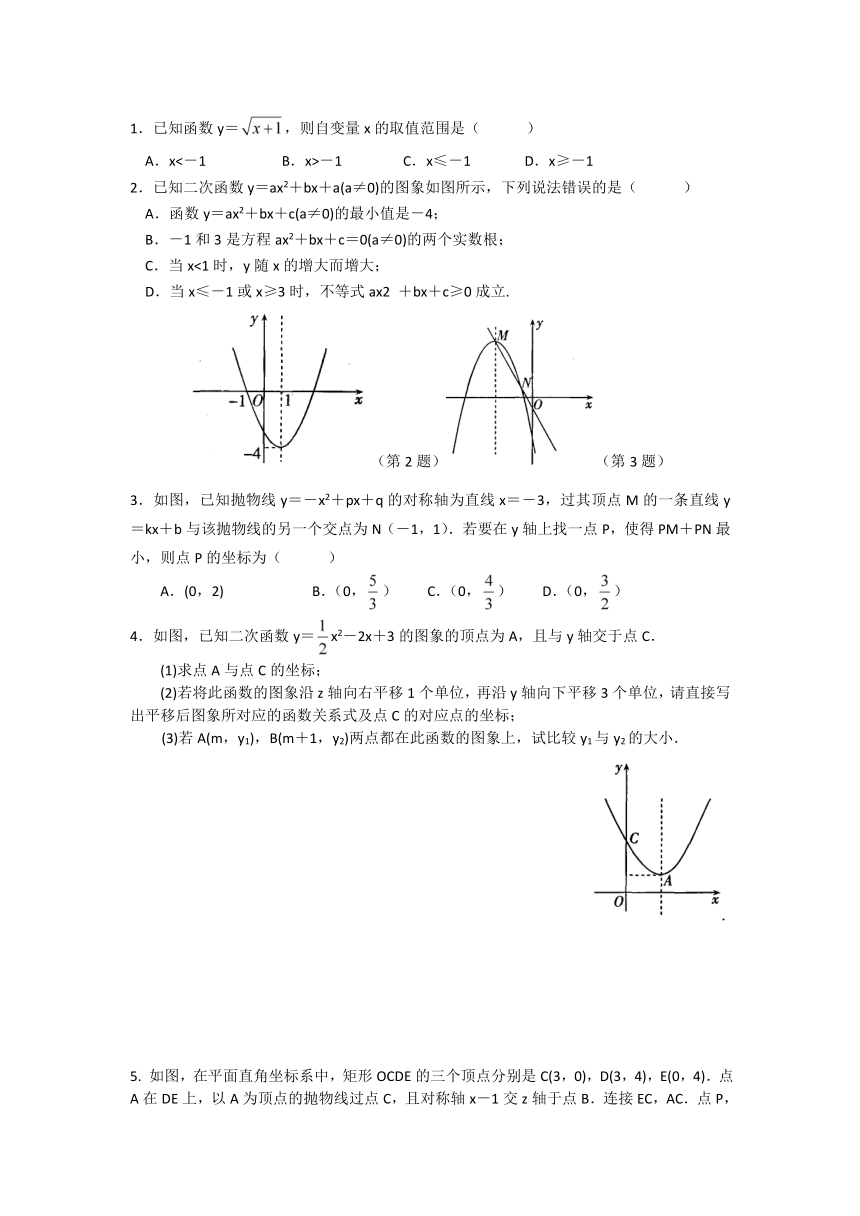
2.已知二次函数y=ax2+bx+a(a≠0)的图象如图所示,下列说法错误的是( )
A.函数y=ax2+bx+c(a≠0)的最小值是-4;
B.-1和3是方程ax2+bx+c=0(a≠0)的两个实数根;
C.当x<1时,y随x的增大而增大;
D.当x≤-1或x≥3时,不等式ax2 +bx+c≥0成立.
(第2题)(第3题)
3.如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
A.(0,2) B.(0,) C.(0,) D.(0,)
4.如图,已知二次函数y=x2-2x+3的图象的顶点为A,且与y轴交于点C.
(1)求点A与点C的坐标;
(2)若将此函数的图象沿z轴向右平移1个单位,再沿y轴向下平移3个单位,请直接写出平移后图象所对应的函数关系式及点C的对应点的坐标;
(3)若A(m,y1),B(m+1,y2)两点都在此函数的图象上,试比较y1与y2的大小.
5. 如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x-1交z轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
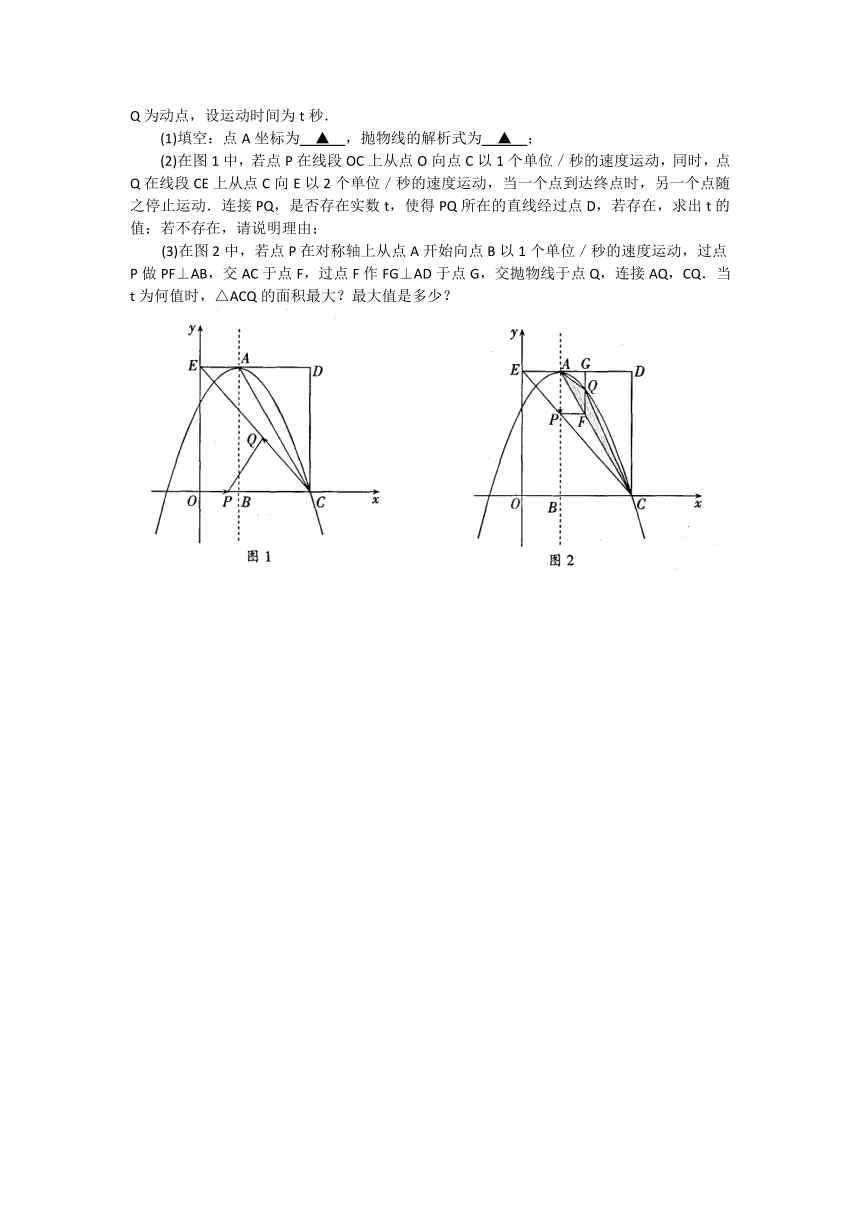
(1)填空:点A坐标为 ▲ ,抛物线的解析式为 ▲ ;
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.连接PQ,是否存在实数t,使得PQ所在的直线经过点D,若存在,求出t的值;若不存在,请说明理由;
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
参考答案:
典型例题:
1、B;2、C;3、3;4、;5、(1) b=a. 2
(2) 抛物线的对称轴为:直线x=1. 3
∵AB=1,∴点(,0)在抛物线上. 4
代入表达式:y=ax2?2ax+1得:a=.即表达式为:y=x2?x+1. 5
(3) ①当m=0时,y1=y2; 6
②当m<0时,y1>y2; 7
③当m>0时,y16. 解:(1)由题意得:0=2?2b?4,解之得:b=?1. 1
∴该函数解析式为:y=x2?x?4. 2
(2)易证:△BOM∽△BED.
∴为使△BDE与△AOC相似,只需△BOM与△AOC相似.
易得:OC=4,OB=2,OA=4,∴△AOC为等腰直角三角形. 4
∴△BOM也为等腰直角三角形.∴M(0,2)或M(0,?2). 6
(3)如图,点M1满足条件∠OM1B+∠OAB=∠ACO.
∵∠ACO=45°,∴∠DBM1=45°.
过点M1作M1D⊥AB于点D.
∴DB=DM1.
在Rt△AOB中,易得:AB=,
tan∠BAO=.
设DM1=x,则在Rt△AOB中,
易得:.
解之得:x=.
∴AM1=DM1=10. 8
根据对称性,在y轴负半轴上,OM2=OM1.
∴AM2=OM2?OA=10?4?4=2. 10
当堂练习:
1、 C;2、C;3、-3;4、且;5、
6.
课后作业:
1、 D;2、C;3、A;4、
5.
A
B
O
C
x
y
A
B
O
C
x
y
M1
D
知识点:二次函数,二次函数图像与性质,用待定系数法确定解析式,二次函数与一元二次方程,用二次函数解决问题。
典型例题:
例1.在下列各点中,一定在二次函数y=(x?1)2+2图象上的是( )
A.(0,2) B.(1,2) C.(?1,2) D.(1,0)
例2.已知二次函数y=x2?4x+3,当x>0时,函数值y的取值范围是( )
A.y>3 B.y<3 C.y≥?1 D.?1≤y<3
例3.已知抛物线y=ax2+2x+c的顶点坐标为(1,4),则c的值为 .
例4.如图,在抛物线y=x2的内部依次画正方形,使对角线在y轴上,另两个顶点落在抛物线上.按此规律堆垒,第2015个正方形的边长是 .
例5.已知点M(2,1)在二次函数y=ax2?2bx+1的图象上.
(1)b= ;(用含的代数式表示);
(2)该二次函数的图象与x轴的两个交点为A、B,若AB=1,求该二次函数的表达式;
(3)在(2)的条件下,若A(m,y1),B(m+2,y2)两点都在该函数图象上,试探究y1与y2的大小.
例6.如图,抛物线y=x2+bx?4与x轴交于点B(?2,0)和C,点M在y轴上.
(1)求抛物线的解析式;(2)连结BM并延长,交抛物线于点D,过点D作DE⊥BC于点E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
当堂练习:
1.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)2间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是( )
A.2m B.8m C.10m D.12m
2.已知抛物线y=a(x+1)(x-)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有( )
A.2个 B.3个 C.4个 D.5个
3.若二次函数y=ax2+bx+c的x与y的部分对应值如表,则当x=-1时,y的值为 .
4.已知二次函数y=(a-1)x2-2x+l的图像与x轴有两个交点,则a的取值范围是 .
5.已知抛物线y=ax2经过点A(-2,4).
(1)求该抛物线的函数关系式; (2)判断点B(-,-3)是否在此抛物线上;
(3)若图像上有两点M(x1,y1)、N(x2,y2),其中l,则y1 y2(在横线上填“<”“=”或“>”).
6. 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
(1)则A点坐标为 ▲ ;
(2)若点B为该抛物线的顶点,求m、n的值;
(3)在(2)条件下,设该抛物线与x轴的另一个交点为C,请你探索在平面内是否存在点D,使得△DAC与△DCO相似?如果存在,求出点D的坐标;如果不存在,请说明理由.
课后作业:
1.已知函数y=,则自变量x的取值范围是( )
A.x<-1 B.x>-1 C.x≤-1 D.x≥-1
2.已知二次函数y=ax2+bx+a(a≠0)的图象如图所示,下列说法错误的是( )
A.函数y=ax2+bx+c(a≠0)的最小值是-4;
B.-1和3是方程ax2+bx+c=0(a≠0)的两个实数根;
C.当x<1时,y随x的增大而增大;
D.当x≤-1或x≥3时,不等式ax2 +bx+c≥0成立.
(第2题)(第3题)
3.如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
A.(0,2) B.(0,) C.(0,) D.(0,)
4.如图,已知二次函数y=x2-2x+3的图象的顶点为A,且与y轴交于点C.
(1)求点A与点C的坐标;
(2)若将此函数的图象沿z轴向右平移1个单位,再沿y轴向下平移3个单位,请直接写出平移后图象所对应的函数关系式及点C的对应点的坐标;
(3)若A(m,y1),B(m+1,y2)两点都在此函数的图象上,试比较y1与y2的大小.
5. 如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x-1交z轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ▲ ,抛物线的解析式为 ▲ ;
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.连接PQ,是否存在实数t,使得PQ所在的直线经过点D,若存在,求出t的值;若不存在,请说明理由;
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
参考答案:
典型例题:
1、B;2、C;3、3;4、;5、(1) b=a. 2
(2) 抛物线的对称轴为:直线x=1. 3
∵AB=1,∴点(,0)在抛物线上. 4
代入表达式:y=ax2?2ax+1得:a=.即表达式为:y=x2?x+1. 5
(3) ①当m=0时,y1=y2; 6
②当m<0时,y1>y2; 7
③当m>0时,y1
∴该函数解析式为:y=x2?x?4. 2
(2)易证:△BOM∽△BED.
∴为使△BDE与△AOC相似,只需△BOM与△AOC相似.
易得:OC=4,OB=2,OA=4,∴△AOC为等腰直角三角形. 4
∴△BOM也为等腰直角三角形.∴M(0,2)或M(0,?2). 6
(3)如图,点M1满足条件∠OM1B+∠OAB=∠ACO.
∵∠ACO=45°,∴∠DBM1=45°.
过点M1作M1D⊥AB于点D.
∴DB=DM1.
在Rt△AOB中,易得:AB=,
tan∠BAO=.
设DM1=x,则在Rt△AOB中,
易得:.
解之得:x=.
∴AM1=DM1=10. 8
根据对称性,在y轴负半轴上,OM2=OM1.
∴AM2=OM2?OA=10?4?4=2. 10
当堂练习:
1、 C;2、C;3、-3;4、且;5、
6.
课后作业:
1、 D;2、C;3、A;4、
5.
A
B
O
C
x
y
A
B
O
C
x
y
M1
D
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
