4.1.2 等式的基本性质学案
图片预览

文档简介
第四章 一元一次方程
1 等式与方程
第2课时 等式的基本性质
自主预习
等式的性质:
1.性质1:等式两边加(或减)_____________(或___________),结果仍相等。
用式子表示:如果a=b,那么a±c=b____________。
2.性质2:等式的两边乘____________,或除以_____________,结果仍相等。
用式子表示:如果a=b,那么ac=_____________;如果a=b,那么__________(c≠0)。
课堂巩固
知识点1:等式性质
1.已知x=y,则下面变形错误的是( )
A.x+a=y+a B.x-a=y-a C.2x=2y D.
2.解方程x-2=3时,应在方程两边( )
A.+2 B.-2 C.+3 D.-3
3.解方程时,应在方程两边同时( )
A.乘-3 B.乘 C.除以3 D.除以
4.下列方程中,解法正确的是( )
A.由0.5x=0,的x=2 B.由-7x=1,得x=-7
C.由,得 D.由0.01x=5,得x=500
5.在等式4y-3=5两边同时___________,得到4y=8;
6.在等式3m=m-2的两边同时___________,得到3m-m=-2.
7.在等式的两边同时___________,得到。
8.在4x-2=1+2x两边都减去____________,得2x-2=1,两边再同时加上__________,得2x=3,变形依据是_____________________________。
9.利用等式的性质解下列一元一次方程。
(1)-4x+2=8;(2)。
课后提升
1.下列变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
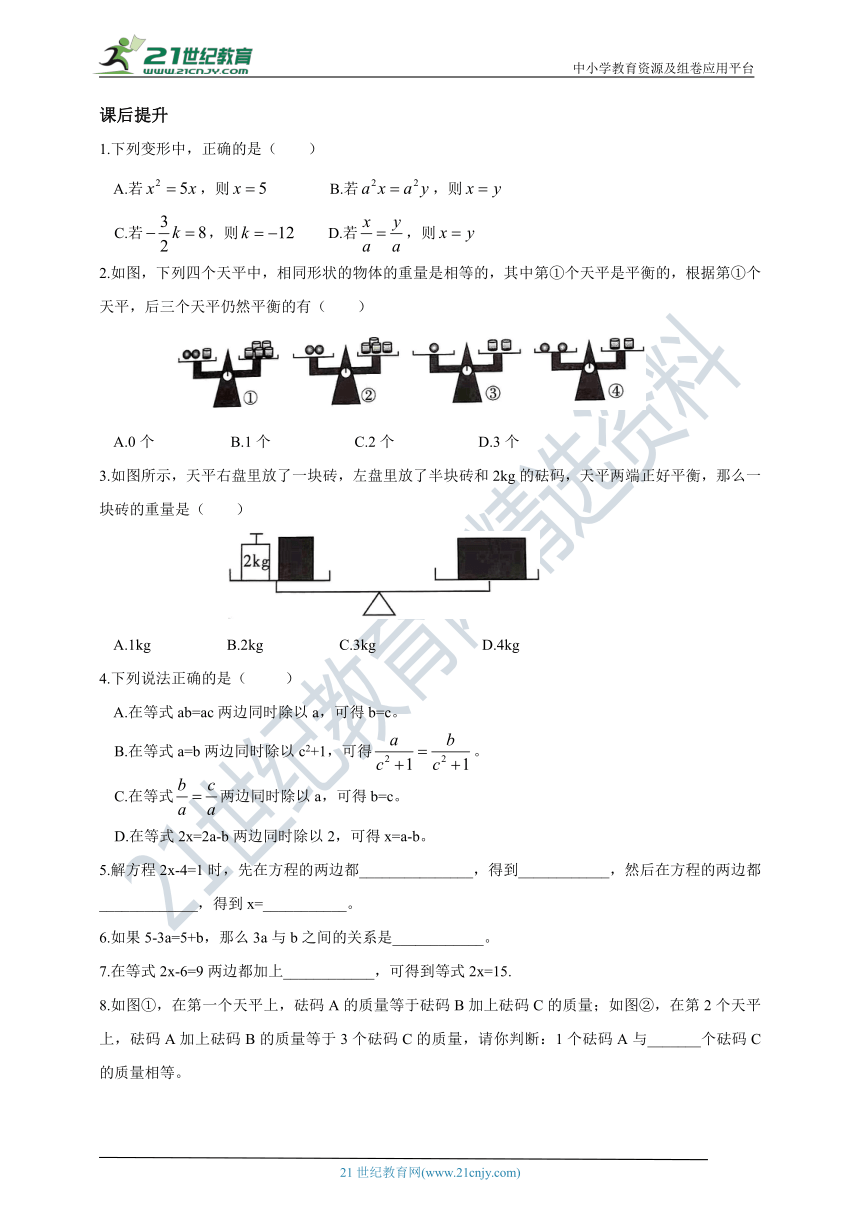
2.如图,下列四个天平中,相同形状的物体的重量是相等的,其中第①个天平是平衡的,根据第①个天平,后三个天平仍然平衡的有( )
A.0个 B.1个 C.2个 D.3个
3.如图所示,天平右盘里放了一块砖,左盘里放了半块砖和2kg的砝码,天平两端正好平衡,那么一块砖的重量是( )
A.1kg B.2kg C.3kg D.4kg
4.下列说法正确的是( )
A.在等式ab=ac两边同时除以a,可得b=c。
B.在等式a=b两边同时除以c2+1,可得。
C.在等式两边同时除以a,可得b=c。
D.在等式2x=2a-b两边同时除以2,可得x=a-b。
5.解方程2x-4=1时,先在方程的两边都_______________,得到____________,然后在方程的两边都_____________,得到x=___________。
6.如果5-3a=5+b,那么3a与b之间的关系是____________。
7.在等式2x-6=9两边都加上____________,可得到等式2x=15.
8.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;如图②,在第2个天平上,砝码A加上砝码B的质量等于3个砝码C的质量,请你判断:1个砝码A与_______个砝码C的质量相等。
9.利用等式的性质解方程:4x+3=5x-5.
10.已知关于x的方程的解为2,求的值。
11.在将等式变形时,小明的变形过程如下:
因为,所以,(第一步)
所以3=2.(第二步)
上述过程中,第一步的依据是什么?
小明第二步得出错误结论的原因是什么?
12.利用等式的性质解方程:
(1); (2)。
创新探究
对于任意有理数a,b,c,d,规定,如,若,试用等式的性质求x的值。
参考答案及解析
自主预习
同一个数 式子 ±c
同一个数 同一个不为0的数 bc
课堂巩固
1.D 2.A 3.A 4.D
5.+3 6.-m 7.乘以 8.2x 2 等式的性质1
9.解:(1)方程的两边同时减2,得-4x=6,方程的两边同时除以-4,得x=。
(2)方程的两边同时加,得即,方程的两边同时除以,得。
课后提升
1.D 2.C 3.D 4.B 5.加上4 2x=5 除以2
6.互为相反数 7.6
8.2 解析:由题意得A=B+C,A+B=3C,解得A=2C,即1个砝码A与2个砝码C的质量相等
9.解:根据等式性质1,在等式的两边同时减3,得4x+3-3=5x-5-3,化简得4x=5x-8.根据等式性质1,在等式的两边同时减5x,得4x-5x=5x-8-5x,化简得-x=-8.根据等式性质2,在等式的两边同时乘以-1,得-x×(-1)=-8×(-1),化简得x=8.
10.解:把x=2代入方程,得即3a=6,解得a=2,所以(-a)2-2a+1=(-2)2-2×2+1=1.
11.解:(1)根据等式性质1,等式两边都加上2b。
(2)等式的两边只有同时除以一个不为0的数,等式才能成立。这里小明在不确定a是否为0的情况下,把方程两边同时除以a而导致出错。
12.解:(1)等式两边同时加上5得:,等式两边同时乘以-3得:x=-27.
(2)等式两边同时加上3-x得:3x-3+3-x=x+1+3-x合并同类项得:2x=4,等式两边同时乘以2得:x=2.
创新探究
13.解:由题意得,-4x-(-2)×3=-2,即-4x+6=-2,两边都减6,得-4x=-8,两边同除以-4,得x=2.
1 等式与方程
第2课时 等式的基本性质
自主预习
等式的性质:
1.性质1:等式两边加(或减)_____________(或___________),结果仍相等。
用式子表示:如果a=b,那么a±c=b____________。
2.性质2:等式的两边乘____________,或除以_____________,结果仍相等。
用式子表示:如果a=b,那么ac=_____________;如果a=b,那么__________(c≠0)。
课堂巩固
知识点1:等式性质
1.已知x=y,则下面变形错误的是( )
A.x+a=y+a B.x-a=y-a C.2x=2y D.
2.解方程x-2=3时,应在方程两边( )
A.+2 B.-2 C.+3 D.-3
3.解方程时,应在方程两边同时( )
A.乘-3 B.乘 C.除以3 D.除以
4.下列方程中,解法正确的是( )
A.由0.5x=0,的x=2 B.由-7x=1,得x=-7
C.由,得 D.由0.01x=5,得x=500
5.在等式4y-3=5两边同时___________,得到4y=8;
6.在等式3m=m-2的两边同时___________,得到3m-m=-2.
7.在等式的两边同时___________,得到。
8.在4x-2=1+2x两边都减去____________,得2x-2=1,两边再同时加上__________,得2x=3,变形依据是_____________________________。
9.利用等式的性质解下列一元一次方程。
(1)-4x+2=8;(2)。
课后提升
1.下列变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,下列四个天平中,相同形状的物体的重量是相等的,其中第①个天平是平衡的,根据第①个天平,后三个天平仍然平衡的有( )
A.0个 B.1个 C.2个 D.3个
3.如图所示,天平右盘里放了一块砖,左盘里放了半块砖和2kg的砝码,天平两端正好平衡,那么一块砖的重量是( )
A.1kg B.2kg C.3kg D.4kg
4.下列说法正确的是( )
A.在等式ab=ac两边同时除以a,可得b=c。
B.在等式a=b两边同时除以c2+1,可得。
C.在等式两边同时除以a,可得b=c。
D.在等式2x=2a-b两边同时除以2,可得x=a-b。
5.解方程2x-4=1时,先在方程的两边都_______________,得到____________,然后在方程的两边都_____________,得到x=___________。
6.如果5-3a=5+b,那么3a与b之间的关系是____________。
7.在等式2x-6=9两边都加上____________,可得到等式2x=15.
8.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;如图②,在第2个天平上,砝码A加上砝码B的质量等于3个砝码C的质量,请你判断:1个砝码A与_______个砝码C的质量相等。
9.利用等式的性质解方程:4x+3=5x-5.
10.已知关于x的方程的解为2,求的值。
11.在将等式变形时,小明的变形过程如下:
因为,所以,(第一步)
所以3=2.(第二步)
上述过程中,第一步的依据是什么?
小明第二步得出错误结论的原因是什么?
12.利用等式的性质解方程:
(1); (2)。
创新探究
对于任意有理数a,b,c,d,规定,如,若,试用等式的性质求x的值。
参考答案及解析
自主预习
同一个数 式子 ±c
同一个数 同一个不为0的数 bc
课堂巩固
1.D 2.A 3.A 4.D
5.+3 6.-m 7.乘以 8.2x 2 等式的性质1
9.解:(1)方程的两边同时减2,得-4x=6,方程的两边同时除以-4,得x=。
(2)方程的两边同时加,得即,方程的两边同时除以,得。
课后提升
1.D 2.C 3.D 4.B 5.加上4 2x=5 除以2
6.互为相反数 7.6
8.2 解析:由题意得A=B+C,A+B=3C,解得A=2C,即1个砝码A与2个砝码C的质量相等
9.解:根据等式性质1,在等式的两边同时减3,得4x+3-3=5x-5-3,化简得4x=5x-8.根据等式性质1,在等式的两边同时减5x,得4x-5x=5x-8-5x,化简得-x=-8.根据等式性质2,在等式的两边同时乘以-1,得-x×(-1)=-8×(-1),化简得x=8.
10.解:把x=2代入方程,得即3a=6,解得a=2,所以(-a)2-2a+1=(-2)2-2×2+1=1.
11.解:(1)根据等式性质1,等式两边都加上2b。
(2)等式的两边只有同时除以一个不为0的数,等式才能成立。这里小明在不确定a是否为0的情况下,把方程两边同时除以a而导致出错。
12.解:(1)等式两边同时加上5得:,等式两边同时乘以-3得:x=-27.
(2)等式两边同时加上3-x得:3x-3+3-x=x+1+3-x合并同类项得:2x=4,等式两边同时乘以2得:x=2.
创新探究
13.解:由题意得,-4x-(-2)×3=-2,即-4x+6=-2,两边都减6,得-4x=-8,两边同除以-4,得x=2.
