人教版八年级数学上册12.2 三角形全等的判定 同步练习(解析版)
文档属性
| 名称 | 人教版八年级数学上册12.2 三角形全等的判定 同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 00:00:00 | ||
图片预览

文档简介
12.2 三角形全等的判定
基础题
1.如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是
A.SAS B.ASA C.HL D.AAS
2.如图,若∠ABC=∠DCB,当添加下列条件时,仍不能判断△ABC≌△DCB的是
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
3.如图,点在的边上,用尺规作出了,作图痕迹中,是
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
4.下列条件中能作出唯一三角形的是
A.AB=4 cm,BC=3 cm,AC=5 cm B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.∠A=30°,∠B=60°,∠C=90°
5.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中,要使DC=AB,则AO、BO、CO、DO应满足下列的条件是
A.AO=CO B.AO=CO且BO=DO
C.AC=BD D.BO=DO
6.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出
A.2个 B.4个 C.6个 D.8个
7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC=__________.
8.如图,中,,,点D为AB的中点,点P在线段BC上以的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动,若点Q的移动速度与点P的移动速度相同,则经过__________秒后,≌.
9.如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌
△CEB.
10.我们把两组邻边相等的四边形叫做“筝形”.如图所示四边形ABCD是一个筝形,其中AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证:OE=OF.
11.如图,AB=AC,AD=AE,CD=BE.求证:∠DAB=∠EAC.
12.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
13.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌ΔDEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
能力题
14.如图,D?E?F分别为△ABC边AC?AB?BC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是
A.AE=FC B.AE=DE C.AE+FC=AC D.AD+FC=AB
15.已知两角及其夹边作三角形,所用的基本作图方法是
A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
16.如图,在四边形中,,,,,则图中的全等三角形有
A.2对 B.3对 C.4对 D.5对
17.如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=
A. B. C. D.
18.如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是__________.
19.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30 m,则河宽为___________.
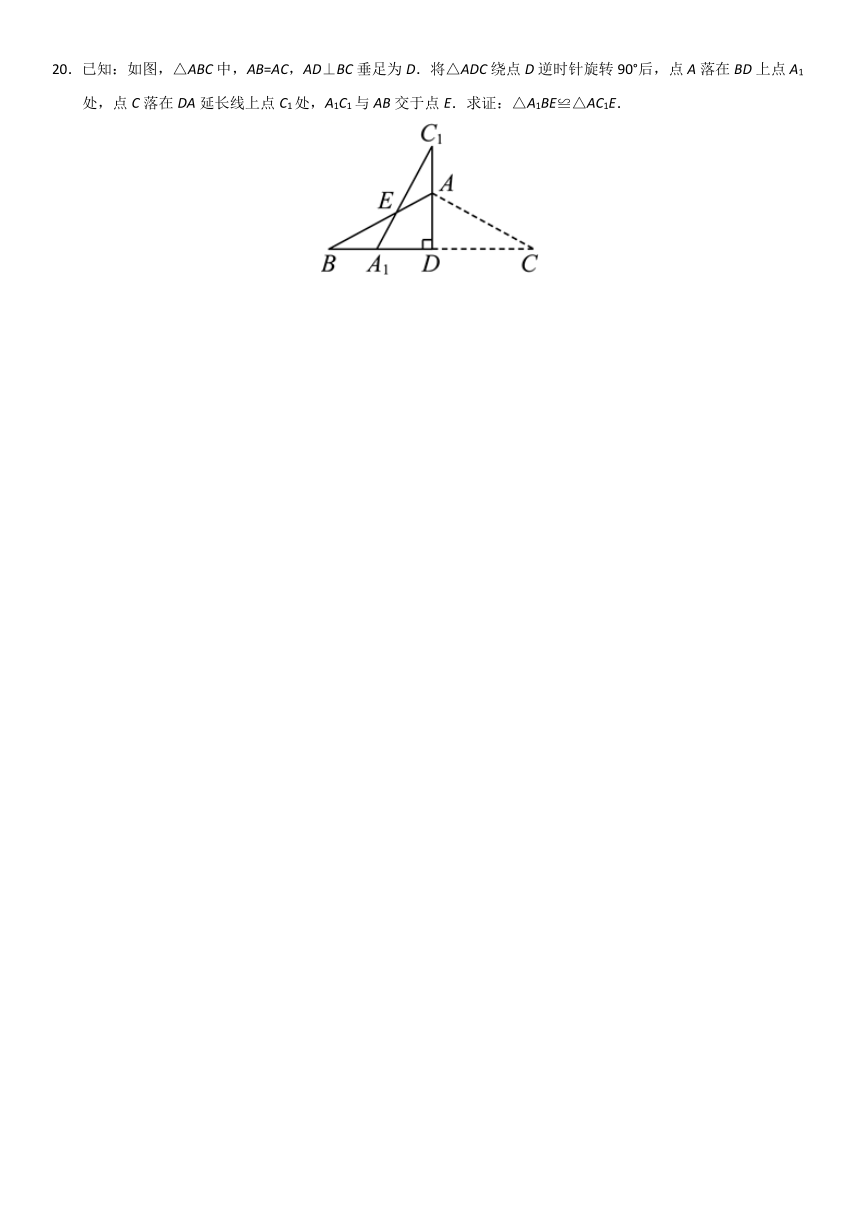
20.已知:如图,△ABC中,AB=AC,AD⊥BC垂足为D.将△ADC绕点D逆时针旋转90°后,点A落在BD上点A1处,点C落在DA延长线上点C1处,A1C1与AB交于点E.求证:△A1BE≌△AC1E.
参考答案
1.【答案】C
【解析】∵Rt△APB和Rt△APC中,,∴Rt△APB≌Rt△APC(HL).故选C.
2.【答案】D
【解析】A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.故选D.
3.【答案】D
【解析】根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选D.
4.【答案】A
【解析】A.符合全等三角形的SSS,能作出唯一三角形,故该选项符合题意,
B.AB+AC=BC,不符合三角形三边之间的关系,不能作出三角形;故该选项不符合题意,
C.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
D.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
故选A.
5.【答案】B
【解析】如图,连接CD.
AO=CO且BO=DO,(对顶角相等),所以,则DC=AB.故选B.
6.【答案】B
【解析】如图,可以作4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.故选B.
7.【答案】
【解析】如图,过D作FD⊥CD交AC于F,连接BF.
∵∠ACD=45°,∴∠CFD=45°,∴FD=CD.
∵∠CDF=∠ADB=90°,∴∠CDA=∠FDB.
在△ADC和△BDF中,∵CD=DF,∠CDA=∠FDB,AD=DB,
∴△ADC≌△BDF,∴∠ACD=∠BFD=45°,AC=BF.
∵∠CFD=45°,∴∠BFC=90°,∴BF⊥AC,∴S△ABC=AC?BF=×5×5=.故答案为:.
8.【答案】1
【解析】∵AB=AC,∴∠B=∠C,
设点P、Q的运动时间为t,则BP=3t,CQ=3t,
∵AB=10 cm,BC=8 cm,点D为AB的中点,
∴BD=×10=5 cm,PC=(8-3t)cm,
∵△BPD≌△CQP,
∴BD=PC,BP=CQ,
∴5=8-3t且3t=3t,
解得t=1,
故答案为:1.
9.【解析】∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB-∠ACE=∠DCE-∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中,,
∴△CDA≌△CEB.
10.【解析】∵在△ABD和△CBD中,AB=CB,AD=CD,BD=BD,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∴BD平分∠ABC.
又∵OE⊥AB,OF⊥CB,
∴OE=OF.
11.【解析】在△ADC和△AEB中,,
∴△ADC≌△AEB(SSS),
∴∠DAC=∠EAB,
∴∠DAC-∠BAC=∠EAB-∠BAC,即∠DAB=∠EAC.
12.【解析】∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,BF=CE,AB=CD,
∴Rt△ABF≌Rt△DCE(HL).
13.【解析】(1)∵AC=AD+DC,DF=DC+CF,且AD=CF,
∴AC=DF.
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS).
(2)由(1)可知,∠F=∠ACB,
∵∠A=55°,∠B=88°,
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°,
∴∠F=∠ACB=37°.
14.【答案】C
【解析】∵∠A+∠AED+∠ADE=180°,∠ADE+∠1+∠CDF=180°,∠A=∠1,
∴∠AED+∠ADE=∠ADE+∠CDF,∴∠AED=∠CDF,
又∵∠A=∠C,DE=DF,
∴△ADE≌△CFD,∴AE=CD,AD=CF,
又∵AD+CD=AC,∴AE+FC=AC,
∴上述四个结论中,正确的是C中的结论,其余三个结论都是错误的,故选C.
15.【答案】C
【解析】已知两角及其夹边作三角形,可先作一条线段等于已知线段,再在线段的两个端点分别作两个角等于已知角,故所用的基本作图方法是作一个角等于已知角及作一条线段等于已知线段.
故选C.
16.【答案】C
【解析】在△AOB和△COD中,OA=OC,OB=OD,∠AOB=∠COD,∴△AOB≌△COD,
同理可证△AOD≌△COB,在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB,
同理可证△ABC≌△DCA,故选C.
17.【答案】C
【解析】∵∠ADB=∠AEC=100°,∴∠ADE=∠AED=80°,∴AD=AE,
∵∠BAD=50°,∴∠B=180°-100°-50°=30°,
在△ADB与△AEC中,,
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴∠B=∠C=30°,
故选C.
18.【答案】7【解析】如图,延长AD到E,使得DE=AD=5,连接EC.
∵AD=DE,∠ADB=∠EDC,BD=DC,∴△ADB≌△EDC,
∴EC=AB,∴,即,.
故答案为:.
19.【答案】30 m
【解析】由题意得:在和中,,∴,
∴,故答案为:30 m.
20.【解析】∵△ABC中,AB=AC,AD⊥BC,
∴∠B=∠C,BD=CD,
∵△A1DC1是由△ADC旋转而得,
∴A1D=AD,C1D=CD,∠C1=∠C,
∴∠B=∠C1,BD=C1D,
∴BD-A1D=C1D-AD,即BA1=C1A.
在△A1BE和△AC1E中,,
∴△A1BE≌△AC1E(AAS).
基础题
1.如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是
A.SAS B.ASA C.HL D.AAS
2.如图,若∠ABC=∠DCB,当添加下列条件时,仍不能判断△ABC≌△DCB的是
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
3.如图,点在的边上,用尺规作出了,作图痕迹中,是
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
4.下列条件中能作出唯一三角形的是
A.AB=4 cm,BC=3 cm,AC=5 cm B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.∠A=30°,∠B=60°,∠C=90°
5.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中,要使DC=AB,则AO、BO、CO、DO应满足下列的条件是
A.AO=CO B.AO=CO且BO=DO
C.AC=BD D.BO=DO
6.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出
A.2个 B.4个 C.6个 D.8个
7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC=__________.
8.如图,中,,,点D为AB的中点,点P在线段BC上以的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动,若点Q的移动速度与点P的移动速度相同,则经过__________秒后,≌.
9.如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌
△CEB.
10.我们把两组邻边相等的四边形叫做“筝形”.如图所示四边形ABCD是一个筝形,其中AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证:OE=OF.
11.如图,AB=AC,AD=AE,CD=BE.求证:∠DAB=∠EAC.
12.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
13.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌ΔDEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
能力题
14.如图,D?E?F分别为△ABC边AC?AB?BC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是
A.AE=FC B.AE=DE C.AE+FC=AC D.AD+FC=AB
15.已知两角及其夹边作三角形,所用的基本作图方法是
A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
16.如图,在四边形中,,,,,则图中的全等三角形有
A.2对 B.3对 C.4对 D.5对
17.如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=
A. B. C. D.
18.如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是__________.
19.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30 m,则河宽为___________.
20.已知:如图,△ABC中,AB=AC,AD⊥BC垂足为D.将△ADC绕点D逆时针旋转90°后,点A落在BD上点A1处,点C落在DA延长线上点C1处,A1C1与AB交于点E.求证:△A1BE≌△AC1E.
参考答案
1.【答案】C
【解析】∵Rt△APB和Rt△APC中,,∴Rt△APB≌Rt△APC(HL).故选C.
2.【答案】D
【解析】A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.故选D.
3.【答案】D
【解析】根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选D.
4.【答案】A
【解析】A.符合全等三角形的SSS,能作出唯一三角形,故该选项符合题意,
B.AB+AC=BC,不符合三角形三边之间的关系,不能作出三角形;故该选项不符合题意,
C.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
D.属于全等三角形判定中的AAA的情况,不能作出唯一三角形;故该选项不符合题意,
故选A.
5.【答案】B
【解析】如图,连接CD.
AO=CO且BO=DO,(对顶角相等),所以,则DC=AB.故选B.
6.【答案】B
【解析】如图,可以作4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.故选B.
7.【答案】
【解析】如图,过D作FD⊥CD交AC于F,连接BF.
∵∠ACD=45°,∴∠CFD=45°,∴FD=CD.
∵∠CDF=∠ADB=90°,∴∠CDA=∠FDB.
在△ADC和△BDF中,∵CD=DF,∠CDA=∠FDB,AD=DB,
∴△ADC≌△BDF,∴∠ACD=∠BFD=45°,AC=BF.
∵∠CFD=45°,∴∠BFC=90°,∴BF⊥AC,∴S△ABC=AC?BF=×5×5=.故答案为:.
8.【答案】1
【解析】∵AB=AC,∴∠B=∠C,
设点P、Q的运动时间为t,则BP=3t,CQ=3t,
∵AB=10 cm,BC=8 cm,点D为AB的中点,
∴BD=×10=5 cm,PC=(8-3t)cm,
∵△BPD≌△CQP,
∴BD=PC,BP=CQ,
∴5=8-3t且3t=3t,
解得t=1,
故答案为:1.
9.【解析】∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB-∠ACE=∠DCE-∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中,,
∴△CDA≌△CEB.
10.【解析】∵在△ABD和△CBD中,AB=CB,AD=CD,BD=BD,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∴BD平分∠ABC.
又∵OE⊥AB,OF⊥CB,
∴OE=OF.
11.【解析】在△ADC和△AEB中,,
∴△ADC≌△AEB(SSS),
∴∠DAC=∠EAB,
∴∠DAC-∠BAC=∠EAB-∠BAC,即∠DAB=∠EAC.
12.【解析】∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,BF=CE,AB=CD,
∴Rt△ABF≌Rt△DCE(HL).
13.【解析】(1)∵AC=AD+DC,DF=DC+CF,且AD=CF,
∴AC=DF.
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS).
(2)由(1)可知,∠F=∠ACB,
∵∠A=55°,∠B=88°,
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°,
∴∠F=∠ACB=37°.
14.【答案】C
【解析】∵∠A+∠AED+∠ADE=180°,∠ADE+∠1+∠CDF=180°,∠A=∠1,
∴∠AED+∠ADE=∠ADE+∠CDF,∴∠AED=∠CDF,
又∵∠A=∠C,DE=DF,
∴△ADE≌△CFD,∴AE=CD,AD=CF,
又∵AD+CD=AC,∴AE+FC=AC,
∴上述四个结论中,正确的是C中的结论,其余三个结论都是错误的,故选C.
15.【答案】C
【解析】已知两角及其夹边作三角形,可先作一条线段等于已知线段,再在线段的两个端点分别作两个角等于已知角,故所用的基本作图方法是作一个角等于已知角及作一条线段等于已知线段.
故选C.
16.【答案】C
【解析】在△AOB和△COD中,OA=OC,OB=OD,∠AOB=∠COD,∴△AOB≌△COD,
同理可证△AOD≌△COB,在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB,
同理可证△ABC≌△DCA,故选C.
17.【答案】C
【解析】∵∠ADB=∠AEC=100°,∴∠ADE=∠AED=80°,∴AD=AE,
∵∠BAD=50°,∴∠B=180°-100°-50°=30°,
在△ADB与△AEC中,,
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴∠B=∠C=30°,
故选C.
18.【答案】7
∵AD=DE,∠ADB=∠EDC,BD=DC,∴△ADB≌△EDC,
∴EC=AB,∴,即,.
故答案为:.
19.【答案】30 m
【解析】由题意得:在和中,,∴,
∴,故答案为:30 m.
20.【解析】∵△ABC中,AB=AC,AD⊥BC,
∴∠B=∠C,BD=CD,
∵△A1DC1是由△ADC旋转而得,
∴A1D=AD,C1D=CD,∠C1=∠C,
∴∠B=∠C1,BD=C1D,
∴BD-A1D=C1D-AD,即BA1=C1A.
在△A1BE和△AC1E中,,
∴△A1BE≌△AC1E(AAS).
