高中物理教科版选修3-1学案 静电场中的图象问题 Word版含答案
文档属性
| 名称 | 高中物理教科版选修3-1学案 静电场中的图象问题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-10-11 10:52:41 | ||
图片预览




文档简介
静电场中的图象问题
静电场中常见的图象问题主要有以下几种类型:1.电场强度随位置变化的图象,即E-x图象;2.电势随位置变化的图象,即φ-x图象;3.电势能随位置变化的图象,即Ep-x图象.解答此类题目的关键是弄清图象的物理意义,即坐标轴、坐标原点、斜率、面积、交点坐标等的物理意义,同时也可以根据图象特点,把抽象的图象转化为具体的电场模型(如匀强电场、点电荷电场、等量同种电荷电场、等量异种电荷电场等),再来分析、解决这类问题.
一、E-x图象
例1有一个均匀带电圆环,以圆环圆心O为坐标原点,过O且垂直于圆环平面的线为x轴,如图甲所示,现测得x轴上的电场强度随坐标x值变化的图象如图乙所示(场强为正值,表示方向沿x轴正方向),H、I是x轴上两点,且HO<OI,取无穷远处电势为零.则以下分析正确的是( )
A.该圆环带负电
B.x轴上O点电势为零
C.将一个正的试探电荷沿x轴从H移动到I的过程中,电势能先增大后减小
D.H点的电势低于I点的电势
【解析】根据x轴上的电场强度随坐标x值变化的图象可知,该圆环带正电,选项A错误;x轴上O点电场强度为零,电势最高,H点的电势高于I点的电势,选项B、D错误.将一个正的试探电荷沿x轴从H移动到I的过程中,电势能先增大后减小,选项C正确.
【答案】C
【归纳总结】1.几种常见的E-x图象
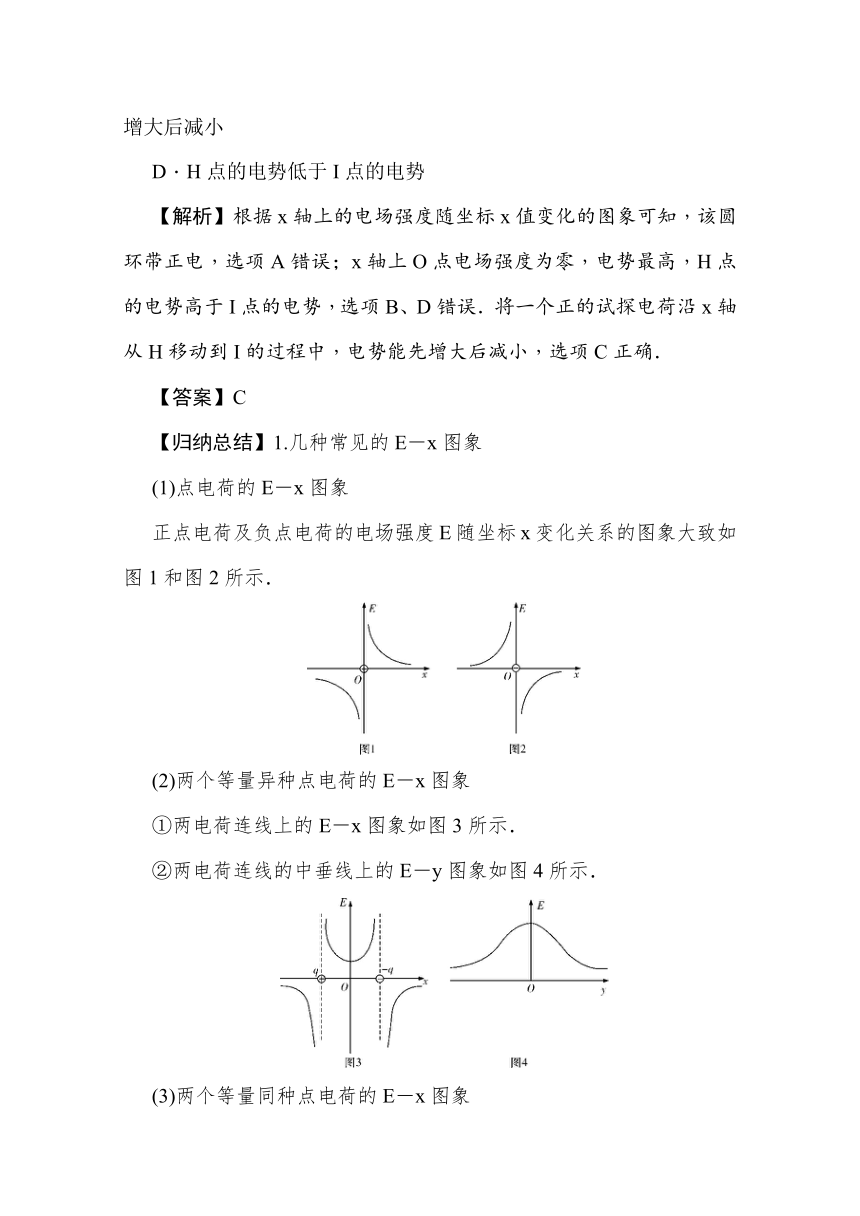
(1)点电荷的E-x图象
正点电荷及负点电荷的电场强度E随坐标x变化关系的图象大致如图1和图2所示.
(2)两个等量异种点电荷的E-x图象
①两电荷连线上的E-x图象如图3所示.
②两电荷连线的中垂线上的E-y图象如图4所示.
(3)两个等量同种点电荷的E-x图象
①两电荷连线上的E-x图象如图5所示.
②两电荷连线的中垂线上的E-y图象如图6所示.
2.E-x图象特点
(1)反映了电场强度随位移变化的规律.
(2)E>0表示场强沿x轴正方向;E<0表示场强沿x轴负方向.
(3)图线与x轴围成的“面积”表示电势差,“面积”大小表示电势差大小,两点的电势高低根据电场方向判定.
二、φ-x图象
例2真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )
A.R处的电场强度E=0
B.若试探电荷从x1处移到x2处,电场力不一定做正功
C.x1处与x2处的电场强度沿x方向的分量的方向相反
D.该电场有可能是处在O点的正的点电荷激发产生的
【解析】φ-x图象中,曲线上任意一点的切线的斜率表示电场强度,R处切线的斜率不为零,故x轴方向的电场强度不为零,故A错误;若试探电荷从x1处移到x2处,电势降低,根据公式WAB=qUAB,如果是正电荷,电场力做正功;如果是负电荷,电场力做负功,故B正确;x1处与x2处的切线斜率同为负值,故x方向的电场强度分量的方向相同,故C错误;离电荷越近,电场强度越大,故φ-x图象的斜率越大,而在O点向右,切线斜率变大,故O点不可能有电荷,故D错误,故选B.
【答案】B
【归纳总结】1.几种常见的φ-x图象
(1)点电荷的φ-x图象(取无限远处电势为零)
①正点电荷的φ-x图象如图1所示;
②负点电荷的φ-x图象如图2所示.
(2)两个等量异种电荷连线上的φ-x图象,如图3所示.
(3)两个等量同种电荷的φ-x图象
①两正电荷连线上的φ-x图象如图4所示.
②两正电荷连线的中垂线上的φ-y图象如图5所示.
2.φ-x图象特点及应用
(1)电场强度的大小等于φ-x图线的斜率大小,电场强度为零处,φ-x图线存在极值,其切线的斜率为零.
(2)在φ-x图象中可以直接判断各点电势的大小,并可根据电势大小关系确定电场强度的方向.
(3)在φ-x图象中分析电荷移动时电势能的变化,可用WAB=qUAB,进而分析WAB的正负,然后作出判断.
三、Ep(Ek)-x图象
例3一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中O~x2段关于直线x=x1对称的曲线,x2~x3段是直线,则下列说法正确的是( )
A.x1处电场强度最小,但不为零
B.粒子在O~x2段做匀变速运动,x2~x3段做匀速直线运动
C.在O、x1、x2、x3处电势φ0、φ1、φ2、φ3的关系为φ3>φ2=φ0>φ1
D.x2~x3段的电场强度大小、方向均不变
【解析】根据电势能与电势的关系Ep=qφ,场强与电势的关系E=,得E=·,由数学知识可知Ep-x图象切线的斜率等于,x1处切线斜率为零,则x1处电场强度为零,A错误;由题图知在O~x1段图象切线斜率的绝对值不断减小,可知场强减小,粒子所受的电场力减小,加速度减小,粒子做变速运动,x1~x2段图象切线的斜率不断增大,场强增大,粒子所受的电场力增大,粒子做变速运动,x2~x3段斜率不变,场强不变,即电场强度大小和方向均不变,是匀强电场,粒子所受的电场力不变,粒子做匀加速直线运动,B错误,D正确;根据Ep=qφ,粒子带负电即q<0,则知电势能越大,粒子所在处的电势越低,所以有φ1>φ2=φ0>φ3,C错误.
【答案】D
【归纳总结】解决此类图象问题的关键是弄清楚电场中的功能关系:电场力做功对应电势能的变化,即W电=-ΔEp=Ep0-Ep,即F电=||,因此图线的斜率表示了电场力的大小,也反映了电场强度的大小,若电场力为恒力,则电场强度不变,则Ep-x图线为一条倾斜直线.
针对训练
1.已知某静电场的电场强度的方向与x轴的正方向一致,电场强度大小E与位置x的关系图象如图所示,其中O~x2段为抛物线的一段且关于x=x1对称,x2~x3段为倾斜的直线,且x1=x2-x1=x3-x2,开始时一带正电粒子位于原点,现给该粒子一水平向右的初速度,使其仅在电场力的作用下沿x轴的正方向运动.则下列说法正确的是(C)
A.带电粒子在O~x2段先做减速运动再做加速运动
B.带电粒子在x2~x3段做匀加速直线运动
C.位置O与x1间的电势差等于位置x1与x2间的电势差
D.在O~x3段电场力对带电粒子一直做负功
【解析】O~x3段电场的方向始终沿x轴的正方向,则该带电粒子所受的电场力一直沿x轴的正方向,粒子一直沿x轴的正方向做加速运动,则电场力一直对该粒子做正功,A、D错误;x2~x3段电场强度沿x轴的正方向逐渐增大,粒子做加速度逐渐增大的加速运动,B错误;根据对称性可知,位置O与x1间的平均电场强度与位置x1与x2间的平均电场强度相等,则由U=Ed可知,位置O与x1间的电势差等于位置x1与x2间的电势差,C正确.
2.(多选)在x轴上存在一水平方向的电场,有一质量m=2 kg的带电小球沿光滑绝缘的水平面只在电场力的作用下,以初速度v0=2 m/s在x0=7 m处开始向x轴负方向运动.电势能Ep随位置x的变化关系如图所示,则小球的运动范围和最大速度分别为(BC)
A.运动范围x≥0
B.运动范围x≥1 m
C.最大速度vm=2 m/s
D.最大速度vm=3 m/s
【解析】根据动能定理可得W电=0-mv=-4 J,故电势能增大4 J,因在开始时电势能为零,故电势能最多增大4 J,故运动范围在x≥1 m,故A错误,B正确;由图可知,电势能最大减小4 J,故动能最多增大4 J,根据动能定理可得W=mv2-mv;解得v=2 m/s,故C正确,D错误.
3.(多选)在光滑的绝缘水平面内有一沿x轴的静电场,其电势φ随坐标x变化的图线如图所示(图中φ0已知).有一质量为m,带电量为q的带负电小球(可视为质点)从O点以某一未知速度v0沿x轴正向移动到点x4.下列叙述正确的是(BC)
A.带电小球从O运动到x1的过程中,所受电场力逐渐增大
B.带电小球从x1运动到x3的过程中,电势能一直增大
C.若小球的初速度v0=2,则运动过程中的最大速度为
D.要使小球能运动到x4处,则初速度v0至少为2
【解析】由E=知,φ-x图象的斜率等于电场强度,则可知小球从O运动到x1的过程中,场强不变,由F=qE知,粒子所受电场力保持不变,故A错误;负电荷在电势高处电势能小,则小球从x1运动到x3的过程中,电势不断降低,负电荷的电势能一直增大,故B正确;若小球的初速度v0=2,当小球运动到x1处时,电场力做正功最多,粒子的速度最大,从x=0到x1处,根据动能定理得:qφ0=mv-mv,由题意,有:v0=2,解得最大速度为:vm=,故C正确;只要小球能恰好运动到x3处,初速度v0最小,就能到x4处,从x=0到x3处,根据动能定理得:qφ0=mv,解得:v0=,故D错误.
4.等量异种点电荷在周围空间产生静电场,其连线(x轴)上各点的电势φ随x的分布图象如图所示.x轴上AOA.φB>φA>φO
B.EA>EO>EB
C.EpOD.EpB-EpO>EpO-EpA
【解析】正电荷周围电势较高,负电荷周围电势较低,φA>φO>φB,A错误;根据电场强度的合成可知B点场强最大,O点最小,B错误;电子带负电,根据电势能Ep=qφ,可知EpB最大,EpA最小,C错误;由图象可知UOB>UAO,根据电场力做功W=qU,电子带负电,可知WBO>WOA,即EpB-EpO>EpO-EpA,D正确.
5.(多选)一带正电粒子在正点电荷的电场中仅受静电力作用,做初速度为零的直线运动.取该直线为x轴,起始点O为坐标原点,则下列关于电场强度E、粒子动能Ek、粒子电势能Ep、粒子加速度a与位移x的关系图象可能的是(CD)
【解析】依点电荷的场强公式E=k,可知电场强度随x的变化不是均匀减小,故A错误;由于不是匀强电场,电场力做功W≠qEx,则动能不是随x均匀增大,故B错误;Ep-x图线的切线斜率表示电场力,随着x的增大,电场力逐渐减小,故C正确;加速度a===,可知a随x的变化图线是曲线,且减小,故D正确.
6.如图所示,矩形区域PQNM内存在平行于纸面的匀强电场,一质量为m、电荷量为q的带正电粒子(重力不计)从a点以v1的初速度垂直于PQ进入电场,最终从MN边界的b点以与水平边界MN成30°角斜向右上方的方向射出,射出电场时的速度v2=2v1,取a点电势为零,如果以a点为坐标原点O,沿PQ方向建立x轴,则粒子从a点运动到b点的过程中,电场的电场强度E、电势φ、粒子的速度v、电势能Ep随x的变化图象正确的是(D)
【解析】因为匀强电场中的电场强度处处相等,故A错误;因为粒子离开电场时y方向的速度vy=v2sin 30°=v1,则电场的方向水平向右,沿电场线的方向电势降低,故B错误;粒子在电场中运动的过程中,由动能定理可知,qEx=mv2-mv,所以v与x不是线性关系,C错误;因为规定a点电势为零,粒子进入电场后做类平抛运动,根据电场力做功与电势能的变化的关系,有qEx=-ΔEp=0-Ep,故Ep=-qEx,故D正确.
7.(多选)真空中有一半径为r0的带电金属球壳,通过其球心的一直线上各点的电势φ分布如图,r表示该直线上某点到球心的距离,r1、r2分别是该直线上A、B两点离球心的距离.下列说法中正确的是(BC)
A.A点的电势低于B点的电势
B.A点的电场强度方向由A指向B
C.A点的电场强度大于B点的电场强度
D.正电荷沿直线从A移到B的过程中,电场力做负功
【解析】A点的电势高于B点的电势,选项A错误;A点的电场强度方向由A指向B,A点的电场强度大于B点的电场强度,选项B、C正确;正电荷沿直线从A移到B的过程中,电场力做正功,选项D错误.
8.(多选)如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3.0)的切线.现有一质量为0.20 kg,电荷量为+2.0×10-8 C的滑块P(可视作质点),从x=0.10 m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10 m/s2.则下列说法正确的是(CD)
A.滑块运动的加速度逐渐减小
B.滑块运动的速度先减小后增大
C.x=0.15 m处的场强大小为2.0×106 N/C
D.滑块运动的最大速度约为0.10 m/s
【解析】根据E==-,在x轴上的电势φ与坐标x的关系图象斜率的大小表示电场强度,电场强度的方向沿x轴的正方向.由电势φ与坐标x的关系图象可知,沿x轴正方向,电场强度越来越小.滑块从x=0.10 m处由静止释放,所受电场力方向沿x轴正方向,所受电场力越来越小,当电场力等于滑动摩擦力时加速度减小到零.滑块继续运动,做减速运动,加速度增大,所以滑块运动的加速度先减小后增大,选项A错误.滑块先做加速运动,后做减速运动,选项B错误.由E=-,可知x=0.15 m处的场强大小为2.0×106 N/C,选项C正确.当滑动摩擦力等于电场力时,滑块运动的速度最大.滑块所受滑动摩擦力f=μmg=0.04 N.由f=qE可得对应点的电场强度E=2.0×106 N/C,对应的x=0.15 m.由动能定理,qU-μmgΔx=mv2,0.1 m处电势约为4.5×105 V,0.15 m处电势为3.0×105 V,∴U=1.5×105 V,解得v=0.1 m/s.即滑块运动的最大速度约为0.1 m/s,选项D正确.
静电场中常见的图象问题主要有以下几种类型:1.电场强度随位置变化的图象,即E-x图象;2.电势随位置变化的图象,即φ-x图象;3.电势能随位置变化的图象,即Ep-x图象.解答此类题目的关键是弄清图象的物理意义,即坐标轴、坐标原点、斜率、面积、交点坐标等的物理意义,同时也可以根据图象特点,把抽象的图象转化为具体的电场模型(如匀强电场、点电荷电场、等量同种电荷电场、等量异种电荷电场等),再来分析、解决这类问题.
一、E-x图象
例1有一个均匀带电圆环,以圆环圆心O为坐标原点,过O且垂直于圆环平面的线为x轴,如图甲所示,现测得x轴上的电场强度随坐标x值变化的图象如图乙所示(场强为正值,表示方向沿x轴正方向),H、I是x轴上两点,且HO<OI,取无穷远处电势为零.则以下分析正确的是( )
A.该圆环带负电
B.x轴上O点电势为零
C.将一个正的试探电荷沿x轴从H移动到I的过程中,电势能先增大后减小
D.H点的电势低于I点的电势
【解析】根据x轴上的电场强度随坐标x值变化的图象可知,该圆环带正电,选项A错误;x轴上O点电场强度为零,电势最高,H点的电势高于I点的电势,选项B、D错误.将一个正的试探电荷沿x轴从H移动到I的过程中,电势能先增大后减小,选项C正确.
【答案】C
【归纳总结】1.几种常见的E-x图象
(1)点电荷的E-x图象
正点电荷及负点电荷的电场强度E随坐标x变化关系的图象大致如图1和图2所示.
(2)两个等量异种点电荷的E-x图象
①两电荷连线上的E-x图象如图3所示.
②两电荷连线的中垂线上的E-y图象如图4所示.
(3)两个等量同种点电荷的E-x图象
①两电荷连线上的E-x图象如图5所示.
②两电荷连线的中垂线上的E-y图象如图6所示.
2.E-x图象特点
(1)反映了电场强度随位移变化的规律.
(2)E>0表示场强沿x轴正方向;E<0表示场强沿x轴负方向.
(3)图线与x轴围成的“面积”表示电势差,“面积”大小表示电势差大小,两点的电势高低根据电场方向判定.
二、φ-x图象
例2真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )
A.R处的电场强度E=0
B.若试探电荷从x1处移到x2处,电场力不一定做正功
C.x1处与x2处的电场强度沿x方向的分量的方向相反
D.该电场有可能是处在O点的正的点电荷激发产生的
【解析】φ-x图象中,曲线上任意一点的切线的斜率表示电场强度,R处切线的斜率不为零,故x轴方向的电场强度不为零,故A错误;若试探电荷从x1处移到x2处,电势降低,根据公式WAB=qUAB,如果是正电荷,电场力做正功;如果是负电荷,电场力做负功,故B正确;x1处与x2处的切线斜率同为负值,故x方向的电场强度分量的方向相同,故C错误;离电荷越近,电场强度越大,故φ-x图象的斜率越大,而在O点向右,切线斜率变大,故O点不可能有电荷,故D错误,故选B.
【答案】B
【归纳总结】1.几种常见的φ-x图象
(1)点电荷的φ-x图象(取无限远处电势为零)
①正点电荷的φ-x图象如图1所示;
②负点电荷的φ-x图象如图2所示.
(2)两个等量异种电荷连线上的φ-x图象,如图3所示.
(3)两个等量同种电荷的φ-x图象
①两正电荷连线上的φ-x图象如图4所示.
②两正电荷连线的中垂线上的φ-y图象如图5所示.
2.φ-x图象特点及应用
(1)电场强度的大小等于φ-x图线的斜率大小,电场强度为零处,φ-x图线存在极值,其切线的斜率为零.
(2)在φ-x图象中可以直接判断各点电势的大小,并可根据电势大小关系确定电场强度的方向.
(3)在φ-x图象中分析电荷移动时电势能的变化,可用WAB=qUAB,进而分析WAB的正负,然后作出判断.
三、Ep(Ek)-x图象
例3一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中O~x2段关于直线x=x1对称的曲线,x2~x3段是直线,则下列说法正确的是( )
A.x1处电场强度最小,但不为零
B.粒子在O~x2段做匀变速运动,x2~x3段做匀速直线运动
C.在O、x1、x2、x3处电势φ0、φ1、φ2、φ3的关系为φ3>φ2=φ0>φ1
D.x2~x3段的电场强度大小、方向均不变
【解析】根据电势能与电势的关系Ep=qφ,场强与电势的关系E=,得E=·,由数学知识可知Ep-x图象切线的斜率等于,x1处切线斜率为零,则x1处电场强度为零,A错误;由题图知在O~x1段图象切线斜率的绝对值不断减小,可知场强减小,粒子所受的电场力减小,加速度减小,粒子做变速运动,x1~x2段图象切线的斜率不断增大,场强增大,粒子所受的电场力增大,粒子做变速运动,x2~x3段斜率不变,场强不变,即电场强度大小和方向均不变,是匀强电场,粒子所受的电场力不变,粒子做匀加速直线运动,B错误,D正确;根据Ep=qφ,粒子带负电即q<0,则知电势能越大,粒子所在处的电势越低,所以有φ1>φ2=φ0>φ3,C错误.
【答案】D
【归纳总结】解决此类图象问题的关键是弄清楚电场中的功能关系:电场力做功对应电势能的变化,即W电=-ΔEp=Ep0-Ep,即F电=||,因此图线的斜率表示了电场力的大小,也反映了电场强度的大小,若电场力为恒力,则电场强度不变,则Ep-x图线为一条倾斜直线.
针对训练
1.已知某静电场的电场强度的方向与x轴的正方向一致,电场强度大小E与位置x的关系图象如图所示,其中O~x2段为抛物线的一段且关于x=x1对称,x2~x3段为倾斜的直线,且x1=x2-x1=x3-x2,开始时一带正电粒子位于原点,现给该粒子一水平向右的初速度,使其仅在电场力的作用下沿x轴的正方向运动.则下列说法正确的是(C)
A.带电粒子在O~x2段先做减速运动再做加速运动
B.带电粒子在x2~x3段做匀加速直线运动
C.位置O与x1间的电势差等于位置x1与x2间的电势差
D.在O~x3段电场力对带电粒子一直做负功
【解析】O~x3段电场的方向始终沿x轴的正方向,则该带电粒子所受的电场力一直沿x轴的正方向,粒子一直沿x轴的正方向做加速运动,则电场力一直对该粒子做正功,A、D错误;x2~x3段电场强度沿x轴的正方向逐渐增大,粒子做加速度逐渐增大的加速运动,B错误;根据对称性可知,位置O与x1间的平均电场强度与位置x1与x2间的平均电场强度相等,则由U=Ed可知,位置O与x1间的电势差等于位置x1与x2间的电势差,C正确.
2.(多选)在x轴上存在一水平方向的电场,有一质量m=2 kg的带电小球沿光滑绝缘的水平面只在电场力的作用下,以初速度v0=2 m/s在x0=7 m处开始向x轴负方向运动.电势能Ep随位置x的变化关系如图所示,则小球的运动范围和最大速度分别为(BC)
A.运动范围x≥0
B.运动范围x≥1 m
C.最大速度vm=2 m/s
D.最大速度vm=3 m/s
【解析】根据动能定理可得W电=0-mv=-4 J,故电势能增大4 J,因在开始时电势能为零,故电势能最多增大4 J,故运动范围在x≥1 m,故A错误,B正确;由图可知,电势能最大减小4 J,故动能最多增大4 J,根据动能定理可得W=mv2-mv;解得v=2 m/s,故C正确,D错误.
3.(多选)在光滑的绝缘水平面内有一沿x轴的静电场,其电势φ随坐标x变化的图线如图所示(图中φ0已知).有一质量为m,带电量为q的带负电小球(可视为质点)从O点以某一未知速度v0沿x轴正向移动到点x4.下列叙述正确的是(BC)
A.带电小球从O运动到x1的过程中,所受电场力逐渐增大
B.带电小球从x1运动到x3的过程中,电势能一直增大
C.若小球的初速度v0=2,则运动过程中的最大速度为
D.要使小球能运动到x4处,则初速度v0至少为2
【解析】由E=知,φ-x图象的斜率等于电场强度,则可知小球从O运动到x1的过程中,场强不变,由F=qE知,粒子所受电场力保持不变,故A错误;负电荷在电势高处电势能小,则小球从x1运动到x3的过程中,电势不断降低,负电荷的电势能一直增大,故B正确;若小球的初速度v0=2,当小球运动到x1处时,电场力做正功最多,粒子的速度最大,从x=0到x1处,根据动能定理得:qφ0=mv-mv,由题意,有:v0=2,解得最大速度为:vm=,故C正确;只要小球能恰好运动到x3处,初速度v0最小,就能到x4处,从x=0到x3处,根据动能定理得:qφ0=mv,解得:v0=,故D错误.
4.等量异种点电荷在周围空间产生静电场,其连线(x轴)上各点的电势φ随x的分布图象如图所示.x轴上AO
B.EA>EO>EB
C.EpO
【解析】正电荷周围电势较高,负电荷周围电势较低,φA>φO>φB,A错误;根据电场强度的合成可知B点场强最大,O点最小,B错误;电子带负电,根据电势能Ep=qφ,可知EpB最大,EpA最小,C错误;由图象可知UOB>UAO,根据电场力做功W=qU,电子带负电,可知WBO>WOA,即EpB-EpO>EpO-EpA,D正确.
5.(多选)一带正电粒子在正点电荷的电场中仅受静电力作用,做初速度为零的直线运动.取该直线为x轴,起始点O为坐标原点,则下列关于电场强度E、粒子动能Ek、粒子电势能Ep、粒子加速度a与位移x的关系图象可能的是(CD)
【解析】依点电荷的场强公式E=k,可知电场强度随x的变化不是均匀减小,故A错误;由于不是匀强电场,电场力做功W≠qEx,则动能不是随x均匀增大,故B错误;Ep-x图线的切线斜率表示电场力,随着x的增大,电场力逐渐减小,故C正确;加速度a===,可知a随x的变化图线是曲线,且减小,故D正确.
6.如图所示,矩形区域PQNM内存在平行于纸面的匀强电场,一质量为m、电荷量为q的带正电粒子(重力不计)从a点以v1的初速度垂直于PQ进入电场,最终从MN边界的b点以与水平边界MN成30°角斜向右上方的方向射出,射出电场时的速度v2=2v1,取a点电势为零,如果以a点为坐标原点O,沿PQ方向建立x轴,则粒子从a点运动到b点的过程中,电场的电场强度E、电势φ、粒子的速度v、电势能Ep随x的变化图象正确的是(D)
【解析】因为匀强电场中的电场强度处处相等,故A错误;因为粒子离开电场时y方向的速度vy=v2sin 30°=v1,则电场的方向水平向右,沿电场线的方向电势降低,故B错误;粒子在电场中运动的过程中,由动能定理可知,qEx=mv2-mv,所以v与x不是线性关系,C错误;因为规定a点电势为零,粒子进入电场后做类平抛运动,根据电场力做功与电势能的变化的关系,有qEx=-ΔEp=0-Ep,故Ep=-qEx,故D正确.
7.(多选)真空中有一半径为r0的带电金属球壳,通过其球心的一直线上各点的电势φ分布如图,r表示该直线上某点到球心的距离,r1、r2分别是该直线上A、B两点离球心的距离.下列说法中正确的是(BC)
A.A点的电势低于B点的电势
B.A点的电场强度方向由A指向B
C.A点的电场强度大于B点的电场强度
D.正电荷沿直线从A移到B的过程中,电场力做负功
【解析】A点的电势高于B点的电势,选项A错误;A点的电场强度方向由A指向B,A点的电场强度大于B点的电场强度,选项B、C正确;正电荷沿直线从A移到B的过程中,电场力做正功,选项D错误.
8.(多选)如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3.0)的切线.现有一质量为0.20 kg,电荷量为+2.0×10-8 C的滑块P(可视作质点),从x=0.10 m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10 m/s2.则下列说法正确的是(CD)
A.滑块运动的加速度逐渐减小
B.滑块运动的速度先减小后增大
C.x=0.15 m处的场强大小为2.0×106 N/C
D.滑块运动的最大速度约为0.10 m/s
【解析】根据E==-,在x轴上的电势φ与坐标x的关系图象斜率的大小表示电场强度,电场强度的方向沿x轴的正方向.由电势φ与坐标x的关系图象可知,沿x轴正方向,电场强度越来越小.滑块从x=0.10 m处由静止释放,所受电场力方向沿x轴正方向,所受电场力越来越小,当电场力等于滑动摩擦力时加速度减小到零.滑块继续运动,做减速运动,加速度增大,所以滑块运动的加速度先减小后增大,选项A错误.滑块先做加速运动,后做减速运动,选项B错误.由E=-,可知x=0.15 m处的场强大小为2.0×106 N/C,选项C正确.当滑动摩擦力等于电场力时,滑块运动的速度最大.滑块所受滑动摩擦力f=μmg=0.04 N.由f=qE可得对应点的电场强度E=2.0×106 N/C,对应的x=0.15 m.由动能定理,qU-μmgΔx=mv2,0.1 m处电势约为4.5×105 V,0.15 m处电势为3.0×105 V,∴U=1.5×105 V,解得v=0.1 m/s.即滑块运动的最大速度约为0.1 m/s,选项D正确.
同课章节目录
