北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第1讲 等腰三角形(基础)含答案
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第1讲 等腰三角形(基础)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-11 17:05:59 | ||
图片预览




文档简介
等腰三角形(基础)知识讲解
【学习目标】
1. 了解等腰三角形、等边三角形的有关概念, 掌握等腰三角形的轴对称性;
2. 掌握等腰三角形、等边三角形的性质,会利用这些性质进行简单的推理、证明、计算和作图.
3. 理解并掌握等腰三角形、等边三角形的判定方法及其证明过程. 通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
4. 理解反证法并能用反证法推理证明简单几何题.
【要点梳理】
要点一、等腰三角形的定义
1.等腰三角形
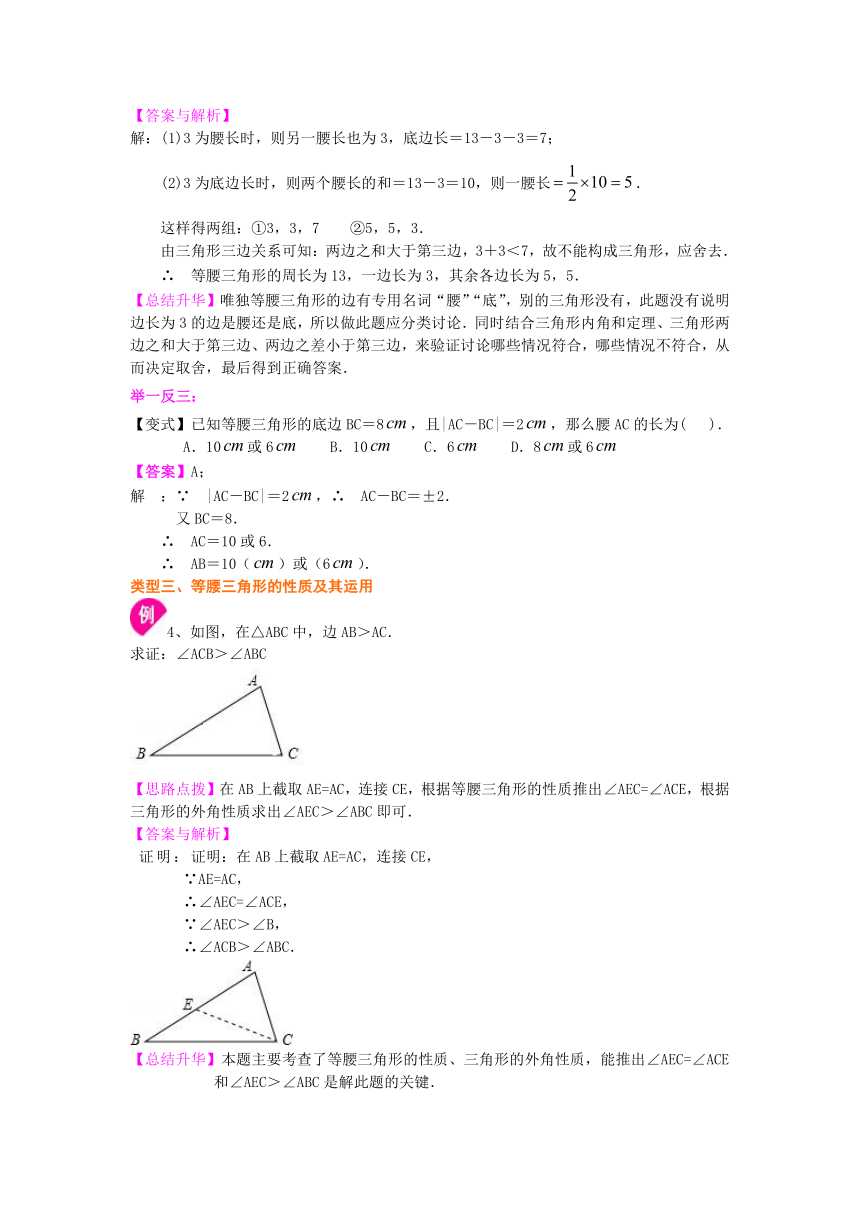
有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,△ABC是等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
2.等腰三角形的作法
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
作法:1.作线段BC=a;
2.分别以B,C为圆心,以b为半径画弧,两弧
相交于点A;
3.连接AB,AC.
△ABC为所求作的等腰三角形
3.等腰三角形的对称性
(1)等腰三角形是轴对称图形;
(2)∠B=∠C;
(3)BD=CD,AD为底边上的中线.
(4)∠ADB=∠ADC=90°,AD为底边上的高线.
结论:等腰三角形是轴对称图形,顶角平分线(底边上的高线或中线)所在的直线是它的对称轴.
4.等边三角形
三条边都相等的三角形叫做等边三角形.也称为正三角形.等边三角形是一类特殊的等腰三角形,有三条对称轴,每个角的平分线(底边上的高线或中线)所在的直线就是它的对称轴.
要点诠释:(1)等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A=180°-2∠B,∠B=∠C= .
(2)等边三角形与等腰三角形的关系:等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
要点二、等腰三角形的性质
1.等腰三角形的性质
性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
推论:等边三角形的三个内角都相等,并且每个内角都等于60°.
性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
2.等腰三角形中重要线段的性质
等腰三角形的两底角的平分线(两腰上的高、两腰上的中线)相等.
要点诠释:这条性质,还可以推广到一下结论:
(1)等腰三角形底边上的高上任一点到两腰的距离相等。
(2)等腰三角形两底边上的中点到两腰的距离相等.
(3)等腰三角形两底角平分线,两腰上的中线,两腰上的高的交点到两腰的距离相等,到底边两端上的距离相等.
(4)等腰三角形顶点到两腰上的高、中线、角平分线的距离相等.
要点三、等腰三角形的判定定理
1.等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
要点诠释:(1)要弄清判定定理的条件和结论,不要与性质定理混淆.判定定理得到的结论是等腰三角形,性质定理是已知三角形是等腰三角形,得到边和角关系.
(2)不能说“一个三角形两底角相等,那么两腰边相等”,因为还未判定它是一个等腰三角形.
2.等边三角形的判定定理
三个角相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
3. 含有30°角的直角三角形
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点四、反证法
在证明时,先假设命题的结论不成立,然后从这个假设出发,经过逐步推导论证,最后推出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果,从而证明命题的结论一定成立,这种证明命题的方法叫做反证法.
要点诠释:反证法也称归谬法,是一种间接证明的方法,一般适用于直接证明有困难的命题.一般证明步骤如下:
(1) 假定命题的结论不成立; (2) 从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果; (3)由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
【典型例题】
类型一、等腰三角形中有关角度的计算题
1、(2019春?太仓市期末)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.
【思路点拨】由于AB=BD=DC,所以△ABD和△BDC都是等腰三角形,可设∠C=∠CDB=x,则∠BDA=∠A=2x,根据等腰三角形的性质和三角形内角和定理的推论,可以求出∠A,∠C度数.
【答案与解析】
解:∵AB=BD,
∴∠BDA=∠A,
∵BD=DC,
∴∠C=∠CBD,
设∠C=∠CBD=x,
则∠BDA=∠A=2x,
∴∠ABD=180°﹣4x,
∴∠ABC=∠ABD+∠CDB=180°﹣4x+x=105°,
解得:x=25°,所以2x=50°,
即∠A=50°,∠C=25°.
【总结升华】本题考查了等腰三角形的性质及三角形内角和定理;解题中运用了等腰三角形“等边对等角”的性质,并联系三角形的内角定理求解有关角的度数问题.
举一反三:
【变式】已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
【答案】
解:∵AC=BC=BD,AD=AE,DE=CE,
∴设∠ECD=∠EDC=,∠BCD=∠BDC=,
则∠AED=∠ADE=2,∠A=∠B=180°-4
在△ABC中,根据三角形内角和得,
++180°-4+180°-4=180°①
又∵A、D、B在同一直线上,∴2++=180°②
由① ,②解得=36°
∴∠B=180°-4=180°-144°=36°.
类型二、等腰三角形中的分类讨论
2、在等腰三角形中,有一个角为40°,求其余各角.
【思路点拨】由一个等腰三角形内角为40°,分别从40°是等腰三角形顶角与40°是底角的角度去分析求解即可求得答案.
【答案与解析】
解:(1)当40°的角为顶角时,由三角形内角和定理可知:
两个底角的度数之和=180°-40°=140°,
又由等腰三角形的性质可知:两底角相等,
故每个底角的度数;
(2)当40°的角为底角时,另一个底角也为40°,
则顶角的度数=180°-40°-40°=100°.
∴其余各角为70°,70°或40°,100°.
【总结升华】此题考查了等腰三角形的性质.此题比较简单,注意掌握分类讨论思想的应用,小心别漏解.
3、已知等腰三角形的周长为13,一边长为3,求其余各边.
【答案与解析】
解:(1)3为腰长时,则另一腰长也为3,底边长=13-3-3=7;
(2)3为底边长时,则两个腰长的和=13-3=10,则一腰长.
这样得两组:①3,3,7 ②5,5,3.
由三角形三边关系可知:两边之和大于第三边,3+3<7,故不能构成三角形,应舍去.
∴ 等腰三角形的周长为13,一边长为3,其余各边长为5,5.
【总结升华】唯独等腰三角形的边有专用名词“腰”“底”,别的三角形没有,此题没有说明边长为3的边是腰还是底,所以做此题应分类讨论.同时结合三角形内角和定理、三角形两边之和大于第三边、两边之差小于第三边,来验证讨论哪些情况符合,哪些情况不符合,从而决定取舍,最后得到正确答案.
举一反三:
【变式】已知等腰三角形的底边BC=8,且|AC-BC|=2,那么腰AC的长为( ).
A.10或6 B.10 C.6 D.8或6
【答案】A;
解 :∵ |AC-BC|=2,∴ AC-BC=±2.
又BC=8.
∴ AC=10或6.
∴ AB=10()或(6).
类型三、等腰三角形的性质及其运用
4、如图,在△ABC中,边AB>AC.
求证:∠ACB>∠ABC
【思路点拨】在AB上截取AE=AC,连接CE,根据等腰三角形的性质推出∠AEC=∠ACE,根据三角形的外角性质求出∠AEC>∠ABC即可.
【答案与解析】
证明:证明:在AB上截取AE=AC,连接CE,
∵AE=AC,
∴∠AEC=∠ACE,
∵∠AEC>∠B,
∴∠ACB>∠ABC.
【总结升华】本题主要考查了等腰三角形的性质、三角形的外角性质,能推出∠AEC=∠ACE和∠AEC>∠ABC是解此题的关键.
举一反三:
【变式】已知:如图,在△ABC中,AB=AC,∠A=60°,BD是中线,延长BC至点E,使CE=CD.
求证:DB=DE.
【答案与解析】
证明:如图,在△ABC中,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠ABC=∠2=60°,
∵BD是中线,
∴BD是∠ABC的平分线,
∴∠1=30°,
∵CE=CD,
∴∠E=∠3,
∴∠E=∠2=30°,
∴∠E=∠1,
∴DB=DE.
类型四、等腰三角形的判定
5、如图1,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作DE∥BC,交AB于点D,交AC于点E.
(1)试找出图中的等腰三角形,并说明理由;
(2)若BD=4、CE=3,求DE的长;
(3)若 AB=12、AC=9,求△ADE的周长;
(4)若将原题中平行线DE的方向改变,如图2,OD∥AB,OE∥AC,BC=16,你能得出什么结论呢?
【思路点拨】(1)运用两三角形两底角相等得出等腰三角形;
(2)由等腰三角形两腰相等求解;
(3)由△ADE的周长=AD+DO+OE+AE=AB+AC求解;
(4)由OD∥AB,OE∥AC,BO平分∠ABC,CO平分∠ACB,得出△BDO和△ECO是等腰三角形,利用等腰三角形两腰相等得出△ODE的周长等于BC的长度.
【答案与解析】
解:(1)△DBO和△EOC是等腰三角形.
∵BO平分∠ABC,
∴∠DBO=∠CBO,
∵DE∥BC,
∴∠CBO=∠DOB,
∴∠DBO=∠DOB,
∴DB=DO,
∴△DBO是等腰三角形,
同理△EOC是等腰三角形;
(2)∵BD=4、CE=3,
∴由(1)得出DO=4,EO=3,
∴DE=DO+OE=4+3=7;
(3)△ADE的周长=AD+DO+OE+AE;
∵DO=DB,OE=EC,
∴△ADE的周长=AB+AC,
∵AB=12、AC=9,
∴△ADE的周长=AB+AC=12+9=21;
(4)∵OD∥AB,OE∥AC,BO平分∠ABC,CO平分∠ACB,
∴△BDO和△ECO是等腰三角形,
∴BD=DO,CE=OE,
∵BC=16,
∴△ODE的周长为16.
即△ODE的周长等于BC的长度.
【总结升华】本题主要考查了等腰三角形的判定与性质及平行线的性质,解题的关键是熟练掌握等腰三角形的两角相等或两边相等.
举一反三
【变式】如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列四个条件:
①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
上述四个条件中,哪两个条件可判定△ABC是等腰三角形,选择其中的一种情形,证明△ABC是等腰三角形.
【答案】①③;②③;①④;②④都可以组合证明△ABC是等腰三角形;选①③为条件证明△ABC是等腰三角形;
证明:∵在△EBO和△DCO中,
∵,
∴△EBO≌△DCO(AAS),
∴BO=CO,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
类型五、 含有30°角的直角三角形
6. 如图所示,△ABC中,∠ACB=90°,CD⊥AB,垂足是D,∠A=60°.求证:BD=3AD.
【答案与解析】证明:∵CD⊥AB,∴∠ADC=90°,
又∵∠A=60°,∴∠ACD=30°
∴在Rt△ACD中,AD=AC,
又∵∠ACB=90°,
在Rt△ACB中,
∴∠B=30°,
∴AC=AB ∴AD= AB,
则AD=BD,即BD=3AD. 【总结升华】根据直角三角形中30°角所对的边是斜边的一半可得到BC=2BD,AB=2BC,从而可推出AB=4BD,从而不难证得BD与AD的数量关系.此题主要考查含30°角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.
举一反三: 【变式】如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
【答案】解:∵AD∥BC,∠A=120°,
∴∠ABC=180°﹣120°=60°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
又∵∠ABC=∠DCB=60°,
∴∠BDC=180°﹣30°﹣60°=90°,
∴BC=2CD=2×4=8cm.
类型六、反证法
7. 求证:在一个三角形中,至少有一个内角小于或等于60°。
【答案】已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°
证明: 假设△ABC中没有一个内角小于或等于60°
则∠A>60°,∠B>60°,∠C>60°∴∠A+∠B+∠C>60°+60°+60°=180°
即∠A+∠B+∠C>180°,这与三角形的内角和为180度矛盾.假设不成立.
∴△ABC中至少有一个内角小于或等于60°
【总结升华】本题结合三角形内角和定理考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是: (1)假设结论不成立; (2)从假设出发推出矛盾; (3)假设的结论不成立,则原题中的结论成立. 在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
举一反三:
【变式】下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A . a= —2 B . a= —1 C . a=1 D. a=2
【答案】A.
【巩固练习】
一.选择题
1. (2019?曲靖一模)等腰三角形中一个外角等于100°,则另两个内角的度数分别为( )
A.40°,40° B.80°,20°
C.50°,50° D.50°,50°或80°,20°
2. 用反证法证明命题:如果AB⊥CD,AB⊥EF,那么CD∥EF,证明的第一个步骤是( )
A. 假设CD∥EF ;
B. 假设AB∥EF
C. 假设CD和EF不平行
D. 假设AB和EF不平行
3. 将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
4. 已知实数x,y满足|x?4|+(y?8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16 B.20 C.16 D.以上答案均不对
5. 如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是( )
A.60° B.70° C.80° D.不确定
6.(2019?永州模拟)在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
7.如图,△ABC中,D为AC边上一点,AD=BD=BC,若∠A=40°,则∠CBD=_____°.
8.(2019?嘉峪关模拟)等腰三角形的两边长分别是2和5,那么它的周长是 .
9.用反证法证明“如果同位角不相等,那么这两条直线不平行“的第一步应假设_________.
10. 等腰三角形的一个角是70°,则它的顶角的度数是 .
11.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是 _________ .(把所有正确答案的序号都填写在横线上)
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
12. 如图,△ABC的周长为32,且AB=AC,AD⊥BC于D,△ACD的周长为24,那么AD的长为 .
三.解答题
13.已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
14.(2019春?安岳县期末)等腰三角形一腰上的中线将三角形的周长分成了21和27两个部分,求等腰三角形的底边和腰长.
15. 用反证法证明:等腰三角形的底角是锐角.
【答案与解析】
一.选择题
1. 【答案】D;
【解析】解:∵外角等于100°,
∴这个内角为80°,
当这个80°角为顶角时,则底角为=50°,此时另两个内角的度数分别为50°,50°;
当这个80°角为底角时,则另一个底角为80°,顶角为20°,此时可得另两个内角的度数分别为80°,20°;
故选D.
2. 【答案】C;
【解析】用反证法证明CD∥EF时,应先假设CD与EF不平行.故选C.
3. 【答案】B;
4. 【答案】B;
【解析】根据题意得 ,
解得
. (1)若4是腰长,则三角形的三边长为:4、4、8, 不能组成三角形; (2)若4是底边长,则三角形的三边长为:4、8、8, 能组成三角形,周长为4+8+8=20. 故选B.
5. 【答案】C;
【解析】AD=DF=BD,∠B=∠BFD=50°,=180°-50°-50°=80°.
6. 【答案】D;
【解析】解:如图,
∵以点O为圆心,以OA为半径画弧,交x轴于点B、C;
以点A为圆心,以AO为半径画弧,交x轴于一点D(点O除外),
∴以OA为腰的等腰三角形有3个;
作OA的垂直平分线,交x轴于一点,
∴以OA为底的等腰三角形有1个,
综上所述,符合条件的点P共有4个,
故选:D.
二.填空题
7. 【答案】20;
【解析】∠A=∠ABD=40°,∠BDC=∠C=80°,所以∠CBD=20°.
8. 【答案】12;
【解析】解:①2是腰长时,三角形的三边分别为2、2、5,
∵2+2=4<5,
∴不能组成三角形,
②2是底边长时,三角形的三边分别为2、5、5,
能组成三角形,
周长=2+5+5=12,
综上所述,它的周长是12.
故答案为:12.
9. 【答案】两直线平行;
【解析】根据已知条件和反证法的特点进行证明,即可求出答案.
10.【答案】70°或40°;
【解析】解:(1)当70°角为顶角,顶角度数即为70°;
(2)当70°为底角时,顶角=180°-2×70°=40°.
故答案为:70°或40°.
11.【答案】②③④;
【解析】:②当∠BAD=∠CAD时,
∵AD是∠BAC的平分线,且AD是BC边上的高;
则△ABD≌△ACD,
∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF;
∵AB+BD=CD+AC,
∴DE=DF,又AD⊥BC;
∴△AEF是等腰三角形;
∴∠E=∠F;
∵AB=BE,
∴∠ABC=2∠E;
同理,得∠ACB=2∠F;
∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;
④△ABC中,AD⊥BC,根据勾股定理,得:
AB2﹣BD2=AC2﹣CD2,
即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD);
∵AB﹣BD=AC﹣CD,
∴AB+BD=AC+CD;
∴两式相加得,
2AB=2AC;
∴AB=AC,
∴△ABC是等腰三角形
故填②③④.
12.【答案】8;
【解析】解:∵AB=AC,AD⊥BC, ∴BD=DC. ∵AB+AC+BC=32, 即AB+BD+CD+AC=32, ∴AC+DC=16 ∴AC+DC+AD=24 ∴AD=8. 故填8.
三.解答题
13.【解析】
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
14.【解析】
解:设等腰三角形的腰长为x,底边长为y,
则有或,
解得:或,
此时两种情况都符合三角形三边关系定理,
答:等腰三角形的腰长为14,底边长为20;或腰长为18,底边长为12.
15.【解析】
证明:假设等腰三角形的底角不是锐角,则它们大于或者等于90°;
根据等腰三角形的两个底角相等,则两个底角的和大于或者等于180°;
则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾;
所以假设错误,原命题正确;
即等腰三角形的底角是锐角.
【学习目标】
1. 了解等腰三角形、等边三角形的有关概念, 掌握等腰三角形的轴对称性;
2. 掌握等腰三角形、等边三角形的性质,会利用这些性质进行简单的推理、证明、计算和作图.
3. 理解并掌握等腰三角形、等边三角形的判定方法及其证明过程. 通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
4. 理解反证法并能用反证法推理证明简单几何题.
【要点梳理】
要点一、等腰三角形的定义
1.等腰三角形
有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,△ABC是等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
2.等腰三角形的作法
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
作法:1.作线段BC=a;
2.分别以B,C为圆心,以b为半径画弧,两弧
相交于点A;
3.连接AB,AC.
△ABC为所求作的等腰三角形
3.等腰三角形的对称性
(1)等腰三角形是轴对称图形;
(2)∠B=∠C;
(3)BD=CD,AD为底边上的中线.
(4)∠ADB=∠ADC=90°,AD为底边上的高线.
结论:等腰三角形是轴对称图形,顶角平分线(底边上的高线或中线)所在的直线是它的对称轴.
4.等边三角形
三条边都相等的三角形叫做等边三角形.也称为正三角形.等边三角形是一类特殊的等腰三角形,有三条对称轴,每个角的平分线(底边上的高线或中线)所在的直线就是它的对称轴.
要点诠释:(1)等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A=180°-2∠B,∠B=∠C= .
(2)等边三角形与等腰三角形的关系:等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
要点二、等腰三角形的性质
1.等腰三角形的性质
性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
推论:等边三角形的三个内角都相等,并且每个内角都等于60°.
性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
2.等腰三角形中重要线段的性质
等腰三角形的两底角的平分线(两腰上的高、两腰上的中线)相等.
要点诠释:这条性质,还可以推广到一下结论:
(1)等腰三角形底边上的高上任一点到两腰的距离相等。
(2)等腰三角形两底边上的中点到两腰的距离相等.
(3)等腰三角形两底角平分线,两腰上的中线,两腰上的高的交点到两腰的距离相等,到底边两端上的距离相等.
(4)等腰三角形顶点到两腰上的高、中线、角平分线的距离相等.
要点三、等腰三角形的判定定理
1.等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
要点诠释:(1)要弄清判定定理的条件和结论,不要与性质定理混淆.判定定理得到的结论是等腰三角形,性质定理是已知三角形是等腰三角形,得到边和角关系.
(2)不能说“一个三角形两底角相等,那么两腰边相等”,因为还未判定它是一个等腰三角形.
2.等边三角形的判定定理
三个角相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
3. 含有30°角的直角三角形
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点四、反证法
在证明时,先假设命题的结论不成立,然后从这个假设出发,经过逐步推导论证,最后推出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果,从而证明命题的结论一定成立,这种证明命题的方法叫做反证法.
要点诠释:反证法也称归谬法,是一种间接证明的方法,一般适用于直接证明有困难的命题.一般证明步骤如下:
(1) 假定命题的结论不成立; (2) 从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果; (3)由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
【典型例题】
类型一、等腰三角形中有关角度的计算题
1、(2019春?太仓市期末)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.
【思路点拨】由于AB=BD=DC,所以△ABD和△BDC都是等腰三角形,可设∠C=∠CDB=x,则∠BDA=∠A=2x,根据等腰三角形的性质和三角形内角和定理的推论,可以求出∠A,∠C度数.
【答案与解析】
解:∵AB=BD,
∴∠BDA=∠A,
∵BD=DC,
∴∠C=∠CBD,
设∠C=∠CBD=x,
则∠BDA=∠A=2x,
∴∠ABD=180°﹣4x,
∴∠ABC=∠ABD+∠CDB=180°﹣4x+x=105°,
解得:x=25°,所以2x=50°,
即∠A=50°,∠C=25°.
【总结升华】本题考查了等腰三角形的性质及三角形内角和定理;解题中运用了等腰三角形“等边对等角”的性质,并联系三角形的内角定理求解有关角的度数问题.
举一反三:
【变式】已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
【答案】
解:∵AC=BC=BD,AD=AE,DE=CE,
∴设∠ECD=∠EDC=,∠BCD=∠BDC=,
则∠AED=∠ADE=2,∠A=∠B=180°-4
在△ABC中,根据三角形内角和得,
++180°-4+180°-4=180°①
又∵A、D、B在同一直线上,∴2++=180°②
由① ,②解得=36°
∴∠B=180°-4=180°-144°=36°.
类型二、等腰三角形中的分类讨论
2、在等腰三角形中,有一个角为40°,求其余各角.
【思路点拨】由一个等腰三角形内角为40°,分别从40°是等腰三角形顶角与40°是底角的角度去分析求解即可求得答案.
【答案与解析】
解:(1)当40°的角为顶角时,由三角形内角和定理可知:
两个底角的度数之和=180°-40°=140°,
又由等腰三角形的性质可知:两底角相等,
故每个底角的度数;
(2)当40°的角为底角时,另一个底角也为40°,
则顶角的度数=180°-40°-40°=100°.
∴其余各角为70°,70°或40°,100°.
【总结升华】此题考查了等腰三角形的性质.此题比较简单,注意掌握分类讨论思想的应用,小心别漏解.
3、已知等腰三角形的周长为13,一边长为3,求其余各边.
【答案与解析】
解:(1)3为腰长时,则另一腰长也为3,底边长=13-3-3=7;
(2)3为底边长时,则两个腰长的和=13-3=10,则一腰长.
这样得两组:①3,3,7 ②5,5,3.
由三角形三边关系可知:两边之和大于第三边,3+3<7,故不能构成三角形,应舍去.
∴ 等腰三角形的周长为13,一边长为3,其余各边长为5,5.
【总结升华】唯独等腰三角形的边有专用名词“腰”“底”,别的三角形没有,此题没有说明边长为3的边是腰还是底,所以做此题应分类讨论.同时结合三角形内角和定理、三角形两边之和大于第三边、两边之差小于第三边,来验证讨论哪些情况符合,哪些情况不符合,从而决定取舍,最后得到正确答案.
举一反三:
【变式】已知等腰三角形的底边BC=8,且|AC-BC|=2,那么腰AC的长为( ).
A.10或6 B.10 C.6 D.8或6
【答案】A;
解 :∵ |AC-BC|=2,∴ AC-BC=±2.
又BC=8.
∴ AC=10或6.
∴ AB=10()或(6).
类型三、等腰三角形的性质及其运用
4、如图,在△ABC中,边AB>AC.
求证:∠ACB>∠ABC
【思路点拨】在AB上截取AE=AC,连接CE,根据等腰三角形的性质推出∠AEC=∠ACE,根据三角形的外角性质求出∠AEC>∠ABC即可.
【答案与解析】
证明:证明:在AB上截取AE=AC,连接CE,
∵AE=AC,
∴∠AEC=∠ACE,
∵∠AEC>∠B,
∴∠ACB>∠ABC.
【总结升华】本题主要考查了等腰三角形的性质、三角形的外角性质,能推出∠AEC=∠ACE和∠AEC>∠ABC是解此题的关键.
举一反三:
【变式】已知:如图,在△ABC中,AB=AC,∠A=60°,BD是中线,延长BC至点E,使CE=CD.
求证:DB=DE.
【答案与解析】
证明:如图,在△ABC中,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠ABC=∠2=60°,
∵BD是中线,
∴BD是∠ABC的平分线,
∴∠1=30°,
∵CE=CD,
∴∠E=∠3,
∴∠E=∠2=30°,
∴∠E=∠1,
∴DB=DE.
类型四、等腰三角形的判定
5、如图1,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作DE∥BC,交AB于点D,交AC于点E.
(1)试找出图中的等腰三角形,并说明理由;
(2)若BD=4、CE=3,求DE的长;
(3)若 AB=12、AC=9,求△ADE的周长;
(4)若将原题中平行线DE的方向改变,如图2,OD∥AB,OE∥AC,BC=16,你能得出什么结论呢?
【思路点拨】(1)运用两三角形两底角相等得出等腰三角形;
(2)由等腰三角形两腰相等求解;
(3)由△ADE的周长=AD+DO+OE+AE=AB+AC求解;
(4)由OD∥AB,OE∥AC,BO平分∠ABC,CO平分∠ACB,得出△BDO和△ECO是等腰三角形,利用等腰三角形两腰相等得出△ODE的周长等于BC的长度.
【答案与解析】
解:(1)△DBO和△EOC是等腰三角形.
∵BO平分∠ABC,
∴∠DBO=∠CBO,
∵DE∥BC,
∴∠CBO=∠DOB,
∴∠DBO=∠DOB,
∴DB=DO,
∴△DBO是等腰三角形,
同理△EOC是等腰三角形;
(2)∵BD=4、CE=3,
∴由(1)得出DO=4,EO=3,
∴DE=DO+OE=4+3=7;
(3)△ADE的周长=AD+DO+OE+AE;
∵DO=DB,OE=EC,
∴△ADE的周长=AB+AC,
∵AB=12、AC=9,
∴△ADE的周长=AB+AC=12+9=21;
(4)∵OD∥AB,OE∥AC,BO平分∠ABC,CO平分∠ACB,
∴△BDO和△ECO是等腰三角形,
∴BD=DO,CE=OE,
∵BC=16,
∴△ODE的周长为16.
即△ODE的周长等于BC的长度.
【总结升华】本题主要考查了等腰三角形的判定与性质及平行线的性质,解题的关键是熟练掌握等腰三角形的两角相等或两边相等.
举一反三
【变式】如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列四个条件:
①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
上述四个条件中,哪两个条件可判定△ABC是等腰三角形,选择其中的一种情形,证明△ABC是等腰三角形.
【答案】①③;②③;①④;②④都可以组合证明△ABC是等腰三角形;选①③为条件证明△ABC是等腰三角形;
证明:∵在△EBO和△DCO中,
∵,
∴△EBO≌△DCO(AAS),
∴BO=CO,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
类型五、 含有30°角的直角三角形
6. 如图所示,△ABC中,∠ACB=90°,CD⊥AB,垂足是D,∠A=60°.求证:BD=3AD.
【答案与解析】证明:∵CD⊥AB,∴∠ADC=90°,
又∵∠A=60°,∴∠ACD=30°
∴在Rt△ACD中,AD=AC,
又∵∠ACB=90°,
在Rt△ACB中,
∴∠B=30°,
∴AC=AB ∴AD= AB,
则AD=BD,即BD=3AD. 【总结升华】根据直角三角形中30°角所对的边是斜边的一半可得到BC=2BD,AB=2BC,从而可推出AB=4BD,从而不难证得BD与AD的数量关系.此题主要考查含30°角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.
举一反三: 【变式】如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
【答案】解:∵AD∥BC,∠A=120°,
∴∠ABC=180°﹣120°=60°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
又∵∠ABC=∠DCB=60°,
∴∠BDC=180°﹣30°﹣60°=90°,
∴BC=2CD=2×4=8cm.
类型六、反证法
7. 求证:在一个三角形中,至少有一个内角小于或等于60°。
【答案】已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°
证明: 假设△ABC中没有一个内角小于或等于60°
则∠A>60°,∠B>60°,∠C>60°∴∠A+∠B+∠C>60°+60°+60°=180°
即∠A+∠B+∠C>180°,这与三角形的内角和为180度矛盾.假设不成立.
∴△ABC中至少有一个内角小于或等于60°
【总结升华】本题结合三角形内角和定理考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是: (1)假设结论不成立; (2)从假设出发推出矛盾; (3)假设的结论不成立,则原题中的结论成立. 在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
举一反三:
【变式】下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A . a= —2 B . a= —1 C . a=1 D. a=2
【答案】A.
【巩固练习】
一.选择题
1. (2019?曲靖一模)等腰三角形中一个外角等于100°,则另两个内角的度数分别为( )
A.40°,40° B.80°,20°
C.50°,50° D.50°,50°或80°,20°
2. 用反证法证明命题:如果AB⊥CD,AB⊥EF,那么CD∥EF,证明的第一个步骤是( )
A. 假设CD∥EF ;
B. 假设AB∥EF
C. 假设CD和EF不平行
D. 假设AB和EF不平行
3. 将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
4. 已知实数x,y满足|x?4|+(y?8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16 B.20 C.16 D.以上答案均不对
5. 如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是( )
A.60° B.70° C.80° D.不确定
6.(2019?永州模拟)在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
7.如图,△ABC中,D为AC边上一点,AD=BD=BC,若∠A=40°,则∠CBD=_____°.
8.(2019?嘉峪关模拟)等腰三角形的两边长分别是2和5,那么它的周长是 .
9.用反证法证明“如果同位角不相等,那么这两条直线不平行“的第一步应假设_________.
10. 等腰三角形的一个角是70°,则它的顶角的度数是 .
11.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是 _________ .(把所有正确答案的序号都填写在横线上)
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
12. 如图,△ABC的周长为32,且AB=AC,AD⊥BC于D,△ACD的周长为24,那么AD的长为 .
三.解答题
13.已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
14.(2019春?安岳县期末)等腰三角形一腰上的中线将三角形的周长分成了21和27两个部分,求等腰三角形的底边和腰长.
15. 用反证法证明:等腰三角形的底角是锐角.
【答案与解析】
一.选择题
1. 【答案】D;
【解析】解:∵外角等于100°,
∴这个内角为80°,
当这个80°角为顶角时,则底角为=50°,此时另两个内角的度数分别为50°,50°;
当这个80°角为底角时,则另一个底角为80°,顶角为20°,此时可得另两个内角的度数分别为80°,20°;
故选D.
2. 【答案】C;
【解析】用反证法证明CD∥EF时,应先假设CD与EF不平行.故选C.
3. 【答案】B;
4. 【答案】B;
【解析】根据题意得 ,
解得
. (1)若4是腰长,则三角形的三边长为:4、4、8, 不能组成三角形; (2)若4是底边长,则三角形的三边长为:4、8、8, 能组成三角形,周长为4+8+8=20. 故选B.
5. 【答案】C;
【解析】AD=DF=BD,∠B=∠BFD=50°,=180°-50°-50°=80°.
6. 【答案】D;
【解析】解:如图,
∵以点O为圆心,以OA为半径画弧,交x轴于点B、C;
以点A为圆心,以AO为半径画弧,交x轴于一点D(点O除外),
∴以OA为腰的等腰三角形有3个;
作OA的垂直平分线,交x轴于一点,
∴以OA为底的等腰三角形有1个,
综上所述,符合条件的点P共有4个,
故选:D.
二.填空题
7. 【答案】20;
【解析】∠A=∠ABD=40°,∠BDC=∠C=80°,所以∠CBD=20°.
8. 【答案】12;
【解析】解:①2是腰长时,三角形的三边分别为2、2、5,
∵2+2=4<5,
∴不能组成三角形,
②2是底边长时,三角形的三边分别为2、5、5,
能组成三角形,
周长=2+5+5=12,
综上所述,它的周长是12.
故答案为:12.
9. 【答案】两直线平行;
【解析】根据已知条件和反证法的特点进行证明,即可求出答案.
10.【答案】70°或40°;
【解析】解:(1)当70°角为顶角,顶角度数即为70°;
(2)当70°为底角时,顶角=180°-2×70°=40°.
故答案为:70°或40°.
11.【答案】②③④;
【解析】:②当∠BAD=∠CAD时,
∵AD是∠BAC的平分线,且AD是BC边上的高;
则△ABD≌△ACD,
∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF;
∵AB+BD=CD+AC,
∴DE=DF,又AD⊥BC;
∴△AEF是等腰三角形;
∴∠E=∠F;
∵AB=BE,
∴∠ABC=2∠E;
同理,得∠ACB=2∠F;
∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;
④△ABC中,AD⊥BC,根据勾股定理,得:
AB2﹣BD2=AC2﹣CD2,
即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD);
∵AB﹣BD=AC﹣CD,
∴AB+BD=AC+CD;
∴两式相加得,
2AB=2AC;
∴AB=AC,
∴△ABC是等腰三角形
故填②③④.
12.【答案】8;
【解析】解:∵AB=AC,AD⊥BC, ∴BD=DC. ∵AB+AC+BC=32, 即AB+BD+CD+AC=32, ∴AC+DC=16 ∴AC+DC+AD=24 ∴AD=8. 故填8.
三.解答题
13.【解析】
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
14.【解析】
解:设等腰三角形的腰长为x,底边长为y,
则有或,
解得:或,
此时两种情况都符合三角形三边关系定理,
答:等腰三角形的腰长为14,底边长为20;或腰长为18,底边长为12.
15.【解析】
证明:假设等腰三角形的底角不是锐角,则它们大于或者等于90°;
根据等腰三角形的两个底角相等,则两个底角的和大于或者等于180°;
则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾;
所以假设错误,原命题正确;
即等腰三角形的底角是锐角.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
