北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第9讲 一次函数与一元一次不等式(基础)
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第9讲 一次函数与一元一次不等式(基础) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-11 00:00:00 | ||
图片预览


文档简介
一次函数与一元一次不等式(基础)
【学习目标】
1.能用函数的观点认识一次函数、一次方程(组)与一元一次不等式之间的联系,能直观地用图形(在平面直角坐标系中)来表示方程(或方程组)的解及不等式的解,建立数形结合的思想及转化的思想.
2.能运用一次函数的性质解决简单的不等式问题及实际问题.
【要点梳理】
要点一、一次函数与一元一次不等式
由于任何一个一元一次不等式都可以转化为>0或<0或≥0或≤0(、为常数,≠0)的形式,所以解一元一次不等式可以看作:当一次函数的值大于0(或小于0或大于等于0或小于等于0)时求相应的自变量的取值范围.
要点诠释:求关于的一元一次不等式>0(≠0)的解集,从“数”的角度看,就是为何值时,函数的值大于0?从“形”的角度看,确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围.
要点二、一元一次方程与一元一次不等式
我们已经学过,利用不等式的性质可以解得一个一元一次不等式的解集,这个不等式的解集的端点值就是我们把不等式中的不等号变为等号时对应方程的解.
要点三、如何确定两个不等式的大小关系
(≠,且)的解集的函数值大于的函数值时的自变量取值范围直线在直线的上方对应的点的横坐标范围.
【典型例题】
类型一、一次函数与一元一次不等式
1、如图,直线交坐标轴于A(-3,0)、B(0,5)两点,则不等式<0的解集为( )
A.>-3 B.<-3 C.>3 D.<3
【思路点拨】<0即>0,图象在轴上方所有点的横坐标的集合就构成不等式>0的解集.
【答案】A;
【解析】观察图象可知,当>-3时,直线落在轴的上方,
即不等式>0的解集为>-3,
∵<0
∴>0,
∴<0解集为>-3.
【总结升华】本题考查了一次函数与不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.
举一反三:
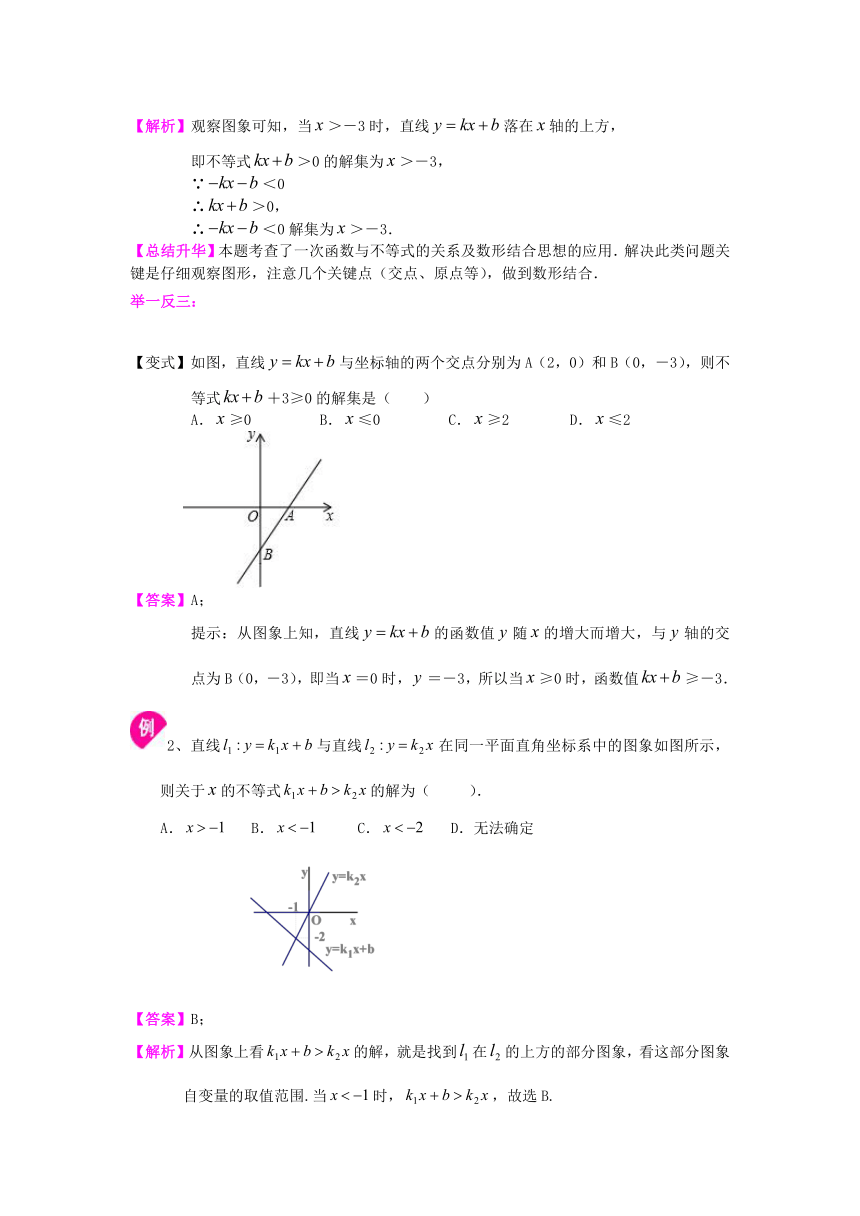
【变式】如图,直线与坐标轴的两个交点分别为A(2,0)和B(0,-3),则不等式+3≥0的解集是( )
A.≥0 B.≤0 C.≥2 D.≤2
【答案】A;
提示:从图象上知,直线的函数值随的增大而增大,与轴的交点为B(0,-3),即当=0时,=-3,所以当≥0时,函数值≥-3.
2、直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为( ).
A. B. C. D.无法确定
【答案】B;
【解析】从图象上看的解,就是找到在的上方的部分图象,看这部分图象自变量的取值范围.当时,,故选B.
【总结升华】本题考察了用数形结合的方法求解不等式的大小关系,解题的关键是找出表示两条直线的交点的横坐标,再根据在上方的图象表示的函数值大,下方的图象表示的函数值小来解题.
举一反三:
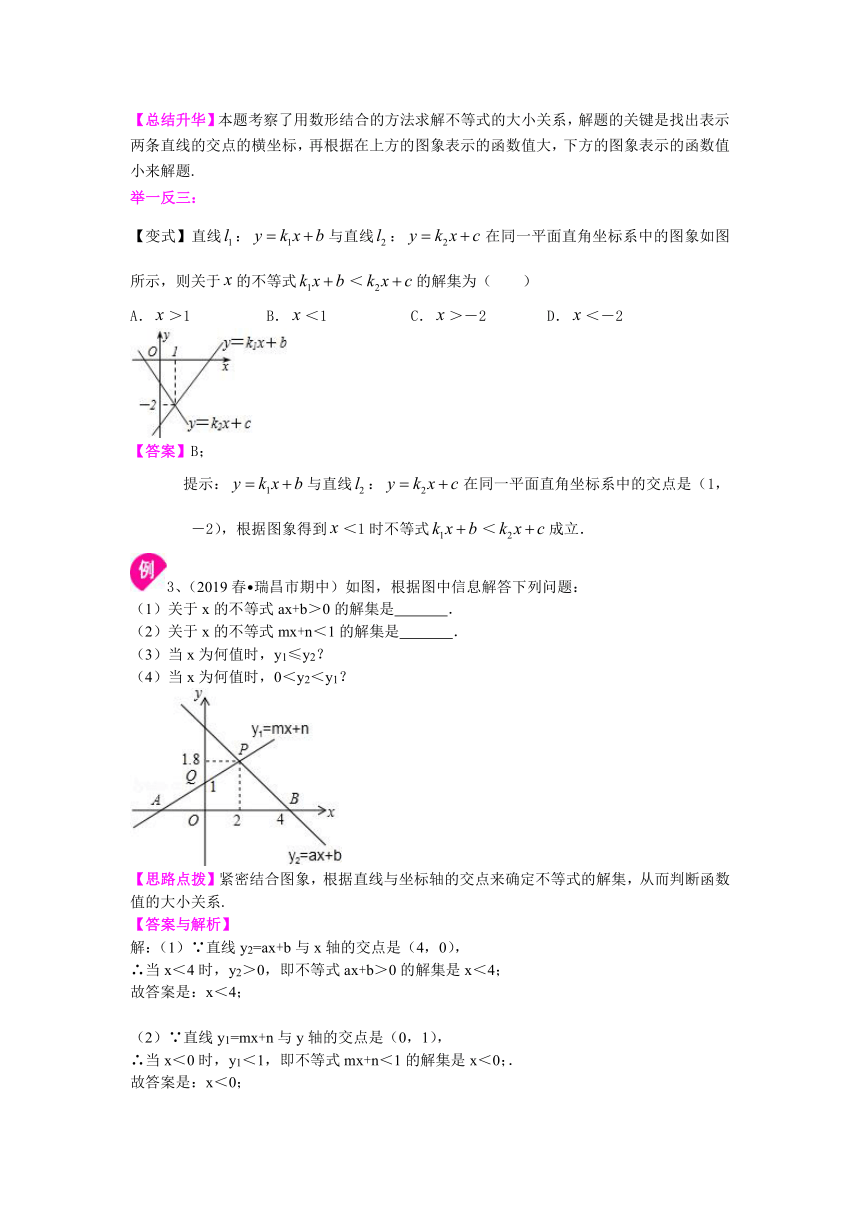
【变式】直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于的不等式<的解集为( )
A.>1 B.<1 C.>-2 D.<-2
【答案】B;
提示:与直线:在同一平面直角坐标系中的交点是(1,-2),根据图象得到<1时不等式<成立.
3、(2019春?瑞昌市期中)如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
【思路点拨】紧密结合图象,根据直线与坐标轴的交点来确定不等式的解集,从而判断函数值的大小关系.
【答案与解析】
解:(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4;
故答案是:x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0;.
故答案是:x<0;
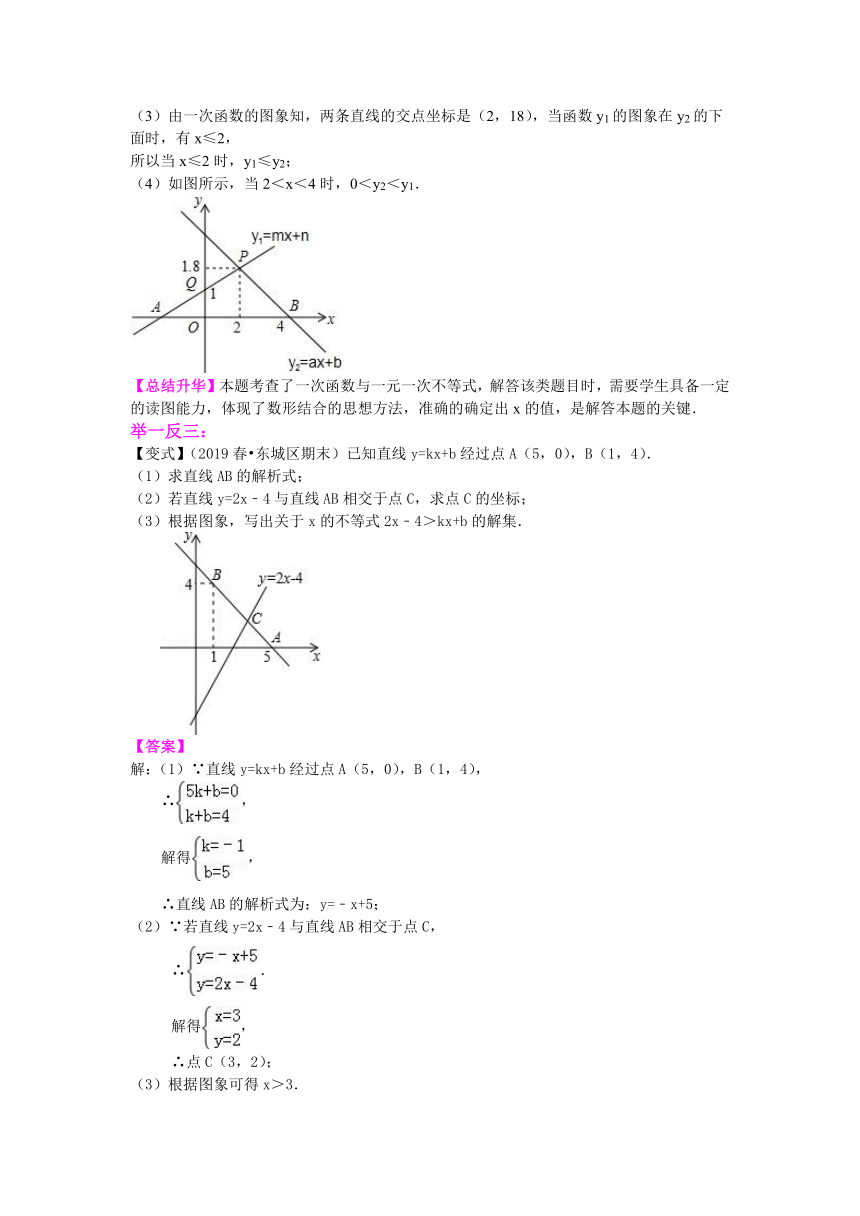
(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,
所以当x≤2时,y1≤y2;
(4)如图所示,当2<x<4时,0<y2<y1.
【总结升华】本题考查了一次函数与一元一次不等式,解答该类题目时,需要学生具备一定的读图能力,体现了数形结合的思想方法,准确的确定出x的值,是解答本题的关键.
举一反三:
【变式】(2019春?东城区期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
【答案】
解:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴,
解得,
∴直线AB的解析式为:y=﹣x+5;
(2)∵若直线y=2x﹣4与直线AB相交于点C,
∴.
解得,
∴点C(3,2);
(3)根据图象可得x>3.
类型二、用一次函数的性质解决不等式的实际问题
4、(2019?新疆)某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
品牌
进价/(元/件)
售价/(元/件)
A
50
80
B
40
65
(1)求W关于x的函数关系式;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价﹣进价)
【思路点拨】(1)由总利润=A品牌T恤的利润+B品牌T恤的利润就可以求出w关于x的函数关系式;
(2)根据“两种T恤的总费用不超过9500元”建立不等式求出x的取值范围,由一次函数性质就可以求出结论.
【答案与解析】
解:(1)设购进A种T恤x件,则购进B种T恤(200﹣x)件,由题意得:
w=(80﹣50)x+(65﹣40)(200﹣x),
w=30x+5000﹣25x,
w=5x+5000.
答:w关于x的函数关系式为w=5x+5000;
(2)∵购进两种T恤的总费用不超过9500元,
∴50x+40(200﹣x)≤9500,
∴x≤150.
∵w=5x+5000.
∴k=5>0
∴w随x的增大而增大,
∴x=150时,w的最大值为5750.
∴购进A种T恤150件.
∴购进A种T恤150件,购进B种T恤50件可获得最大利润,最大利润为5750元.
【总结升华】本题考查了由销售问题的数量关系求函数的解析式的运用,列一元一次不等式解实际问题的运用,一次函数的性质的运用,解答时求出函数的解析式是关键.
【巩固练习】
一.选择题
1. (2019春?武侯区期末)如图,直线y=kx+b与坐标轴的两交点分别为A(2,0)和B(0,﹣3),则不等式kx+b+3≤0的解为( )
A.x≤0 B.x≥0 C.x≥2 D.x≤2
2.(2019?富顺县校级二模)一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
A.y>0 B.﹣2<y≤0 C.﹣2<y≤1 D.无法判断
3. 已知关于的不等式>0(≠0)的解集是<1,则直线与轴的交点是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
4. 如图,已知函数和的图象交于点P(-2,-5),则根据图象可得不等式>的解集在数轴上表示正确的是( )
A. B. C. D.
5. 如图,反映了某公司的销售收入与销售量的关系,反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量( )
A.小于3吨 B.大于3吨 C.小于4吨 D.大于4吨
6. 如图,已知函数和的图象交于点P(-2,-5),则下列结论正确的是( )
A.<-2时,< B.<-2时,>
C.<0 D.<0
二.填空题
7. 不等式2-6<+6的解集,表示对于同一个的值,函数的图象上的点在的图象上的点的_______方.
8. 已知直线和的图象如图所示,根据图象填空.当______时,=;当_______时,<;方程组的解是______.
9. 一次函数与的图象如图,则下列结论①;②;③当时,中,正确的是______.
10. 一次函数与的图象如图所示,则当______时,<;当______时,=;当______时,>.
11.(2019春?冠县校级期末)如图,直线y=kx+b经过A(﹣1,1)和B(﹣,0)两点,则不等式组0<kx+b<1的解集为 .
12. 已知不等式>的解集是<2,则直线与的交点坐标是_______.
三.解答题
13. 在同一直角坐标系中 (1)作出函数和的图象.
(2)用图象法求不等式>的解集.
14.(2019秋?岳阳校级期中)某移动通信公司开展两种业务:“全球通”使用者缴30元月租费,然后每通话一分钟再付费0.25元;“神州行”不缴月租费,每通话一分钟付话费0.40元.若一个月内通话x分钟.
(1)用代数式表示两种方式的费用各是多少?
(2)若某人估计一个月内通话200分钟,应选择哪一种方式合算些?
15.(2019?曲靖)如图,已知直线y1=﹣x+1与x轴交于点A,与直线y2=﹣x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】解:由kx+b+3≤0得kx+b≤﹣3,
直线y=kx+b与y轴的交点为B(0,﹣3),
即当x=0时,y=﹣3,
由图象可看出,不等式kx+b+3≤0的解集是x≤0.
故选A.
2. 【答案】B;
【解析】因为一次函数y=kx+b的图象与两坐标轴的交点分别为(1,0)、(0,﹣2),
所以当0<x≤1,函数y的取值范围是:﹣2<y≤0,故选B.
3. 【答案】D;
【解析】由于关于的不等式>0(≠0)的解集是<1,即当=1时,函数的值为0,故可得到直线与轴的交点坐标.
4. 【答案】C;
【解析】从图象得到,当>-2时,的图象对应的点在函数的图象上面,∴不等式>的解集为>-2.
5. 【答案】D;
【解析】当>4时,>.
6. 【答案】A;
【解析】A、由图象可知<-2时,<,故正确;B、由图象可知<-2时, <,故错误;C、由经过一、三象限是<0,经过四象限是>0,故错误;D、由函数一、二、三象限,可知>0,故错误.
二.填空题
7. 【答案】下;
8. 【答案】=0;<0;;
9. 【答案】① ;
【解析】由图象可知,<0,<0,当时,的图象在的上方,所以,所以只有①正确.
10.【答案】>1;=1;<1;
11.【答案】﹣<x<1;
【解析】解:由题意可得:一次函数图象在y=1的下方时x<﹣1,在y=0的上方时x>﹣,∴关于x的不等式0<kx+b<1的解集是﹣<x<﹣1.
12.【答案】(2,3);
【解析】已知不等式>的解集是<2,则当=2时,-+5=3-3;即当=2时,函数与的函数值相等;因而直线与的交点坐标是:(2,3).
三.解答题
13.【解析】
解:(1)对于,当=0时,=2;当=0时,=2, 即过点(0,2)和点(2,0),过这两点作直线即为的图象; 对于,当=0时,=-4;当=0时,=2, 即过点(0,-4)和点(2,0),过这两点作直线即为的图象. 图象如下图:
(2)从图象得出,当<2时,函数的图象在函数的上方, ∴不等式>的解集为:<2.
14.【解析】
解:(1)设两种费用分别为:y1,y2,
依题意可得:y1=30+0.25x,y2=0.4x;
(2)当x=200时,y1=80,y2=80,两种方式一样.
15.【解析】
解:(1)由y1=﹣x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2,
∵y1=﹣x+1与直线y2=﹣x交于点B,
∴B点的坐标是(﹣1,1.5),
∴△AOB的面积=×2×1.5=1.5;
(2)由(1)可知交点B的坐标是(﹣1,1.5),
由函数图象可知y1>y2时,x>﹣1.
【学习目标】
1.能用函数的观点认识一次函数、一次方程(组)与一元一次不等式之间的联系,能直观地用图形(在平面直角坐标系中)来表示方程(或方程组)的解及不等式的解,建立数形结合的思想及转化的思想.
2.能运用一次函数的性质解决简单的不等式问题及实际问题.
【要点梳理】
要点一、一次函数与一元一次不等式
由于任何一个一元一次不等式都可以转化为>0或<0或≥0或≤0(、为常数,≠0)的形式,所以解一元一次不等式可以看作:当一次函数的值大于0(或小于0或大于等于0或小于等于0)时求相应的自变量的取值范围.
要点诠释:求关于的一元一次不等式>0(≠0)的解集,从“数”的角度看,就是为何值时,函数的值大于0?从“形”的角度看,确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围.
要点二、一元一次方程与一元一次不等式
我们已经学过,利用不等式的性质可以解得一个一元一次不等式的解集,这个不等式的解集的端点值就是我们把不等式中的不等号变为等号时对应方程的解.
要点三、如何确定两个不等式的大小关系
(≠,且)的解集的函数值大于的函数值时的自变量取值范围直线在直线的上方对应的点的横坐标范围.
【典型例题】
类型一、一次函数与一元一次不等式
1、如图,直线交坐标轴于A(-3,0)、B(0,5)两点,则不等式<0的解集为( )
A.>-3 B.<-3 C.>3 D.<3
【思路点拨】<0即>0,图象在轴上方所有点的横坐标的集合就构成不等式>0的解集.
【答案】A;
【解析】观察图象可知,当>-3时,直线落在轴的上方,
即不等式>0的解集为>-3,
∵<0
∴>0,
∴<0解集为>-3.
【总结升华】本题考查了一次函数与不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.
举一反三:
【变式】如图,直线与坐标轴的两个交点分别为A(2,0)和B(0,-3),则不等式+3≥0的解集是( )
A.≥0 B.≤0 C.≥2 D.≤2
【答案】A;
提示:从图象上知,直线的函数值随的增大而增大,与轴的交点为B(0,-3),即当=0时,=-3,所以当≥0时,函数值≥-3.
2、直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为( ).
A. B. C. D.无法确定
【答案】B;
【解析】从图象上看的解,就是找到在的上方的部分图象,看这部分图象自变量的取值范围.当时,,故选B.
【总结升华】本题考察了用数形结合的方法求解不等式的大小关系,解题的关键是找出表示两条直线的交点的横坐标,再根据在上方的图象表示的函数值大,下方的图象表示的函数值小来解题.
举一反三:
【变式】直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于的不等式<的解集为( )
A.>1 B.<1 C.>-2 D.<-2
【答案】B;
提示:与直线:在同一平面直角坐标系中的交点是(1,-2),根据图象得到<1时不等式<成立.
3、(2019春?瑞昌市期中)如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
【思路点拨】紧密结合图象,根据直线与坐标轴的交点来确定不等式的解集,从而判断函数值的大小关系.
【答案与解析】
解:(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4;
故答案是:x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0;.
故答案是:x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,
所以当x≤2时,y1≤y2;
(4)如图所示,当2<x<4时,0<y2<y1.
【总结升华】本题考查了一次函数与一元一次不等式,解答该类题目时,需要学生具备一定的读图能力,体现了数形结合的思想方法,准确的确定出x的值,是解答本题的关键.
举一反三:
【变式】(2019春?东城区期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
【答案】
解:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴,
解得,
∴直线AB的解析式为:y=﹣x+5;
(2)∵若直线y=2x﹣4与直线AB相交于点C,
∴.
解得,
∴点C(3,2);
(3)根据图象可得x>3.
类型二、用一次函数的性质解决不等式的实际问题
4、(2019?新疆)某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
品牌
进价/(元/件)
售价/(元/件)
A
50
80
B
40
65
(1)求W关于x的函数关系式;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价﹣进价)
【思路点拨】(1)由总利润=A品牌T恤的利润+B品牌T恤的利润就可以求出w关于x的函数关系式;
(2)根据“两种T恤的总费用不超过9500元”建立不等式求出x的取值范围,由一次函数性质就可以求出结论.
【答案与解析】
解:(1)设购进A种T恤x件,则购进B种T恤(200﹣x)件,由题意得:
w=(80﹣50)x+(65﹣40)(200﹣x),
w=30x+5000﹣25x,
w=5x+5000.
答:w关于x的函数关系式为w=5x+5000;
(2)∵购进两种T恤的总费用不超过9500元,
∴50x+40(200﹣x)≤9500,
∴x≤150.
∵w=5x+5000.
∴k=5>0
∴w随x的增大而增大,
∴x=150时,w的最大值为5750.
∴购进A种T恤150件.
∴购进A种T恤150件,购进B种T恤50件可获得最大利润,最大利润为5750元.
【总结升华】本题考查了由销售问题的数量关系求函数的解析式的运用,列一元一次不等式解实际问题的运用,一次函数的性质的运用,解答时求出函数的解析式是关键.
【巩固练习】
一.选择题
1. (2019春?武侯区期末)如图,直线y=kx+b与坐标轴的两交点分别为A(2,0)和B(0,﹣3),则不等式kx+b+3≤0的解为( )
A.x≤0 B.x≥0 C.x≥2 D.x≤2
2.(2019?富顺县校级二模)一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
A.y>0 B.﹣2<y≤0 C.﹣2<y≤1 D.无法判断
3. 已知关于的不等式>0(≠0)的解集是<1,则直线与轴的交点是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
4. 如图,已知函数和的图象交于点P(-2,-5),则根据图象可得不等式>的解集在数轴上表示正确的是( )
A. B. C. D.
5. 如图,反映了某公司的销售收入与销售量的关系,反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量( )
A.小于3吨 B.大于3吨 C.小于4吨 D.大于4吨
6. 如图,已知函数和的图象交于点P(-2,-5),则下列结论正确的是( )
A.<-2时,< B.<-2时,>
C.<0 D.<0
二.填空题
7. 不等式2-6<+6的解集,表示对于同一个的值,函数的图象上的点在的图象上的点的_______方.
8. 已知直线和的图象如图所示,根据图象填空.当______时,=;当_______时,<;方程组的解是______.
9. 一次函数与的图象如图,则下列结论①;②;③当时,中,正确的是______.
10. 一次函数与的图象如图所示,则当______时,<;当______时,=;当______时,>.
11.(2019春?冠县校级期末)如图,直线y=kx+b经过A(﹣1,1)和B(﹣,0)两点,则不等式组0<kx+b<1的解集为 .
12. 已知不等式>的解集是<2,则直线与的交点坐标是_______.
三.解答题
13. 在同一直角坐标系中 (1)作出函数和的图象.
(2)用图象法求不等式>的解集.
14.(2019秋?岳阳校级期中)某移动通信公司开展两种业务:“全球通”使用者缴30元月租费,然后每通话一分钟再付费0.25元;“神州行”不缴月租费,每通话一分钟付话费0.40元.若一个月内通话x分钟.
(1)用代数式表示两种方式的费用各是多少?
(2)若某人估计一个月内通话200分钟,应选择哪一种方式合算些?
15.(2019?曲靖)如图,已知直线y1=﹣x+1与x轴交于点A,与直线y2=﹣x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】解:由kx+b+3≤0得kx+b≤﹣3,
直线y=kx+b与y轴的交点为B(0,﹣3),
即当x=0时,y=﹣3,
由图象可看出,不等式kx+b+3≤0的解集是x≤0.
故选A.
2. 【答案】B;
【解析】因为一次函数y=kx+b的图象与两坐标轴的交点分别为(1,0)、(0,﹣2),
所以当0<x≤1,函数y的取值范围是:﹣2<y≤0,故选B.
3. 【答案】D;
【解析】由于关于的不等式>0(≠0)的解集是<1,即当=1时,函数的值为0,故可得到直线与轴的交点坐标.
4. 【答案】C;
【解析】从图象得到,当>-2时,的图象对应的点在函数的图象上面,∴不等式>的解集为>-2.
5. 【答案】D;
【解析】当>4时,>.
6. 【答案】A;
【解析】A、由图象可知<-2时,<,故正确;B、由图象可知<-2时, <,故错误;C、由经过一、三象限是<0,经过四象限是>0,故错误;D、由函数一、二、三象限,可知>0,故错误.
二.填空题
7. 【答案】下;
8. 【答案】=0;<0;;
9. 【答案】① ;
【解析】由图象可知,<0,<0,当时,的图象在的上方,所以,所以只有①正确.
10.【答案】>1;=1;<1;
11.【答案】﹣<x<1;
【解析】解:由题意可得:一次函数图象在y=1的下方时x<﹣1,在y=0的上方时x>﹣,∴关于x的不等式0<kx+b<1的解集是﹣<x<﹣1.
12.【答案】(2,3);
【解析】已知不等式>的解集是<2,则当=2时,-+5=3-3;即当=2时,函数与的函数值相等;因而直线与的交点坐标是:(2,3).
三.解答题
13.【解析】
解:(1)对于,当=0时,=2;当=0时,=2, 即过点(0,2)和点(2,0),过这两点作直线即为的图象; 对于,当=0时,=-4;当=0时,=2, 即过点(0,-4)和点(2,0),过这两点作直线即为的图象. 图象如下图:
(2)从图象得出,当<2时,函数的图象在函数的上方, ∴不等式>的解集为:<2.
14.【解析】
解:(1)设两种费用分别为:y1,y2,
依题意可得:y1=30+0.25x,y2=0.4x;
(2)当x=200时,y1=80,y2=80,两种方式一样.
15.【解析】
解:(1)由y1=﹣x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2,
∵y1=﹣x+1与直线y2=﹣x交于点B,
∴B点的坐标是(﹣1,1.5),
∴△AOB的面积=×2×1.5=1.5;
(2)由(1)可知交点B的坐标是(﹣1,1.5),
由函数图象可知y1>y2时,x>﹣1.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
