北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第11讲 一元一次不等式与不等式组全章复习与巩固(基础)
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第11讲 一元一次不等式与不等式组全章复习与巩固(基础) |
|
|
| 格式 | zip | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-11 00:00:00 | ||
图片预览





文档简介
《一元一次不等式与不等式组》全章复习与巩固(基础)知识讲解
【学习目标】
1.理解不等式的有关概念,掌握不等式的三条基本性质;
2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;
3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组;
4.会根据题中的不等关系建立不等式(组),解决实际应用问题;
5.通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识.
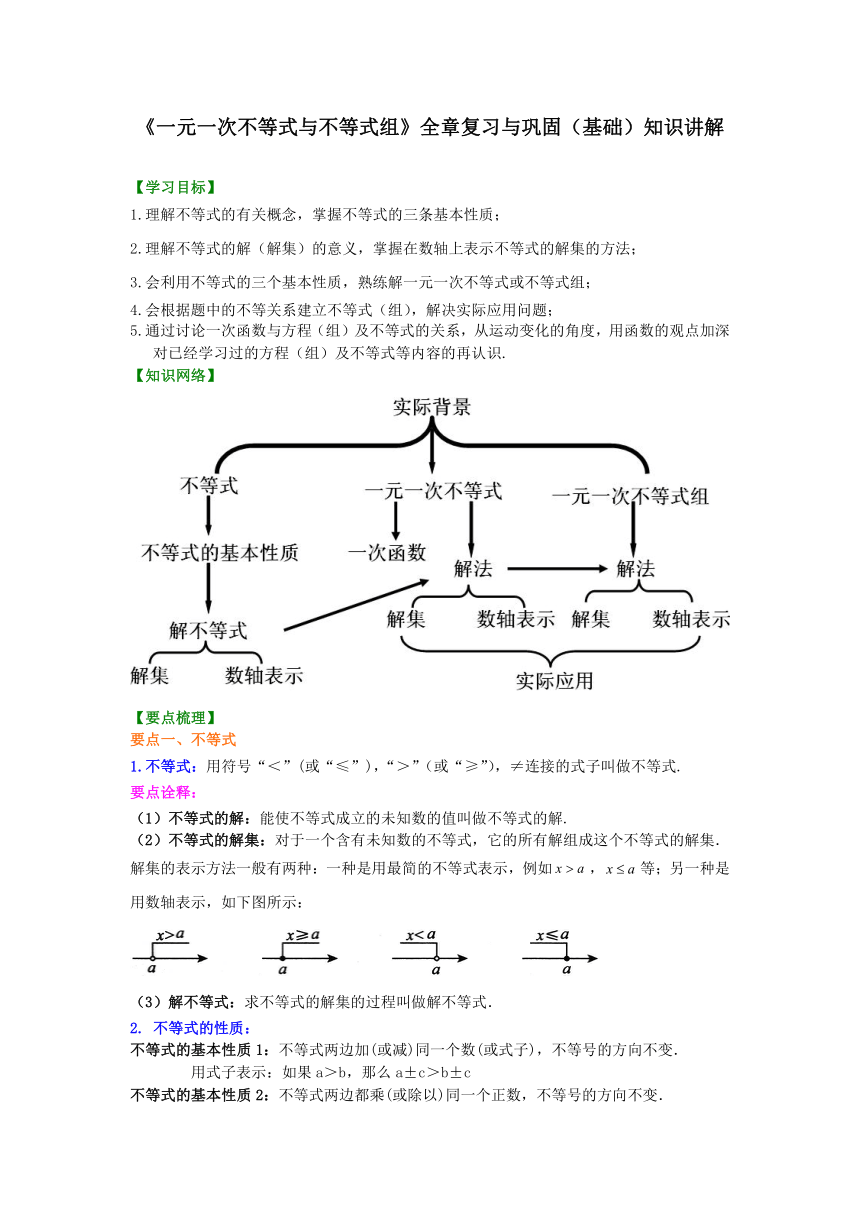
【知识网络】
【要点梳理】
要点一、不等式
1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.
要点诠释:
(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.
(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.
解集的表示方法一般有两种:一种是用最简的不等式表示,例如,等;另一种是用数轴表示,如下图所示:
(3)解不等式:求不等式的解集的过程叫做解不等式.
2. 不等式的性质:
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
用式子表示:如果a>b,那么a±c>b±c
不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
用式子表示:如果a>b,c>0,那么ac>bc(或).
不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
用式子表示:如果a>b,c<0,那么ac<bc(或).
要点二、一元一次不等式
1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式.
要点诠释:ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.
2.解法:
解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 要点诠释:不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.
3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:
(1)审:认真审题,分清已知量、未知量;
(2)设:设出适当的未知数;
(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;
(4)列:根据题中的不等关系,列出不等式;
(5)解:解出所列的不等式的解集;
(6)答:检验是否符合题意,写出答案.
要点诠释:
列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.
要点三、一元一次不等式组 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 要点诠释:
(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.
(2)解不等式组:求不等式组解集的过程,叫做解不等式组.?
(3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集.?
(4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.
要点四、一次函数与一元一次方程、一元一次不等式(组)
方程(组)、不等式问题
函 数 问 题
从“数”的角度看
从“形”的角度看
求关于、的一元一次方程=0(≠0)的解
为何值时,函数的值为0?
确定直线与轴(即直线=0)交点的横坐标.
求关于、的二元一次方程组的解.
为何值时,函数与函数的值相等?
确定直线与直线的交点的坐标.
求关于的一元一次不等式>0(≠0)的解集
为何值时,函数的值大于0?
确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围.
【典型例题】
类型一、不等式
1.用适当的符号语言表达下列关系:
(1)a与5的和是正数.
(2)b与-5的差不是正数.
(3)x的2倍大于x.
(4)2x与1的和小于零.
(5)a的2倍与4的差不少于5.
【答案与解析】
解:(1)a+5>0;(2)b-(-5)≤0; (3)2x>x; (4)2x+1<0;(5)2a-4≥5.
【总结升华】正确运用不等符号翻译表述一些数学描述是学好不等式的关键,要关注一些常见的描述语言,如此处:不是、不少于、不大于…… .
举一反三:
【变式】用适当的符号语言表达下列关系:
(1)y的与3的差是负数.(2)x的与3的差大于2.(3)b的与c的和不大于9.
【答案】(1); (2);(3).
2.用适当的符号填空:
(1)如果a(2)如果a【思路点拨】不等式的基本性质1,2,3.
【答案】(1)<; <;>. (2)<;<;<.
【解析】
(1)在不等式a在不等式a在不等式a(2)在不等式a在a在a【总结升华】刚开始在面对不等式的基本变形时,要不断强化在变形上所运用的具体性质,同时也要逐步积累一些运用性质变形后的化简结果,这样学习到的不等式的基本性质才能落在实处.
举一反三:
【变式1】用适当的符号填空:
(1)7a+6__7a-6;(2)若ac>bc,且c<0,则a b.
【答案】(1)>;(2)<.
【变式2】判断
(1)如果,那么;
(2)如果,那么.
【答案】(1)×;(2)√.
类型二、一元一次不等式? ?
3.(2019?巴中)解不等式:≤﹣1,并把解集表示在数轴上.
【思路点拨】先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
【答案与解析】
解:去分母得,4(2x﹣1)≤3(3x+2)﹣12,
去括号得,8x﹣4≤9x+6﹣12,
移项得,8x﹣9x≤6﹣12+4,
合并同类项得,﹣x≤﹣2,
把x的系数化为1得,x≥2.
在数轴上表示为:
.
【总结升华】本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.
举一反三:
【变式】解不等式,并把解集在数轴上表示出来.
【答案】
解:去分母得5x-1-3x>3,
移项、合并同类项,得2x>4,
系数化为1,得x>2,
解集在数轴上的表示如图所示.
4.某种商品进价为150元,出售时标价为225元,由于销售情况不好,商店准备降价出售,但要保证利润不低于10%,那么商店最多降价多少元出售商品?
【思路点拨】利润=售价-进价,售价=进价+利润=进价×(1+利润率).
【答案与解析】
解:设商店降价元出售该商品,则≥,
解得≤60.
答:商店最多降价60元出售商品。
【总结升华】本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,解答过程中应注意“设”与“答”的区别.
类型三、一元一次不等式组
5.(2019?东丽区二模)解不等式组,并把解集在数轴上表示出来.
【思路点拨】分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则在数轴上将解集表示出来.
【答案与解析】
解:解不等式①,得:x>﹣3,
解不等式②,得:x≤2,
∴不等式组的解集为:﹣3<x≤2,
在数轴上表示不等式组的解集为:
【总结升华】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
举一反三:
【变式1】求不等式组的整数解.
【答案】
解:解不等式-3(x-2)≥4-x,得x≤1,
解不等式,得x>-2,
所以该不等式组的解集为:-2<x≤1,
所以该不等式组的整数解是-1,0,1.
【变式2】(2019?南昌)不等式组的解集是 .
【答案】﹣3<x≤2.
解:,
由①得:x≤2,
由②得:x>﹣3,
则不等式组的解集为﹣3<x≤2.
类型四、一次函数与一元一次方程(组)、不等式
6、如图,平面直角坐标系中画出了函数的图象.
(1)根据图象,求和的值.
(2)在图中画出函数的图象.
(3)求的取值范围,使函数的函数值大于函数的函数值.
【思路点拨】(3)画出函数图象后比较,要使函数的函数值大于函数的函数值,需的图象在图象的上方.
【答案与解析】
解:(1)∵直线经过点(-2,0),(0,2).
∴ 解得
∴.
(2)经过(0,2),(1,0),图象如图所示.
(3)当的函数值大于的函数值时,也就是,解得>0,即的取值范围为>0.
【总结升华】函数图象在上方函数值比函数图象在下方函数值大.
类型五、综合应用
7.若关于x,y的方程组的解满足,求k的整数值.
【思路点拨】从概念出发,解出方程组(用k表示x、y),然后解不等式组.
【答案与解析】
解:解方程组
∵,
解得:.
∴整数k的值为0,1,2.
【总结升华】方程组的未知数是x、y,k在方程组里看成常数.通过求解方程组可以用k表示x、y.方程组的解满足不等式,那么可以将x、y用含k的式子替换,得到关于k的不等式组,可以求出k的取值范围,进而可以求出k的整数值.
举一反三:
【变式】m为何值时,关于x的方程: 的解大于1?
【答案】
解:由,得,
∴,解得.
∴当时,关于x的方程: 的解大于1.
8.某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
【思路点拨】(1)设单独租用35座客车需x辆.根据单独租用35座客车若干辆,则刚好坐满和单独租用55座客车,则可以少租一辆,且余45个空座位,分别表示出总人数,从而列方程求解;(2)设租35座客车y辆,则租55座客车(4-y)辆.根据不等关系:①两种车坐的总人数不小于175人;②租车资金不超过1500元.列不等式组分析求解.
【答案与解析】
解:(1)设单独租用35座客车需x辆,由题意得:
,
解得:.
∴(人).
答:该校八年级参加社会实践活动的人数为175人.
(2)设租35座客车y辆,则租55座客车()辆,由题意得:
,
解这个不等式组,得.
∵取正整数,∴= 2.
∴4- = 4-2 = 2(辆).
∴320×2+400×2 = 1440(元).
所以本次社会实践活动所需车辆的租金为1440元.
【总结升华】本题考查了一元一次方程的应用和一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.
【巩固练习】
一、选择题
1.(2019?河南模拟)下列结论中,正确的是( )
A.若a>b,则< B.若a>b,则a2>b2
C.若a>b,则1﹣a<1﹣b D.若a>b,ac2>bc2
2.(2019?南充)不等式>﹣1的正整数解的个数是( )
A.1个 B.2个 C.3个 D.4个
3.不等式组的解集在数轴上表示正确的是( ).
A B C D
4. 如果关于x的不等式 (a+1)x>a+1的解集为x<1,那么a的取值范围是( ) .
A. a>0 B. a<0 C. a>-1 D. a<-1
5. 一次函数,若=1,则它的图象必经过点( ).
A.(-1,-1) B.(-1, 1) C.(1, -1) D.(1, 1)
6. 以下各式中,一元一次不等式个数为( ).
①;②;③;④;⑤
A. 1 B. 2 C. 3 D. 0
7.直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为( ).
A. B. C. D. 无法确定
8.三个连续自然数的和小于11,这样的自然数组共有( )组. A.1 B.2 C.3 D.4
二、填空题
9.(2019?滨湖区二模)已知不等式3x﹣a≤0的解集为x≤5,则a的值为 .
10.一个不等式的解集如图所示,则这个不等式的正整数解是_____.
11.不等式组的整数解是_______.
12.已知,是正数,则的取值范围 .
13.(2019春?双城市期末)如图,已知函数和y=kx的图象交于点P(﹣4,﹣2),则根据图象可得关于x的不等式>kx的解集为 .
14.关于x的方程2x+3k=1的解是负数,则k的取值范围是_______.
15.若不等式(m-2)x>2的解集是x<,则m的取值范围是_____. 16.小明借到一本有72页的图书,要在10天之内读完,开始2天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天至少要读x页,所列不等式为___________.
三、解答题
17.在数学学习中,及时对知识进行归纳、类比和整理是提高学习效率的有效策略,善于学习的小明在学习解一元一次不等式中,发现它与解一元一次方程有许多相似之处.小明列出了一张对照表: 从表中可以清楚地看出,解一元一次不等式与解一元一次方程有一定的联系,利用这种联系解决下列问题:
(1)若不等式kx>b的解集是x<1,求方程kx=b的解; (2)若方程kx=b的解是x=-1,求不等式kx>b的解集.
18.(2019?遂宁)解不等式组,并将解集在数轴上表示出来.
19.某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案;
(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?
20.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元.小彬经常来该店租碟,若每月租碟数量为张.
(1)写出零星租碟方式应付金额(元)与租碟数量(张)之间的函数关系式;
(2)写出会员卡租碟方式应付金额(元 )与租碟数量(张)之间的函数关系式;
(3)小彬选取哪种租碟方式更合算?
【答案与解析】
一.选择题
1.【答案】C.
【解析】A、当a>0>b时,<,故本选项错误;
B、当a>0,b<0,a<|b|时,a2<b2,故本选项错误;
C、∵a>b,∴﹣a<﹣b,∴1﹣a<1﹣b,故本选项正确;
D、当c=0时,虽然a>b,但是ac2=bc2,故本选项错误.
2. 【答案】D;
【解析】解:去分母得:3(x+1)>2(2x+2)﹣6,
去括号得:3x+3>4x+4﹣6,
移项得:3x﹣4x>4﹣6﹣3,
合并同类项得:﹣x>﹣5,
系数化为1得:x<5,
故不等式的正整数解有1、2、3、4这4个,
故选:D.
3. 【答案】B;
4. 【答案】D;
【解析】不等号的方向改变,说明a+1<0,即a<﹣1.
5. 【答案】D;
【解析】当=1时,=1,故它的图象过点(1,1).
6. 【答案】B;
【解析】是一元一次不等式的是①和⑤.
7. 【答案】B;
【解析】当<-1时,直线在直线的上方.
8. 【答案】C;
【解析】,解得n=0、1、2,共3组.
二.填空题
9.【答案】15.
【解析】解不等式3x﹣a≤0得,x≤,∵不等式的解集为x≤5,∴=5,解得a=15.
10. 【答案】1、2;
【解析】由图可得,所以正整数有1、2.
11. 【答案】-1,0;
【解析】不等式组的解集为,整数解为-1,0.
12. 【答案】;
【解析】由,解得,化简得.
13. 【答案】x<﹣4;
【解析】解:当x<﹣4时,的图象都在y=kx的图象上方,
所以关于x的不等式>kx的解集为x<﹣4.
故答案为:x<﹣4.
14. 【答案】;
【解析】解方程得,则.
15. 【答案】m<2;
【解析】由不等式的基本性质3得,m-2<0.
16. 【答案】(或:等);
【解析】答案不唯一.
三.解答题
17.【解析】
解:(1).
(2)当时, 当
18.【解析】
解:,
由①得,x>﹣3,
由②得,x≤2,
故此不等式组的解集为:﹣3<x≤2.
在数轴上表示为:
19.【解析】
解:(1)设租用甲车x辆,则租用乙车(10-x)辆.
由题意得 解得4≤x≤7.5.
因为x取整数,所以x=4,5,6,7.则相应地,10-x=6,5,4,3.
因此,有四种租车方案,分别是:
①租用甲车4辆,乙车6辆;
②租用甲车5辆,乙车5辆;
③租用甲车6辆,乙车4辆;
④租用甲车7辆,乙车3辆.
(2)租车费用分别为:
①4×2000+6×1800=18800(元);
②5×2000+5×1800=19000(元);
③6×2000+4×1800=19200(元);
④7×2000+3×1800=19400(元).
因为18800<19000<19200<19400,所以,方案①租甲车4辆,乙车6辆费用最省.
20.【解析】
解:(1).
(2).
所以,当租碟少于20张时,选零星租碟方式合算;当租碟20张时,两种方式一样;当租碟大于20张时,选会员卡租碟合算.
【学习目标】
1.理解不等式的有关概念,掌握不等式的三条基本性质;
2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;
3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组;
4.会根据题中的不等关系建立不等式(组),解决实际应用问题;
5.通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识.
【知识网络】
【要点梳理】
要点一、不等式
1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.
要点诠释:
(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.
(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.
解集的表示方法一般有两种:一种是用最简的不等式表示,例如,等;另一种是用数轴表示,如下图所示:
(3)解不等式:求不等式的解集的过程叫做解不等式.
2. 不等式的性质:
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
用式子表示:如果a>b,那么a±c>b±c
不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
用式子表示:如果a>b,c>0,那么ac>bc(或).
不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
用式子表示:如果a>b,c<0,那么ac<bc(或).
要点二、一元一次不等式
1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式.
要点诠释:ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.
2.解法:
解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 要点诠释:不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.
3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:
(1)审:认真审题,分清已知量、未知量;
(2)设:设出适当的未知数;
(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;
(4)列:根据题中的不等关系,列出不等式;
(5)解:解出所列的不等式的解集;
(6)答:检验是否符合题意,写出答案.
要点诠释:
列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.
要点三、一元一次不等式组 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 要点诠释:
(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.
(2)解不等式组:求不等式组解集的过程,叫做解不等式组.?
(3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集.?
(4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.
要点四、一次函数与一元一次方程、一元一次不等式(组)
方程(组)、不等式问题
函 数 问 题
从“数”的角度看
从“形”的角度看
求关于、的一元一次方程=0(≠0)的解
为何值时,函数的值为0?
确定直线与轴(即直线=0)交点的横坐标.
求关于、的二元一次方程组的解.
为何值时,函数与函数的值相等?
确定直线与直线的交点的坐标.
求关于的一元一次不等式>0(≠0)的解集
为何值时,函数的值大于0?
确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围.
【典型例题】
类型一、不等式
1.用适当的符号语言表达下列关系:
(1)a与5的和是正数.
(2)b与-5的差不是正数.
(3)x的2倍大于x.
(4)2x与1的和小于零.
(5)a的2倍与4的差不少于5.
【答案与解析】
解:(1)a+5>0;(2)b-(-5)≤0; (3)2x>x; (4)2x+1<0;(5)2a-4≥5.
【总结升华】正确运用不等符号翻译表述一些数学描述是学好不等式的关键,要关注一些常见的描述语言,如此处:不是、不少于、不大于…… .
举一反三:
【变式】用适当的符号语言表达下列关系:
(1)y的与3的差是负数.(2)x的与3的差大于2.(3)b的与c的和不大于9.
【答案】(1); (2);(3).
2.用适当的符号填空:
(1)如果a
【答案】(1)<; <;>. (2)<;<;<.
【解析】
(1)在不等式a
举一反三:
【变式1】用适当的符号填空:
(1)7a+6__7a-6;(2)若ac>bc,且c<0,则a b.
【答案】(1)>;(2)<.
【变式2】判断
(1)如果,那么;
(2)如果,那么.
【答案】(1)×;(2)√.
类型二、一元一次不等式? ?
3.(2019?巴中)解不等式:≤﹣1,并把解集表示在数轴上.
【思路点拨】先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
【答案与解析】
解:去分母得,4(2x﹣1)≤3(3x+2)﹣12,
去括号得,8x﹣4≤9x+6﹣12,
移项得,8x﹣9x≤6﹣12+4,
合并同类项得,﹣x≤﹣2,
把x的系数化为1得,x≥2.
在数轴上表示为:
.
【总结升华】本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.
举一反三:
【变式】解不等式,并把解集在数轴上表示出来.
【答案】
解:去分母得5x-1-3x>3,
移项、合并同类项,得2x>4,
系数化为1,得x>2,
解集在数轴上的表示如图所示.
4.某种商品进价为150元,出售时标价为225元,由于销售情况不好,商店准备降价出售,但要保证利润不低于10%,那么商店最多降价多少元出售商品?
【思路点拨】利润=售价-进价,售价=进价+利润=进价×(1+利润率).
【答案与解析】
解:设商店降价元出售该商品,则≥,
解得≤60.
答:商店最多降价60元出售商品。
【总结升华】本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,解答过程中应注意“设”与“答”的区别.
类型三、一元一次不等式组
5.(2019?东丽区二模)解不等式组,并把解集在数轴上表示出来.
【思路点拨】分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则在数轴上将解集表示出来.
【答案与解析】
解:解不等式①,得:x>﹣3,
解不等式②,得:x≤2,
∴不等式组的解集为:﹣3<x≤2,
在数轴上表示不等式组的解集为:
【总结升华】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
举一反三:
【变式1】求不等式组的整数解.
【答案】
解:解不等式-3(x-2)≥4-x,得x≤1,
解不等式,得x>-2,
所以该不等式组的解集为:-2<x≤1,
所以该不等式组的整数解是-1,0,1.
【变式2】(2019?南昌)不等式组的解集是 .
【答案】﹣3<x≤2.
解:,
由①得:x≤2,
由②得:x>﹣3,
则不等式组的解集为﹣3<x≤2.
类型四、一次函数与一元一次方程(组)、不等式
6、如图,平面直角坐标系中画出了函数的图象.
(1)根据图象,求和的值.
(2)在图中画出函数的图象.
(3)求的取值范围,使函数的函数值大于函数的函数值.
【思路点拨】(3)画出函数图象后比较,要使函数的函数值大于函数的函数值,需的图象在图象的上方.
【答案与解析】
解:(1)∵直线经过点(-2,0),(0,2).
∴ 解得
∴.
(2)经过(0,2),(1,0),图象如图所示.
(3)当的函数值大于的函数值时,也就是,解得>0,即的取值范围为>0.
【总结升华】函数图象在上方函数值比函数图象在下方函数值大.
类型五、综合应用
7.若关于x,y的方程组的解满足,求k的整数值.
【思路点拨】从概念出发,解出方程组(用k表示x、y),然后解不等式组.
【答案与解析】
解:解方程组
∵,
解得:.
∴整数k的值为0,1,2.
【总结升华】方程组的未知数是x、y,k在方程组里看成常数.通过求解方程组可以用k表示x、y.方程组的解满足不等式,那么可以将x、y用含k的式子替换,得到关于k的不等式组,可以求出k的取值范围,进而可以求出k的整数值.
举一反三:
【变式】m为何值时,关于x的方程: 的解大于1?
【答案】
解:由,得,
∴,解得.
∴当时,关于x的方程: 的解大于1.
8.某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
【思路点拨】(1)设单独租用35座客车需x辆.根据单独租用35座客车若干辆,则刚好坐满和单独租用55座客车,则可以少租一辆,且余45个空座位,分别表示出总人数,从而列方程求解;(2)设租35座客车y辆,则租55座客车(4-y)辆.根据不等关系:①两种车坐的总人数不小于175人;②租车资金不超过1500元.列不等式组分析求解.
【答案与解析】
解:(1)设单独租用35座客车需x辆,由题意得:
,
解得:.
∴(人).
答:该校八年级参加社会实践活动的人数为175人.
(2)设租35座客车y辆,则租55座客车()辆,由题意得:
,
解这个不等式组,得.
∵取正整数,∴= 2.
∴4- = 4-2 = 2(辆).
∴320×2+400×2 = 1440(元).
所以本次社会实践活动所需车辆的租金为1440元.
【总结升华】本题考查了一元一次方程的应用和一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.
【巩固练习】
一、选择题
1.(2019?河南模拟)下列结论中,正确的是( )
A.若a>b,则< B.若a>b,则a2>b2
C.若a>b,则1﹣a<1﹣b D.若a>b,ac2>bc2
2.(2019?南充)不等式>﹣1的正整数解的个数是( )
A.1个 B.2个 C.3个 D.4个
3.不等式组的解集在数轴上表示正确的是( ).
A B C D
4. 如果关于x的不等式 (a+1)x>a+1的解集为x<1,那么a的取值范围是( ) .
A. a>0 B. a<0 C. a>-1 D. a<-1
5. 一次函数,若=1,则它的图象必经过点( ).
A.(-1,-1) B.(-1, 1) C.(1, -1) D.(1, 1)
6. 以下各式中,一元一次不等式个数为( ).
①;②;③;④;⑤
A. 1 B. 2 C. 3 D. 0
7.直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解为( ).
A. B. C. D. 无法确定
8.三个连续自然数的和小于11,这样的自然数组共有( )组. A.1 B.2 C.3 D.4
二、填空题
9.(2019?滨湖区二模)已知不等式3x﹣a≤0的解集为x≤5,则a的值为 .
10.一个不等式的解集如图所示,则这个不等式的正整数解是_____.
11.不等式组的整数解是_______.
12.已知,是正数,则的取值范围 .
13.(2019春?双城市期末)如图,已知函数和y=kx的图象交于点P(﹣4,﹣2),则根据图象可得关于x的不等式>kx的解集为 .
14.关于x的方程2x+3k=1的解是负数,则k的取值范围是_______.
15.若不等式(m-2)x>2的解集是x<,则m的取值范围是_____. 16.小明借到一本有72页的图书,要在10天之内读完,开始2天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天至少要读x页,所列不等式为___________.
三、解答题
17.在数学学习中,及时对知识进行归纳、类比和整理是提高学习效率的有效策略,善于学习的小明在学习解一元一次不等式中,发现它与解一元一次方程有许多相似之处.小明列出了一张对照表: 从表中可以清楚地看出,解一元一次不等式与解一元一次方程有一定的联系,利用这种联系解决下列问题:
(1)若不等式kx>b的解集是x<1,求方程kx=b的解; (2)若方程kx=b的解是x=-1,求不等式kx>b的解集.
18.(2019?遂宁)解不等式组,并将解集在数轴上表示出来.
19.某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案;
(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?
20.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元.小彬经常来该店租碟,若每月租碟数量为张.
(1)写出零星租碟方式应付金额(元)与租碟数量(张)之间的函数关系式;
(2)写出会员卡租碟方式应付金额(元 )与租碟数量(张)之间的函数关系式;
(3)小彬选取哪种租碟方式更合算?
【答案与解析】
一.选择题
1.【答案】C.
【解析】A、当a>0>b时,<,故本选项错误;
B、当a>0,b<0,a<|b|时,a2<b2,故本选项错误;
C、∵a>b,∴﹣a<﹣b,∴1﹣a<1﹣b,故本选项正确;
D、当c=0时,虽然a>b,但是ac2=bc2,故本选项错误.
2. 【答案】D;
【解析】解:去分母得:3(x+1)>2(2x+2)﹣6,
去括号得:3x+3>4x+4﹣6,
移项得:3x﹣4x>4﹣6﹣3,
合并同类项得:﹣x>﹣5,
系数化为1得:x<5,
故不等式的正整数解有1、2、3、4这4个,
故选:D.
3. 【答案】B;
4. 【答案】D;
【解析】不等号的方向改变,说明a+1<0,即a<﹣1.
5. 【答案】D;
【解析】当=1时,=1,故它的图象过点(1,1).
6. 【答案】B;
【解析】是一元一次不等式的是①和⑤.
7. 【答案】B;
【解析】当<-1时,直线在直线的上方.
8. 【答案】C;
【解析】,解得n=0、1、2,共3组.
二.填空题
9.【答案】15.
【解析】解不等式3x﹣a≤0得,x≤,∵不等式的解集为x≤5,∴=5,解得a=15.
10. 【答案】1、2;
【解析】由图可得,所以正整数有1、2.
11. 【答案】-1,0;
【解析】不等式组的解集为,整数解为-1,0.
12. 【答案】;
【解析】由,解得,化简得.
13. 【答案】x<﹣4;
【解析】解:当x<﹣4时,的图象都在y=kx的图象上方,
所以关于x的不等式>kx的解集为x<﹣4.
故答案为:x<﹣4.
14. 【答案】;
【解析】解方程得,则.
15. 【答案】m<2;
【解析】由不等式的基本性质3得,m-2<0.
16. 【答案】(或:等);
【解析】答案不唯一.
三.解答题
17.【解析】
解:(1).
(2)当时, 当
18.【解析】
解:,
由①得,x>﹣3,
由②得,x≤2,
故此不等式组的解集为:﹣3<x≤2.
在数轴上表示为:
19.【解析】
解:(1)设租用甲车x辆,则租用乙车(10-x)辆.
由题意得 解得4≤x≤7.5.
因为x取整数,所以x=4,5,6,7.则相应地,10-x=6,5,4,3.
因此,有四种租车方案,分别是:
①租用甲车4辆,乙车6辆;
②租用甲车5辆,乙车5辆;
③租用甲车6辆,乙车4辆;
④租用甲车7辆,乙车3辆.
(2)租车费用分别为:
①4×2000+6×1800=18800(元);
②5×2000+5×1800=19000(元);
③6×2000+4×1800=19200(元);
④7×2000+3×1800=19400(元).
因为18800<19000<19200<19400,所以,方案①租甲车4辆,乙车6辆费用最省.
20.【解析】
解:(1).
(2).
所以,当租碟少于20张时,选零星租碟方式合算;当租碟20张时,两种方式一样;当租碟大于20张时,选会员卡租碟合算.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
