高中物理教科版必修二学案:第3章 章末复习课 Word版含答案
文档属性
| 名称 | 高中物理教科版必修二学案:第3章 章末复习课 Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-10-11 00:00:00 | ||
图片预览




文档简介
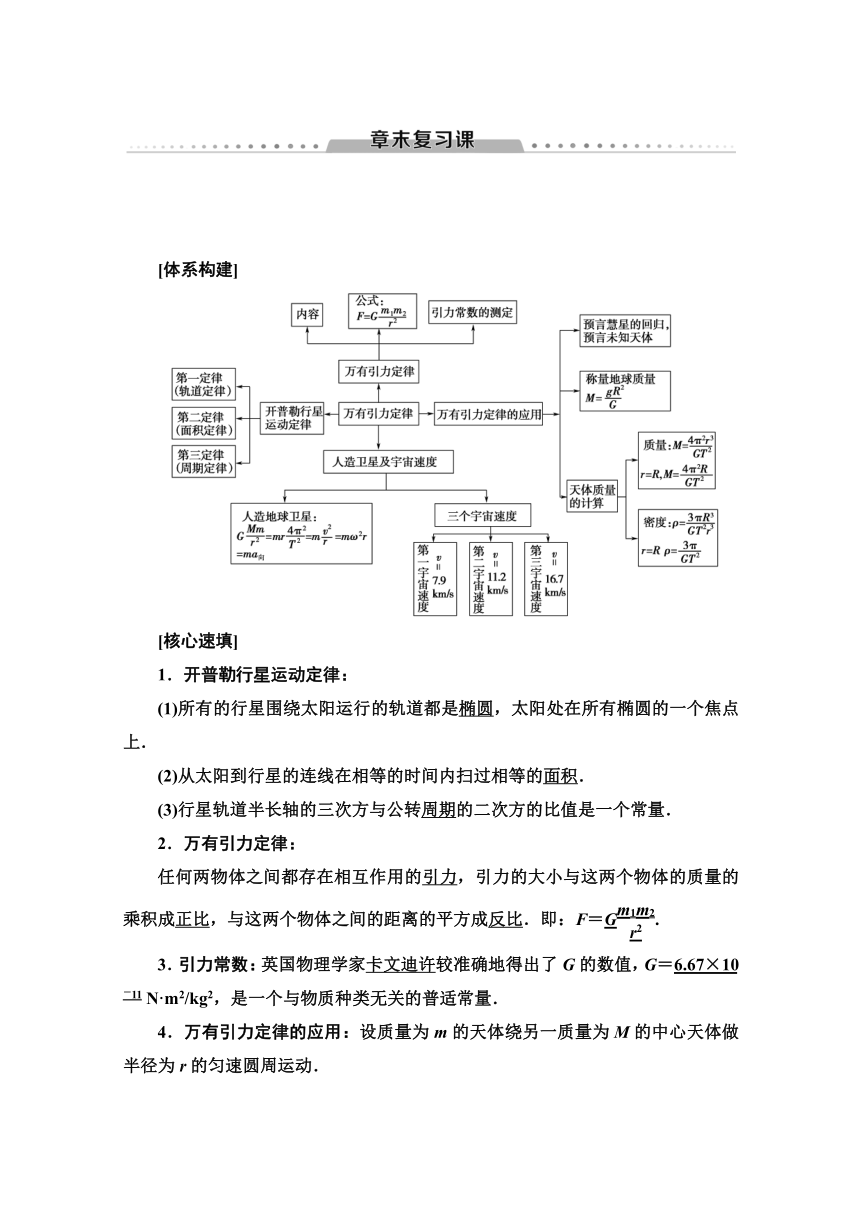
[体系构建]
[核心速填]
1.开普勒行星运动定律:
(1)所有的行星围绕太阳运行的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
(2)从太阳到行星的连线在相等的时间内扫过相等的面积.
(3)行星轨道半长轴的三次方与公转周期的二次方的比值是一个常量.
2.万有引力定律:
任何两物体之间都存在相互作用的引力,引力的大小与这两个物体的质量的乘积成正比,与这两个物体之间的距离的平方成反比.即:F=G.
3.引力常数:英国物理学家卡文迪许较准确地得出了G的数值,G=6.67×10-11 N·m2/kg2,是一个与物质种类无关的普适常量.
4.万有引力定律的应用:设质量为m的天体绕另一质量为M的中心天体做半径为r的匀速圆周运动.
(1)G=m得v=,r越大v越小.
(2)G=mω2r得ω=,r越大,ω越小.
(3)G=mr得T=2π,r越大,T越大.
(4)G=ma向得a向=,r越大,a向越小.
(5)忽略地球自转时,G=mg得gR2=GM,该式称为“黄金代换式”.
5.宇宙速度:
(1)第一宇宙速度
使卫星能环绕地球运行所需的最大速度,其大小为v1=7.9_km/s,又称环绕速度.
(2)第二宇宙速度
使人造卫星脱离地球的引力束缚,不再绕地球运行,从地球表面发射所需的最小速度,其大小为v2=11.2_km/s,又称脱离速度.
(3)第三宇宙速度
使物体脱离太阳的束缚而飞离太阳系,从地球表面发射所需的最小速度,其大小为v3=16.7_km/s,也叫逃逸速度.
万有引力定律的综合应用
万有引力定律揭示了自然界中普遍存在的一种相互作用规律,将地面上物体的运动与天体的运动统一起来,其分析方法不是很复杂,无论是行星绕太阳的运动,还是卫星绕行星的运动,将它们的运动均看作是匀速圆周运动,紧紧抓住“万有引力提供向心力”这一点来进行,即向心力=万有引力.
可表示为m=mω2r=mr=ma=G.
在应用时应注意区分以下模糊概念
1.天体半径和卫星轨道半径的区别
天体半径反映天体大小,而卫星轨道半径是卫星绕天体做圆周运动的半径,一般卫星的轨道半径总大于该天体的半径,只有当卫星贴近天体表面运行时,可近似认为卫星轨道半径等于天体半径.
2.赤道上物体的加速度与卫星的加速度的区别
赤道上物体受地球的万有引力作用,万有引力的作用产生两个效果,一个分力提供物体随地球自转做圆周运动的向心力,另一个分力才是重力,由于重力近似等于万有引力,所以赤道上物体的加速度很小.而卫星的向心加速度由万有引力提供.
【例1】 a是地球赤道上一幢建筑,b是在赤道平面内做匀速圆周运动、距地面9.6×106 m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图甲所示),经48 h,a、b、c的大致位置是图乙中的(取地球半径R=6.4×106 m,地球表面重力加速度g=10 m/s2,π=)( )
甲 乙
B [由G=m(R+h)可得T==,代入数据可求得b的周期为20 000 s.从图甲位置经48 h后,同步卫星c应位于a的正上方,而卫星b绕地球做完整圆周运动的次数为8.63次,可以判断只有B符合要求.]
1.如图所示,在同一轨道平面上的几个人造地球卫星A、B、C绕地球做匀速圆周运动,某一时刻它们恰好在同一直线上,下列说法中正确的是( )
A.根据v=可知,运行速度满足vA>vB>vC
B.运转角速度满足ωA>ωB>ωC
C.向心加速度满足aA
C [由G=m得,v=,r大,则v小,故vA
天体运动的规律
分析处理天体运动问题,要抓住“一个模型”、应用“两个思路”、区分“三个不同”.
1.一个模型
无论是自然天体(如行星、月球等),还是人造天体(如人造卫星、空间站等),只要天体的运动轨迹为圆形,就可将其简化为质点的匀速圆周运动.
2.两个思路
(1)所有做圆周运动的天体,所需的向心力都来自万有引力.因此,向心力等于万有引力,据此所列方程是研究天体运动的基本关系式,即
G=m=mω2r=mr=man.
(2)不考虑地球或天体自转影响时,物体在地球或天体表面受到的万有引力约等于物体的重力,即G=mg,变形得GM=gR2,此式通常称为“黄金代换式”.
3.三个不同
(1)不同公式中r的含义不同.
在万有引力定律公式中,r的含义是两质点间的距离;在向心力公式(F=m=mω2r)中,r的含义是质点运动的轨道半径.
当一个天体绕另一个天体做匀速圆周运动时,两式中的r相等.
(2)运行速度、发射速度和宇宙速度的含义不同.
三种速度的比较,如下表所示
比较项
概念
大小
影响因素
运行速度
卫星绕中心天体做匀速圆周运动的速度
v=
轨道半径r越大,v越小
发射速度
在地面上发射卫星的速度
大于或等于
7.9 km/s
卫星的发射高度越高,发射速度越大
宇宙速度
实现某种效果所需的最小卫星发射速度
7.9 km/s
11.2 km/s
16.7 km/s
不同卫星发射要求不同
(3)卫星的向心加速度a、地球表面的重力加速度g、在地球表面的物体随地球自转做匀速圆周运动的向心加速度a′的含义不同.
①绕地球做匀速圆周运动的卫星的运行加速度或向心加速度a,由G=ma,得a=,其中r为卫星的轨道半径.
②若不考虑地球自转的影响,地球表面的重力加速度为g=,其中R为地球的半径.
③地球表面的物体随地球自转做匀速圆周运动的向心加速度a′=ω2Rcos θ,其中ω、R分别是地球的自转角速度和半径,θ是物体所在位置的纬度值.
【例2】 (多选)已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
A.卫星距地面的高度为
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时受到的向心力大小为G
D.卫星运行的向心加速度小于地球表面的重力加速度
BD [对同步卫星由万有引力提供向心力有G=m(R+h),所以h=-R,A错误;第一宇宙速度是最大的环绕速度,B正确;同步卫星运动的向心力等于万有引力,应为F=,C错误;同步卫星的向心加速度为a同=,地球表面的重力加速度a表=,知a表>a同,D正确.]
[一语通关] (1(分析该类问题的关键是抓住“万有引力提供向心力”这一主线.
(2(定量计算时,除抓住以上主线外,有时要借助于“黄金代换式”才能顺利解决问题.
2.质量相等的甲、乙两颗卫星分别贴近某星球表面和地球表面围绕其做匀速圆周运动,已知该星球和地球的密度相同,半径分别为R和r,则( )
A.甲、乙两颗卫星的加速度之比等于R∶r
B.甲、乙两颗卫星所受的向心力之比等于1∶1
C.甲、乙两颗卫星的线速度之比等于1∶1
D.甲、乙两颗卫星的周期之比等于R∶r
A [由F=G和M=ρπR3可得万有引力F=GπRmρ,又由牛顿第二定律F=ma可得,A正确;卫星绕星球表面做匀速圆周运动时,万有引力等于向心力,因此B错误;由F=GπRmρ,F=m可得,选项C错误;由F=GπRmρ,F=mR可知,周期之比为1∶1,故D错误.]
天体运动中的多星问题
1.双星问题
众多的天体中如果有两颗恒星,它们靠得较近,在万有引力作用下绕着中间的某一点共同转动,这样的两颗恒星称为双星.
如图所示为质量分别是m1和m2的两颗相距较近的恒星.它们间的距离为L.此双星问题的特点是:
(1)两星的运行轨道为同心圆;
(2)两星的运动半径之和等于它们间的距离,即r1+r2=L;
(3)两星的转动周期(角速度)相同.
由于m1r1ω2=m2r2ω2,即m1r1=m2r2,所以双星中某星的运动半径与其质量成反比.
若已知双星的运动周期T,由G=m1r1和G=m2r2可求得两星的总质量为m1+m2=.
2.三星问题
三星问题中,其中任一颗星都在另两颗星的共同作用下做匀速圆周运动,要明确万有引力中的距离和匀速圆周运动中的半径,并且还要明确二者之间的关系,找准关系往往是解题的突破口.
3.四星问题
四星问题中,其中任一颗星都在另三颗星的共同作用下做匀速圆周运动.运动过程中,四颗星的相对位置不变,具有相同的转动周期,共同绕正方形对角线的交点做匀速圆周运动.
【例3】 宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设每个星体的质量均为m.
(1)试求第一种形式下,星体运动的线速度和周期.
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
(3)若是四星,请画出其星体的位置.
[解析] (1)对于第一种运动情况,以某个运动星体为研究对象,根据牛顿第二定律和万有引力定律有F1=,F2=,F合=F1+F2=
运动星体的线速度v=,
由T=得T=4π.
(2)设第二种形式星体之间的距离为r,则三个星体做圆周运动的半径为R′=.由于星体做圆周运动所需的向心力靠其他两个星体的万有引力的合力提供,由力的合成和牛顿运动定律得
F合=2 cos 30°,F合=mR′,r=R.
(3)四颗星位于正方形的四个顶点上,围绕正方形的中心做圆轨道运行.
[答案] 见解析
3.宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动而不会因万有引力的作用吸引到一起.
(1)试证明它们的轨道半径之比、线速度之比都等于质量的反比.
(2)设两者的质量分别为m1和m2,两者相距L,试写出它们角速度的表达式.
[解析] (1)证明:两天体绕同一点做匀速圆周运动的角速度ω一定相同.它们做匀速圆周运动的向心力由它们之间的万有引力提供,所以两天体与它们的圆心总是在一条直线上.
设两者的圆心为O点,轨道半径分别为R1和R2,如图所示.对两天体,由万有引力定律可得
G=m1ω2R1 ①
G=m2ω2R2 ②
所以=,所以===,即它们的轨道半径、线速度之比都等于质量的反比.
(2)由①②两式相加得G=ω2(R1+R2)③
因为R1+R2=L,所以ω=.
[答案] (1)见解析 (2)ω=
