人教A版高中数学选修1-12.3.1抛物线及其标准方程教案
文档属性
| 名称 | 人教A版高中数学选修1-12.3.1抛物线及其标准方程教案 |  | |
| 格式 | zip | ||
| 文件大小 | 23.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 20:16:28 | ||
图片预览

文档简介
2.1.6 抛物线及其标准方程
一、教学目标:
知识与技能:
了解抛物线的定义,几何图形和标准方程
会利用定义和标准方程求焦点坐标和准线方程
理解P的意义
过程与方法
通过“观察”、“思考”、“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,使学生学会数学思考与推理,学会反思与感悟,形成良好的数学观。并进一步感受坐标法及数形结合的思想。
情感态度与价值观
进一步培养学生合作、交流的能力和团队精神,培养学生实事求是、善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学习活动,养成良好的学习习惯;同时通过欣赏生活中一些抛物线型建筑,不但加强了学生对抛物线的感性认识,而且使学生受到美的享受,陶冶了情操。
二、教学重点.难点
重点:抛物线定义的灵活应用以及抛物线标准方程的求法.
难点:抛物线定义的灵活应用以及抛物线标准方程的求法.
三、学情分析
对于高二的学生,在初中已经学过二次函数的图像是抛物线,研究过抛物线的顶点坐标、对称轴等问题,而我们现在学的圆锥曲线是要从最基本的图形入手来研究抛物线的特征,学生有了对抛物线的简单认识,所以学习这节课是对以前所学内容的进一步加深,符合我们的教育思路“由浅入深,步步深入”。
四、教学方法
本节课主要通过数形结合,类比的思想,运用现代化教学手段,通过观察,分析,归纳出双曲线的几何性质,在教学过程中可采取设疑提问,重点讲解,归纳总结,引导学生积极 思考,鼓励学生合作交流。
五、教学过程
新课引入
1.创设情境,引入课题
教师导语:我们之前学习了圆锥曲线中的椭圆,双曲线,今天我们开始学习第四节第一小节:抛物线及其标准方程.
六、自主学习
1.抛物线定义:
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线.
抛物线的定义可以从以下几个方面理解、掌握:?
(1)抛物线的定义还可叙述为“平面内与一个定点F和一条直线l的距离的比等于1的点的轨迹叫做抛物线”.?
(2)定义的实质可归结为“一动三定”,一个动点,设为M;一个定点F,叫做抛物线的焦点;一条定直线l,叫做抛物线的准线;一个定值,即点M与点F的距离和它到直线l的距离之比等于1,为离心率.?
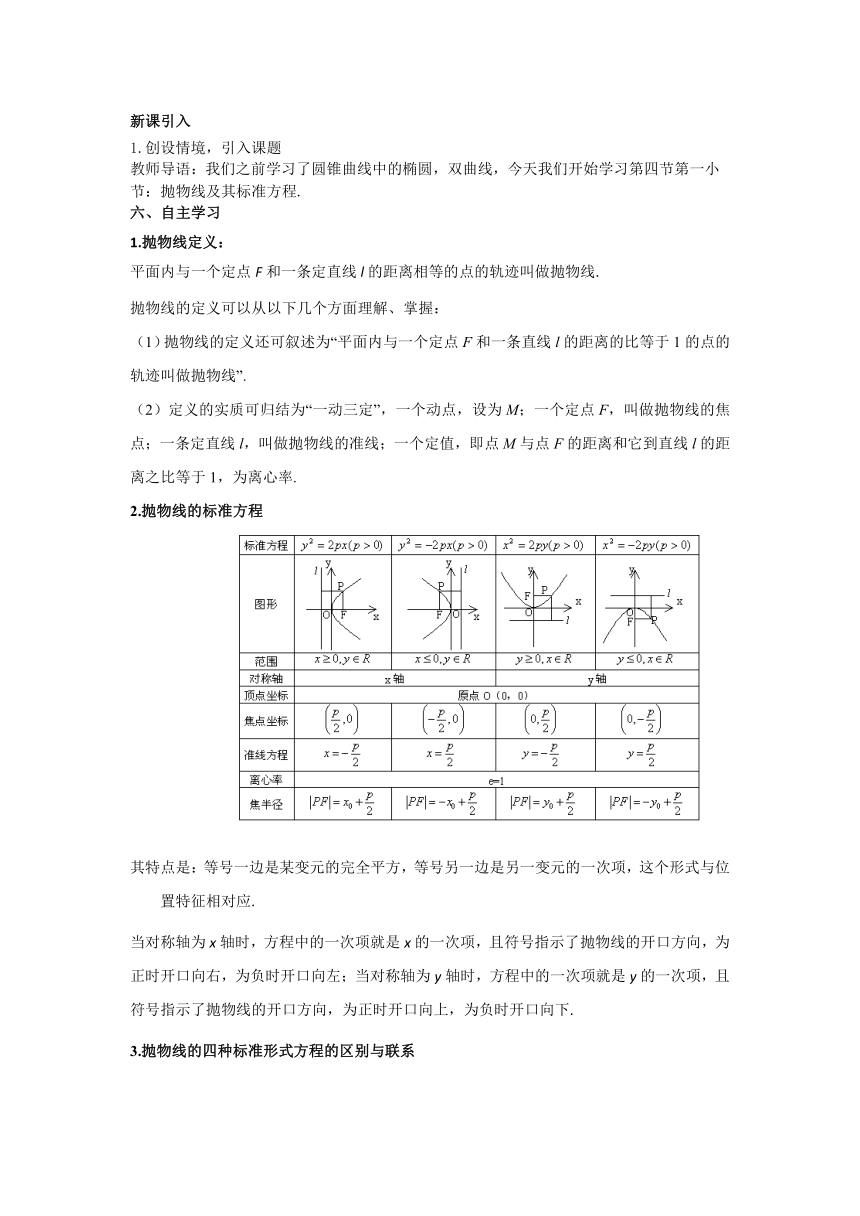
2.抛物线的标准方程
其特点是:等号一边是某变元的完全平方,等号另一边是另一变元的一次项,这个形式与位置特征相对应.?
当对称轴为x轴时,方程中的一次项就是x的一次项,且符号指示了抛物线的开口方向,为正时开口向右,为负时开口向左;当对称轴为y轴时,方程中的一次项就是y的一次项,且符号指示了抛物线的开口方向,为正时开口向上,为负时开口向下.
3.抛物线的四种标准形式方程的区别与联系?
(1)相同点:①原点在抛物线上;②对称轴为坐标轴;?③焦点的非零坐标(指或)是一次项系数的;④准线与对称轴垂直且垂足与焦点关于坐标原点对称;⑤p都是代表焦点到准线的距离(称p为焦参数),∴p>0.?
(2)不同点;对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2,即方程右端一次项的变量与焦点所在坐标轴的名称相同,一次项系数的符号决定抛物线的开口方向.
典型例题:
已知抛物线的标准方程是,求它的焦点坐标和准线方程;
已知抛物线的焦点是,求它的标准方程.
例3、求过点的抛物线的标准方程.
五、当堂检测
1、已知抛物线的标准方程是,求它的焦点坐标和准线方程。
已知抛物线的焦点是,求它的标准方程。
3、根据下列条件写出抛物线的标准方程:
(1)焦点是(2)准线方程是(3)焦点到准线的距离是2
【设计意图:通过三种层次的反馈例练,由浅入深,逐渐达到运用新知的目的,同时反馈学生学习理解的
程度,进行学习监控和补救.】
六、课堂小结
1.知识建构
2.能力提高
3.课堂体验
七、课时练与测
八、教学反思
一、教学目标:
知识与技能:
了解抛物线的定义,几何图形和标准方程
会利用定义和标准方程求焦点坐标和准线方程
理解P的意义
过程与方法
通过“观察”、“思考”、“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,使学生学会数学思考与推理,学会反思与感悟,形成良好的数学观。并进一步感受坐标法及数形结合的思想。
情感态度与价值观
进一步培养学生合作、交流的能力和团队精神,培养学生实事求是、善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学习活动,养成良好的学习习惯;同时通过欣赏生活中一些抛物线型建筑,不但加强了学生对抛物线的感性认识,而且使学生受到美的享受,陶冶了情操。
二、教学重点.难点
重点:抛物线定义的灵活应用以及抛物线标准方程的求法.
难点:抛物线定义的灵活应用以及抛物线标准方程的求法.
三、学情分析
对于高二的学生,在初中已经学过二次函数的图像是抛物线,研究过抛物线的顶点坐标、对称轴等问题,而我们现在学的圆锥曲线是要从最基本的图形入手来研究抛物线的特征,学生有了对抛物线的简单认识,所以学习这节课是对以前所学内容的进一步加深,符合我们的教育思路“由浅入深,步步深入”。
四、教学方法
本节课主要通过数形结合,类比的思想,运用现代化教学手段,通过观察,分析,归纳出双曲线的几何性质,在教学过程中可采取设疑提问,重点讲解,归纳总结,引导学生积极 思考,鼓励学生合作交流。
五、教学过程
新课引入
1.创设情境,引入课题
教师导语:我们之前学习了圆锥曲线中的椭圆,双曲线,今天我们开始学习第四节第一小节:抛物线及其标准方程.
六、自主学习
1.抛物线定义:
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线.
抛物线的定义可以从以下几个方面理解、掌握:?
(1)抛物线的定义还可叙述为“平面内与一个定点F和一条直线l的距离的比等于1的点的轨迹叫做抛物线”.?
(2)定义的实质可归结为“一动三定”,一个动点,设为M;一个定点F,叫做抛物线的焦点;一条定直线l,叫做抛物线的准线;一个定值,即点M与点F的距离和它到直线l的距离之比等于1,为离心率.?
2.抛物线的标准方程
其特点是:等号一边是某变元的完全平方,等号另一边是另一变元的一次项,这个形式与位置特征相对应.?
当对称轴为x轴时,方程中的一次项就是x的一次项,且符号指示了抛物线的开口方向,为正时开口向右,为负时开口向左;当对称轴为y轴时,方程中的一次项就是y的一次项,且符号指示了抛物线的开口方向,为正时开口向上,为负时开口向下.
3.抛物线的四种标准形式方程的区别与联系?
(1)相同点:①原点在抛物线上;②对称轴为坐标轴;?③焦点的非零坐标(指或)是一次项系数的;④准线与对称轴垂直且垂足与焦点关于坐标原点对称;⑤p都是代表焦点到准线的距离(称p为焦参数),∴p>0.?
(2)不同点;对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2,即方程右端一次项的变量与焦点所在坐标轴的名称相同,一次项系数的符号决定抛物线的开口方向.
典型例题:
已知抛物线的标准方程是,求它的焦点坐标和准线方程;
已知抛物线的焦点是,求它的标准方程.
例3、求过点的抛物线的标准方程.
五、当堂检测
1、已知抛物线的标准方程是,求它的焦点坐标和准线方程。
已知抛物线的焦点是,求它的标准方程。
3、根据下列条件写出抛物线的标准方程:
(1)焦点是(2)准线方程是(3)焦点到准线的距离是2
【设计意图:通过三种层次的反馈例练,由浅入深,逐渐达到运用新知的目的,同时反馈学生学习理解的
程度,进行学习监控和补救.】
六、课堂小结
1.知识建构
2.能力提高
3.课堂体验
七、课时练与测
八、教学反思
