北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第24讲《分式与分式方程》全章复习与巩固(基础)(含答案)
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第24讲《分式与分式方程》全章复习与巩固(基础)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-12 00:00:00 | ||
图片预览





文档简介
《分式》全章复习与巩固(基础)
【学习目标】
1. 理解分式的概念,能求出使分式有意义、分式无意义、分式值为0的条件.
2.了解分式的基本性质,掌握分式的约分和通分法则.
3.掌握分式的四则运算.
4.结合分析和解决实际问题,讨论可以化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想.
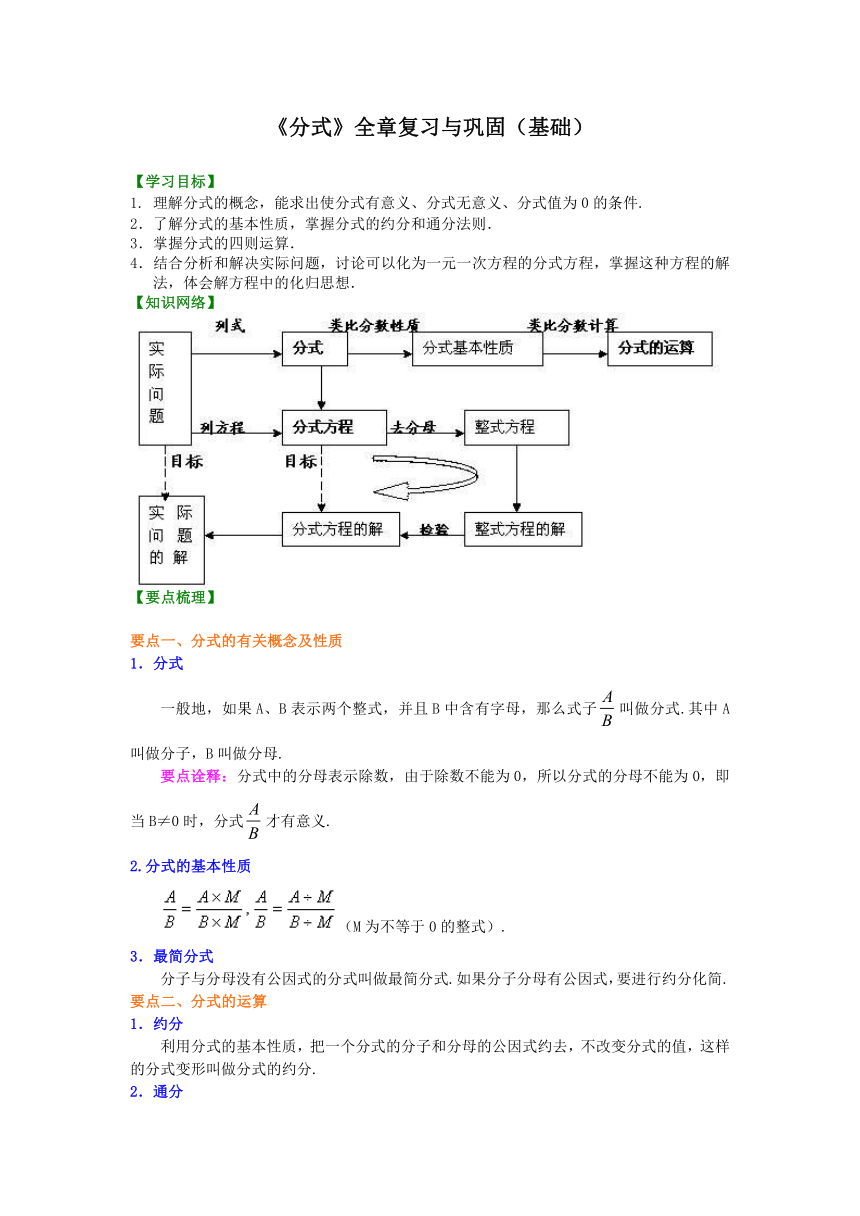
【知识网络】
/【要点梳理】
要点一、分式的有关概念及性质
1.分式
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子/叫做分式.其中A叫做分子,B叫做分母.
要点诠释:分式中的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式/才有意义.
2.分式的基本性质 //(M为不等于0的整式). 3.最简分式
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简.
要点二、分式的运算
1.约分
利用分式的基本性质,把一个分式的分子和分母的公因式约去,不改变分式的值,这样的分式变形叫做分式的约分.
2.通分
利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把异分母的分式化为同分母的分式,这样的分式变形叫做分式的通分.
3.基本运算法则
分式的运算法则与分数的运算法则类似,具体运算法则如下:
(1)加减运算
/ ;同分母的分式相加减,分母不变,把分子相加减.
/ ;异分母的分式相加减,先通分,变为同分母的分式,再加减.
(2)乘法运算 /,其中/是整式,/.
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
(3)除法运算 /,其中/是整式,/.
两个分式相除,把除式的分子和分母颠倒位置后,与被除式相乘.
(4)乘方运算 /
分式的乘方,把分子、分母分别乘方. 4.分式的混合运算顺序
先算乘方,再算乘除,最后加减,有括号先算括号里面的.
要点三、分式方程
1.分式方程的概念
分母中含有未知数的方程叫做分式方程.
2.分式方程的解法
解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程.
3.分式方程的增根问题
增根的产生:分式方程本身隐含着分母不为0的条件,当把分式方程转化为整式方程后,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好使原方程中分母的值为0,那么就会出现不适合原方程的根---增根.
要点诠释:因为解分式方程可能出现增根,所以解分式方程必须验根.验根的方法是将所得的根带入到最简公分母中,看它是否为0,如果为0,即为增根,不为0,就是原方程的解.
要点四、分式方程的应用 列分式方程解应用题与列一元一次方程解应用题类似,但要稍复杂一些.解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,从而正确列出方程,并进行求解.
【典型例题】
类型一、分式及其基本性质
/1、在/中,分式的个数是( )
A.2 B.3 C.4 D.5
【答案】C;
【解析】/是分式.
【总结升华】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
/2、当/为何值时,分式/的值为0?
【思路点拨】先求出使分子为0的字母的值,再检验这个值是否使分母的值等于0,当它使分母的值不等于0时,这个值就是要求的字母的值.
【答案与解析】
解: 要使分式的值为0,必须满足分子等于0且分母不等于0.
由题意,得/ 解得/.
∴ 当/时,分式/的值为0.
【总结升华】分式的值为0的条件是:分子为0,且分母不为0,即只有在分式有意义的前提下,才能考虑分式值的情况.
举一反三:
【变式】(1)若分式/的值等于零,则/=_______; (2)当/________时,分式/没有意义. 【答案】(1)由/=0,得/. 当/=2时/-2=0,所以/=-2; (2)当/,即/=1时,分式/没有意义.
类型二、分式运算
/3、计算:/.
【答案与解析】
解:/
/.
【总结升华】本题有两处易错:一是不按运算顺序运算,把/和/先约分;二是将/和/约分后的结果错认为是1.因此正确掌握运算顺序与符号法则是解题的关键.
举一反三:
【变式】(2019?滨州)化简:/÷(/﹣/)
【答案】
解:原式=/÷/
=/?/
=﹣/.
类型三、分式方程的解法
/4、(2019?呼伦贝尔)解方程:/.
【思路点拨】观察可得最简公分母是(x﹣1)(x+1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【答案与解析】
解:方程的两边同乘(x﹣1)(x+1),得
3x+3﹣x﹣3=0,
解得x=0.
检验:把x=0代入(x﹣1)(x+1)=﹣1≠0.
∴原方程的解为:x=0.
【总结升华】本题考查了分式方程的解法,注:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.
举一反三:
【变式】/,
【答案】
解: 方程两边同乘以/,得
/
检验:当/时,最简公分母/,
∴/是原方程的解.
类型四、分式方程的应用
/5、(2019?东莞二模)某市为治理污水,需要铺设一条全长为600米的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天的工效比原计划增加20%,结果提前5天完成这一任务,原计划每天铺设多少米管道?
【思路点拨】先设原计划每天铺设x米管道,则实际施工时,每天的铺设管道(1+20%)x米,由题意可得等量关系:原计划的工作时间﹣实际的工作时间=5,然后列出方程可求出结果,最后检验并作答.
【答案与解析】
解:设原计划每天铺设x米管道,由题意得:
/﹣/=5,
解得:x=20,
经检验:x=20是原方程的解.
答:原计划每天铺设20米管道.
【总结升华】本题主要考查分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.
举一反三:
【变式】小明家、王老师家、学校在同一条路上,并且小明上学要路过王老师家,小明到王老师家的路程为3 km,王老师家到学校的路程为0.5 km,由于小明的父母战斗在抗震救灾第一线,为了使他能按时到校、王老师每天骑自行车接小明上学.已知王老师骑自行车的速度是他步行速度的3倍,每天比平时步行上班多用了20 min,王老师步行的速度和骑自行车的速度各是多少?
【答案】
解:设王老师步行的速度为/ km/h,则他骑自行车的速度为3/ km/h.
根据题意得:/.
解得:/.
经检验/是原方程的根且符合题意.
当/时,/.
答:王老师步行的速度为5km/h,他骑自行车的速度为15km/h.
【巩固练习】
一.选择题
1.(2019春?无锡期末)下列各式:(﹣m)2,/,/,x2+/y2,5,/,/中,分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.把分式/中的/都扩大3倍,则分式的值( ).
A.扩大3倍 B.扩大6倍
C.缩小为原来的/ D.不变
3.下列各式中,正确的是( ).
A./ B./
C./ D./
4.式子/的值为0,那么/的值是( )
A.2 B.-2 C.±2 D.不存在
5.(2019?德州)化简/﹣/等于( )
A./ B./ C.﹣/ D.﹣/
6.下列分式中,最简分式是( ).
A./ B./
C./ D./
7.将分式方程/化为整式方程时,方程两边应同乘( ).
A./ B./
C./ D./
8.方程/的解是( )
A.0 B.2 C.3 D.无解
二.填空题
9.若x>/,那么/的值是______________.
10.当/______时,分式/有意义.
11.当/______时,分式/的值为正.
12./=______.
13.(2019?内江)化简:(/+/)/= .
14.写出下列分式中的未知的分子或分母:
(1)/;(2)/;(3)/.
15.分式方程/若要化为整式方程,在方程两边同乘的最简公分母是______.
16.方程/的解是______.
三.解答题
17.计算/;(2)/.
18.已知/,求/.
19. 已知/,求/的值.
20.(2019?济南)济南与北京两地相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度是普通快车的3倍,求高铁列车的平均行驶速度.
【答案与解析】
一.选择题
1. 【答案】B;
【解析】解:(﹣m)2,/,x2+/y2,5,/的分母中均不含有字母,因此它们是整式,而不是分式./,/分母中含有字母,因此是分式.
故选B.
2. 【答案】D;
【解析】/.
3. 【答案】A;
【解析】/.
4. 【答案】B;
【解析】由题意/且/,解得/.
5. 【答案】B;
【解析】解:原式=/+/=/+/=/=/,故选B.
6. 【答案】D;
7. 【答案】D;
【解析】原方程的最简公分母为/.
8. 【答案】D;
【解析】解分式方程得/,经检验,/为原方程的增根.
二.填空题
9. 【答案】1;
【解析】若x>/,
不等式两边同时乘以5,得到5x>2,
则2﹣5x<0,
∴|2﹣5x|=5x﹣2,
那么/=/=1..
10.【答案】/;
11.【答案】/;
【解析】要使分式的值为正,需/,解得/.
12.【答案】/;
【解析】/.
13.【答案】a;
【解析】解:原式=/?/=(a+3)?/=a.
14.【答案】(1)/ (2)/ (3)/
15.【答案】/;
16.【答案】/;
【解析】去分母得,/,化简得:/,经检验,/是原方程的根.
三.解答题
17.【解析】
解:(1)/
/
/
/.
(2)原式/.
18.【解析】
解:原式//
/.
当/时,原式/.
19.【解析】
解: 设/,则/,/,/.
所以/.
20.【解析】
解:设普通快车的速度为xkm/时,由题意得:
/﹣/=4,
解得:x=80,
经检验:x=80是原分式方程的解,
3x=3×80=240,
答:高铁列车的平均行驶速度是240km/时.
【学习目标】
1. 理解分式的概念,能求出使分式有意义、分式无意义、分式值为0的条件.
2.了解分式的基本性质,掌握分式的约分和通分法则.
3.掌握分式的四则运算.
4.结合分析和解决实际问题,讨论可以化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想.
【知识网络】
/【要点梳理】
要点一、分式的有关概念及性质
1.分式
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子/叫做分式.其中A叫做分子,B叫做分母.
要点诠释:分式中的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式/才有意义.
2.分式的基本性质 //(M为不等于0的整式). 3.最简分式
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简.
要点二、分式的运算
1.约分
利用分式的基本性质,把一个分式的分子和分母的公因式约去,不改变分式的值,这样的分式变形叫做分式的约分.
2.通分
利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把异分母的分式化为同分母的分式,这样的分式变形叫做分式的通分.
3.基本运算法则
分式的运算法则与分数的运算法则类似,具体运算法则如下:
(1)加减运算
/ ;同分母的分式相加减,分母不变,把分子相加减.
/ ;异分母的分式相加减,先通分,变为同分母的分式,再加减.
(2)乘法运算 /,其中/是整式,/.
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
(3)除法运算 /,其中/是整式,/.
两个分式相除,把除式的分子和分母颠倒位置后,与被除式相乘.
(4)乘方运算 /
分式的乘方,把分子、分母分别乘方. 4.分式的混合运算顺序
先算乘方,再算乘除,最后加减,有括号先算括号里面的.
要点三、分式方程
1.分式方程的概念
分母中含有未知数的方程叫做分式方程.
2.分式方程的解法
解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程.
3.分式方程的增根问题
增根的产生:分式方程本身隐含着分母不为0的条件,当把分式方程转化为整式方程后,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好使原方程中分母的值为0,那么就会出现不适合原方程的根---增根.
要点诠释:因为解分式方程可能出现增根,所以解分式方程必须验根.验根的方法是将所得的根带入到最简公分母中,看它是否为0,如果为0,即为增根,不为0,就是原方程的解.
要点四、分式方程的应用 列分式方程解应用题与列一元一次方程解应用题类似,但要稍复杂一些.解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,从而正确列出方程,并进行求解.
【典型例题】
类型一、分式及其基本性质
/1、在/中,分式的个数是( )
A.2 B.3 C.4 D.5
【答案】C;
【解析】/是分式.
【总结升华】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
/2、当/为何值时,分式/的值为0?
【思路点拨】先求出使分子为0的字母的值,再检验这个值是否使分母的值等于0,当它使分母的值不等于0时,这个值就是要求的字母的值.
【答案与解析】
解: 要使分式的值为0,必须满足分子等于0且分母不等于0.
由题意,得/ 解得/.
∴ 当/时,分式/的值为0.
【总结升华】分式的值为0的条件是:分子为0,且分母不为0,即只有在分式有意义的前提下,才能考虑分式值的情况.
举一反三:
【变式】(1)若分式/的值等于零,则/=_______; (2)当/________时,分式/没有意义. 【答案】(1)由/=0,得/. 当/=2时/-2=0,所以/=-2; (2)当/,即/=1时,分式/没有意义.
类型二、分式运算
/3、计算:/.
【答案与解析】
解:/
/.
【总结升华】本题有两处易错:一是不按运算顺序运算,把/和/先约分;二是将/和/约分后的结果错认为是1.因此正确掌握运算顺序与符号法则是解题的关键.
举一反三:
【变式】(2019?滨州)化简:/÷(/﹣/)
【答案】
解:原式=/÷/
=/?/
=﹣/.
类型三、分式方程的解法
/4、(2019?呼伦贝尔)解方程:/.
【思路点拨】观察可得最简公分母是(x﹣1)(x+1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【答案与解析】
解:方程的两边同乘(x﹣1)(x+1),得
3x+3﹣x﹣3=0,
解得x=0.
检验:把x=0代入(x﹣1)(x+1)=﹣1≠0.
∴原方程的解为:x=0.
【总结升华】本题考查了分式方程的解法,注:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.
举一反三:
【变式】/,
【答案】
解: 方程两边同乘以/,得
/
检验:当/时,最简公分母/,
∴/是原方程的解.
类型四、分式方程的应用
/5、(2019?东莞二模)某市为治理污水,需要铺设一条全长为600米的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天的工效比原计划增加20%,结果提前5天完成这一任务,原计划每天铺设多少米管道?
【思路点拨】先设原计划每天铺设x米管道,则实际施工时,每天的铺设管道(1+20%)x米,由题意可得等量关系:原计划的工作时间﹣实际的工作时间=5,然后列出方程可求出结果,最后检验并作答.
【答案与解析】
解:设原计划每天铺设x米管道,由题意得:
/﹣/=5,
解得:x=20,
经检验:x=20是原方程的解.
答:原计划每天铺设20米管道.
【总结升华】本题主要考查分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.
举一反三:
【变式】小明家、王老师家、学校在同一条路上,并且小明上学要路过王老师家,小明到王老师家的路程为3 km,王老师家到学校的路程为0.5 km,由于小明的父母战斗在抗震救灾第一线,为了使他能按时到校、王老师每天骑自行车接小明上学.已知王老师骑自行车的速度是他步行速度的3倍,每天比平时步行上班多用了20 min,王老师步行的速度和骑自行车的速度各是多少?
【答案】
解:设王老师步行的速度为/ km/h,则他骑自行车的速度为3/ km/h.
根据题意得:/.
解得:/.
经检验/是原方程的根且符合题意.
当/时,/.
答:王老师步行的速度为5km/h,他骑自行车的速度为15km/h.
【巩固练习】
一.选择题
1.(2019春?无锡期末)下列各式:(﹣m)2,/,/,x2+/y2,5,/,/中,分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.把分式/中的/都扩大3倍,则分式的值( ).
A.扩大3倍 B.扩大6倍
C.缩小为原来的/ D.不变
3.下列各式中,正确的是( ).
A./ B./
C./ D./
4.式子/的值为0,那么/的值是( )
A.2 B.-2 C.±2 D.不存在
5.(2019?德州)化简/﹣/等于( )
A./ B./ C.﹣/ D.﹣/
6.下列分式中,最简分式是( ).
A./ B./
C./ D./
7.将分式方程/化为整式方程时,方程两边应同乘( ).
A./ B./
C./ D./
8.方程/的解是( )
A.0 B.2 C.3 D.无解
二.填空题
9.若x>/,那么/的值是______________.
10.当/______时,分式/有意义.
11.当/______时,分式/的值为正.
12./=______.
13.(2019?内江)化简:(/+/)/= .
14.写出下列分式中的未知的分子或分母:
(1)/;(2)/;(3)/.
15.分式方程/若要化为整式方程,在方程两边同乘的最简公分母是______.
16.方程/的解是______.
三.解答题
17.计算/;(2)/.
18.已知/,求/.
19. 已知/,求/的值.
20.(2019?济南)济南与北京两地相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度是普通快车的3倍,求高铁列车的平均行驶速度.
【答案与解析】
一.选择题
1. 【答案】B;
【解析】解:(﹣m)2,/,x2+/y2,5,/的分母中均不含有字母,因此它们是整式,而不是分式./,/分母中含有字母,因此是分式.
故选B.
2. 【答案】D;
【解析】/.
3. 【答案】A;
【解析】/.
4. 【答案】B;
【解析】由题意/且/,解得/.
5. 【答案】B;
【解析】解:原式=/+/=/+/=/=/,故选B.
6. 【答案】D;
7. 【答案】D;
【解析】原方程的最简公分母为/.
8. 【答案】D;
【解析】解分式方程得/,经检验,/为原方程的增根.
二.填空题
9. 【答案】1;
【解析】若x>/,
不等式两边同时乘以5,得到5x>2,
则2﹣5x<0,
∴|2﹣5x|=5x﹣2,
那么/=/=1..
10.【答案】/;
11.【答案】/;
【解析】要使分式的值为正,需/,解得/.
12.【答案】/;
【解析】/.
13.【答案】a;
【解析】解:原式=/?/=(a+3)?/=a.
14.【答案】(1)/ (2)/ (3)/
15.【答案】/;
16.【答案】/;
【解析】去分母得,/,化简得:/,经检验,/是原方程的根.
三.解答题
17.【解析】
解:(1)/
/
/
/.
(2)原式/.
18.【解析】
解:原式//
/.
当/时,原式/.
19.【解析】
解: 设/,则/,/,/.
所以/.
20.【解析】
解:设普通快车的速度为xkm/时,由题意得:
/﹣/=4,
解得:x=80,
经检验:x=80是原分式方程的解,
3x=3×80=240,
答:高铁列车的平均行驶速度是240km/时.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
