高中数学北师大版必修2第一章立体几何初步1.5.2平行关系的性质:21张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.5.2平行关系的性质:21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 663.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 21:51:08 | ||
图片预览







文档简介
课件21张PPT。5.2 平行关系的性质1.能够证明直线与平面平行、平面与平面平行的性质定理.
2.能准确描述并理解线面平行、面面平行的性质定理.
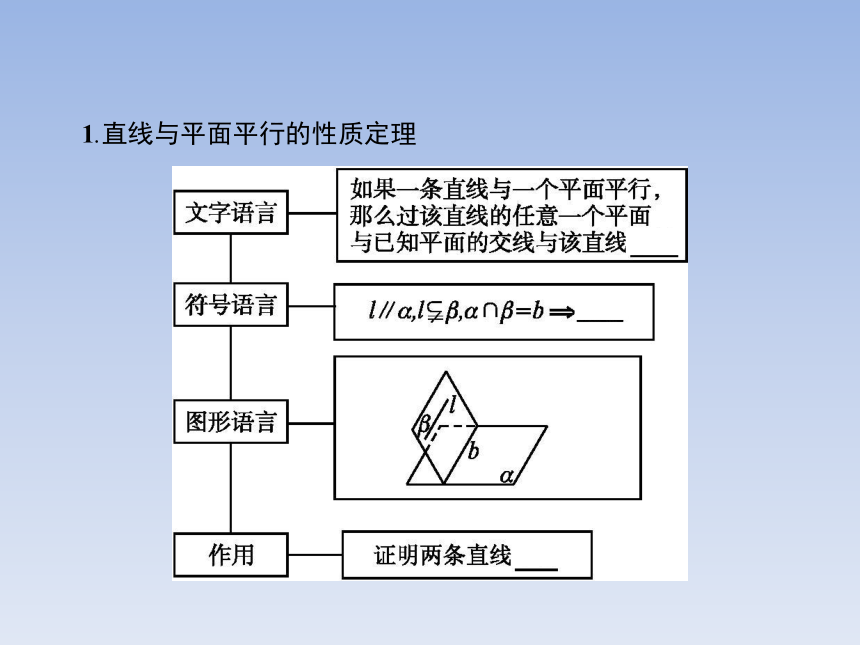
3.能利用两个性质定理解决相关的问题.1.直线与平面平行的性质定理 名师点拨1.直线与平面平行的性质定理可以用来证明直线与直线平行.
2.直线与平面平行的性质定理中有三个条件:(1)直线l和平面α平行,即l∥α;(2)平面α,β相交,即α∩β=b;(3)直线l在平面β内,即l?β.这三个条件缺一不可.【做一做】 如图,ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是 .?
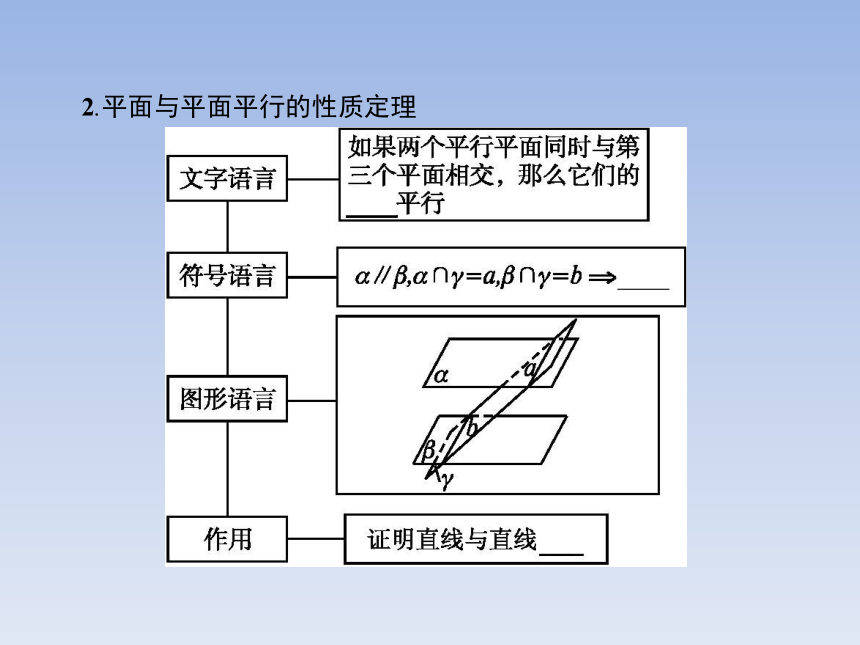
答案:平行2.平面与平面平行的性质定理 题型一题型二题型三【例1】 已知平面α∩平面β=l,直线a∥α,a∥β.
求证:a∥l.
分析:先利用线面平行的性质将线面平行转化为线线平行,再利用平行公理证明.
证明:如图所示,过a作平面γ交平面α于b.
∵a∥α,∴a∥b.
过a作平面δ交平面β于c.
∵a∥β,∴a∥c.∴b∥c.
又b?β,c?β,∴b∥β.
又b?α,α∩β=l,∴b∥l,∴a∥l.题型一题型二题型三题型一题型二题型三【变式训练1】 如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.证明:∵AB∥平面MNPQ,过AB的平面ABC交平面MNPQ于MN,∴AB∥MN.
又过AB的平面ABD交平面MNPQ于PQ,
∴AB∥PQ,∴MN∥PQ.同理可得NP∥MQ.
∴四边形MNPQ为平行四边形.题型一题型二题型三【例2】 如图所示,已知α∥β,P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
分析:由PB与PD相交于点P可知PB,PD确定一个平面,结合α∥β,可使用面面平行的性质定理推出线线平行的关系,这样就转化为平面问题.题型一题型二题型三反思解决已知两个平面平行的问题时,通常用到面面平行的性质.面面平行是平行中的“最高档”,利用面面平行的性质“降低”其档次,即转化为线面平行或线线平行.题型一题型二题型三【变式训练2】 例2中若点P在α与β之间,在第(2)问的条件下,求PD的长.题型一题型二题型三易错点:遗漏题设条件而致误
【例3】 已知直线a,b和平面α,且a∥b,b∥α,a?α.求证:a∥α.
错解:在平面α内任取一点A,过点A作直线c,使c∥b,由a∥b可得a∥c.又a?α,c?α,所以a∥α.
错因分析:上述证明中没有用到条件b∥α,将此条件去掉,结论是不成立的.因而上述“证明”是错误的,错因在于“在α内过任意点A作直线c,使c∥b”,在空间中这样作图是没有依据的.
正解:因为b∥α,设过b的平面与α的交线为d,则b∥d且d?α.
因为a∥b,所以a∥d.
又a?α,d?α,所以a∥α.题型一题型二题型三【变式训练3】 若平面α∥平面β,a?α,b?β,则下列几种说法中一定正确的有 (只填序号).?
(1)a∥b;(2)b与α内的无数条直线平行;(3)b与α内的唯一一条直线平行;(4)a∥β;(5)a与b有可能异面.
答案:(2)(4)(5)1 2 3 4 51.如果一条直线和一个平面平行,那么这条直线( )
A.只和这个平面内的一条直线平行
B.只和这个平面内的两条相交直线不相交
C.和这个平面内的任何一条直线都平行
D.和这个平面内的任何一条直线都不相交
解析:设直线a∥平面α.过a作平面β使α∩β=b,则a∥b,由此可知,平面α内凡是与b平行的直线也都与a平行;凡是与b相交的直线都与a异面,从而可知选项A,B,C均错误,只有选项D正确.
答案:D2.如图所示是长方体被一个平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?
答案:平行四边形1 2 3 4 53.如图所示,直线a∥平面α,点A和直线a分别在α的两侧,点B,C,D∈a.线段AB,AC,AD分别交α于点E,F,G.若BD=4,CF=4,AF=5,则EG= .?1 2 3 4 51 2 3 4 54.如图所示,四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形.求证:四边形ABCD是平行四边形.
证明:∵平面ABCD∥平面α,平面ABCD∩平面AA1B1B=AB,平面AA1B1B∩平面α=A1B1,
∴AB∥A1B1.同理C1D1∥CD.
又四边形A1B1C1D1是平行四边形,
∴A1B1∥C1D1,从而AB∥CD.
同理BC∥AD,故四边形ABCD是平行四边形.1 2 3 4 55.有一块木料如图所示,已知棱BC平行于面A'B'C'D',要经过木料表面A'B'C'D'内的一点P和棱BC将木料锯开,应怎样画线?所画的线和面ABCD有什么关系?1 2 3 4 5 解:∵BC∥平面A'B'C'D',平面BCC'B' 经过BC且和平面A'B'C'D'交于B'C',∴BC∥B'C'.
经过点P,在面A'B'C'D'上画线段EF∥B'C',
根据公理4,EF∥BC.
∴EF?平面BCFE,BC?平面BCFE.
连接BE和CF,则BE,EF,CF就是所要画的线,
如图所示.
由于EF∥BC,根据线面平行的判定定理,得EF∥平面ABCD.
BE,CF显然都和面ABCD相交.1 2 3 4 5
2.能准确描述并理解线面平行、面面平行的性质定理.
3.能利用两个性质定理解决相关的问题.1.直线与平面平行的性质定理 名师点拨1.直线与平面平行的性质定理可以用来证明直线与直线平行.
2.直线与平面平行的性质定理中有三个条件:(1)直线l和平面α平行,即l∥α;(2)平面α,β相交,即α∩β=b;(3)直线l在平面β内,即l?β.这三个条件缺一不可.【做一做】 如图,ABCD-A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是 .?
答案:平行2.平面与平面平行的性质定理 题型一题型二题型三【例1】 已知平面α∩平面β=l,直线a∥α,a∥β.
求证:a∥l.
分析:先利用线面平行的性质将线面平行转化为线线平行,再利用平行公理证明.
证明:如图所示,过a作平面γ交平面α于b.
∵a∥α,∴a∥b.
过a作平面δ交平面β于c.
∵a∥β,∴a∥c.∴b∥c.
又b?β,c?β,∴b∥β.
又b?α,α∩β=l,∴b∥l,∴a∥l.题型一题型二题型三题型一题型二题型三【变式训练1】 如图所示,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.证明:∵AB∥平面MNPQ,过AB的平面ABC交平面MNPQ于MN,∴AB∥MN.
又过AB的平面ABD交平面MNPQ于PQ,
∴AB∥PQ,∴MN∥PQ.同理可得NP∥MQ.
∴四边形MNPQ为平行四边形.题型一题型二题型三【例2】 如图所示,已知α∥β,P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
分析:由PB与PD相交于点P可知PB,PD确定一个平面,结合α∥β,可使用面面平行的性质定理推出线线平行的关系,这样就转化为平面问题.题型一题型二题型三反思解决已知两个平面平行的问题时,通常用到面面平行的性质.面面平行是平行中的“最高档”,利用面面平行的性质“降低”其档次,即转化为线面平行或线线平行.题型一题型二题型三【变式训练2】 例2中若点P在α与β之间,在第(2)问的条件下,求PD的长.题型一题型二题型三易错点:遗漏题设条件而致误
【例3】 已知直线a,b和平面α,且a∥b,b∥α,a?α.求证:a∥α.
错解:在平面α内任取一点A,过点A作直线c,使c∥b,由a∥b可得a∥c.又a?α,c?α,所以a∥α.
错因分析:上述证明中没有用到条件b∥α,将此条件去掉,结论是不成立的.因而上述“证明”是错误的,错因在于“在α内过任意点A作直线c,使c∥b”,在空间中这样作图是没有依据的.
正解:因为b∥α,设过b的平面与α的交线为d,则b∥d且d?α.
因为a∥b,所以a∥d.
又a?α,d?α,所以a∥α.题型一题型二题型三【变式训练3】 若平面α∥平面β,a?α,b?β,则下列几种说法中一定正确的有 (只填序号).?
(1)a∥b;(2)b与α内的无数条直线平行;(3)b与α内的唯一一条直线平行;(4)a∥β;(5)a与b有可能异面.
答案:(2)(4)(5)1 2 3 4 51.如果一条直线和一个平面平行,那么这条直线( )
A.只和这个平面内的一条直线平行
B.只和这个平面内的两条相交直线不相交
C.和这个平面内的任何一条直线都平行
D.和这个平面内的任何一条直线都不相交
解析:设直线a∥平面α.过a作平面β使α∩β=b,则a∥b,由此可知,平面α内凡是与b平行的直线也都与a平行;凡是与b相交的直线都与a异面,从而可知选项A,B,C均错误,只有选项D正确.
答案:D2.如图所示是长方体被一个平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?
答案:平行四边形1 2 3 4 53.如图所示,直线a∥平面α,点A和直线a分别在α的两侧,点B,C,D∈a.线段AB,AC,AD分别交α于点E,F,G.若BD=4,CF=4,AF=5,则EG= .?1 2 3 4 51 2 3 4 54.如图所示,四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形.求证:四边形ABCD是平行四边形.
证明:∵平面ABCD∥平面α,平面ABCD∩平面AA1B1B=AB,平面AA1B1B∩平面α=A1B1,
∴AB∥A1B1.同理C1D1∥CD.
又四边形A1B1C1D1是平行四边形,
∴A1B1∥C1D1,从而AB∥CD.
同理BC∥AD,故四边形ABCD是平行四边形.1 2 3 4 55.有一块木料如图所示,已知棱BC平行于面A'B'C'D',要经过木料表面A'B'C'D'内的一点P和棱BC将木料锯开,应怎样画线?所画的线和面ABCD有什么关系?1 2 3 4 5 解:∵BC∥平面A'B'C'D',平面BCC'B' 经过BC且和平面A'B'C'D'交于B'C',∴BC∥B'C'.
经过点P,在面A'B'C'D'上画线段EF∥B'C',
根据公理4,EF∥BC.
∴EF?平面BCFE,BC?平面BCFE.
连接BE和CF,则BE,EF,CF就是所要画的线,
如图所示.
由于EF∥BC,根据线面平行的判定定理,得EF∥平面ABCD.
BE,CF显然都和面ABCD相交.1 2 3 4 5
