高中数学北师大版必修2第一章立体几何初步1.1.1简单旋转体:28张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.1.1简单旋转体:28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 935.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览





文档简介
课件28张PPT。第一章 立体几何初步§1 简单几何体1.1 简单旋转体1.理解球、圆柱、圆锥、圆台的有关概念,初步掌握运用旋转的观点去观察问题.
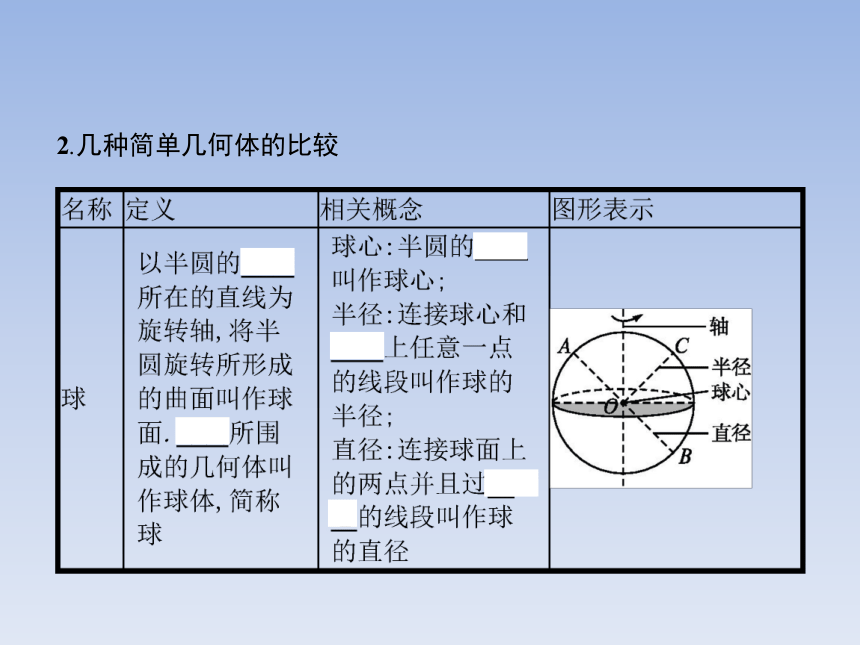
2.理解旋转体的轴截面在几何体中的作用,会利用旋转体的轴截面解决有关计算问题.1.旋转体
(1)概念:一条平面曲线绕着它所在的平面内的一条定
直线旋转所形成的曲面叫作旋转面;封闭的旋转面围成的几何体叫作旋转体.
(2)特殊的旋转体:球、圆柱、圆锥、圆台.
名师点拨如果只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形叫作空间几何体.旋转体是特殊的空间几何体.
【做一做1】 以等腰梯形的对称轴为轴旋转一周,所形成的旋转体为( )
A.圆台 B.圆锥 C.圆柱 D.球
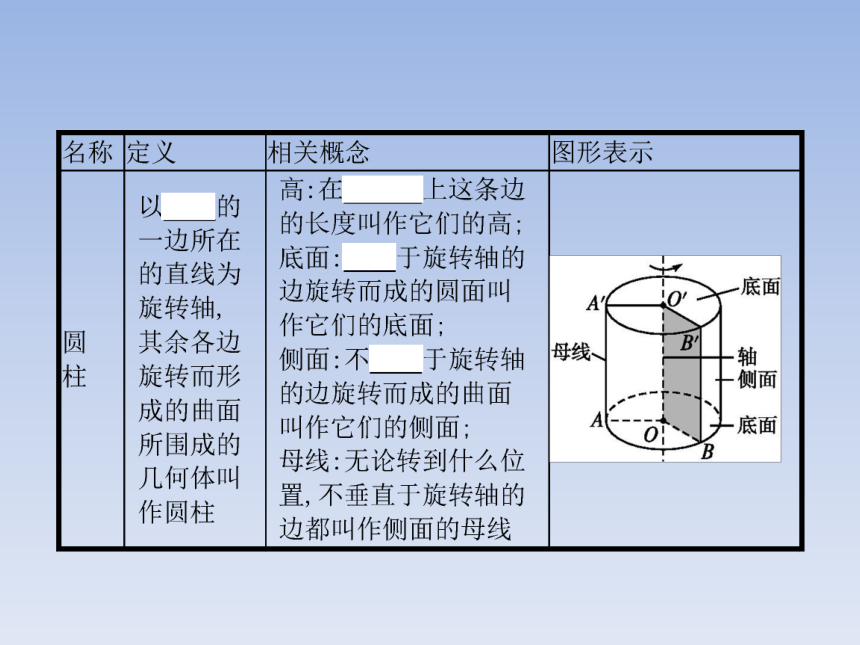
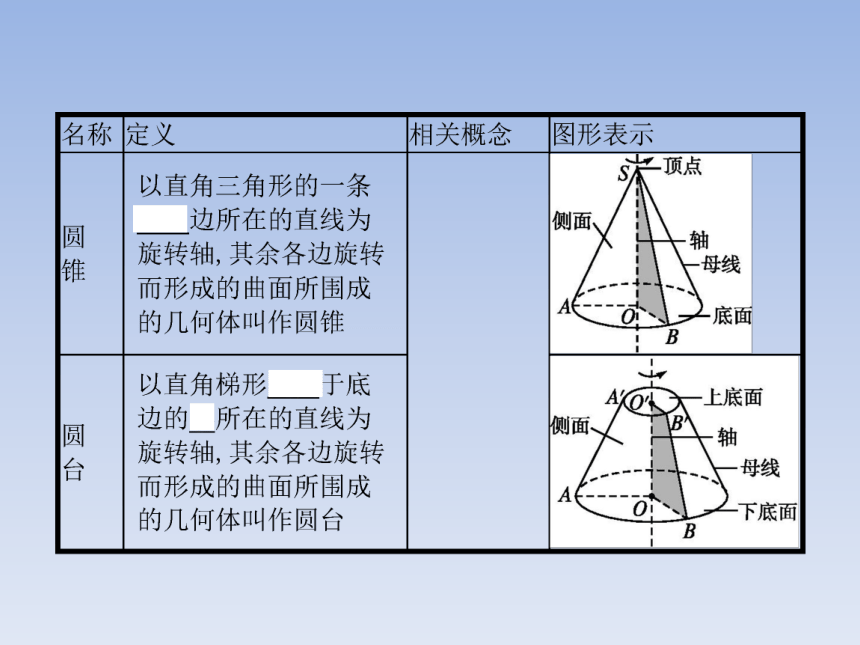
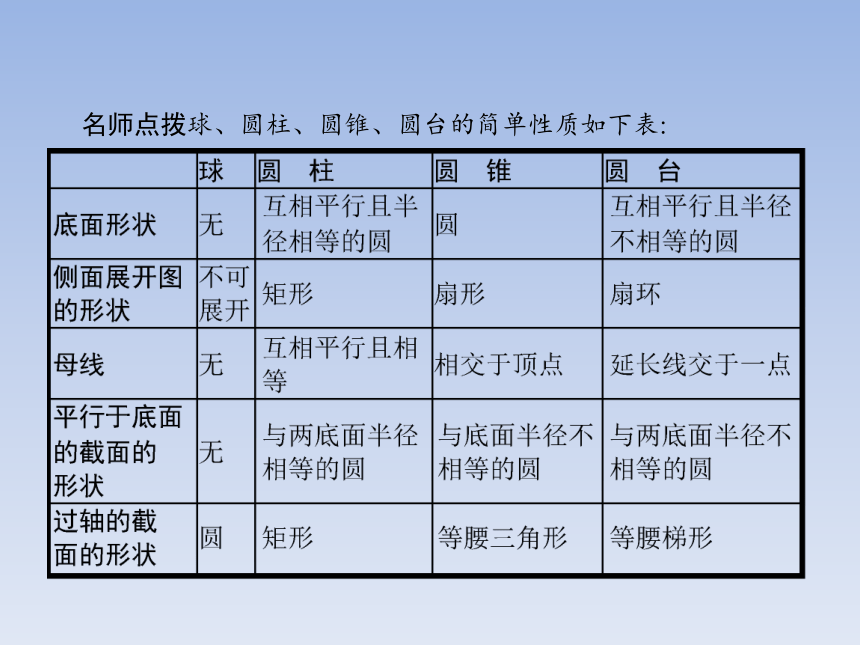
答案:A2.几种简单几何体的比较 名师点拨球、圆柱、圆锥、圆台的简单性质如下表:【做一做2-1】 有下列表述:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是( )
A.①② B.②③ C.①③ D.②④
答案:D【做一做2-2】 有下列说法:
①球的半径是连接球面上任意一点和球心的线段;②球的直径是球面上任意两点间的线段;③用一个平面截一个球,得到的截面的形状是一个圆面;④空间中,到一定点距离相等的点的集合是一个球.
其中正确的有 (只填序号).?
解析:球是半圆绕其直径所在的直线旋转,旋转面所围成的封闭的几何体,不难理解,半圆的直径就是球的直径,半圆的圆心就是球心,半圆的半径就是球的半径,所以①正确;如果球面上的两点连线不经过球心,则这条线段就不是球的直径,所以②错误;球是一个几何体,平面截它应得到一个面而不是一条曲线,所以③正确;空间中到一定点距离相等的点的集合是一个球面,而不是一个球体,所以④错误.
答案:①③题型一题型二题型三题型四【例1】 有下列叙述:
①以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥;
②矩形绕任何一条直线旋转,都可以围成圆柱;
③用一个平面去截圆锥,得到一个圆锥和一个圆台.
其中正确的个数是( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四解析:解答本题可先根据圆柱、圆锥、圆台的结构特征详细分析,再结合已知的各个命题的条件进行具体分析.
以直角三角形的一条直角边所在直线为旋转轴旋转,才可得到圆锥,以直角三角形的斜边所在直线为旋转轴旋转,得到的几何体不是圆锥,故①错误;根据圆柱的定义可知②错误;用平行于圆锥底面的平面去截圆锥,可以得到一个圆锥和一个圆台,用不平行于圆锥底面的平面去截圆锥,不能得到一个圆锥和一个圆台,故③错误.故选A.
答案:A
反思对旋转体定义的理解要准确,认清不同几何体的旋转轴、截面的作用,它们有所不同,判断时要抓住几何体的结构特征,认真分析.题型一题型二题型三题型四【变式训练1】 下列命题中,正确的个数为( )
①圆柱的轴是过圆柱的上、下底面圆的圆心的直线;
②圆柱的母线是连接圆柱上底面上一点和下底面上一点的直线;
③矩形的任意一条边所在直线都可以作为轴,将矩形绕其旋转形成圆柱.
A.0 B.1 C.2 D.3
解析:根据圆柱的定义可知,命题①③正确,命题②错误.故选C.
答案:C题型一题型二题型三题型四【例2】 如图所示,用一个平行于圆锥底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台OO'的母线长.
分析:利用过轴的截面中的两个相似三角形求解.题型一题型二题型三题型四解:设圆台的母线长为l cm,由截得的圆台上、下底面的面积之比为1∶16,可设截得的圆台上、下底面的半径分别为r cm,4r cm.过轴SO作截面,如图所示,题型一题型二题型三题型四反思求解用平行于底面的平面去截圆柱、圆锥、圆台等几何体的相关问题时,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中经过旋转轴的截面(轴截面)的性质,建立相关几何变量的方程(组),然后解方程(组).题型一题型二题型三题型四【变式训练2】 有一个半径为5的半圆,将它卷成一个圆锥的侧面,求圆锥的高.题型一题型二题型三题型四【例3】 用一个平面截半径为5 cm的球,球心到截面的距离为4 cm,求截面圆的面积.
解:如图所示,设AK为截面圆的半径,则OK⊥AK.
在Rt△OAK中,OA=5 cm,OK=4 cm,
∴截面圆的面积为π·AK2=9π(cm2).
反思对于球的性质,要着重掌握其截面性质:(1)用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.(2)如果分别用R和r表示球的半径和截面圆的半径,用d表示球心到截面的距离,则R2=r2+d2.题型一题型二题型三题型四【变式训练3】 在半径为25 cm的球内有一个截面,它的面积是49π cm2,则球心到这个截面的距离是 .?
解析:球的截面是一个圆面,已知截面面积可以求得截面的半径,然后利用球心到截面的距离、截面圆的半径和球的半径之间的关系可求得球心到截面的距离.
于是设球的半径为R,截面圆的半径为r,
球心到截面的距离为d,如图所示.
∵S=πr2=49π(cm2),∴r=7 cm.
∴球心到这个截面的距离为24 cm.
答案:24 cm题型一题型二题型三题型四易错点:对旋转体的概念认识不清而致误
【例4】 给出下列结论:①一个圆绕其一条直径所在的直线旋转180°形成的封闭曲面围成的几何体是圆面;②圆锥的母线长等于底面圆的直径;③平行于圆锥的一条母线的截面是等腰三角形;④圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线.
其中正确的是 .?
错解:①②③④
错因分析:错选①是对球的概念理解不透彻而致误;错选②③是对圆锥的概念认识不到位而导致判断失误.结合旋转体的图形,正确理解其概念的内涵和外延,把握好它们的结构特征是解这类题的关键.题型一题型二题型三题型四正解:①错,该几何体是球;②错,圆锥的母线长与底面圆的直径无直接关系;③错,平行于圆锥一条母线的截面不是多边形,因为它的边界有曲线段,只有过母线且过顶点作截面才会出现等腰三角形.由圆锥母线的定义知④正确.
答案:④题型一题型二题型三题型四【变式训练4】 下列说法正确的是 .(只填序号)?
①夹在圆柱的两个平行截面间的几何体还是一个旋转体;②圆柱的底面是圆;③连接圆柱上、下底面圆周上两点的线段是母线;④圆锥中过轴的截面是全等的等腰三角形.
解析:①错,当两个截面不平行于上、下两个底面时,两个截面间的几何体不是旋转体;②错,圆柱的底面是圆面而不是圆;③错,连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行,所以不一定是圆柱的母线;④正确.
答案:④1 2 3 41.圆台的所有母线的位置关系是( )
A.平行 B.在同一平面内
C.延长后交于一点 D.垂直
答案:C1 2 3 42一个底面直径等于高的圆柱的轴截面面积是S,则它的一个底面面积是( )
答案:B1 2 3 43.有以下说法:
①以直角梯形的一条边所在直线为旋转轴,旋转所成的几何体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③分别以矩形两条不同的边所在直线为旋转轴,将矩形旋转一周,所得的两个圆柱可能是两个不同的圆柱.
其中正确的个数为( )
A.0 B.1
C.2 D.3
解析:①中若以直角梯形中不垂直于上下底边的腰为轴旋转所得几何体就不是圆台,②中各旋转体的底面是圆面不是圆,③是正确的.
答案:B1 2 3 44.一个圆台的母线长为12 cm,两底面的面积分别为4π cm2和25π cm2.求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.1 2 3 4
2.理解旋转体的轴截面在几何体中的作用,会利用旋转体的轴截面解决有关计算问题.1.旋转体
(1)概念:一条平面曲线绕着它所在的平面内的一条定
直线旋转所形成的曲面叫作旋转面;封闭的旋转面围成的几何体叫作旋转体.
(2)特殊的旋转体:球、圆柱、圆锥、圆台.
名师点拨如果只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形叫作空间几何体.旋转体是特殊的空间几何体.
【做一做1】 以等腰梯形的对称轴为轴旋转一周,所形成的旋转体为( )
A.圆台 B.圆锥 C.圆柱 D.球
答案:A2.几种简单几何体的比较 名师点拨球、圆柱、圆锥、圆台的简单性质如下表:【做一做2-1】 有下列表述:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是( )
A.①② B.②③ C.①③ D.②④
答案:D【做一做2-2】 有下列说法:
①球的半径是连接球面上任意一点和球心的线段;②球的直径是球面上任意两点间的线段;③用一个平面截一个球,得到的截面的形状是一个圆面;④空间中,到一定点距离相等的点的集合是一个球.
其中正确的有 (只填序号).?
解析:球是半圆绕其直径所在的直线旋转,旋转面所围成的封闭的几何体,不难理解,半圆的直径就是球的直径,半圆的圆心就是球心,半圆的半径就是球的半径,所以①正确;如果球面上的两点连线不经过球心,则这条线段就不是球的直径,所以②错误;球是一个几何体,平面截它应得到一个面而不是一条曲线,所以③正确;空间中到一定点距离相等的点的集合是一个球面,而不是一个球体,所以④错误.
答案:①③题型一题型二题型三题型四【例1】 有下列叙述:
①以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥;
②矩形绕任何一条直线旋转,都可以围成圆柱;
③用一个平面去截圆锥,得到一个圆锥和一个圆台.
其中正确的个数是( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四解析:解答本题可先根据圆柱、圆锥、圆台的结构特征详细分析,再结合已知的各个命题的条件进行具体分析.
以直角三角形的一条直角边所在直线为旋转轴旋转,才可得到圆锥,以直角三角形的斜边所在直线为旋转轴旋转,得到的几何体不是圆锥,故①错误;根据圆柱的定义可知②错误;用平行于圆锥底面的平面去截圆锥,可以得到一个圆锥和一个圆台,用不平行于圆锥底面的平面去截圆锥,不能得到一个圆锥和一个圆台,故③错误.故选A.
答案:A
反思对旋转体定义的理解要准确,认清不同几何体的旋转轴、截面的作用,它们有所不同,判断时要抓住几何体的结构特征,认真分析.题型一题型二题型三题型四【变式训练1】 下列命题中,正确的个数为( )
①圆柱的轴是过圆柱的上、下底面圆的圆心的直线;
②圆柱的母线是连接圆柱上底面上一点和下底面上一点的直线;
③矩形的任意一条边所在直线都可以作为轴,将矩形绕其旋转形成圆柱.
A.0 B.1 C.2 D.3
解析:根据圆柱的定义可知,命题①③正确,命题②错误.故选C.
答案:C题型一题型二题型三题型四【例2】 如图所示,用一个平行于圆锥底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台OO'的母线长.
分析:利用过轴的截面中的两个相似三角形求解.题型一题型二题型三题型四解:设圆台的母线长为l cm,由截得的圆台上、下底面的面积之比为1∶16,可设截得的圆台上、下底面的半径分别为r cm,4r cm.过轴SO作截面,如图所示,题型一题型二题型三题型四反思求解用平行于底面的平面去截圆柱、圆锥、圆台等几何体的相关问题时,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中经过旋转轴的截面(轴截面)的性质,建立相关几何变量的方程(组),然后解方程(组).题型一题型二题型三题型四【变式训练2】 有一个半径为5的半圆,将它卷成一个圆锥的侧面,求圆锥的高.题型一题型二题型三题型四【例3】 用一个平面截半径为5 cm的球,球心到截面的距离为4 cm,求截面圆的面积.
解:如图所示,设AK为截面圆的半径,则OK⊥AK.
在Rt△OAK中,OA=5 cm,OK=4 cm,
∴截面圆的面积为π·AK2=9π(cm2).
反思对于球的性质,要着重掌握其截面性质:(1)用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.(2)如果分别用R和r表示球的半径和截面圆的半径,用d表示球心到截面的距离,则R2=r2+d2.题型一题型二题型三题型四【变式训练3】 在半径为25 cm的球内有一个截面,它的面积是49π cm2,则球心到这个截面的距离是 .?
解析:球的截面是一个圆面,已知截面面积可以求得截面的半径,然后利用球心到截面的距离、截面圆的半径和球的半径之间的关系可求得球心到截面的距离.
于是设球的半径为R,截面圆的半径为r,
球心到截面的距离为d,如图所示.
∵S=πr2=49π(cm2),∴r=7 cm.
∴球心到这个截面的距离为24 cm.
答案:24 cm题型一题型二题型三题型四易错点:对旋转体的概念认识不清而致误
【例4】 给出下列结论:①一个圆绕其一条直径所在的直线旋转180°形成的封闭曲面围成的几何体是圆面;②圆锥的母线长等于底面圆的直径;③平行于圆锥的一条母线的截面是等腰三角形;④圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线.
其中正确的是 .?
错解:①②③④
错因分析:错选①是对球的概念理解不透彻而致误;错选②③是对圆锥的概念认识不到位而导致判断失误.结合旋转体的图形,正确理解其概念的内涵和外延,把握好它们的结构特征是解这类题的关键.题型一题型二题型三题型四正解:①错,该几何体是球;②错,圆锥的母线长与底面圆的直径无直接关系;③错,平行于圆锥一条母线的截面不是多边形,因为它的边界有曲线段,只有过母线且过顶点作截面才会出现等腰三角形.由圆锥母线的定义知④正确.
答案:④题型一题型二题型三题型四【变式训练4】 下列说法正确的是 .(只填序号)?
①夹在圆柱的两个平行截面间的几何体还是一个旋转体;②圆柱的底面是圆;③连接圆柱上、下底面圆周上两点的线段是母线;④圆锥中过轴的截面是全等的等腰三角形.
解析:①错,当两个截面不平行于上、下两个底面时,两个截面间的几何体不是旋转体;②错,圆柱的底面是圆面而不是圆;③错,连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行,所以不一定是圆柱的母线;④正确.
答案:④1 2 3 41.圆台的所有母线的位置关系是( )
A.平行 B.在同一平面内
C.延长后交于一点 D.垂直
答案:C1 2 3 42一个底面直径等于高的圆柱的轴截面面积是S,则它的一个底面面积是( )
答案:B1 2 3 43.有以下说法:
①以直角梯形的一条边所在直线为旋转轴,旋转所成的几何体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③分别以矩形两条不同的边所在直线为旋转轴,将矩形旋转一周,所得的两个圆柱可能是两个不同的圆柱.
其中正确的个数为( )
A.0 B.1
C.2 D.3
解析:①中若以直角梯形中不垂直于上下底边的腰为轴旋转所得几何体就不是圆台,②中各旋转体的底面是圆面不是圆,③是正确的.
答案:B1 2 3 44.一个圆台的母线长为12 cm,两底面的面积分别为4π cm2和25π cm2.求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.1 2 3 4
