高中数学北师大版必修2第一章立体几何初步1.1.2简单多面体:31张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.1.2简单多面体:31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 765.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览







文档简介
课件31张PPT。1.2 简单多面体1.知道多面体、棱柱、棱锥、棱台的结构特征,并能结合这些结构特征认识常见几何体.
2.掌握棱锥、棱台平行于底面的截面的性质.
3.知道棱柱、棱锥、棱台的分类及表示方法,认识正棱柱、正棱锥、正棱台的结构特征及性质.1.多面体
(1)概念:若干个平面多边形围成的几何体叫作多面体.
(2)棱柱、棱锥、棱台是简单多面体.
围成多面体的各个多边形叫作多面体的面;相邻两个面的公共边叫作多面体的棱;棱与棱的公共点叫作多面体的顶点.2.棱柱
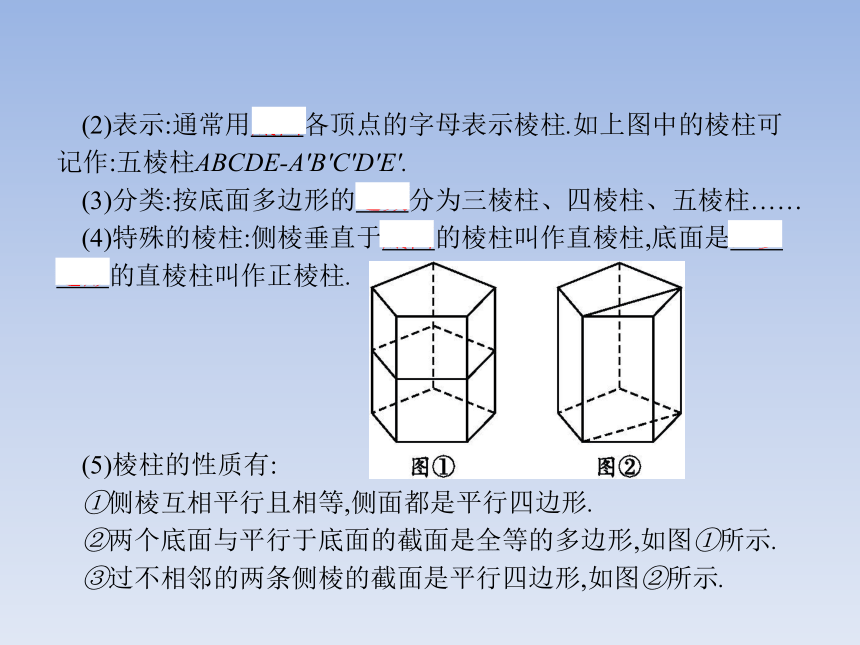
(1)概念:两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱.这里两个互相平行的面叫作棱柱的底面,其余各面叫作棱柱的侧面;两个面的公共边叫作棱柱的棱,其中两个侧面的公共边叫作棱柱的侧棱,底面多边形与侧面的公共顶点叫作棱柱的顶点.如图所示.(2)表示:通常用底面各顶点的字母表示棱柱.如上图中的棱柱可记作:五棱柱ABCDE-A'B'C'D'E'.
(3)分类:按底面多边形的边数分为三棱柱、四棱柱、五棱柱……
(4)特殊的棱柱:侧棱垂直于底面的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱.
(5)棱柱的性质有:
①侧棱互相平行且相等,侧面都是平行四边形.
②两个底面与平行于底面的截面是全等的多边形,如图①所示.
③过不相邻的两条侧棱的截面是平行四边形,如图②所示.名师点拨四棱柱是一种常见的棱柱,它的侧棱与底面的变化会产生一系列特殊的四棱柱.【做一做1-1】 棱柱的侧面不可能是( )
A.三角形 B.平行四边形 C.矩形 D.正方形
答案:A
【做一做1-2】 一个棱柱至少有 个面, 个顶点, 条棱.?
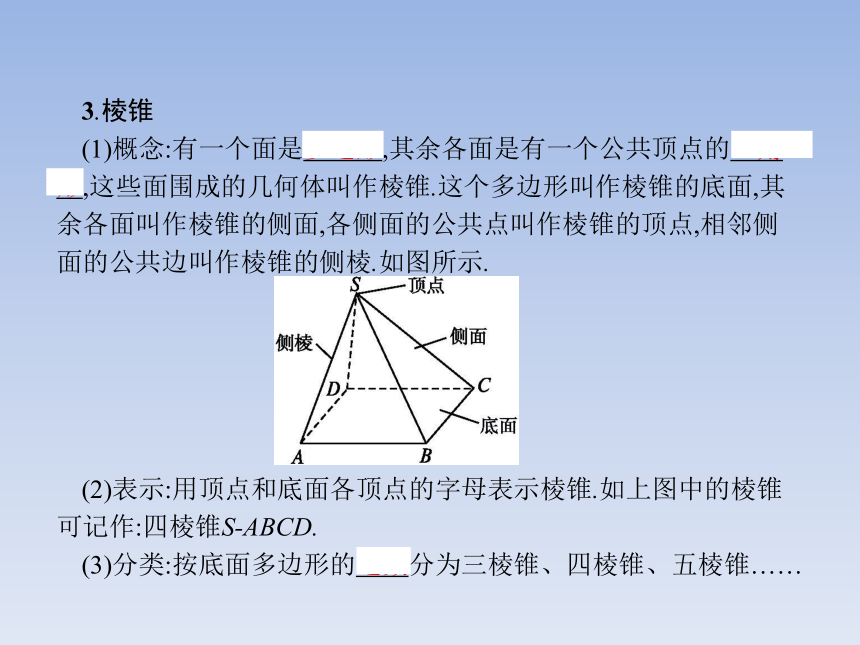
答案:5 6 93.棱锥
(1)概念:有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.这个多边形叫作棱锥的底面,其余各面叫作棱锥的侧面,各侧面的公共点叫作棱锥的顶点,相邻侧面的公共边叫作棱锥的侧棱.如图所示.
(2)表示:用顶点和底面各顶点的字母表示棱锥.如上图中的棱锥可记作:四棱锥S-ABCD.
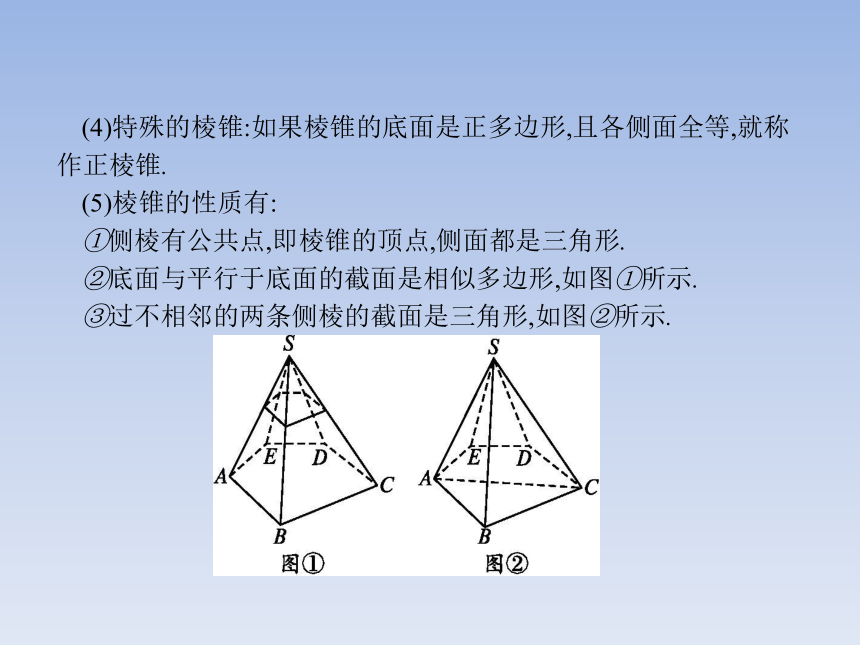
(3)分类:按底面多边形的边数分为三棱锥、四棱锥、五棱锥……(4)特殊的棱锥:如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥.
(5)棱锥的性质有:
①侧棱有公共点,即棱锥的顶点,侧面都是三角形.
②底面与平行于底面的截面是相似多边形,如图①所示.
③过不相邻的两条侧棱的截面是三角形,如图②所示.【做一做2】 在正方形ABCD中,E,F分别为BC,CD的中点,沿AE,AF,EF将其折成一个多面体,则此多面体是 .?
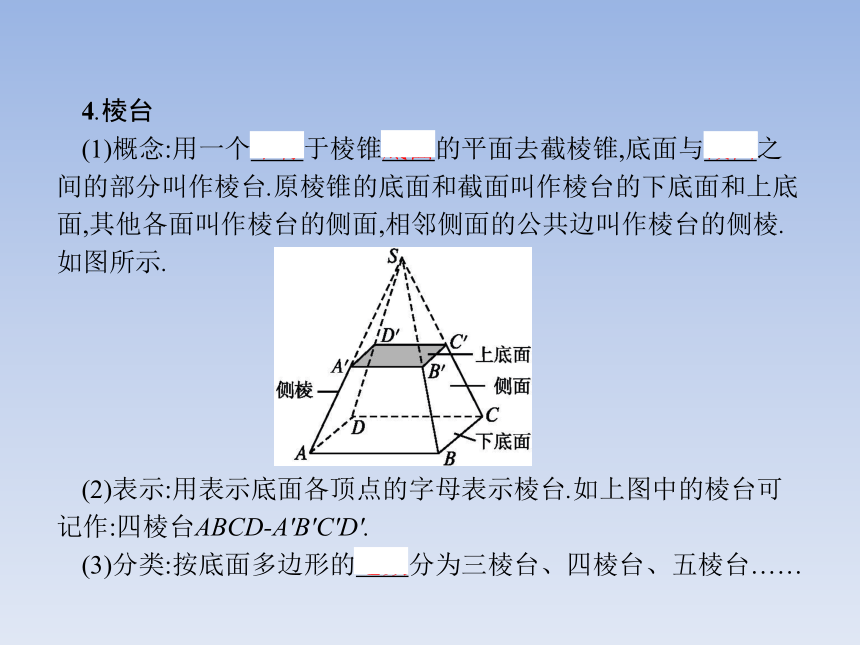
答案:三棱锥4.棱台
(1)概念:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的侧棱.如图所示.
(2)表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记作:四棱台ABCD-A'B'C'D'.
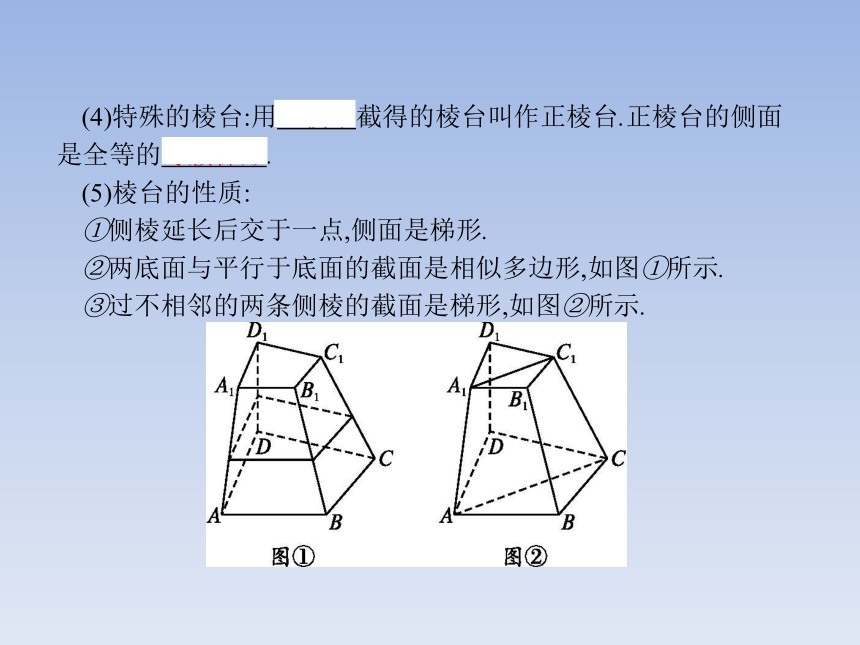
(3)分类:按底面多边形的边数分为三棱台、四棱台、五棱台……(4)特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是全等的等腰梯形.
(5)棱台的性质:
①侧棱延长后交于一点,侧面是梯形.
②两底面与平行于底面的截面是相似多边形,如图①所示.
③过不相邻的两条侧棱的截面是梯形,如图②所示.【做一做3】 三棱台的三条侧棱( )
A.互相平行 B.延长后交于一点
C.互相垂直 D.相等
答案:B题型一题型二题型三题型四【例1】 如图所示,已知长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,判断是几棱柱并找出棱柱的底面;如果不是,请说明理由.
分析:利用棱柱的定义进行判断.题型一题型二题型三题型四解:(1)是棱柱,且是四棱柱.因为以长方体相对的两个面作为底面,它们互相平行且都是四边形,其余各面都是矩形,当然是平行四边形,并且四条侧棱互相平行,符合棱柱的概念.
(2)截面BCFE右上方部分是棱柱,且是三棱柱,其中△BEB1和△CFC1是底面.
截面BCFE左下方部分也是棱柱,且是四棱柱,其中四边形ABEA1和四边形DCFD1是底面.
反思对于棱柱,不要只认为底面就是在上下位置,也可以在前后位置或左右位置.题型一题型二题型三题型四【变式训练1】 下列命题中,正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫作棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形解析:A选项漏掉了侧棱平行的特点;对于B选项,如图所示,构造四棱柱ABCD-A1B1C1D1,令四边形ABCD是梯形,可知平面ABB1A1∥平面DCC1D1,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形;D选项说明了棱柱的特点,故选D.
答案:D题型一题型二题型三题型四【例2】 给出下列结论:
①棱锥的侧面为三角形,且所有的侧面都有一个公共顶点;
②多面体至少有四个面;
③棱台的侧棱所在直线均相交于同一点.
其中,错误的个数是( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四解析:①显然是正确的;
对于②,显然一个图形要成为空间几何体,它至少需有四个顶点,因为三个顶点只围成一个三角形,当有四个顶点时,易知它可以围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故②是正确的;
对于③,棱台的侧棱所在的直线就是原棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,即棱锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故③是正确的.
答案:A
反思只有理解并掌握好各种简单多面体的概念及相应的结构特征,才能对问题作出正确的判断.题型一题型二题型三题型四【变式训练2】 有下列四个命题:①棱台的上、下底面多边形是相似的;②用一个平面去截棱锥,夹在底面和截面间的几何体是棱台;③棱台的上、下底面边长之比等于棱台的高与截得此棱台的棱锥的高的比;④两个底面平行且相似,其余各面是梯形的几何体是棱台.其中正确的命题有 (填写所有正确命题的序号).?解析:根据棱台的定义和结构特征知①正确;②中截面不一定平行于底面,所得几何体不一定是棱台,故②不正确;棱台的上、下底面边长的比等于被截去的小棱锥与原棱锥的高之比,故③不正确;如图所示,AA1,BB1,CC1,DD1延长后没有交于同一点,故④不正确.
答案:①题型一题型二题型三题型四【例3】 已知,在正三棱锥V-ABC中,底面边长为8,侧棱长为2 ,计算它的高和斜高.
分析本题主要考查正三棱锥中基本量的计算,关键是把已知量与未知量放到直角三角形中求解.题型一题型二题型三题型四解如图所示,设O是底面中心,连接AO并延长,交BC于点D,则D为BC的中点,∴△VAO和△VCD都是直角三角形.题型一题型二题型三题型四反思正棱锥中基本量的计算要借助构造的直角三角形.一般包括高、斜高和底面内切圆半径组成的直角三角形;高、侧棱和底面外接圆半径组成的直角三角形;斜高、侧棱和底面边长的一半组成的直角三角形.
类似地,在正棱台中,有三个重要的直角梯形:两底面中心连线、相应的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和相应两底面正多边形的顶点与中心连线组成一个直角梯形;斜高、侧棱和上、下两底面边长的一半组成一个直角梯形.正棱台的计算问题,实际上就是这几个直角梯形的计算问题.题型一题型二题型三题型四【变式训练3】 一个正四棱台的高是17 cm,上、下底面边长分别为4 cm和16 cm.求这个棱台的侧棱长和斜高.
解:如图所示,取上、下底面的中心O1,O,B1C1和BC的中点E1,E.
连接O1O,OE,EE1,O1E1,OB,O1B1.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,题型一题型二题型三题型四易错点:对概念理解不清而致误
【例4】 下列关于棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
②若过相对棱的两个截面都垂直于底面,则该四棱柱为直四棱柱;
③若侧面两两全等,则该四棱柱为直四棱柱;
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.
其中,真命题的序号是 .?
错解:①②④
错因分析:①中必须是两个相邻的侧面,对概念理解不透彻而误认为①也是正确的.题型一题型二题型三题型四正解:①错,必须是两个相邻的侧面;②正确;③错误,反例:斜四棱柱;④正确,对角线两两相等,则此对角线组成的平行四边形为矩形,故填②④.
答案:②④题型一题型二题型三题型四【变式训练4】 下列命题中:
①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;
②有一个面是多边形,其余各面都是三角形所围成的几何体是棱锥;
③用一个平行于棱锥底面的平面截棱锥,得到的几何体是棱台.
真命题的个数是( )
A.0 B.1 C.2 D.3
解析:命题①②不符合棱柱及棱锥的定义,命题③,用一个平行于棱锥底面的平面去截棱锥,得到的几何体一个是棱台,另一个是棱锥,故③错误.
答案:A1 2 3 4 51.正五棱柱中,若不同在任一侧面且不同在任一底面的两顶点的连线称为它的对角线,则一个正五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
解析:方法一:在上底面选一个点,同时在下底面选一个点,且这两个点不在同一侧面上,这样上底面每个点对应2条对角线,所以共有10条.方法二:过正五棱柱任意不相邻的两条侧棱可得一个截面,每个截面可得到正五棱柱的两条对角线,5个截面共可得到10条对角线.
答案:D1 2 3 4 52.下列说法错误的是( )
A.多面体至少有四个面
B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
解析:多面体中面数最少的是三棱锥,有四个面,故A正确.根据棱柱的结构特征知B正确.长方体、正方体符合棱柱的结构特征,C正确.D中三棱柱的侧面为平行四边形,D错误.
答案:D1 2 3 4 53.如图所示,下列几何体中, 是棱柱, 是棱锥, 是棱台.?
解析:由棱柱、棱锥、棱台的定义知,①②③④符合棱柱的定义;⑥符合棱锥的定义;⑤符合棱台的定义.
答案:①②③④ ⑥ ⑤1 2 3 4 54.说出四棱台有多少个顶点?多少条棱?多少个面?四棱锥呢?
解:作四棱锥P-ABCD,用平行于底面ABCD的平面A1B1C1D1截该棱锥得四棱台ABCD-A1B1C1D1,如图所示,由图得四棱台有8个顶点,12条棱,6个面;四棱锥有5个顶点,8条棱,5个面.1 2 3 4 55.
如图所示,已知该几何体所有的棱长都相等,试分析此几何体的面数、顶点数和棱数,并判断该几何体是不是棱柱、棱锥、棱台的一种.
解:该几何体有8个面,6个顶点,12条棱,它不满足棱柱、棱锥、棱台的定义,故不是棱柱,也不是棱锥,也不是棱台,但它是一个多面体.
2.掌握棱锥、棱台平行于底面的截面的性质.
3.知道棱柱、棱锥、棱台的分类及表示方法,认识正棱柱、正棱锥、正棱台的结构特征及性质.1.多面体
(1)概念:若干个平面多边形围成的几何体叫作多面体.
(2)棱柱、棱锥、棱台是简单多面体.
围成多面体的各个多边形叫作多面体的面;相邻两个面的公共边叫作多面体的棱;棱与棱的公共点叫作多面体的顶点.2.棱柱
(1)概念:两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱.这里两个互相平行的面叫作棱柱的底面,其余各面叫作棱柱的侧面;两个面的公共边叫作棱柱的棱,其中两个侧面的公共边叫作棱柱的侧棱,底面多边形与侧面的公共顶点叫作棱柱的顶点.如图所示.(2)表示:通常用底面各顶点的字母表示棱柱.如上图中的棱柱可记作:五棱柱ABCDE-A'B'C'D'E'.
(3)分类:按底面多边形的边数分为三棱柱、四棱柱、五棱柱……
(4)特殊的棱柱:侧棱垂直于底面的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱.
(5)棱柱的性质有:
①侧棱互相平行且相等,侧面都是平行四边形.
②两个底面与平行于底面的截面是全等的多边形,如图①所示.
③过不相邻的两条侧棱的截面是平行四边形,如图②所示.名师点拨四棱柱是一种常见的棱柱,它的侧棱与底面的变化会产生一系列特殊的四棱柱.【做一做1-1】 棱柱的侧面不可能是( )
A.三角形 B.平行四边形 C.矩形 D.正方形
答案:A
【做一做1-2】 一个棱柱至少有 个面, 个顶点, 条棱.?
答案:5 6 93.棱锥
(1)概念:有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.这个多边形叫作棱锥的底面,其余各面叫作棱锥的侧面,各侧面的公共点叫作棱锥的顶点,相邻侧面的公共边叫作棱锥的侧棱.如图所示.
(2)表示:用顶点和底面各顶点的字母表示棱锥.如上图中的棱锥可记作:四棱锥S-ABCD.
(3)分类:按底面多边形的边数分为三棱锥、四棱锥、五棱锥……(4)特殊的棱锥:如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥.
(5)棱锥的性质有:
①侧棱有公共点,即棱锥的顶点,侧面都是三角形.
②底面与平行于底面的截面是相似多边形,如图①所示.
③过不相邻的两条侧棱的截面是三角形,如图②所示.【做一做2】 在正方形ABCD中,E,F分别为BC,CD的中点,沿AE,AF,EF将其折成一个多面体,则此多面体是 .?
答案:三棱锥4.棱台
(1)概念:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的侧棱.如图所示.
(2)表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记作:四棱台ABCD-A'B'C'D'.
(3)分类:按底面多边形的边数分为三棱台、四棱台、五棱台……(4)特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是全等的等腰梯形.
(5)棱台的性质:
①侧棱延长后交于一点,侧面是梯形.
②两底面与平行于底面的截面是相似多边形,如图①所示.
③过不相邻的两条侧棱的截面是梯形,如图②所示.【做一做3】 三棱台的三条侧棱( )
A.互相平行 B.延长后交于一点
C.互相垂直 D.相等
答案:B题型一题型二题型三题型四【例1】 如图所示,已知长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCFE把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,判断是几棱柱并找出棱柱的底面;如果不是,请说明理由.
分析:利用棱柱的定义进行判断.题型一题型二题型三题型四解:(1)是棱柱,且是四棱柱.因为以长方体相对的两个面作为底面,它们互相平行且都是四边形,其余各面都是矩形,当然是平行四边形,并且四条侧棱互相平行,符合棱柱的概念.
(2)截面BCFE右上方部分是棱柱,且是三棱柱,其中△BEB1和△CFC1是底面.
截面BCFE左下方部分也是棱柱,且是四棱柱,其中四边形ABEA1和四边形DCFD1是底面.
反思对于棱柱,不要只认为底面就是在上下位置,也可以在前后位置或左右位置.题型一题型二题型三题型四【变式训练1】 下列命题中,正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫作棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形解析:A选项漏掉了侧棱平行的特点;对于B选项,如图所示,构造四棱柱ABCD-A1B1C1D1,令四边形ABCD是梯形,可知平面ABB1A1∥平面DCC1D1,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形;D选项说明了棱柱的特点,故选D.
答案:D题型一题型二题型三题型四【例2】 给出下列结论:
①棱锥的侧面为三角形,且所有的侧面都有一个公共顶点;
②多面体至少有四个面;
③棱台的侧棱所在直线均相交于同一点.
其中,错误的个数是( )
A.0 B.1 C.2 D.3题型一题型二题型三题型四解析:①显然是正确的;
对于②,显然一个图形要成为空间几何体,它至少需有四个顶点,因为三个顶点只围成一个三角形,当有四个顶点时,易知它可以围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故②是正确的;
对于③,棱台的侧棱所在的直线就是原棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,即棱锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故③是正确的.
答案:A
反思只有理解并掌握好各种简单多面体的概念及相应的结构特征,才能对问题作出正确的判断.题型一题型二题型三题型四【变式训练2】 有下列四个命题:①棱台的上、下底面多边形是相似的;②用一个平面去截棱锥,夹在底面和截面间的几何体是棱台;③棱台的上、下底面边长之比等于棱台的高与截得此棱台的棱锥的高的比;④两个底面平行且相似,其余各面是梯形的几何体是棱台.其中正确的命题有 (填写所有正确命题的序号).?解析:根据棱台的定义和结构特征知①正确;②中截面不一定平行于底面,所得几何体不一定是棱台,故②不正确;棱台的上、下底面边长的比等于被截去的小棱锥与原棱锥的高之比,故③不正确;如图所示,AA1,BB1,CC1,DD1延长后没有交于同一点,故④不正确.
答案:①题型一题型二题型三题型四【例3】 已知,在正三棱锥V-ABC中,底面边长为8,侧棱长为2 ,计算它的高和斜高.
分析本题主要考查正三棱锥中基本量的计算,关键是把已知量与未知量放到直角三角形中求解.题型一题型二题型三题型四解如图所示,设O是底面中心,连接AO并延长,交BC于点D,则D为BC的中点,∴△VAO和△VCD都是直角三角形.题型一题型二题型三题型四反思正棱锥中基本量的计算要借助构造的直角三角形.一般包括高、斜高和底面内切圆半径组成的直角三角形;高、侧棱和底面外接圆半径组成的直角三角形;斜高、侧棱和底面边长的一半组成的直角三角形.
类似地,在正棱台中,有三个重要的直角梯形:两底面中心连线、相应的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和相应两底面正多边形的顶点与中心连线组成一个直角梯形;斜高、侧棱和上、下两底面边长的一半组成一个直角梯形.正棱台的计算问题,实际上就是这几个直角梯形的计算问题.题型一题型二题型三题型四【变式训练3】 一个正四棱台的高是17 cm,上、下底面边长分别为4 cm和16 cm.求这个棱台的侧棱长和斜高.
解:如图所示,取上、下底面的中心O1,O,B1C1和BC的中点E1,E.
连接O1O,OE,EE1,O1E1,OB,O1B1.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,题型一题型二题型三题型四易错点:对概念理解不清而致误
【例4】 下列关于棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
②若过相对棱的两个截面都垂直于底面,则该四棱柱为直四棱柱;
③若侧面两两全等,则该四棱柱为直四棱柱;
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.
其中,真命题的序号是 .?
错解:①②④
错因分析:①中必须是两个相邻的侧面,对概念理解不透彻而误认为①也是正确的.题型一题型二题型三题型四正解:①错,必须是两个相邻的侧面;②正确;③错误,反例:斜四棱柱;④正确,对角线两两相等,则此对角线组成的平行四边形为矩形,故填②④.
答案:②④题型一题型二题型三题型四【变式训练4】 下列命题中:
①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;
②有一个面是多边形,其余各面都是三角形所围成的几何体是棱锥;
③用一个平行于棱锥底面的平面截棱锥,得到的几何体是棱台.
真命题的个数是( )
A.0 B.1 C.2 D.3
解析:命题①②不符合棱柱及棱锥的定义,命题③,用一个平行于棱锥底面的平面去截棱锥,得到的几何体一个是棱台,另一个是棱锥,故③错误.
答案:A1 2 3 4 51.正五棱柱中,若不同在任一侧面且不同在任一底面的两顶点的连线称为它的对角线,则一个正五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
解析:方法一:在上底面选一个点,同时在下底面选一个点,且这两个点不在同一侧面上,这样上底面每个点对应2条对角线,所以共有10条.方法二:过正五棱柱任意不相邻的两条侧棱可得一个截面,每个截面可得到正五棱柱的两条对角线,5个截面共可得到10条对角线.
答案:D1 2 3 4 52.下列说法错误的是( )
A.多面体至少有四个面
B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
解析:多面体中面数最少的是三棱锥,有四个面,故A正确.根据棱柱的结构特征知B正确.长方体、正方体符合棱柱的结构特征,C正确.D中三棱柱的侧面为平行四边形,D错误.
答案:D1 2 3 4 53.如图所示,下列几何体中, 是棱柱, 是棱锥, 是棱台.?
解析:由棱柱、棱锥、棱台的定义知,①②③④符合棱柱的定义;⑥符合棱锥的定义;⑤符合棱台的定义.
答案:①②③④ ⑥ ⑤1 2 3 4 54.说出四棱台有多少个顶点?多少条棱?多少个面?四棱锥呢?
解:作四棱锥P-ABCD,用平行于底面ABCD的平面A1B1C1D1截该棱锥得四棱台ABCD-A1B1C1D1,如图所示,由图得四棱台有8个顶点,12条棱,6个面;四棱锥有5个顶点,8条棱,5个面.1 2 3 4 55.
如图所示,已知该几何体所有的棱长都相等,试分析此几何体的面数、顶点数和棱数,并判断该几何体是不是棱柱、棱锥、棱台的一种.
解:该几何体有8个面,6个顶点,12条棱,它不满足棱柱、棱锥、棱台的定义,故不是棱柱,也不是棱锥,也不是棱台,但它是一个多面体.
