高中数学北师大版必修2第一章立体几何初步1.5.1.1直线与平面平行的判定:26张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.5.1.1直线与平面平行的判定:26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 680.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 21:57:39 | ||
图片预览






文档简介
课件26张PPT。§5 平行关系5.1 平行关系的判定第1课时 直线与平面平行的判定1.掌握线面平行的判定定理.
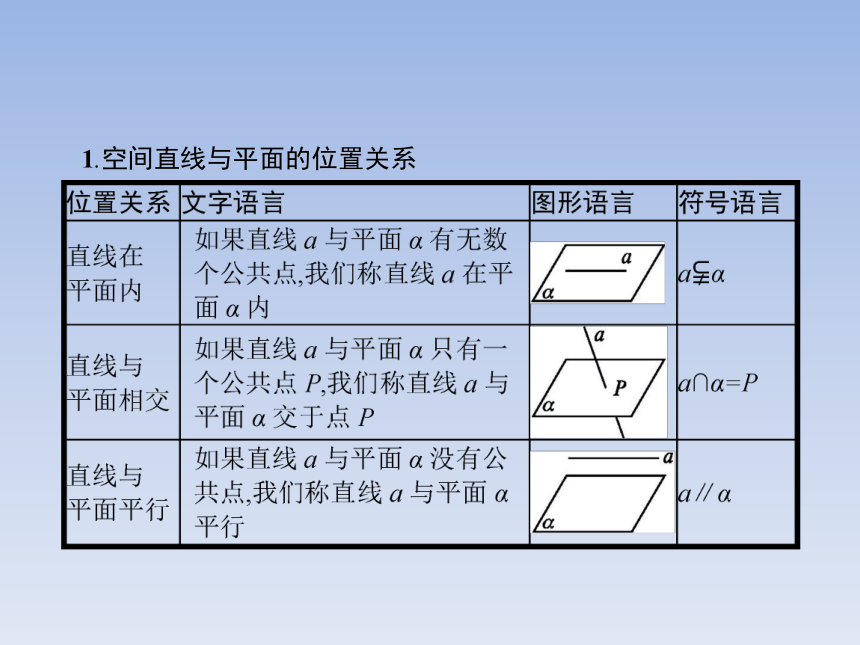
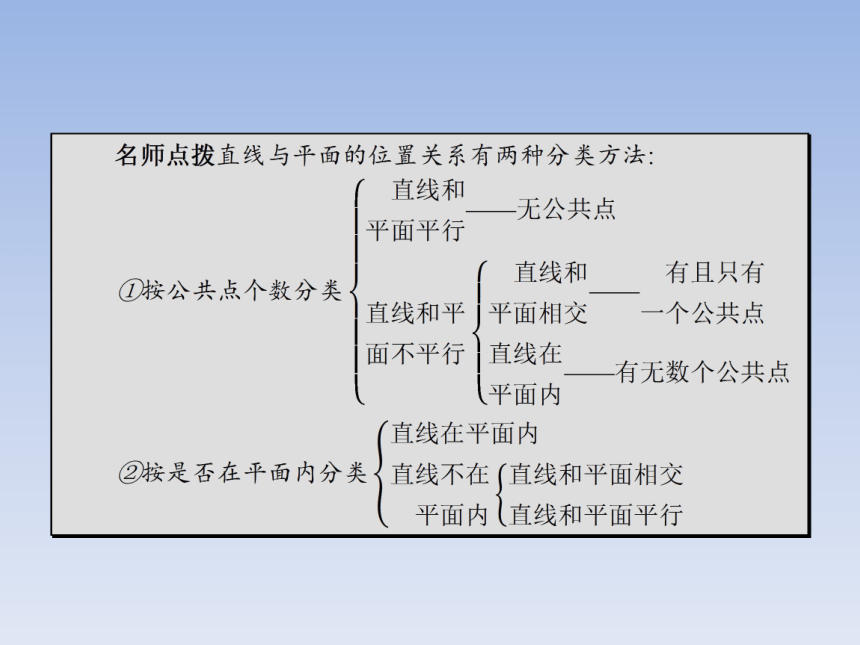
2.会利用线面平行的判定定理证明线面的平行关系.1.空间直线与平面的位置关系 【做一做1】 若直线l在平面α外且直线l上所有的点到平面α的距离都相等,则直线l与平面α的位置关系是 .?
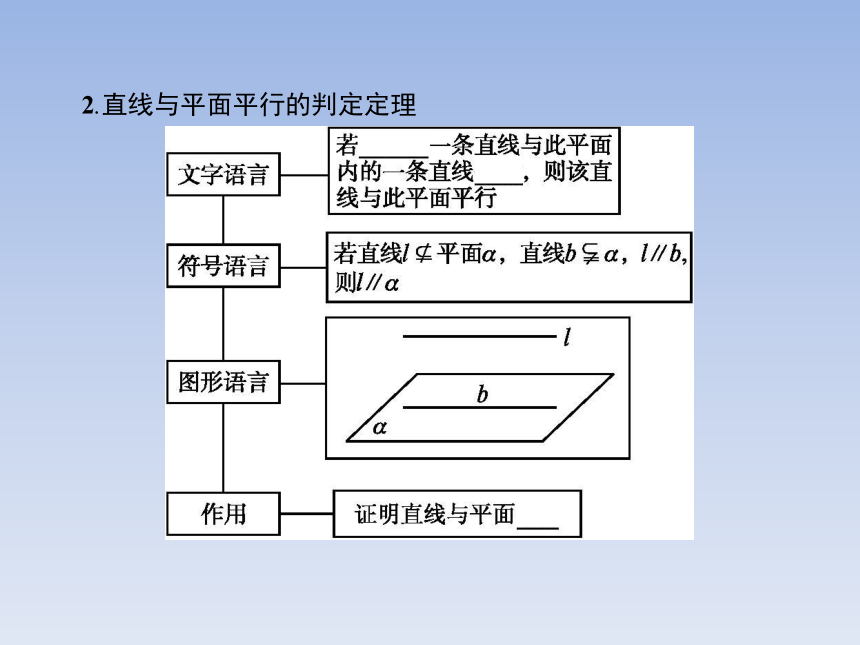
答案:l∥α2.直线与平面平行的判定定理 直线与平面平行的判定定理告诉我们,可以通过直线间的平行来证明直线与平面平行.通常我们将其记为“若线线平行,则线面平行”.因此,对于线面平行的问题通常转化为线线平行的问题来解决.也就是说,证明一条直线和一个平面平行,只要在这个平面内找到一条直线和已知直线平行即可.【做一做2】 在正方体ABCD-A1B1C1D1中,E为DD1的中点.判断体对角线BD1与过点A,C,E的平面的位置关系.
解:如图所示,连接AC,BD.
设AC∩BD=O,易知O为AC,BD的中点.
连接OE,又E为DD1的中点,则OE∥BD1,
连接AE,CE.
∵OE?平面ACE,BD1?平面ACE,
∴BD1∥平面ACE,
即BD1与过点A,C,E的平面是平行关系.题型一题型二题型三【例1】 对于不重合的两条直线m,n和平面α,下列说法正确的是( )
A.如果m?α,n?α,m,n是异面直线,那么n∥α
B.如果m?α,n?α,n∥m,那么n∥α
C.如果m?α,n?α,m,n是异面直线,那么n与α相交
D.如果m∥α,n∥α,m,n共面,那么m∥n题型一题型二题型三解析:如图所示,在长方体ABCD-A1B1C1D1中,直线AB?平面ABCD,CC1?平面ABCD,直线AB和直线CC1是异面直线,但是直线CC1∩平面ABCD=C,排除选项A;直线AB?平面ABCD,直线B1C1?平面ABCD,直线AB和直线B1C1是异面直线,但是直线B1C1∥平面ABCD,排除选项C;直线A1B1∥平面ABCD,直线B1C1∥平面ABCD,直线A1B1和直线B1C1共面,但是A1B1∩B1C1=B1,排除选项D.
答案:B
反思此类题目属于位置关系判定题,并且是用符号语言表示的,是高考考查立体几何知识的主要形式.其解题策略是借助长方体等几何体模型,将符号语言转化为图形语言,利用排除法求解.题型一题型二题型三【变式训练1】 能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A,B∈a,C,D∈b,且AC=BD
D.a?α,b?α,a∥b
解析:A错误,若b?α,a∥b,则a∥α或a?α;
B错误,若b?α,c∥α,a∥b,a∥c,则a∥α或a?α;
C错误,若满足此条件,则a∥α或a?α或a与α相交;
D正确,它们恰好是判定定理所具备的不可缺少的三个条件.
答案:D题型一题型二题型三【例2】 如图所示,在四棱锥S-ABCD中,底面ABCD为正方形,E,F分别为AB,SC的中点.求证:EF∥平面SAD.
分析:要证EF∥平面SAD,只需在平面SAD内找到一条平行于EF的直线即可,又E,F分别为AB,SC的中点,故可以考虑作辅助线,构造平行四边形,从而找到平行于EF并且在平面SAD内的直线.题型一题型二题型三题型一题型二题型三反思用线面平行的判定定理证明线面平行的基本步骤: 题型一题型二题型三【变式训练2】 已知四边形ABCD,ABEF都是正方形,M∈AC,N∈BF,且AM=FN.求证:MN∥平面BCE.题型一题型二题型三易错点:判断平行关系时思维受阻而致误
【例3】
如图所示,在四面体ABCD中,P,Q,M,N分别为AB,BC,DC,DA的中点,截面PQMN是正方形,有下列说法,①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线MN与BD所成的角为45°;⑤QM∥平面ABD.则其中正确的说法是 .(填序号即可)?
错解:①③⑤
错因分析:图中平行关系较多,忽略PQ是△ABC的中位线而得不到PQ∥AC,从而漏选②.题型一题型二题型三正解:对于①,因为截面PQMN是正方形,所以PQ⊥QM,由三角形的中位线性质可得PQ∥AC,QM∥BD.所以由PQ⊥QM,可得AC⊥BD,故①正确;对于②,在△ABC中,P,Q是中点,所以PQ∥AC,可得AC∥截面PQMN,故②正确;对于③,因为截面PQMN为正方形,所以QM=MN,因为P,Q,M,N为中点,所以QM
所以AC=BD,故③正确;对于④,异面直线MN与BD所成的角等于MN与PN所成的角,为90°,故④不正确;对于⑤,QM∥PN,PN?平面ABD,QM?平面ABD,故QM∥平面ABD,故⑤正确.
答案:①②③⑤题型一题型二题型三【变式训练3】 如图所示,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为 .?
解析:因为N,P分别为线段BC,CD的中点,所以NP∥BD,又BD?平面MNP,NP?平面MNP,所以BD∥平面MNP.
答案:平行1 2 3 4 51.过平面外一点,作平面的平行线可以作( )
A.一条
B.两条
C.无数条
D.以上都不对
解析:过平面外一点可作无数条直线与平面内的相应直线平行,故选C.
答案:C1 2 3 4 52有下列命题:
①若直线l平行于平面α内的无数条直线,则l∥α;
②若直线a∥b,b?α,则直线a就平行于平面α内的无数条直线;
③若直线a∥b,b?α,则a∥α;
④若直线a在平面α外,则a∥α.
其中真命题的个数为( )
A.1 B.2 C.3 D.4
解析:①直线l还可能在平面α内.②正确.③直线a还有可能在平面α内.④直线a与平面α相交也满足.
答案:A1 2 3 4 53.若两条直线a∥b,且a∥平面α,则b与α的位置关系是 .?
答案:b∥α或b?α1 2 3 4 54.设m,n是平面α外的两条直线,给出以下三个论断:①m∥n;②m∥α;③n∥α.以其中的两个为条件,余下的一个为结论,构成三个命题,写出你认为正确的一个命题是 .?
解析:由m∥α知,α内必有直线l∥m,
又m∥n,∴n∥l,而n?α,∴n∥α.
因此,由①②?③,同理由①③?②.
答案:①②?③(或①③?②)1 2 3 4 55.如图所示,在长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点,分别连接A1P,AN,PN及C1M.求证:C1M∥平面ANPA1.1 2 3 4 5证明:如图所示,连接AP,因为四边形CC1D1D是矩形,
所以C1D1∥CD,C1D1=CD.
因为N,P分别为线段CD,C1D1的中点,
所以C1P∥CN,C1P=CN.
因为四边形ABCD是矩形,所以AB∥CD,AB=CD.
因为M为线段AB的中点,
所以CN∥AM,CN=AM,
所以C1P∥AM,C1P=AM,
所以四边形AMC1P是平行四边形,所以C1M∥AP.
又C1M?平面ANPA1,AP?平面ANPA1,
所以C1M∥平面ANPA1.
2.会利用线面平行的判定定理证明线面的平行关系.1.空间直线与平面的位置关系 【做一做1】 若直线l在平面α外且直线l上所有的点到平面α的距离都相等,则直线l与平面α的位置关系是 .?
答案:l∥α2.直线与平面平行的判定定理 直线与平面平行的判定定理告诉我们,可以通过直线间的平行来证明直线与平面平行.通常我们将其记为“若线线平行,则线面平行”.因此,对于线面平行的问题通常转化为线线平行的问题来解决.也就是说,证明一条直线和一个平面平行,只要在这个平面内找到一条直线和已知直线平行即可.【做一做2】 在正方体ABCD-A1B1C1D1中,E为DD1的中点.判断体对角线BD1与过点A,C,E的平面的位置关系.
解:如图所示,连接AC,BD.
设AC∩BD=O,易知O为AC,BD的中点.
连接OE,又E为DD1的中点,则OE∥BD1,
连接AE,CE.
∵OE?平面ACE,BD1?平面ACE,
∴BD1∥平面ACE,
即BD1与过点A,C,E的平面是平行关系.题型一题型二题型三【例1】 对于不重合的两条直线m,n和平面α,下列说法正确的是( )
A.如果m?α,n?α,m,n是异面直线,那么n∥α
B.如果m?α,n?α,n∥m,那么n∥α
C.如果m?α,n?α,m,n是异面直线,那么n与α相交
D.如果m∥α,n∥α,m,n共面,那么m∥n题型一题型二题型三解析:如图所示,在长方体ABCD-A1B1C1D1中,直线AB?平面ABCD,CC1?平面ABCD,直线AB和直线CC1是异面直线,但是直线CC1∩平面ABCD=C,排除选项A;直线AB?平面ABCD,直线B1C1?平面ABCD,直线AB和直线B1C1是异面直线,但是直线B1C1∥平面ABCD,排除选项C;直线A1B1∥平面ABCD,直线B1C1∥平面ABCD,直线A1B1和直线B1C1共面,但是A1B1∩B1C1=B1,排除选项D.
答案:B
反思此类题目属于位置关系判定题,并且是用符号语言表示的,是高考考查立体几何知识的主要形式.其解题策略是借助长方体等几何体模型,将符号语言转化为图形语言,利用排除法求解.题型一题型二题型三【变式训练1】 能保证直线a与平面α平行的条件是( )
A.b?α,a∥b
B.b?α,c∥α,a∥b,a∥c
C.b?α,A,B∈a,C,D∈b,且AC=BD
D.a?α,b?α,a∥b
解析:A错误,若b?α,a∥b,则a∥α或a?α;
B错误,若b?α,c∥α,a∥b,a∥c,则a∥α或a?α;
C错误,若满足此条件,则a∥α或a?α或a与α相交;
D正确,它们恰好是判定定理所具备的不可缺少的三个条件.
答案:D题型一题型二题型三【例2】 如图所示,在四棱锥S-ABCD中,底面ABCD为正方形,E,F分别为AB,SC的中点.求证:EF∥平面SAD.
分析:要证EF∥平面SAD,只需在平面SAD内找到一条平行于EF的直线即可,又E,F分别为AB,SC的中点,故可以考虑作辅助线,构造平行四边形,从而找到平行于EF并且在平面SAD内的直线.题型一题型二题型三题型一题型二题型三反思用线面平行的判定定理证明线面平行的基本步骤: 题型一题型二题型三【变式训练2】 已知四边形ABCD,ABEF都是正方形,M∈AC,N∈BF,且AM=FN.求证:MN∥平面BCE.题型一题型二题型三易错点:判断平行关系时思维受阻而致误
【例3】
如图所示,在四面体ABCD中,P,Q,M,N分别为AB,BC,DC,DA的中点,截面PQMN是正方形,有下列说法,①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线MN与BD所成的角为45°;⑤QM∥平面ABD.则其中正确的说法是 .(填序号即可)?
错解:①③⑤
错因分析:图中平行关系较多,忽略PQ是△ABC的中位线而得不到PQ∥AC,从而漏选②.题型一题型二题型三正解:对于①,因为截面PQMN是正方形,所以PQ⊥QM,由三角形的中位线性质可得PQ∥AC,QM∥BD.所以由PQ⊥QM,可得AC⊥BD,故①正确;对于②,在△ABC中,P,Q是中点,所以PQ∥AC,可得AC∥截面PQMN,故②正确;对于③,因为截面PQMN为正方形,所以QM=MN,因为P,Q,M,N为中点,所以QM
所以AC=BD,故③正确;对于④,异面直线MN与BD所成的角等于MN与PN所成的角,为90°,故④不正确;对于⑤,QM∥PN,PN?平面ABD,QM?平面ABD,故QM∥平面ABD,故⑤正确.
答案:①②③⑤题型一题型二题型三【变式训练3】 如图所示,在四面体ABCD中,若M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系为 .?
解析:因为N,P分别为线段BC,CD的中点,所以NP∥BD,又BD?平面MNP,NP?平面MNP,所以BD∥平面MNP.
答案:平行1 2 3 4 51.过平面外一点,作平面的平行线可以作( )
A.一条
B.两条
C.无数条
D.以上都不对
解析:过平面外一点可作无数条直线与平面内的相应直线平行,故选C.
答案:C1 2 3 4 52有下列命题:
①若直线l平行于平面α内的无数条直线,则l∥α;
②若直线a∥b,b?α,则直线a就平行于平面α内的无数条直线;
③若直线a∥b,b?α,则a∥α;
④若直线a在平面α外,则a∥α.
其中真命题的个数为( )
A.1 B.2 C.3 D.4
解析:①直线l还可能在平面α内.②正确.③直线a还有可能在平面α内.④直线a与平面α相交也满足.
答案:A1 2 3 4 53.若两条直线a∥b,且a∥平面α,则b与α的位置关系是 .?
答案:b∥α或b?α1 2 3 4 54.设m,n是平面α外的两条直线,给出以下三个论断:①m∥n;②m∥α;③n∥α.以其中的两个为条件,余下的一个为结论,构成三个命题,写出你认为正确的一个命题是 .?
解析:由m∥α知,α内必有直线l∥m,
又m∥n,∴n∥l,而n?α,∴n∥α.
因此,由①②?③,同理由①③?②.
答案:①②?③(或①③?②)1 2 3 4 55.如图所示,在长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点,分别连接A1P,AN,PN及C1M.求证:C1M∥平面ANPA1.1 2 3 4 5证明:如图所示,连接AP,因为四边形CC1D1D是矩形,
所以C1D1∥CD,C1D1=CD.
因为N,P分别为线段CD,C1D1的中点,
所以C1P∥CN,C1P=CN.
因为四边形ABCD是矩形,所以AB∥CD,AB=CD.
因为M为线段AB的中点,
所以CN∥AM,CN=AM,
所以C1P∥AM,C1P=AM,
所以四边形AMC1P是平行四边形,所以C1M∥AP.
又C1M?平面ANPA1,AP?平面ANPA1,
所以C1M∥平面ANPA1.
