高中数学北师大版必修2第一章立体几何初步1.5.1.2平面与平面平行的判定:23张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.5.1.2平面与平面平行的判定:23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 623.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览








文档简介
课件23张PPT。第2课时 平面与平面平行的判定1.掌握面面平行的判定定理.
2.能利用面面平行的判定定理证明面面的平行关系.平面与平面平行的判定定理
平面与平面平行的判定定理告诉我们,可以通过直线与平面平行来证明平面与平面平行.通常我们将其记为“若线面平行,则面面平行”.名师点拨对两个平面平行的判定定理的三点说明:
(1)两个平面平行是指两个不重合的平面无公共点.
(2)判断平面与平面平行问题可以转化为判断直线与平面平行问题,即要证明两平面平行,只要在其中一个平面内找到两条相交直线都与另一个平面平行,就可断定已知的两个平面平行.
(3)利用判定定理证明两个平面平行时必须具备的两个条件:①有两条直线平行于另一个平面;②这两条直线必须为相交直线.【做一做1】 已知直线l,m,平面α,β,且l?α,m?α,l∥β,m∥β,则α与β的位置关系是( )
A.平行 B.相交
C.平行或相交 D.重合
答案:C
【做一做2】 在正方体ABCD-A'B'C'D'中,与平面ABCD平行的平面是( )
A.平面A'B'C'D' B.平面AA'D'D
C.平面ABB'A' D.平面BCC'B'
答案:A题型一题型二题型三【例1】 判断下列给出的各种说法是否正确?
(1)如果直线a和平面α不相交,那么a∥α;
(2)如果直线a∥平面α,直线b∥a,那么b∥α;
(3)如果直线a∥平面α,那么经过直线a的平面β∥α;
(4)如果平面α内的两条相交直线a和b与平面β内的两条相交直线a'和b'分别平行,那么α∥β.
分析:按照线面平行、面面平行的定义及判定定理对每个命题进行分析判断即可.题型一题型二题型三解:(1)不正确.当直线a和平面α不相交时,可能有a?α,a∥α两种情况,当a?α时,a与α不平行;
(2)不正确.当直线b∥a时,如果b?α,则有b∥α,如果b?α,则没有b∥α;
(3)不正确.当a∥α时,经过直线a的平面β可能与α平行,也可能与α相交;
(4)正确.由线面平行的判定定理,知a∥β,b∥β,且a,b?α,a与b相交,所以必有α∥β.
反思1.运用线面平行、面面平行的判定定理判定结论是否正确时,一定要紧扣两个定理的条件,忽视条件,很容易导致判断错误.
2.在判断一些命题的真假时,一方面要善于列举反例来否定一个命题,另一方面要充分考虑线线关系、线面关系、面面关系中的各种情形,以对一个命题的真假作出合理的判断.题型一题型二题型三 【变式训练1】 设α,β为两个不重合平面,在下列条件中,可判断平面α与β平行的是 .?
①α,β都平行于γ.
②α内存在不共线的三点到β的距离相等.
③l,m是α内的两条直线,且l∥β,m∥β.
④l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β.
解析:①正确.②中如果平面α内三个点在平面β的两侧,满足不共线的三点到平面β的距离相等,此时这两个平面相交,故②错误.③中若l与m平行,则α与β可能相交,故③错误.④正确.
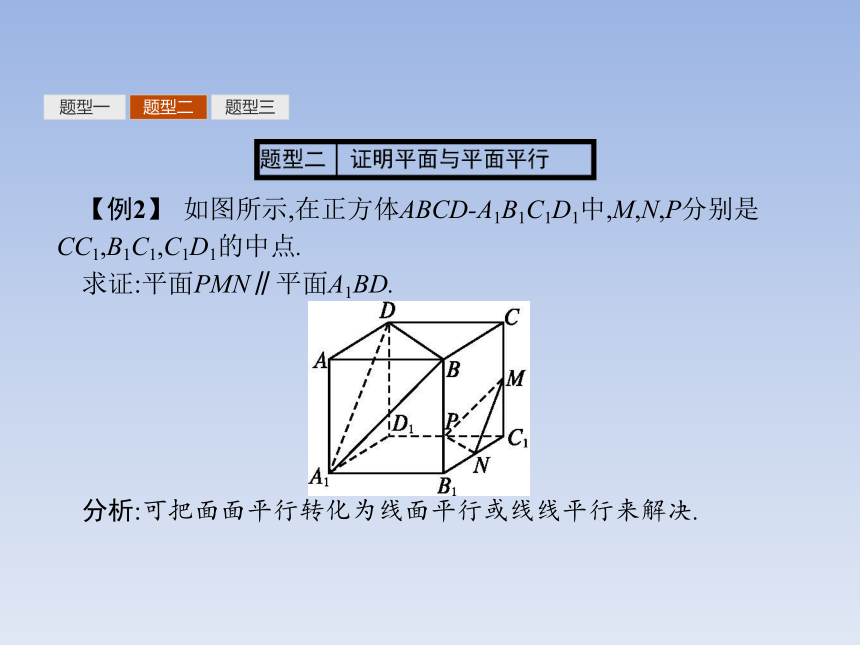
答案:①④题型一题型二题型三【例2】 如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是CC1,B1C1,C1D1的中点.
求证:平面PMN∥平面A1BD.
分析:可把面面平行转化为线面平行或线线平行来解决.题型一题型二题型三证明:如图所示,连接B1D1,B1C.
∵P,N分别是D1C1,B1C1的中点,
∴PN∥B1D1.
又B1D1∥BD,∴PN∥BD.
又PN?平面A1BD,BD?平面A1BD,
∴PN∥平面A1BD.
同理可得MN∥平面A1BD.
又MN∩PN=N,
∴平面PMN∥平面A1BD.
反思证明平面与平面平行的方法:
(1)利用定义,证明面面无公共点.
(2)利用面面平行的判定定理转化为证明线面平行,即证明一个平面内的两条相交直线都平行于另一个平面.题型一题型二题型三【变式训练2】 如图所示,若本例中去掉侧棱上的三个中点,如何证明平面AB1D1∥平面C1BD?
∴四边形BDD1B1为平行四边形,
∴BD∥B1D1.
又B1D1?平面C1BD,BD?平面C1BD,
∴B1D1∥平面C1BD.
同理可得AD1∥平面C1BD.
又B1D1∩AD1=D1,
∴平面AB1D1∥平面C1BD.题型一题型二题型三【例3】 如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,试说明当点Q在什么位置时,平面D1BQ∥平面PAO.
分析:由P是DD1的中点,猜想Q应是CC1的中点.题型一题型二题型三解:当Q为CC1的中点时,平面D1BQ∥平面PAO.
证明如下:
设Q为CC1的中点,
可知四边形ABQP是平行四边形,
∴AP∥BQ.
∵AP?平面D1BQ,BQ?平面D1BQ,
∴AP∥平面D1BQ.
∵O,P分别为BD,DD1的中点,∴OP∥BD1.
又OP?平面D1BQ,BD1?平面D1BQ,
∴OP∥平面D1BQ.
又AP∩PO=P,∴平面D1BQ∥平面PAO,
∴当Q为CC1的中点时,平面D1BQ∥平面PAO.题型一题型二题型三反思对于条件缺失的探索性问题,解答过程中要明确目的,结合题目本身的特点与相应的定理大胆地猜想,然后加以证明.特别要注意中点、顶点等特殊点.题型一题型二题型三【变式训练3】
如图所示,在四棱锥P-ABCD中,AB∥CD,且AB=2CD,E为PB的中点.
(1)求证:CE∥平面PAD.
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论;若不存在,说明理由.题型一题型二题型三图① 题型一题型二题型三1 2 3 41.若直线l∥平面α,直线m∥平面α,直线l与m相交于点P,且l与m确定的平面为β,则α与β的位置关系是( )
A.相交 B.平行
C.重合 D.平行或相交
答案:B1 2 3 42.下列命题中正确的是( )
①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;
③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线都平行于另一个平面,则这两个平面平行.
A.①③ B.②④ C.②③④ D.③④1 2 3 4解析:如图所示,在长方体ABCD-A1B1C1D1中,在平面ABCD内,在AB上任取一点E,过点E作EF∥AD交CD于F,则由线面平行的判定定理知,EF,BC都平行于平面ADD1A1.
用同样的方法可以在平面ABCD内作出无数
条直线都与平面ADD1A1平行,但是平面ABCD
与平面ADD1A1不平行.
因此,命题①②都不正确.
命题③正确,事实上,因为一个平面内任意一条直线都平行于另一个平面,所以这两个平面必无公共点(要注意“任意一条直线”与“无数条直线”的区别).
命题④是平面与平面平行的判定定理,故正确.
答案:D1 2 3 43.已知直线a,b,c为三条不重合的直线,平面α,β,γ为三个不重合平面,则以下三个命题:
①a∥c,b∥c?a∥b;②γ∥α,β∥α?γ∥β;③a∥γ,α∥γ?a∥α.
其中正确命题的序号是 .?
解析:由平行公理,知①正确;由平面平行的传递性知②正确;③不正确,因为a可能在α内.
答案:①②1 2 3 44.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点.求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.1 2 3 4证明:(1)如图所示,连接SB.
∵E,G分别是BC,SC的中点,∴EG∥SB.
又SB?平面BDD1B1,EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.
(2)如图所示,连接SD.
∵F,G分别是DC,SC的中点,∴FG∥SD.
又SD?平面BDD1B1,FG?平面BDD1B1,
∴直线FG∥平面BDD1B1.
又EG∥平面BDD1B1,且直线EG?平面EFG,直线FG?平面EFG,直线EG∩直线FG=G,
∴平面EFG∥平面BDD1B1.
2.能利用面面平行的判定定理证明面面的平行关系.平面与平面平行的判定定理
平面与平面平行的判定定理告诉我们,可以通过直线与平面平行来证明平面与平面平行.通常我们将其记为“若线面平行,则面面平行”.名师点拨对两个平面平行的判定定理的三点说明:
(1)两个平面平行是指两个不重合的平面无公共点.
(2)判断平面与平面平行问题可以转化为判断直线与平面平行问题,即要证明两平面平行,只要在其中一个平面内找到两条相交直线都与另一个平面平行,就可断定已知的两个平面平行.
(3)利用判定定理证明两个平面平行时必须具备的两个条件:①有两条直线平行于另一个平面;②这两条直线必须为相交直线.【做一做1】 已知直线l,m,平面α,β,且l?α,m?α,l∥β,m∥β,则α与β的位置关系是( )
A.平行 B.相交
C.平行或相交 D.重合
答案:C
【做一做2】 在正方体ABCD-A'B'C'D'中,与平面ABCD平行的平面是( )
A.平面A'B'C'D' B.平面AA'D'D
C.平面ABB'A' D.平面BCC'B'
答案:A题型一题型二题型三【例1】 判断下列给出的各种说法是否正确?
(1)如果直线a和平面α不相交,那么a∥α;
(2)如果直线a∥平面α,直线b∥a,那么b∥α;
(3)如果直线a∥平面α,那么经过直线a的平面β∥α;
(4)如果平面α内的两条相交直线a和b与平面β内的两条相交直线a'和b'分别平行,那么α∥β.
分析:按照线面平行、面面平行的定义及判定定理对每个命题进行分析判断即可.题型一题型二题型三解:(1)不正确.当直线a和平面α不相交时,可能有a?α,a∥α两种情况,当a?α时,a与α不平行;
(2)不正确.当直线b∥a时,如果b?α,则有b∥α,如果b?α,则没有b∥α;
(3)不正确.当a∥α时,经过直线a的平面β可能与α平行,也可能与α相交;
(4)正确.由线面平行的判定定理,知a∥β,b∥β,且a,b?α,a与b相交,所以必有α∥β.
反思1.运用线面平行、面面平行的判定定理判定结论是否正确时,一定要紧扣两个定理的条件,忽视条件,很容易导致判断错误.
2.在判断一些命题的真假时,一方面要善于列举反例来否定一个命题,另一方面要充分考虑线线关系、线面关系、面面关系中的各种情形,以对一个命题的真假作出合理的判断.题型一题型二题型三 【变式训练1】 设α,β为两个不重合平面,在下列条件中,可判断平面α与β平行的是 .?
①α,β都平行于γ.
②α内存在不共线的三点到β的距离相等.
③l,m是α内的两条直线,且l∥β,m∥β.
④l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β.
解析:①正确.②中如果平面α内三个点在平面β的两侧,满足不共线的三点到平面β的距离相等,此时这两个平面相交,故②错误.③中若l与m平行,则α与β可能相交,故③错误.④正确.
答案:①④题型一题型二题型三【例2】 如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是CC1,B1C1,C1D1的中点.
求证:平面PMN∥平面A1BD.
分析:可把面面平行转化为线面平行或线线平行来解决.题型一题型二题型三证明:如图所示,连接B1D1,B1C.
∵P,N分别是D1C1,B1C1的中点,
∴PN∥B1D1.
又B1D1∥BD,∴PN∥BD.
又PN?平面A1BD,BD?平面A1BD,
∴PN∥平面A1BD.
同理可得MN∥平面A1BD.
又MN∩PN=N,
∴平面PMN∥平面A1BD.
反思证明平面与平面平行的方法:
(1)利用定义,证明面面无公共点.
(2)利用面面平行的判定定理转化为证明线面平行,即证明一个平面内的两条相交直线都平行于另一个平面.题型一题型二题型三【变式训练2】 如图所示,若本例中去掉侧棱上的三个中点,如何证明平面AB1D1∥平面C1BD?
∴四边形BDD1B1为平行四边形,
∴BD∥B1D1.
又B1D1?平面C1BD,BD?平面C1BD,
∴B1D1∥平面C1BD.
同理可得AD1∥平面C1BD.
又B1D1∩AD1=D1,
∴平面AB1D1∥平面C1BD.题型一题型二题型三【例3】 如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,试说明当点Q在什么位置时,平面D1BQ∥平面PAO.
分析:由P是DD1的中点,猜想Q应是CC1的中点.题型一题型二题型三解:当Q为CC1的中点时,平面D1BQ∥平面PAO.
证明如下:
设Q为CC1的中点,
可知四边形ABQP是平行四边形,
∴AP∥BQ.
∵AP?平面D1BQ,BQ?平面D1BQ,
∴AP∥平面D1BQ.
∵O,P分别为BD,DD1的中点,∴OP∥BD1.
又OP?平面D1BQ,BD1?平面D1BQ,
∴OP∥平面D1BQ.
又AP∩PO=P,∴平面D1BQ∥平面PAO,
∴当Q为CC1的中点时,平面D1BQ∥平面PAO.题型一题型二题型三反思对于条件缺失的探索性问题,解答过程中要明确目的,结合题目本身的特点与相应的定理大胆地猜想,然后加以证明.特别要注意中点、顶点等特殊点.题型一题型二题型三【变式训练3】
如图所示,在四棱锥P-ABCD中,AB∥CD,且AB=2CD,E为PB的中点.
(1)求证:CE∥平面PAD.
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论;若不存在,说明理由.题型一题型二题型三图① 题型一题型二题型三1 2 3 41.若直线l∥平面α,直线m∥平面α,直线l与m相交于点P,且l与m确定的平面为β,则α与β的位置关系是( )
A.相交 B.平行
C.重合 D.平行或相交
答案:B1 2 3 42.下列命题中正确的是( )
①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;
③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线都平行于另一个平面,则这两个平面平行.
A.①③ B.②④ C.②③④ D.③④1 2 3 4解析:如图所示,在长方体ABCD-A1B1C1D1中,在平面ABCD内,在AB上任取一点E,过点E作EF∥AD交CD于F,则由线面平行的判定定理知,EF,BC都平行于平面ADD1A1.
用同样的方法可以在平面ABCD内作出无数
条直线都与平面ADD1A1平行,但是平面ABCD
与平面ADD1A1不平行.
因此,命题①②都不正确.
命题③正确,事实上,因为一个平面内任意一条直线都平行于另一个平面,所以这两个平面必无公共点(要注意“任意一条直线”与“无数条直线”的区别).
命题④是平面与平面平行的判定定理,故正确.
答案:D1 2 3 43.已知直线a,b,c为三条不重合的直线,平面α,β,γ为三个不重合平面,则以下三个命题:
①a∥c,b∥c?a∥b;②γ∥α,β∥α?γ∥β;③a∥γ,α∥γ?a∥α.
其中正确命题的序号是 .?
解析:由平行公理,知①正确;由平面平行的传递性知②正确;③不正确,因为a可能在α内.
答案:①②1 2 3 44.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点.求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.1 2 3 4证明:(1)如图所示,连接SB.
∵E,G分别是BC,SC的中点,∴EG∥SB.
又SB?平面BDD1B1,EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.
(2)如图所示,连接SD.
∵F,G分别是DC,SC的中点,∴FG∥SD.
又SD?平面BDD1B1,FG?平面BDD1B1,
∴直线FG∥平面BDD1B1.
又EG∥平面BDD1B1,且直线EG?平面EFG,直线FG?平面EFG,直线EG∩直线FG=G,
∴平面EFG∥平面BDD1B1.
