高中数学北师大版必修2第一章立体几何初步1.6.1.1直线与平面垂直的判定:26张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.6.1.1直线与平面垂直的判定:26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 676.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览








文档简介
课件26张PPT。§6 垂直关系6.1 垂直关系的判定第1课时 直线与平面垂直的判定1.理解直线与平面垂直的概念.
2.掌握直线与平面垂直的判定定理.
3.能运用直线与平面垂直的判定定理证明线面垂直.直线与平面垂直
(1)定义:如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直.
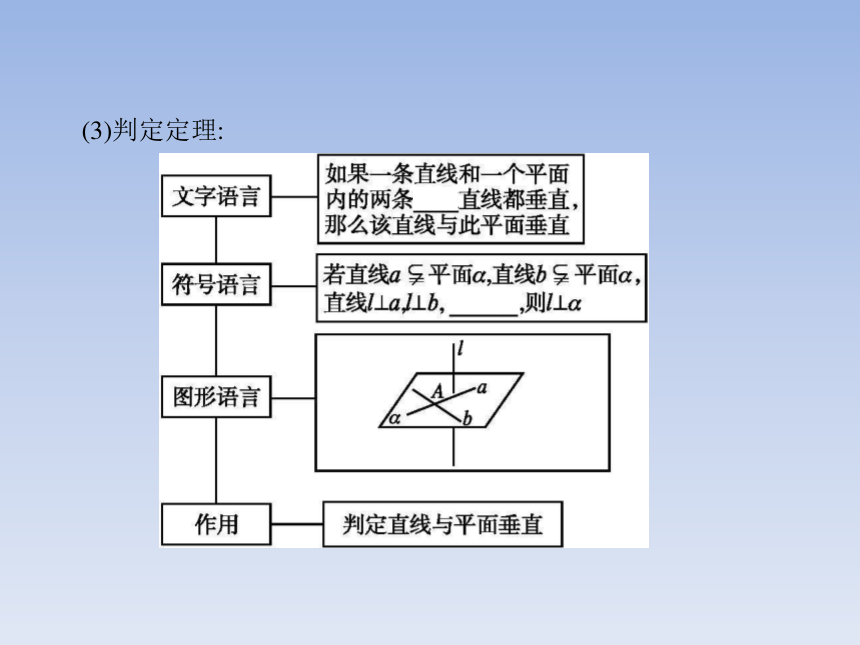
(2)画法:当直线与平面垂直时,通常把表示直线的线段画成和表示平面的平行四边形的横边垂直.如图所示.(3)判定定理: 名师点拨1.直线和平面垂直的定义是描述性定义,“任何一条”与“所有”表达相同的含义.
2.直线与平面垂直是直线与平面相交的特例.
3.由定义可得线面垂直?线线垂直,即若a⊥α,b?α,则a⊥b.
4.直线与平面垂直的判定定理告诉我们要证线面垂直可通过线线垂直来完成.
5.由公理4可知平行具有传递性,因此两条平行直线中的一条垂直于这个平面,则另一条也垂直于这个平面.【做一做1】 直线l垂直于平面α内的无数条直线,则 ( )
A.l⊥α B.l?α
C.l∥α D.以上均有可能
答案:D
【做一做2】 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥BC,PD=1,PC=
求证:PD⊥平面ABCD.
证明:∵PD=DC=1,PC=
∴△PDC是直角三角形.
∴PD⊥CD.
又PD⊥BC,BC∩CD=C,BC?平面ABCD,CD?平面ABCD,
∴PD⊥平面ABCD.题型一题型二题型三【例1】 有下列说法:
①已知三棱锥P-ABC的高为PO,且PA=PB=PC,则点O为△ABC的外心;
②如果直线l与平面α不垂直,那么在α内不存在与l垂直的直线;
③过直线外一点有且只有一个平面与已知直线垂直;
④与一个平面的垂线垂直的直线和这个平面平行;
⑤过平面外一点和这个平面垂直的直线有且只有一条.
其中正确说法的序号是 .?题型一题型二题型三解析: 答案:①③⑤ 题型一题型二题型三反思在平面几何中,我们有结论:经过一点,有且只有一条直线与已知直线垂直.在立体几何中,也有类似的重要结论:
结论1:过一点和已知平面垂直的直线有且只有一条.
结论2:过一点和已知直线垂直的平面有且只有一个.题型一题型二题型三【变式训练1】 下列命题正确的是( )
A.如果一条直线垂直于平面内的一条直线,那么这条直线和这个平面垂直
B.如果一条直线垂直于一个平面内的两条直线,那么这条直线和这个平面垂直
C.如果一条直线垂直于一个平面内的无数条直线,那么这条直线和这个平面垂直
D.如果一条直线垂直于一个平面内的任意一条直线,那么这条直线和这个平面垂直题型一题型二题型三解析:本题主要考查直线和平面垂直的概念,解决本题关键是理解概念的本质.我们以正方体ABCD-A1B1C1D1为例,如图.
直线A1C1⊥BD,且A1C1与平面ABCD内的和BD平行的直线都垂直,而A1C1与平面ABCD平行,故选项A,B,C错,正确答案是D.
答案:D题型一题型二题型三【例2】 在正方体ABCD-A1B1C1D1中,棱长为1,E是BB1的中点,O是底面正方形ABCD的中心.
求证:OE⊥平面ACD1.
分析:只需证OE⊥AC,OE⊥D1O即可.其中OE⊥AC易证,通过计算可得D1E2=D1O2+OE2,从而得到OE⊥OD1.题型一题型二题型三题型一题型二题型三反思要善于利用平面图形的性质构造线线垂直关系,如等腰三角形底边上的中线、菱形的对角线、勾股定理的逆定理等,这是证明空间垂直关系的基础,解题时要善于挖掘题中隐含条件.题型一题型二题型三【变式训练2】 如图,已知PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上不同于A和B的任意一点,过点A作AE⊥PC于点E.
求证:AE⊥平面PBC.
证明:∵PA⊥平面ABC,∴PA⊥BC.
又AB是☉O的直径,∴BC⊥AC.
而PA∩AC=A,∴BC⊥平面PAC.
又AE?平面PAC,∴BC⊥AE.
∵PC⊥AE且PC∩BC=C,∴AE⊥平面PBC.题型一题型二题型三易错点:推理不严密而致误
【例3】 如图所示,已知α∩β=l,PA⊥α于点A,PB⊥β于点B,AQ⊥l于点Q,连接BQ.
求证:l⊥BQ.
错解:∵α∩β=l,l?α,l?β,
又PA⊥α,∴PA⊥l.
∵PB⊥β,∴PB⊥l.
而PA∩PB=P,∴l⊥平面PAQB,∴l⊥BQ.
错因分析:PA∩PB=P,则PA与PB确定一个平面,此时还不能确定点Q是否在平面PAB内,题中不加证明,就认为点Q在平面PAB内.显然是错误的.题设中还有条件AQ⊥l,显然如果没有AQ⊥l,那么BQ就不可能垂直于l.题型一题型二题型三正解:连接AB,∵α∩β=l,PA⊥α,PB⊥β,
∴PA⊥l,PB⊥l.
又PA∩PB=P,∴l⊥平面PAB,∴l⊥AB.
又AQ⊥l,而AQ∩AB=A,
∴l⊥平面ABQ,∴l⊥BQ.题型一题型二题型三【变式训练3】
题型一题型二题型三证明:如图所示,连接PE,EC,在Rt△PAE和Rt△CDE中,PA=AB=CD,AE=DE,
所以PE=CE,即△PEC是等腰三角形.
又F是底边PC的中点,所以EF⊥PC.
F是PC的中点,所以BF⊥PC.
又BF∩EF=F,所以PC⊥平面BEF.1 2 3 41.若一条直线和三角形的两边同时垂直,则这条直线和这个三角形的第三边的位置关系是( )
A.平行 B.垂直
C.相交不垂直 D.不确定
解析:如果一条直线垂直于三角形的两条边,那么必垂直于这个三角形所在平面,因而必与第三边垂直.
答案:B1 2 3 42.在正方体ABCD-A1B1C1D1的六个面中,与AA1垂直的面的个数是( )
A.1 B.2 C.3 D.6
答案:B1 2 3 43.在三棱锥P-ABC中,最多有 个直角三角形.?
解析:如图所示,不妨设PA⊥AB,PA⊥AC,则△APB和△PAC均为直角三角形.
由线面垂直的判定定理知,PA⊥平面ABC,即PA⊥BC,若∠ABC=90°,则BC⊥AB,
∴BC⊥面PBA,即∠PBC=90°.
∴△ABC,△PBC为直角三角形,
故直角三角形最多有4个.
答案:41 2 3 44.如图所示,在正方体A1B1C1D1-ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心.
求证:EF⊥平面BB1O.1 2 3 4证明:如图所示,连接AC,BD,则O为AC和BD的交点,OB与OD在一条直线上.
∵四边形ABCD是正方形,∴AC⊥BO.
又B1B⊥平面ABCD,AC?平面ABCD,
∴BB1⊥AC.
又BO∩BB1=B,∴AC⊥平面BB1O.
又E,F分别是AB,BC的中点,
∴在△ABC中,EF∥AC.
∴EF⊥平面BB1O.
2.掌握直线与平面垂直的判定定理.
3.能运用直线与平面垂直的判定定理证明线面垂直.直线与平面垂直
(1)定义:如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直.
(2)画法:当直线与平面垂直时,通常把表示直线的线段画成和表示平面的平行四边形的横边垂直.如图所示.(3)判定定理: 名师点拨1.直线和平面垂直的定义是描述性定义,“任何一条”与“所有”表达相同的含义.
2.直线与平面垂直是直线与平面相交的特例.
3.由定义可得线面垂直?线线垂直,即若a⊥α,b?α,则a⊥b.
4.直线与平面垂直的判定定理告诉我们要证线面垂直可通过线线垂直来完成.
5.由公理4可知平行具有传递性,因此两条平行直线中的一条垂直于这个平面,则另一条也垂直于这个平面.【做一做1】 直线l垂直于平面α内的无数条直线,则 ( )
A.l⊥α B.l?α
C.l∥α D.以上均有可能
答案:D
【做一做2】 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥BC,PD=1,PC=
求证:PD⊥平面ABCD.
证明:∵PD=DC=1,PC=
∴△PDC是直角三角形.
∴PD⊥CD.
又PD⊥BC,BC∩CD=C,BC?平面ABCD,CD?平面ABCD,
∴PD⊥平面ABCD.题型一题型二题型三【例1】 有下列说法:
①已知三棱锥P-ABC的高为PO,且PA=PB=PC,则点O为△ABC的外心;
②如果直线l与平面α不垂直,那么在α内不存在与l垂直的直线;
③过直线外一点有且只有一个平面与已知直线垂直;
④与一个平面的垂线垂直的直线和这个平面平行;
⑤过平面外一点和这个平面垂直的直线有且只有一条.
其中正确说法的序号是 .?题型一题型二题型三解析: 答案:①③⑤ 题型一题型二题型三反思在平面几何中,我们有结论:经过一点,有且只有一条直线与已知直线垂直.在立体几何中,也有类似的重要结论:
结论1:过一点和已知平面垂直的直线有且只有一条.
结论2:过一点和已知直线垂直的平面有且只有一个.题型一题型二题型三【变式训练1】 下列命题正确的是( )
A.如果一条直线垂直于平面内的一条直线,那么这条直线和这个平面垂直
B.如果一条直线垂直于一个平面内的两条直线,那么这条直线和这个平面垂直
C.如果一条直线垂直于一个平面内的无数条直线,那么这条直线和这个平面垂直
D.如果一条直线垂直于一个平面内的任意一条直线,那么这条直线和这个平面垂直题型一题型二题型三解析:本题主要考查直线和平面垂直的概念,解决本题关键是理解概念的本质.我们以正方体ABCD-A1B1C1D1为例,如图.
直线A1C1⊥BD,且A1C1与平面ABCD内的和BD平行的直线都垂直,而A1C1与平面ABCD平行,故选项A,B,C错,正确答案是D.
答案:D题型一题型二题型三【例2】 在正方体ABCD-A1B1C1D1中,棱长为1,E是BB1的中点,O是底面正方形ABCD的中心.
求证:OE⊥平面ACD1.
分析:只需证OE⊥AC,OE⊥D1O即可.其中OE⊥AC易证,通过计算可得D1E2=D1O2+OE2,从而得到OE⊥OD1.题型一题型二题型三题型一题型二题型三反思要善于利用平面图形的性质构造线线垂直关系,如等腰三角形底边上的中线、菱形的对角线、勾股定理的逆定理等,这是证明空间垂直关系的基础,解题时要善于挖掘题中隐含条件.题型一题型二题型三【变式训练2】 如图,已知PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上不同于A和B的任意一点,过点A作AE⊥PC于点E.
求证:AE⊥平面PBC.
证明:∵PA⊥平面ABC,∴PA⊥BC.
又AB是☉O的直径,∴BC⊥AC.
而PA∩AC=A,∴BC⊥平面PAC.
又AE?平面PAC,∴BC⊥AE.
∵PC⊥AE且PC∩BC=C,∴AE⊥平面PBC.题型一题型二题型三易错点:推理不严密而致误
【例3】 如图所示,已知α∩β=l,PA⊥α于点A,PB⊥β于点B,AQ⊥l于点Q,连接BQ.
求证:l⊥BQ.
错解:∵α∩β=l,l?α,l?β,
又PA⊥α,∴PA⊥l.
∵PB⊥β,∴PB⊥l.
而PA∩PB=P,∴l⊥平面PAQB,∴l⊥BQ.
错因分析:PA∩PB=P,则PA与PB确定一个平面,此时还不能确定点Q是否在平面PAB内,题中不加证明,就认为点Q在平面PAB内.显然是错误的.题设中还有条件AQ⊥l,显然如果没有AQ⊥l,那么BQ就不可能垂直于l.题型一题型二题型三正解:连接AB,∵α∩β=l,PA⊥α,PB⊥β,
∴PA⊥l,PB⊥l.
又PA∩PB=P,∴l⊥平面PAB,∴l⊥AB.
又AQ⊥l,而AQ∩AB=A,
∴l⊥平面ABQ,∴l⊥BQ.题型一题型二题型三【变式训练3】
题型一题型二题型三证明:如图所示,连接PE,EC,在Rt△PAE和Rt△CDE中,PA=AB=CD,AE=DE,
所以PE=CE,即△PEC是等腰三角形.
又F是底边PC的中点,所以EF⊥PC.
F是PC的中点,所以BF⊥PC.
又BF∩EF=F,所以PC⊥平面BEF.1 2 3 41.若一条直线和三角形的两边同时垂直,则这条直线和这个三角形的第三边的位置关系是( )
A.平行 B.垂直
C.相交不垂直 D.不确定
解析:如果一条直线垂直于三角形的两条边,那么必垂直于这个三角形所在平面,因而必与第三边垂直.
答案:B1 2 3 42.在正方体ABCD-A1B1C1D1的六个面中,与AA1垂直的面的个数是( )
A.1 B.2 C.3 D.6
答案:B1 2 3 43.在三棱锥P-ABC中,最多有 个直角三角形.?
解析:如图所示,不妨设PA⊥AB,PA⊥AC,则△APB和△PAC均为直角三角形.
由线面垂直的判定定理知,PA⊥平面ABC,即PA⊥BC,若∠ABC=90°,则BC⊥AB,
∴BC⊥面PBA,即∠PBC=90°.
∴△ABC,△PBC为直角三角形,
故直角三角形最多有4个.
答案:41 2 3 44.如图所示,在正方体A1B1C1D1-ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心.
求证:EF⊥平面BB1O.1 2 3 4证明:如图所示,连接AC,BD,则O为AC和BD的交点,OB与OD在一条直线上.
∵四边形ABCD是正方形,∴AC⊥BO.
又B1B⊥平面ABCD,AC?平面ABCD,
∴BB1⊥AC.
又BO∩BB1=B,∴AC⊥平面BB1O.
又E,F分别是AB,BC的中点,
∴在△ABC中,EF∥AC.
∴EF⊥平面BB1O.
