高中数学北师大版必修2第一章立体几何初步1.6.2垂直关系的性质:30张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.6.2垂直关系的性质:30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 695.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览










文档简介
课件30张PPT。6.2 垂直关系的性质1.理解并掌握直线与平面垂直、平面与平面垂直的性质定理.
2.会用两个性质定理解决相关问题.
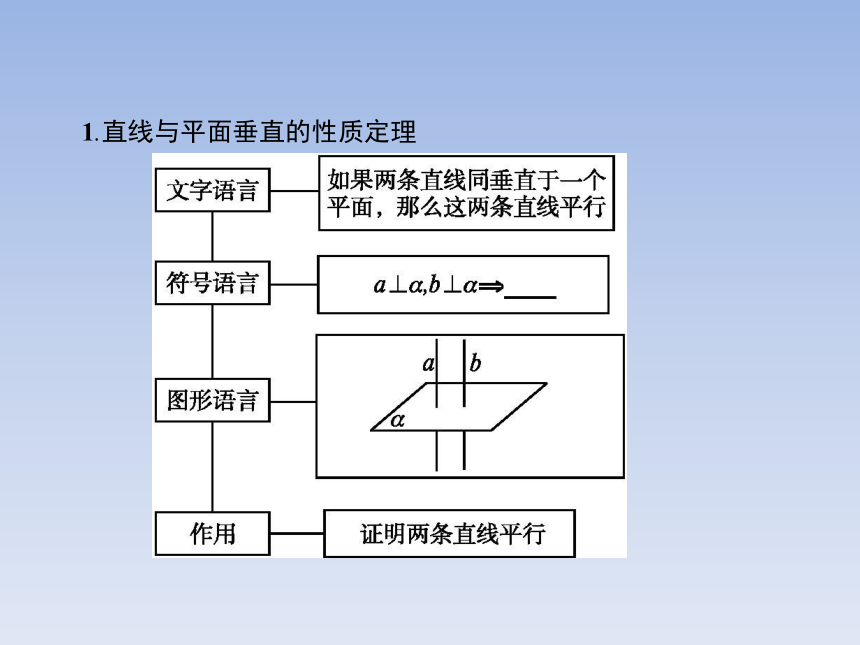
3.理解线线垂直、线面垂直、面面垂直的内在联系.1.直线与平面垂直的性质定理 名师点拨1.利用线面垂直的性质来证明线线平行时,其关键是找出一个平面,使所证直线都与该平面垂直.
2.线面垂直的性质定理、线面平行的性质定理、平行于同一直线的两条直线平行都是证明线线平行的依据.证明线面平行、面面平行,归结到最后还是证明线线平行.
3.垂直于同一直线的两个平面互相平行.2.平面与平面垂直的性质定理 名师点拨1.应用面面垂直的性质定理时必须注意到两个条件:(1)线在平面内;(2)线垂直于两平面的交线,因此找准两平面的交线是关键.
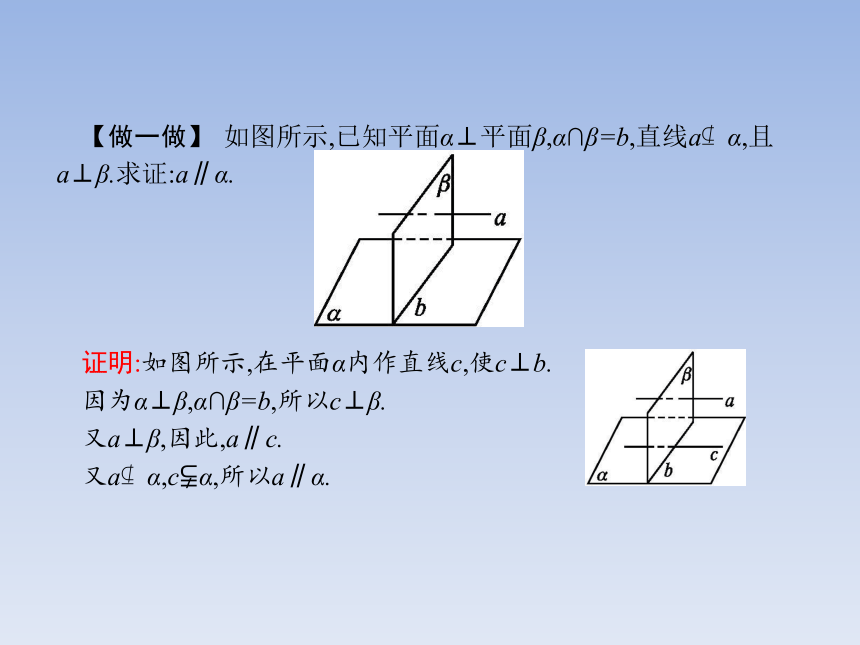
2.已知面面垂直的条件,其性质定理就给出了作辅助线的一种方法,设法找出(作出)一个平面内的一条直线垂直于它们的交线,就可得到线面垂直的结论.【做一做】 如图所示,已知平面α⊥平面β,α∩β=b,直线a?α,且a⊥β.求证:a∥α.
证明:如图所示,在平面α内作直线c,使c⊥b.
因为α⊥β,α∩β=b,所以c⊥β.
又a⊥β,因此,a∥c.
又a?α,c?α,所以a∥α.题型一题型二题型三题型四【例1】 已知直线m,n,平面α,β,下列说法正确的是 ( )
A.m⊥α,n?β,m⊥n,则α⊥β
B.α⊥β,m⊥α,n∥β,则m⊥n
C.α∥β,m⊥α,n∥β,则m⊥n
D.α⊥β,α∩β=m,m⊥n,则n⊥β题型一题型二题型三题型四解析:如图所示,在正方体ABCD- A1B1C1D1中,直线C1C⊥平面ABCD,直线D1C1?平面A1B1C1D1,直线C1C⊥直线D1C1,但是平面ABCD与平面A1B1C1D1平行,排除A选项;平面ABCD⊥平面D1DCC1,直线C1C⊥平面ABCD,B1B∥平面D1DCC1,但是B1B∥C1C,排除B选项;平面ABCD⊥平面A1ABB1,平面ABCD∩平面A1ABB1=AB,AB⊥BC1,但是BC1不垂直于平面A1ABB1,排除D选项.
答案:C
反思本题是符号语言表述的位置关系的判断题,以选择题的形式出现,通常借助几何模型,利用排除法,排除错误的选项.题型一题型二题型三题型四【变式训练1】 已知平面α⊥平面β,m是α内一条直线,n是β内一条直线,且m⊥n,那么:①m⊥β;②n⊥α;③m⊥β或n⊥α;④m⊥β且n⊥α.这四个结论中,不正确的三个是( )
A.①②③ B.①②④
C.①③④ D.②③④
解析:本题主要考查面面垂直的性质和线面垂直的判定,解决问题的关键是正确理解定理的条件及结论.在正方体ABCD-A1B1C1D1中,令平面ABCD和平面CDD1C1分别为α和β,若m为AB,n为CC1,则m⊥n,但m∥β,故①错误;同理②④错误.故选B.
答案:B题型一题型二题型三题型四【例2】 如图所示,在正方体ABCD- A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.
求证:EF∥BD1.
分析:题目条件中给出了线线垂直,通过转化可证得线面垂直,要证EF∥BD1,只需证明EF与BD1同垂直于某一平面即可,由条件可知这里选择平面AB1C.题型一题型二题型三题型四证明:连接AB1,B1C,BD,B1D1,如图所示.
∵DD1⊥平面ABCD,AC?平面ABCD,∴DD1⊥AC.
又AC⊥BD,∴AC⊥平面BDD1B1.
∵BD1?平面BDD1B1,∴AC⊥BD1.
同理BD1⊥B1C,又AC∩B1C=C,
∴BD1⊥平面AB1C.
∵EF⊥A1D,且A1D∥B1C,∴EF⊥B1C.
又EF⊥AC,且AC ∩B1C=C,∴EF⊥平面AB1C.
∴EF∥BD1.
反思当题中垂直条件很多,但又需证明两条直线平行时,就要考虑用直线与平面垂直的性质定理,从而完成由垂直向平行的转化.题型一题型二题型三题型四【变式训练2】 (1)本例中的“正方体ABCD-A1B1C1D1”换为“长方体ABCD-A1B1C1D1”,结论“EF∥BD1”还成立吗?
(2)本例中去掉点E,点F,线段A1D,若AC与BD的交点为O,DD1的中点为G,证明:GO⊥平面ACB1.题型一题型二题型三题型四(1)解:不一定成立.如例题解析在长方体ABCD-A1B1C1D1中,BD与AC不一定垂直,故BD1与平面AB1C不一定垂直,所以EF∥BD1不一定成立.
(2)证明:如图所示,连接BC1,B1D1,则B1C⊥BC1.
又D1C1⊥B1C,D1C1∩BC1=C1,∴B1C⊥平面BC1D1.
∵BD1?平面BC1D1,∴B1C⊥BD1.
∵由例题知AC⊥平面BB1D1D,且BD1?平面BB1D1D,
∴AC⊥BD1.
又AC∩B1C=C,∴BD1⊥平面ACB1.
∵由点G,O分别为DD1,DB的中点,知GO∥BD1,
∴GO⊥平面ACB1.题型一题型二题型三题型四【例3】 如图所示,P是四边形ABCD所在平面外一点,四边形ABCD是∠DAB=60°的菱形,G为AD边的中点,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
求证:(1)BG⊥平面PAD;
(2)AD⊥PB.
分析:由题干可获取以下主要信息:①四边形ABCD是∠DAB=60°的菱形;②平面PAD⊥平面ABCD.解答本题可先由面垂直于面得线垂直于面,再进一步得出线垂直于线.题型一题型二题型三题型四证明:(1)如图所示,连接PG,BD.
∵△PAD为正三角形,G是AD的中点,∴PG⊥AD.
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PG⊥平面ABCD.
∵BG?平面ABCD,∴PG⊥BG.
又四边形ABCD是菱形,且∠DAB=60°,
∴△ABD是正三角形,∴BG⊥AD.
又AD?平面PAD,PG?平面PAD,且AD∩PG=G,
∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
又BG?平面PBG,PG?平面PBG,且BG∩PG=G,
∴AD⊥平面PBG.∵PB?平面PBG,∴AD⊥PB.题型一题型二题型三题型四反思证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理,本题已知面面垂直,故考虑利用面面垂直的性质定理.利用面面垂直的性质定理证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.题型一题型二题型三题型四题型一题型二题型三题型四证明:如图所示,取CD的中点E,连接PE,EM,EA.
∵△PCD为正三角形,∴PE⊥CD,PE=
又平面PCD⊥平面ABCD,∴PE⊥平面ABCD.
又AM?平面ABCD,∴PE⊥AM.
∵四边形ABCD为矩形,
∴△ADE,△ECM,△ABM均为直角三角形,
∴EM2+AM2=AE2,即AM⊥EM.
又PE∩EM=E,∴AM⊥平面PME.∴AM⊥PM.题型一题型二题型三题型四易错点:应用定理时因忽视条件而致误
【例4】 如图所示,已知S为△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC.
求证:BC⊥AB.
错解:∵SA⊥平面ABC,且平面SAB⊥平面SBC,
∴BC⊥SB,∴BC⊥平面SAB.
又AB?平面SAB,∴BC⊥AB.
错因分析:错因是没有理解面面垂直的定理,误认为若两个平面垂直,则一个平面内的所有直线都垂直于另一个平面,显然不正确.知道面面垂直,要证线线垂直,可将证线线垂直转化为线面垂直,由已知面面垂直,则可在一个面内作两个平面的交线的垂线,由面面垂直的性质定理可知该直线垂直于另一个平面.题型一题型二题型三题型四正解:如图所示,过点A作AE⊥SB,垂足为E,
∵平面SAB⊥平面SBC,且平面SAB∩平面SBC=SB,∴AE⊥平面SBC.
∴BC⊥AE,由已知SA⊥平面ABC,得SA⊥BC,
∴BC⊥平面SAB,∴BC⊥AB.题型一题型二题型三题型四【变式训练4】 如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,PB⊥BC.求证:BC⊥PA.题型一题型二题型三题型四证明:
如图所示,作PO⊥AB,垂足为O.因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,所以PO⊥平面ABC,所以PO⊥BC.
因为PB⊥BC,PO∩PB=P,所以BC⊥平面PAB.
因为PA?平面PAB,所以BC⊥PA.1 2 3 4 51.已知直线a,b,平面α,且a⊥α,下列条件中,能推出a∥b的是( )
A.b∥α B.b?α
C.b⊥α D.b与α相交
解析:由线面垂直的性质定理可知,当b⊥α,a⊥α时,a∥b.
答案:C1 2 3 4 52.给出下列命题:
①平行于同一平面的两直线平行;
②垂直于同一平面的两直线平行;
③平行于同一直线的两平面平行;
④垂直于同一直线的两平面平行.
其中正确的有( )
A.②④ B.①②④
C.③④ D.②③④1 2 3 4 5解析:如图所示,A1B1∥平面ABCD,A1D1∥平面ABCD,而A1B1与A1D1相交,故①错误;C1C∥平面A1ABB1,C1C∥平面A1ADD1,而平面A1ABB1∩平面A1ADD1=A1A,故③错误;②④正确.故选A.
答案:A1 2 3 4 53.已知m,n是直线,α,β,γ是平面,给出下列命题:
①若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,m∥n,且n?α,n?β,则n∥α且n∥β.
其中正确命题的序号是 .?1 2 3 4 5解析:如图所示,命题①显然错误.
∵α∥β,∴α与β无公共点.
∴交线m与交线n也无公共点.
又m?γ,n?γ,∴m∥n.命题②正确.
虽然直线m不垂直于α,但m有可能垂直于平面α内的一条直线,于是α内所有平行于这条直线的无数平行直线都垂直于m.命题③错误.
由直线与平面平行的判定定理可知:
α∩β=m,∴m?α,m?β.
又m∥n,n?α,n?β,
∴必有n∥α,n∥β.命题④正确.故应填②④.
答案:②④1 2 3 4 54.已知平面α⊥平面β,α∩β=l,点P∈l,给出下面四个结论,正确的有 (只填序号).?
①过点P与l垂直的直线在α内;②过点P与β垂直的直线在α内;③过点P与l垂直的直线必与α垂直;④过点P与β垂直的平面必与l垂直.
解析:画出示意图,如图所示,显然,MP⊥l,但MP不在平面α内,故①不正确;②是面面垂直性质定理的推论,故②正确;③l可能在平面α内,故③不正确;④平面α是过P且与β垂直的平面,但l?α,而不是l⊥α,故④不正确.
答案:②1 2 3 4 55.如图所示,平面α⊥平面β,α∩β=AB,CD?β,且CD⊥AB,CE?α,EF?α,∠FEC=90°.求证:平面EFD⊥平面DCE.
证明:∵α⊥β,CD?β,CD⊥AB,α∩β=AB,
∴CD⊥α.
∵EF?α,∴CD⊥EF.
又∠FEC=90°,∴EF⊥EC.
∵EC∩CD=C,
∴EF⊥平面DCE.
又EF?平面EFD,
∴平面EFD⊥平面DCE.
2.会用两个性质定理解决相关问题.
3.理解线线垂直、线面垂直、面面垂直的内在联系.1.直线与平面垂直的性质定理 名师点拨1.利用线面垂直的性质来证明线线平行时,其关键是找出一个平面,使所证直线都与该平面垂直.
2.线面垂直的性质定理、线面平行的性质定理、平行于同一直线的两条直线平行都是证明线线平行的依据.证明线面平行、面面平行,归结到最后还是证明线线平行.
3.垂直于同一直线的两个平面互相平行.2.平面与平面垂直的性质定理 名师点拨1.应用面面垂直的性质定理时必须注意到两个条件:(1)线在平面内;(2)线垂直于两平面的交线,因此找准两平面的交线是关键.
2.已知面面垂直的条件,其性质定理就给出了作辅助线的一种方法,设法找出(作出)一个平面内的一条直线垂直于它们的交线,就可得到线面垂直的结论.【做一做】 如图所示,已知平面α⊥平面β,α∩β=b,直线a?α,且a⊥β.求证:a∥α.
证明:如图所示,在平面α内作直线c,使c⊥b.
因为α⊥β,α∩β=b,所以c⊥β.
又a⊥β,因此,a∥c.
又a?α,c?α,所以a∥α.题型一题型二题型三题型四【例1】 已知直线m,n,平面α,β,下列说法正确的是 ( )
A.m⊥α,n?β,m⊥n,则α⊥β
B.α⊥β,m⊥α,n∥β,则m⊥n
C.α∥β,m⊥α,n∥β,则m⊥n
D.α⊥β,α∩β=m,m⊥n,则n⊥β题型一题型二题型三题型四解析:如图所示,在正方体ABCD- A1B1C1D1中,直线C1C⊥平面ABCD,直线D1C1?平面A1B1C1D1,直线C1C⊥直线D1C1,但是平面ABCD与平面A1B1C1D1平行,排除A选项;平面ABCD⊥平面D1DCC1,直线C1C⊥平面ABCD,B1B∥平面D1DCC1,但是B1B∥C1C,排除B选项;平面ABCD⊥平面A1ABB1,平面ABCD∩平面A1ABB1=AB,AB⊥BC1,但是BC1不垂直于平面A1ABB1,排除D选项.
答案:C
反思本题是符号语言表述的位置关系的判断题,以选择题的形式出现,通常借助几何模型,利用排除法,排除错误的选项.题型一题型二题型三题型四【变式训练1】 已知平面α⊥平面β,m是α内一条直线,n是β内一条直线,且m⊥n,那么:①m⊥β;②n⊥α;③m⊥β或n⊥α;④m⊥β且n⊥α.这四个结论中,不正确的三个是( )
A.①②③ B.①②④
C.①③④ D.②③④
解析:本题主要考查面面垂直的性质和线面垂直的判定,解决问题的关键是正确理解定理的条件及结论.在正方体ABCD-A1B1C1D1中,令平面ABCD和平面CDD1C1分别为α和β,若m为AB,n为CC1,则m⊥n,但m∥β,故①错误;同理②④错误.故选B.
答案:B题型一题型二题型三题型四【例2】 如图所示,在正方体ABCD- A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.
求证:EF∥BD1.
分析:题目条件中给出了线线垂直,通过转化可证得线面垂直,要证EF∥BD1,只需证明EF与BD1同垂直于某一平面即可,由条件可知这里选择平面AB1C.题型一题型二题型三题型四证明:连接AB1,B1C,BD,B1D1,如图所示.
∵DD1⊥平面ABCD,AC?平面ABCD,∴DD1⊥AC.
又AC⊥BD,∴AC⊥平面BDD1B1.
∵BD1?平面BDD1B1,∴AC⊥BD1.
同理BD1⊥B1C,又AC∩B1C=C,
∴BD1⊥平面AB1C.
∵EF⊥A1D,且A1D∥B1C,∴EF⊥B1C.
又EF⊥AC,且AC ∩B1C=C,∴EF⊥平面AB1C.
∴EF∥BD1.
反思当题中垂直条件很多,但又需证明两条直线平行时,就要考虑用直线与平面垂直的性质定理,从而完成由垂直向平行的转化.题型一题型二题型三题型四【变式训练2】 (1)本例中的“正方体ABCD-A1B1C1D1”换为“长方体ABCD-A1B1C1D1”,结论“EF∥BD1”还成立吗?
(2)本例中去掉点E,点F,线段A1D,若AC与BD的交点为O,DD1的中点为G,证明:GO⊥平面ACB1.题型一题型二题型三题型四(1)解:不一定成立.如例题解析在长方体ABCD-A1B1C1D1中,BD与AC不一定垂直,故BD1与平面AB1C不一定垂直,所以EF∥BD1不一定成立.
(2)证明:如图所示,连接BC1,B1D1,则B1C⊥BC1.
又D1C1⊥B1C,D1C1∩BC1=C1,∴B1C⊥平面BC1D1.
∵BD1?平面BC1D1,∴B1C⊥BD1.
∵由例题知AC⊥平面BB1D1D,且BD1?平面BB1D1D,
∴AC⊥BD1.
又AC∩B1C=C,∴BD1⊥平面ACB1.
∵由点G,O分别为DD1,DB的中点,知GO∥BD1,
∴GO⊥平面ACB1.题型一题型二题型三题型四【例3】 如图所示,P是四边形ABCD所在平面外一点,四边形ABCD是∠DAB=60°的菱形,G为AD边的中点,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
求证:(1)BG⊥平面PAD;
(2)AD⊥PB.
分析:由题干可获取以下主要信息:①四边形ABCD是∠DAB=60°的菱形;②平面PAD⊥平面ABCD.解答本题可先由面垂直于面得线垂直于面,再进一步得出线垂直于线.题型一题型二题型三题型四证明:(1)如图所示,连接PG,BD.
∵△PAD为正三角形,G是AD的中点,∴PG⊥AD.
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PG⊥平面ABCD.
∵BG?平面ABCD,∴PG⊥BG.
又四边形ABCD是菱形,且∠DAB=60°,
∴△ABD是正三角形,∴BG⊥AD.
又AD?平面PAD,PG?平面PAD,且AD∩PG=G,
∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
又BG?平面PBG,PG?平面PBG,且BG∩PG=G,
∴AD⊥平面PBG.∵PB?平面PBG,∴AD⊥PB.题型一题型二题型三题型四反思证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理,本题已知面面垂直,故考虑利用面面垂直的性质定理.利用面面垂直的性质定理证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.题型一题型二题型三题型四题型一题型二题型三题型四证明:如图所示,取CD的中点E,连接PE,EM,EA.
∵△PCD为正三角形,∴PE⊥CD,PE=
又平面PCD⊥平面ABCD,∴PE⊥平面ABCD.
又AM?平面ABCD,∴PE⊥AM.
∵四边形ABCD为矩形,
∴△ADE,△ECM,△ABM均为直角三角形,
∴EM2+AM2=AE2,即AM⊥EM.
又PE∩EM=E,∴AM⊥平面PME.∴AM⊥PM.题型一题型二题型三题型四易错点:应用定理时因忽视条件而致误
【例4】 如图所示,已知S为△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC.
求证:BC⊥AB.
错解:∵SA⊥平面ABC,且平面SAB⊥平面SBC,
∴BC⊥SB,∴BC⊥平面SAB.
又AB?平面SAB,∴BC⊥AB.
错因分析:错因是没有理解面面垂直的定理,误认为若两个平面垂直,则一个平面内的所有直线都垂直于另一个平面,显然不正确.知道面面垂直,要证线线垂直,可将证线线垂直转化为线面垂直,由已知面面垂直,则可在一个面内作两个平面的交线的垂线,由面面垂直的性质定理可知该直线垂直于另一个平面.题型一题型二题型三题型四正解:如图所示,过点A作AE⊥SB,垂足为E,
∵平面SAB⊥平面SBC,且平面SAB∩平面SBC=SB,∴AE⊥平面SBC.
∴BC⊥AE,由已知SA⊥平面ABC,得SA⊥BC,
∴BC⊥平面SAB,∴BC⊥AB.题型一题型二题型三题型四【变式训练4】 如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,PB⊥BC.求证:BC⊥PA.题型一题型二题型三题型四证明:
如图所示,作PO⊥AB,垂足为O.因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,所以PO⊥平面ABC,所以PO⊥BC.
因为PB⊥BC,PO∩PB=P,所以BC⊥平面PAB.
因为PA?平面PAB,所以BC⊥PA.1 2 3 4 51.已知直线a,b,平面α,且a⊥α,下列条件中,能推出a∥b的是( )
A.b∥α B.b?α
C.b⊥α D.b与α相交
解析:由线面垂直的性质定理可知,当b⊥α,a⊥α时,a∥b.
答案:C1 2 3 4 52.给出下列命题:
①平行于同一平面的两直线平行;
②垂直于同一平面的两直线平行;
③平行于同一直线的两平面平行;
④垂直于同一直线的两平面平行.
其中正确的有( )
A.②④ B.①②④
C.③④ D.②③④1 2 3 4 5解析:如图所示,A1B1∥平面ABCD,A1D1∥平面ABCD,而A1B1与A1D1相交,故①错误;C1C∥平面A1ABB1,C1C∥平面A1ADD1,而平面A1ABB1∩平面A1ADD1=A1A,故③错误;②④正确.故选A.
答案:A1 2 3 4 53.已知m,n是直线,α,β,γ是平面,给出下列命题:
①若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,m∥n,且n?α,n?β,则n∥α且n∥β.
其中正确命题的序号是 .?1 2 3 4 5解析:如图所示,命题①显然错误.
∵α∥β,∴α与β无公共点.
∴交线m与交线n也无公共点.
又m?γ,n?γ,∴m∥n.命题②正确.
虽然直线m不垂直于α,但m有可能垂直于平面α内的一条直线,于是α内所有平行于这条直线的无数平行直线都垂直于m.命题③错误.
由直线与平面平行的判定定理可知:
α∩β=m,∴m?α,m?β.
又m∥n,n?α,n?β,
∴必有n∥α,n∥β.命题④正确.故应填②④.
答案:②④1 2 3 4 54.已知平面α⊥平面β,α∩β=l,点P∈l,给出下面四个结论,正确的有 (只填序号).?
①过点P与l垂直的直线在α内;②过点P与β垂直的直线在α内;③过点P与l垂直的直线必与α垂直;④过点P与β垂直的平面必与l垂直.
解析:画出示意图,如图所示,显然,MP⊥l,但MP不在平面α内,故①不正确;②是面面垂直性质定理的推论,故②正确;③l可能在平面α内,故③不正确;④平面α是过P且与β垂直的平面,但l?α,而不是l⊥α,故④不正确.
答案:②1 2 3 4 55.如图所示,平面α⊥平面β,α∩β=AB,CD?β,且CD⊥AB,CE?α,EF?α,∠FEC=90°.求证:平面EFD⊥平面DCE.
证明:∵α⊥β,CD?β,CD⊥AB,α∩β=AB,
∴CD⊥α.
∵EF?α,∴CD⊥EF.
又∠FEC=90°,∴EF⊥EC.
∵EC∩CD=C,
∴EF⊥平面DCE.
又EF?平面EFD,
∴平面EFD⊥平面DCE.
