高中数学北师大版必修2第一章立体几何初步1.7.2柱、锥、台的体积:29张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.7.2柱、锥、台的体积:29张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 928.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 21:56:53 | ||
图片预览






文档简介
课件29张PPT。7.2 柱、锥、台的体积1.掌握柱、锥、台的体积公式及求法.
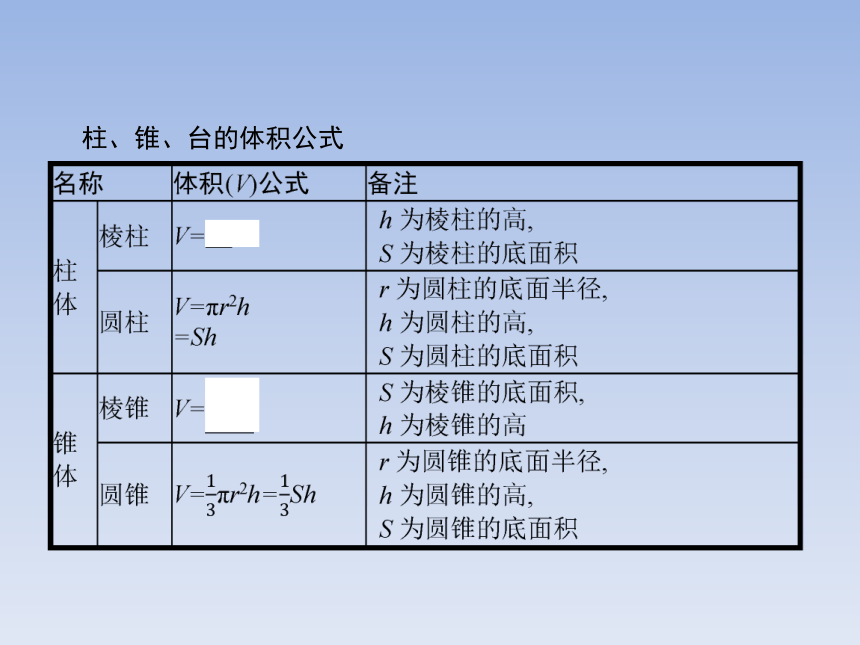
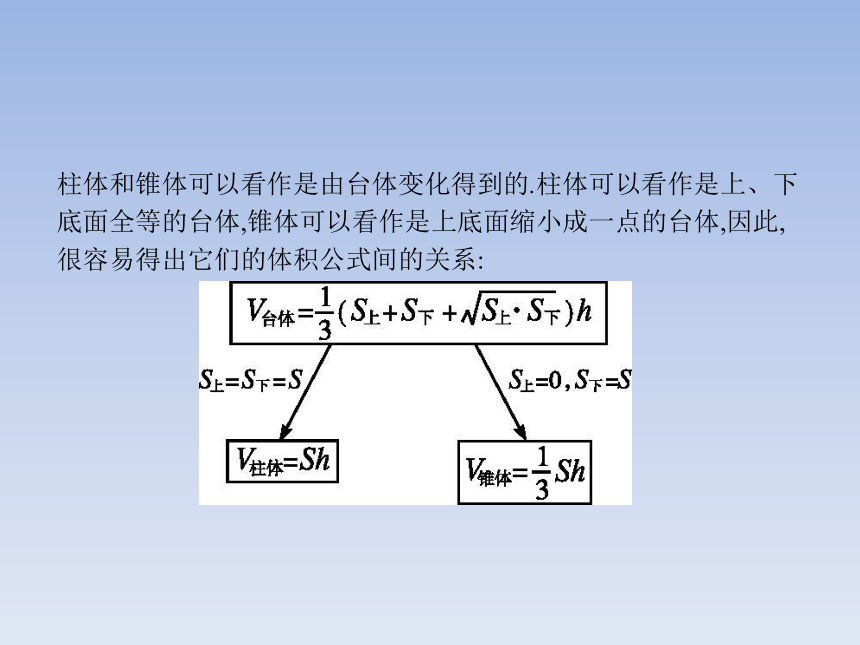
2.能运用公式求解柱体、锥体和台体的体积,并熟悉台体与柱体及锥体之间的转换关系.柱、锥、台的体积公式 柱体和锥体可以看作是由台体变化得到的.柱体可以看作是上、下底面全等的台体,锥体可以看作是上底面缩小成一点的台体,因此,很容易得出它们的体积公式间的关系: 【做一做1】 已知圆柱OO'的高为5,底面直径为4,则圆柱OO'的体积为( )
A.20 B.10 C.20π D.80π
答案:C
【做一做2】 已知五棱锥的高为10,底面积为3,则其体积为( )
A.30 B.10 C.3 D.1
答案:B
【做一做3】 已知圆锥的底面半径为1,高为2,则圆锥的体积为( )
A. B.2π C.4π D.6π
答案:A【做一做4】 已知圆台的上、下底面半径分别是2,4,高是3,则该圆台的体积是( )
答案:A
【做一做5】 在正四棱台ABCD-A'B'C'D'中,AB=2,A'B'=6,体积V=112,求该正四棱台的高.
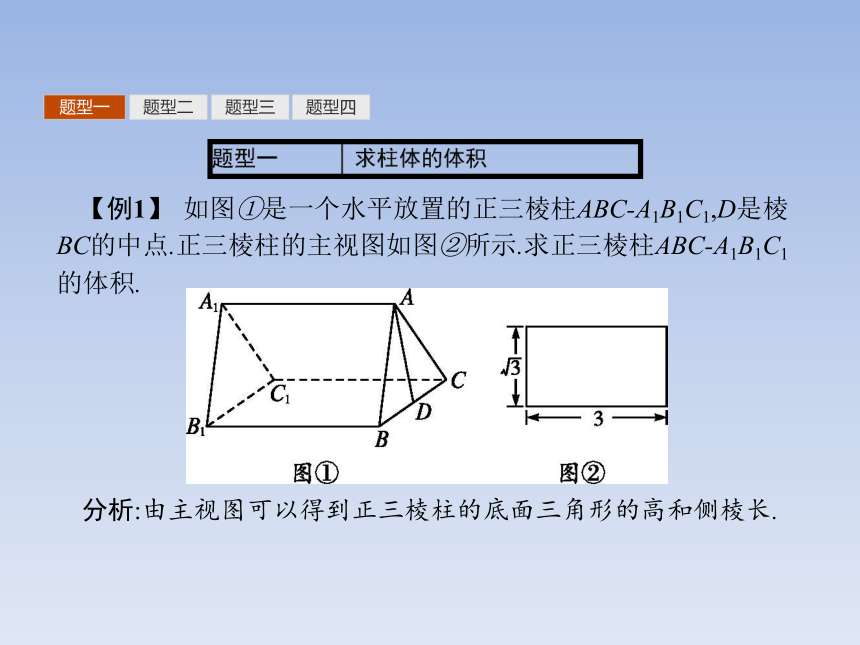
解设该正四棱台的高为h,题型一题型二题型三题型四【例1】 如图①是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②所示.求正三棱柱ABC-A1B1C1的体积.
分析:由主视图可以得到正三棱柱的底面三角形的高和侧棱长.题型一题型二题型三题型四反思求柱体的体积的关键是求底面积和高,而底面积的求解要根据平面图形的性质灵活处理.熟记常见平面图形的面积的求法是解决此类问题的关键.题型一题型二题型三题型四【变式训练1】 一个正方体和一个圆柱等高,并且侧面面积相等,则这个正方体和圆柱的体积之比为 .?
解析:由于正方体和圆柱等高,故可设正方体的棱长和圆柱的高(母线长)都为a,设圆柱的底面半径为r,
则正方体的侧面面积为4a2,圆柱的侧面面积为2πra,题型一题型二题型三题型四【例2】 一个正三棱锥的底面边长为6,侧棱长为 ,求这个正三棱锥的体积.
分析:已知底面边长和侧棱长,可先求出三棱锥的底面积和高,再根据体积公式求出其体积.题型一题型二题型三题型四题型一题型二题型三题型四反思求锥体的体积,首先要选择适当的底面和高,然后应用公式V= Sh进行计算即可,常用方法为割补法和等积变换法:
(1)割补法:求一个几何体的体积可以将这个几何体分割成几个柱体或锥体,分别求出柱体或锥体的体积,从而得出该几何体的体积.
(2)等积变换法:利用三棱锥的任一个面可作为三棱锥的底面,可通过多种方式求其体积.
①求体积时,可选择容易计算的方式来计算;
②利用“等积性”可求“点到面的距离”.题型一题型二题型三题型四【变式训练2】 两个圆锥的母线长相等,侧面展开图扇形圆心角分别为120°和240°,体积分别为V1和V2,则V1∶V2等于( )
答案:C题型一题型二题型三题型四【例3】 如图所示,已知四边形ABCD的顶点在平面直角坐标系中的坐标为A(0,0),B(1,0),C(2,1),D(0,3),将该四边形绕y轴旋转一周后,求所得旋转体的体积.
分析:该旋转体的上部是一个圆锥,下部是一个圆台,根据点B,C,D的坐标可以求出底面半径、高等关键量.题型一题型二题型三题型四题型一题型二题型三题型四【变式训练3】 已知正四棱台两底面边长分别是20和10,侧面积是780,则此正四棱台的体积是 .?题型一题型二题型三题型四答案:2 800 题型一题型二题型三题型四易错点:求几何体体积时考虑不周而致误
【例4】
如图所示,已知多面体ABCDEFG中,AB,AC,AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,求该多面体的体积.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练4】 一几何体按比例绘制的三视图,如图所示(单位:m):
(1)试画出它的直观图;
(2)求它的表面积和体积.解:(1)直观图如图所示. 题型一题型二题型三题型四1 2 3 4 51.已知一个圆柱的底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
解析:V圆柱=πr2h=π×(4÷2)2×4=16π.
答案:D1 2 3 4 52.一几何体的三视图如图所示,则该几何体的体积为( )
A.200+9π
B.200+18π
C.140+9π
D.140+18π
解析:这个几何体由上、下两部分组成,下部分是长方体,其中长、宽、高分别为6+2+2=10,1+2+1=4,5,上部分为一个横放的半圆柱,其中底面半径为3,母线长为2,故V=10×4×5+ π×32×2=200+9π.
答案:A1 2 3 4 53一正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14 cm3,则该棱台的高为 .?
答案:2 cm1 2 3 4 5答案:48 cm3 1 2 3 4 55.某几何体的三视图及其尺寸如图所示(单位:cm),求该几何体的表面积和体积. 1 2 3 4 5
2.能运用公式求解柱体、锥体和台体的体积,并熟悉台体与柱体及锥体之间的转换关系.柱、锥、台的体积公式 柱体和锥体可以看作是由台体变化得到的.柱体可以看作是上、下底面全等的台体,锥体可以看作是上底面缩小成一点的台体,因此,很容易得出它们的体积公式间的关系: 【做一做1】 已知圆柱OO'的高为5,底面直径为4,则圆柱OO'的体积为( )
A.20 B.10 C.20π D.80π
答案:C
【做一做2】 已知五棱锥的高为10,底面积为3,则其体积为( )
A.30 B.10 C.3 D.1
答案:B
【做一做3】 已知圆锥的底面半径为1,高为2,则圆锥的体积为( )
A. B.2π C.4π D.6π
答案:A【做一做4】 已知圆台的上、下底面半径分别是2,4,高是3,则该圆台的体积是( )
答案:A
【做一做5】 在正四棱台ABCD-A'B'C'D'中,AB=2,A'B'=6,体积V=112,求该正四棱台的高.
解设该正四棱台的高为h,题型一题型二题型三题型四【例1】 如图①是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②所示.求正三棱柱ABC-A1B1C1的体积.
分析:由主视图可以得到正三棱柱的底面三角形的高和侧棱长.题型一题型二题型三题型四反思求柱体的体积的关键是求底面积和高,而底面积的求解要根据平面图形的性质灵活处理.熟记常见平面图形的面积的求法是解决此类问题的关键.题型一题型二题型三题型四【变式训练1】 一个正方体和一个圆柱等高,并且侧面面积相等,则这个正方体和圆柱的体积之比为 .?
解析:由于正方体和圆柱等高,故可设正方体的棱长和圆柱的高(母线长)都为a,设圆柱的底面半径为r,
则正方体的侧面面积为4a2,圆柱的侧面面积为2πra,题型一题型二题型三题型四【例2】 一个正三棱锥的底面边长为6,侧棱长为 ,求这个正三棱锥的体积.
分析:已知底面边长和侧棱长,可先求出三棱锥的底面积和高,再根据体积公式求出其体积.题型一题型二题型三题型四题型一题型二题型三题型四反思求锥体的体积,首先要选择适当的底面和高,然后应用公式V= Sh进行计算即可,常用方法为割补法和等积变换法:
(1)割补法:求一个几何体的体积可以将这个几何体分割成几个柱体或锥体,分别求出柱体或锥体的体积,从而得出该几何体的体积.
(2)等积变换法:利用三棱锥的任一个面可作为三棱锥的底面,可通过多种方式求其体积.
①求体积时,可选择容易计算的方式来计算;
②利用“等积性”可求“点到面的距离”.题型一题型二题型三题型四【变式训练2】 两个圆锥的母线长相等,侧面展开图扇形圆心角分别为120°和240°,体积分别为V1和V2,则V1∶V2等于( )
答案:C题型一题型二题型三题型四【例3】 如图所示,已知四边形ABCD的顶点在平面直角坐标系中的坐标为A(0,0),B(1,0),C(2,1),D(0,3),将该四边形绕y轴旋转一周后,求所得旋转体的体积.
分析:该旋转体的上部是一个圆锥,下部是一个圆台,根据点B,C,D的坐标可以求出底面半径、高等关键量.题型一题型二题型三题型四题型一题型二题型三题型四【变式训练3】 已知正四棱台两底面边长分别是20和10,侧面积是780,则此正四棱台的体积是 .?题型一题型二题型三题型四答案:2 800 题型一题型二题型三题型四易错点:求几何体体积时考虑不周而致误
【例4】
如图所示,已知多面体ABCDEFG中,AB,AC,AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,求该多面体的体积.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练4】 一几何体按比例绘制的三视图,如图所示(单位:m):
(1)试画出它的直观图;
(2)求它的表面积和体积.解:(1)直观图如图所示. 题型一题型二题型三题型四1 2 3 4 51.已知一个圆柱的底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
解析:V圆柱=πr2h=π×(4÷2)2×4=16π.
答案:D1 2 3 4 52.一几何体的三视图如图所示,则该几何体的体积为( )
A.200+9π
B.200+18π
C.140+9π
D.140+18π
解析:这个几何体由上、下两部分组成,下部分是长方体,其中长、宽、高分别为6+2+2=10,1+2+1=4,5,上部分为一个横放的半圆柱,其中底面半径为3,母线长为2,故V=10×4×5+ π×32×2=200+9π.
答案:A1 2 3 4 53一正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14 cm3,则该棱台的高为 .?
答案:2 cm1 2 3 4 5答案:48 cm3 1 2 3 4 55.某几何体的三视图及其尺寸如图所示(单位:cm),求该几何体的表面积和体积. 1 2 3 4 5
