高中数学北师大版必修2第一章立体几何初步1.7.3球:24张PPT
文档属性
| 名称 | 高中数学北师大版必修2第一章立体几何初步1.7.3球:24张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 00:00:00 | ||
图片预览







文档简介
课件24张PPT。7.3 球1.理解球的截面,并能解决相关问题.
2.了解圆的切线的相关概念,记住球的表面积和体积公式.
3.会用球的表面积公式和体积公式进行有关计算,并能解决一些简单的实际问题.1.球的截面
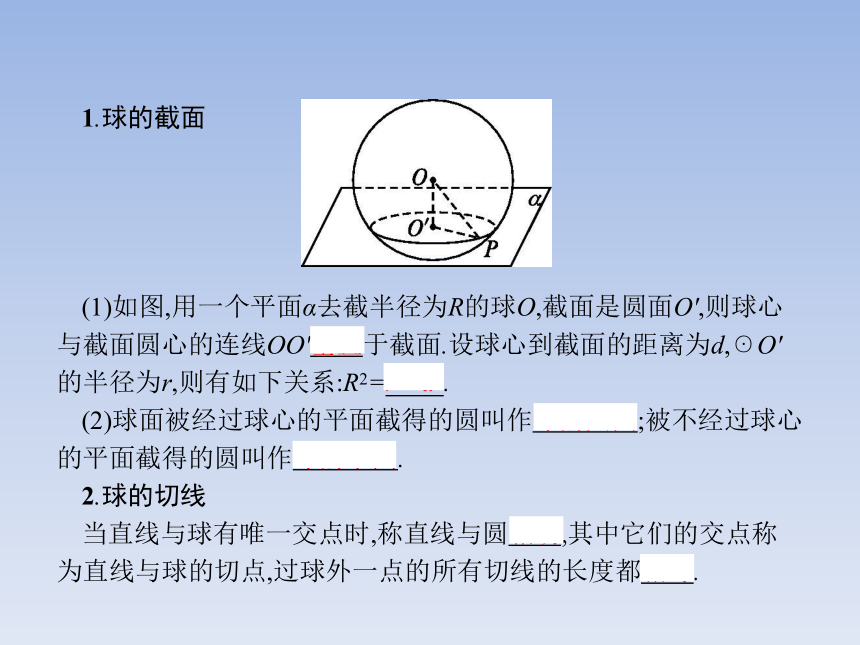
(1)如图,用一个平面α去截半径为R的球O,截面是圆面O',则球心与截面圆心的连线OO'垂直于截面.设球心到截面的距离为d,☉O'的半径为r,则有如下关系:R2=r2+d2.
(2)球面被经过球心的平面截得的圆叫作球的大圆;被不经过球心的平面截得的圆叫作球的小圆.
2.球的切线
当直线与球有唯一交点时,称直线与圆相切,其中它们的交点称为直线与球的切点,过球外一点的所有切线的长度都相等.3.球的体积
4.球的表面积
设球的半径为R,那么它的表面积S=4πR2.
说明:(1)球的表面积和体积公式均是关于球的半径的函数.
(2)球的表面不像柱体、锥体和台体那样可以展开在一个平面上,即使是球面上任意小的一块,也不能展开在一个平面上,因此球的表面没有展开图.【做一做1】 直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
答案:D
【做一做2】 8个半径为1的铁球,熔化成一个大球,则大球的表面积是 .?
答案:16π【做一做3】 过球的某一条半径的中点,作一个垂直于这条半径的截面,截面面积为48π cm2,求球的表面积.题型一题型二题型三题型四【例1】 在球内有相距为1的两个平行截面,截面面积分别是5π和8π,球心不在两截面之间,求球的表面积.
分析:求球的表面积或体积只需要求出球的半径,要求球的半径只需解球的半径、截面圆半径和球心到截面的距离组成的直角三角形.题型一题型二题型三题型四解:设球的半径为R,过截面圆圆心作垂直于截面的球的轴截面(过轴的截面),如图所示.圆O是圆心在球心的圆,A1B1,A2B2分别是两个平行截面圆的直径.过圆心O作OC1垂直A1B1于点C1,并延长交A2B2于点C2.因为A1B1∥A2B2,所以OC2⊥A2B2.
由圆的性质可得,C1和C2分别是A1B1和A2B2的中点.题型一题型二题型三题型四反思球的轴截面(过球心的截面)是将球的问题转化为圆的问题的关键,因此必须抓住球的轴截面,利用其性质列出方程(组),求球的半径,进而解决问题.题型一题型二题型三题型四【变式训练1】 三个球的半径之比为1∶2∶3,则最大球的表面积是其余两个球的表面积之和的( )
答案:C题型一题型二题型三题型四反思计算球的体积或体积的简单应用都需要认真解决球的半径问题.题型一题型二题型三题型四【变式训练2】 一个平面截一球得到直径为6 cm的圆面,球心到这个截面的距离为4 cm,则球的体积为 .?
解析:如图所示,由已知,O1A=3 cm,OO1=4 cm,
∴R=OA=5 cm,题型一题型二题型三题型四【例3】 在球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的体积.
分析:因为PA,PB,PC是两两互相垂直且相等的三条棱,所以可以将三棱锥P-ABC看成一个正方体的一角,P,A,B,C四点在球面上,所以此球可视为以PA,PB,PC为相邻三条棱的正方体的外接球,其直径为正方体的体对角线.题型一题型二题型三题型四解:设球的半径为R,因为PA,PB,PC两两互相垂直,且PA=PB=PC=a,
所以以PA,PB,PC为相邻三条棱可以构造正方体.又因为P,A,B,C是球面上的四点,
所以球是所构造的正方体的外接球,正方体的体对角线是球的直径,反思与球有关的组合体问题,通常有两种情况:一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.球与旋转体的组合,通常作它们的轴截面,球与多面体的组合,通常通过多面体的一条侧棱和球心,或“切点”“接点”作出截面图.题型一题型二题型三题型四【变式训练3】 有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
解:设正方体的棱长为a.
①正方体的内切球球心是正方体的中心,切点是六个正方形的中心,经过四个切点及球心作截面,如图甲,所以有2r1=a,题型一题型二题型三题型四题型一题型二题型三题型四易错点:考虑问题不全而致误
【例4】 一个球内有相距9 cm的两个平行截面,面积分别为49π cm2和400π cm2,求球的表面积.
错解:
如图所示,设OD=xcm,由题意知π·CA2=49π,
∴CA=7 cm.又π·BD2=400π,∴BD=20 cm.
设球的半径为Rcm,则有(CD+DO)2+CA2=R2=OD2+DB2,即(9+x)2+72=x2+202,∴x=15,R=25.∴S球=4πR2=2 500π cm2.
错因分析:本题出现错解的原因在于考虑不周,由于球心可能在两个截面之间,也可能在两个截面的同一侧,因此解决此题要分类讨论.题型一题型二题型三题型四正解:(1)当球心在两个截面的同侧时,解法同错解.
(2)
当球心在两个截面之间时,如图所示,设OD=x,则OC=9-x.
设球的半径为R,
可得x2+202=(9-x)2+72=R2,
此方程无正数解,即此种情况不可能.
综上可知,球的表面积是2 500π cm2.题型一题型二题型三题型四【变式训练4】 设球O的半径为5,一个内接圆台的两底面半径分别是3和4,求圆台的体积.
解:如图所示,分两种情况,1 2 3 4 5答案:B 1 2 3 4 52.如果两个球的半径之比为1∶3,那么这两个球的表面积之比为( )
A.1∶9 B.1∶27 C.1∶3 D.1∶1
解析:设两个球的半径分别为R1,R2,
答案:A1 2 3 4 53.两个球的表面积之差为48π,它们的大圆周长之和为12π,则这两个球的半径之差为( )
A.4 B.3 C.2 D.1
解析:设两个球的半径分别为R,r(R>r).由题意,知
答案:C1 2 3 4 54.一个正四棱柱的各个顶点在一个直径为2 cm的球面上,如果正四棱柱的底面边长为1 cm,那么该正四棱柱的侧面积为 .?1 2 3 4 55.某个几何体的三视图如图所示(单位:m).
求:(1)该几何体的表面积(结果保留π);
(2)该几何体的体积(结果保留π).1 2 3 4 5
2.了解圆的切线的相关概念,记住球的表面积和体积公式.
3.会用球的表面积公式和体积公式进行有关计算,并能解决一些简单的实际问题.1.球的截面
(1)如图,用一个平面α去截半径为R的球O,截面是圆面O',则球心与截面圆心的连线OO'垂直于截面.设球心到截面的距离为d,☉O'的半径为r,则有如下关系:R2=r2+d2.
(2)球面被经过球心的平面截得的圆叫作球的大圆;被不经过球心的平面截得的圆叫作球的小圆.
2.球的切线
当直线与球有唯一交点时,称直线与圆相切,其中它们的交点称为直线与球的切点,过球外一点的所有切线的长度都相等.3.球的体积
4.球的表面积
设球的半径为R,那么它的表面积S=4πR2.
说明:(1)球的表面积和体积公式均是关于球的半径的函数.
(2)球的表面不像柱体、锥体和台体那样可以展开在一个平面上,即使是球面上任意小的一块,也不能展开在一个平面上,因此球的表面没有展开图.【做一做1】 直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
答案:D
【做一做2】 8个半径为1的铁球,熔化成一个大球,则大球的表面积是 .?
答案:16π【做一做3】 过球的某一条半径的中点,作一个垂直于这条半径的截面,截面面积为48π cm2,求球的表面积.题型一题型二题型三题型四【例1】 在球内有相距为1的两个平行截面,截面面积分别是5π和8π,球心不在两截面之间,求球的表面积.
分析:求球的表面积或体积只需要求出球的半径,要求球的半径只需解球的半径、截面圆半径和球心到截面的距离组成的直角三角形.题型一题型二题型三题型四解:设球的半径为R,过截面圆圆心作垂直于截面的球的轴截面(过轴的截面),如图所示.圆O是圆心在球心的圆,A1B1,A2B2分别是两个平行截面圆的直径.过圆心O作OC1垂直A1B1于点C1,并延长交A2B2于点C2.因为A1B1∥A2B2,所以OC2⊥A2B2.
由圆的性质可得,C1和C2分别是A1B1和A2B2的中点.题型一题型二题型三题型四反思球的轴截面(过球心的截面)是将球的问题转化为圆的问题的关键,因此必须抓住球的轴截面,利用其性质列出方程(组),求球的半径,进而解决问题.题型一题型二题型三题型四【变式训练1】 三个球的半径之比为1∶2∶3,则最大球的表面积是其余两个球的表面积之和的( )
答案:C题型一题型二题型三题型四反思计算球的体积或体积的简单应用都需要认真解决球的半径问题.题型一题型二题型三题型四【变式训练2】 一个平面截一球得到直径为6 cm的圆面,球心到这个截面的距离为4 cm,则球的体积为 .?
解析:如图所示,由已知,O1A=3 cm,OO1=4 cm,
∴R=OA=5 cm,题型一题型二题型三题型四【例3】 在球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的体积.
分析:因为PA,PB,PC是两两互相垂直且相等的三条棱,所以可以将三棱锥P-ABC看成一个正方体的一角,P,A,B,C四点在球面上,所以此球可视为以PA,PB,PC为相邻三条棱的正方体的外接球,其直径为正方体的体对角线.题型一题型二题型三题型四解:设球的半径为R,因为PA,PB,PC两两互相垂直,且PA=PB=PC=a,
所以以PA,PB,PC为相邻三条棱可以构造正方体.又因为P,A,B,C是球面上的四点,
所以球是所构造的正方体的外接球,正方体的体对角线是球的直径,反思与球有关的组合体问题,通常有两种情况:一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.球与旋转体的组合,通常作它们的轴截面,球与多面体的组合,通常通过多面体的一条侧棱和球心,或“切点”“接点”作出截面图.题型一题型二题型三题型四【变式训练3】 有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
解:设正方体的棱长为a.
①正方体的内切球球心是正方体的中心,切点是六个正方形的中心,经过四个切点及球心作截面,如图甲,所以有2r1=a,题型一题型二题型三题型四题型一题型二题型三题型四易错点:考虑问题不全而致误
【例4】 一个球内有相距9 cm的两个平行截面,面积分别为49π cm2和400π cm2,求球的表面积.
错解:
如图所示,设OD=xcm,由题意知π·CA2=49π,
∴CA=7 cm.又π·BD2=400π,∴BD=20 cm.
设球的半径为Rcm,则有(CD+DO)2+CA2=R2=OD2+DB2,即(9+x)2+72=x2+202,∴x=15,R=25.∴S球=4πR2=2 500π cm2.
错因分析:本题出现错解的原因在于考虑不周,由于球心可能在两个截面之间,也可能在两个截面的同一侧,因此解决此题要分类讨论.题型一题型二题型三题型四正解:(1)当球心在两个截面的同侧时,解法同错解.
(2)
当球心在两个截面之间时,如图所示,设OD=x,则OC=9-x.
设球的半径为R,
可得x2+202=(9-x)2+72=R2,
此方程无正数解,即此种情况不可能.
综上可知,球的表面积是2 500π cm2.题型一题型二题型三题型四【变式训练4】 设球O的半径为5,一个内接圆台的两底面半径分别是3和4,求圆台的体积.
解:如图所示,分两种情况,1 2 3 4 5答案:B 1 2 3 4 52.如果两个球的半径之比为1∶3,那么这两个球的表面积之比为( )
A.1∶9 B.1∶27 C.1∶3 D.1∶1
解析:设两个球的半径分别为R1,R2,
答案:A1 2 3 4 53.两个球的表面积之差为48π,它们的大圆周长之和为12π,则这两个球的半径之差为( )
A.4 B.3 C.2 D.1
解析:设两个球的半径分别为R,r(R>r).由题意,知
答案:C1 2 3 4 54.一个正四棱柱的各个顶点在一个直径为2 cm的球面上,如果正四棱柱的底面边长为1 cm,那么该正四棱柱的侧面积为 .?1 2 3 4 55.某个几何体的三视图如图所示(单位:m).
求:(1)该几何体的表面积(结果保留π);
(2)该几何体的体积(结果保留π).1 2 3 4 5
