2019版物理新教材人教版必修一同步练习:实验探究弹簧弹力与形变量的关系(解析版)
文档属性
| 名称 | 2019版物理新教材人教版必修一同步练习:实验探究弹簧弹力与形变量的关系(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-10-12 19:57:33 | ||
图片预览


文档简介
2019版物理新教材人教版必修一同步练习:实验探究弹簧弹力与形变量的关系(word解析版)
1.某同学在探究弹力和弹簧伸长的关系,并测定弹簧的劲度系数。
主要实验步骤如下:将待测弹簧的一端固定在铁架台上,然后将毫米刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好指在刻度尺上。当弹簧自然下垂时,指针的指示值记作;弹簧下端挂一个砝码时,指针的指示值记作;弹簧下端挂两个砝码时,指针的指示值记作……;挂七个砝码时,指针的位置如图所示,指针的指示值记作。
已知每个砝码的质量均为50g;测量记录表:
(1)实验中,的值还未读出,请你根据上图将这个测量值填入记录表中_________。
(2)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了四个差值:,,,。根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长量。用、、、表示的式?子为_________________。
(3)计算弹簧的劲度系数__________。(取9.8)
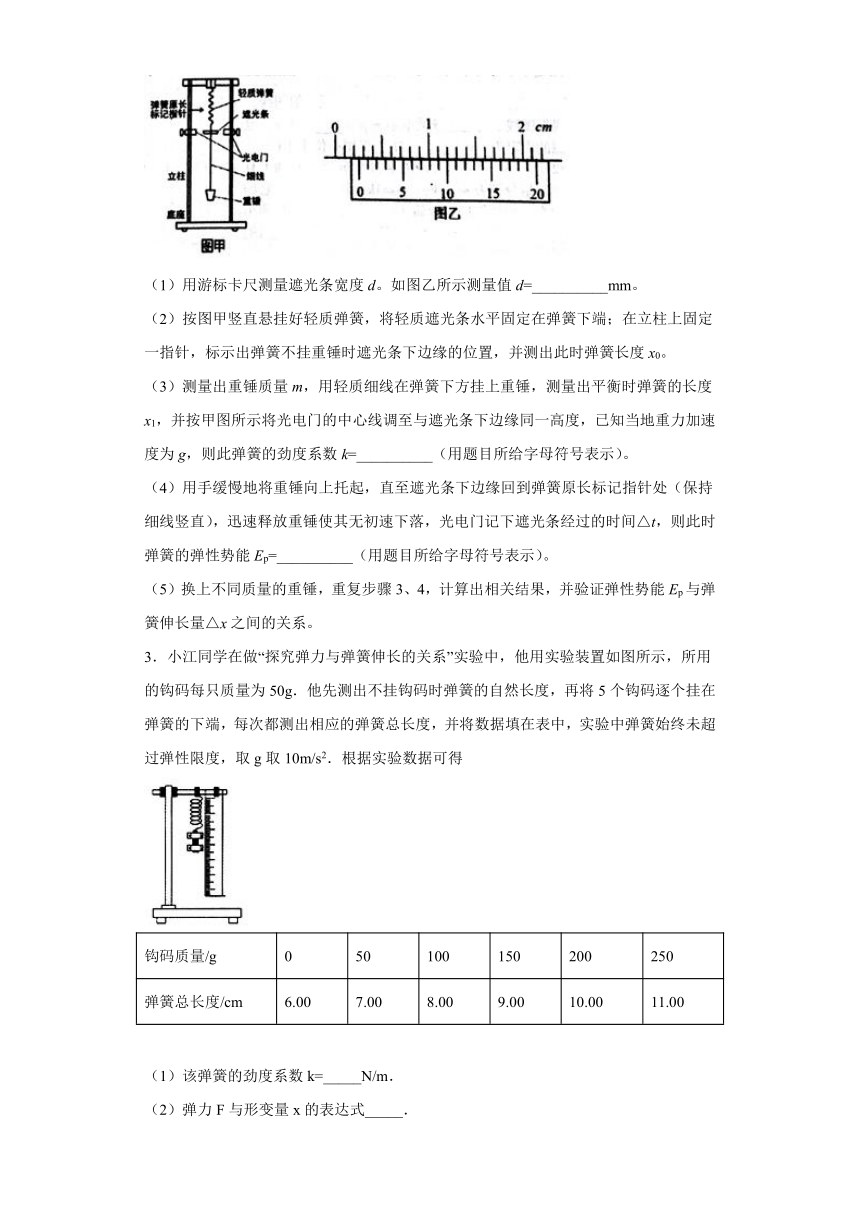
2.某同学利用如图甲装置探究弹簧的弹性势能EP与弹簧伸长量Δx之间的关系。实验步骤如下:
(1)用游标卡尺测量遮光条宽度d。如图乙所示测量值d=__________mm。
(2)按图甲竖直悬挂好轻质弹簧,将轻质遮光条水平固定在弹簧下端;在立柱上固定一指针,标示出弹簧不挂重锤时遮光条下边缘的位置,并测出此时弹簧长度x0。
(3)测量出重锤质量m,用轻质细线在弹簧下方挂上重锤,测量出平衡时弹簧的长度x1,并按甲图所示将光电门的中心线调至与遮光条下边缘同一高度,已知当地重力加速度为g,则此弹簧的劲度系数k=__________(用题目所给字母符号表示)。
(4)用手缓慢地将重锤向上托起,直至遮光条下边缘回到弹簧原长标记指针处(保持细线竖直),迅速释放重锤使其无初速下落,光电门记下遮光条经过的时间△t,则此时弹簧的弹性势能Ep=__________(用题目所给字母符号表示)。
(5)换上不同质量的重锤,重复步骤3、4,计算出相关结果,并验证弹性势能Ep与弹簧伸长量△x之间的关系。
3.小江同学在做“探究弹力与弹簧伸长的关系”实验中,他用实验装置如图所示,所用的钩码每只质量为50g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在表中,实验中弹簧始终未超过弹性限度,取g取10m/s2.根据实验数据可得
钩码质量/g
0
50
100
150
200
250
弹簧总长度/cm
6.00
7.00
8.00
9.00
10.00
11.00
(1)该弹簧的劲度系数k=_____N/m.
(2)弹力F与形变量x的表达式_____.
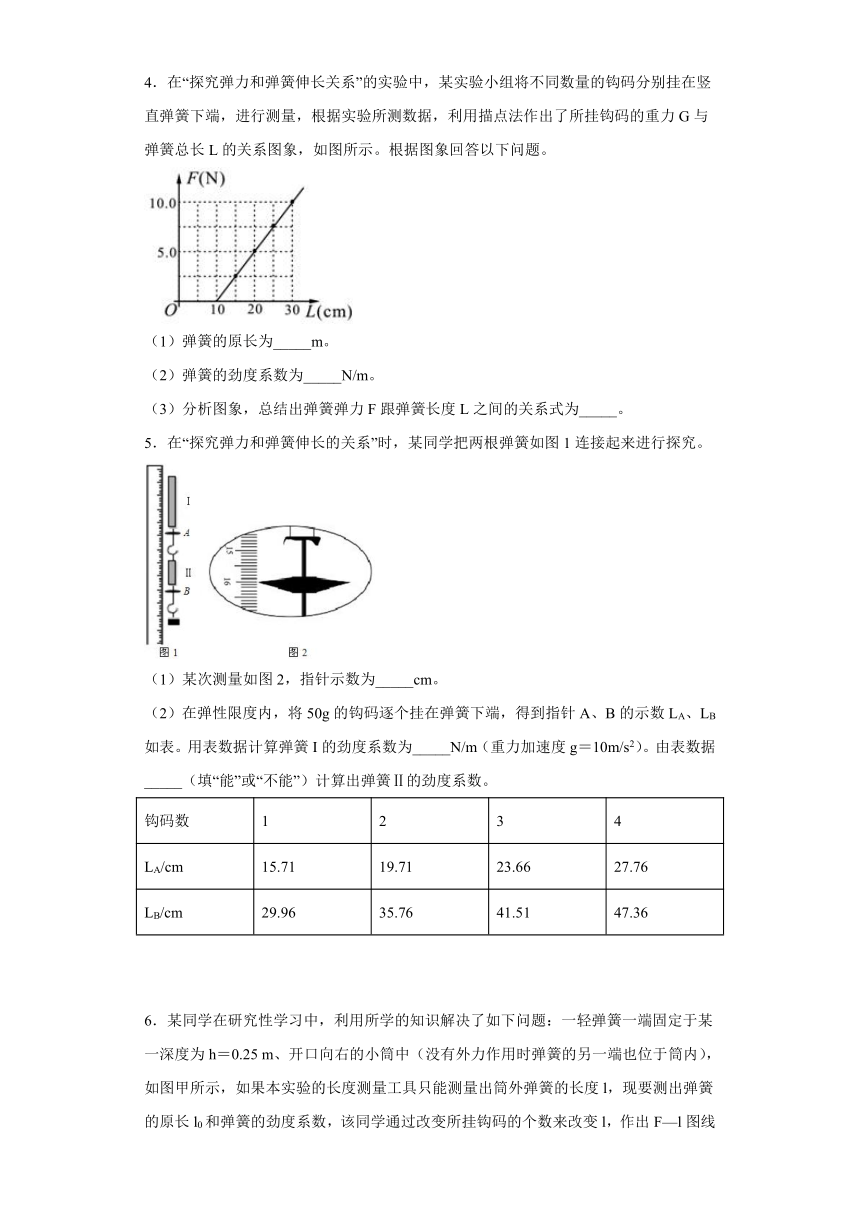
4.在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示。根据图象回答以下问题。
(1)弹簧的原长为_____m。
(2)弹簧的劲度系数为_____N/m。
(3)分析图象,总结出弹簧弹力F跟弹簧长度L之间的关系式为_____。
5.在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如图1连接起来进行探究。
(1)某次测量如图2,指针示数为_____cm。
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA、LB如表。用表数据计算弹簧I的劲度系数为_____N/m(重力加速度g=10m/s2)。由表数据_____(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数。
钩码数
1
2
3
4
LA/cm
15.71
19.71
23.66
27.76
LB/cm
29.96
35.76
41.51
47.36
6.某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧一端固定于某一深度为h=0.25 m、开口向右的小筒中(没有外力作用时弹簧的另一端也位于筒内),如图甲所示,如果本实验的长度测量工具只能测量出筒外弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数,该同学通过改变所挂钩码的个数来改变l,作出F—l图线如图乙所示。
(1)由此图线可得出的结论是____________。
(2)弹簧的劲度系数为_______N/m,弹簧的原长l0=_______m.
7.为了探究弹力F与弹簧伸长量x的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为________________。甲、乙两根弹簧的劲度系数分别为:________N/m、________N/m。若要制作一个精确度较高的弹簧测力计,应选弹簧________(填“甲”或“乙”)。
8.某同学探究弹力与弹簧伸长量的关系.
(1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧.弹簧轴线和刻度尺都应在________方向(填“水平”或“竖直”).
(2)弹簧自然悬挂,待弹簧静止时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6,数据如下表.
表中有一个数值记录不规范,代表符号为________.
(3)下图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与________的差值(填“L0”或“Lx”).
(4)由图可知弹簧的劲度系数为________N/m;通过图和表可知砝码盘的质量为________g.(结果保留两位有效数字,重力加速度取9.8 m/s2)
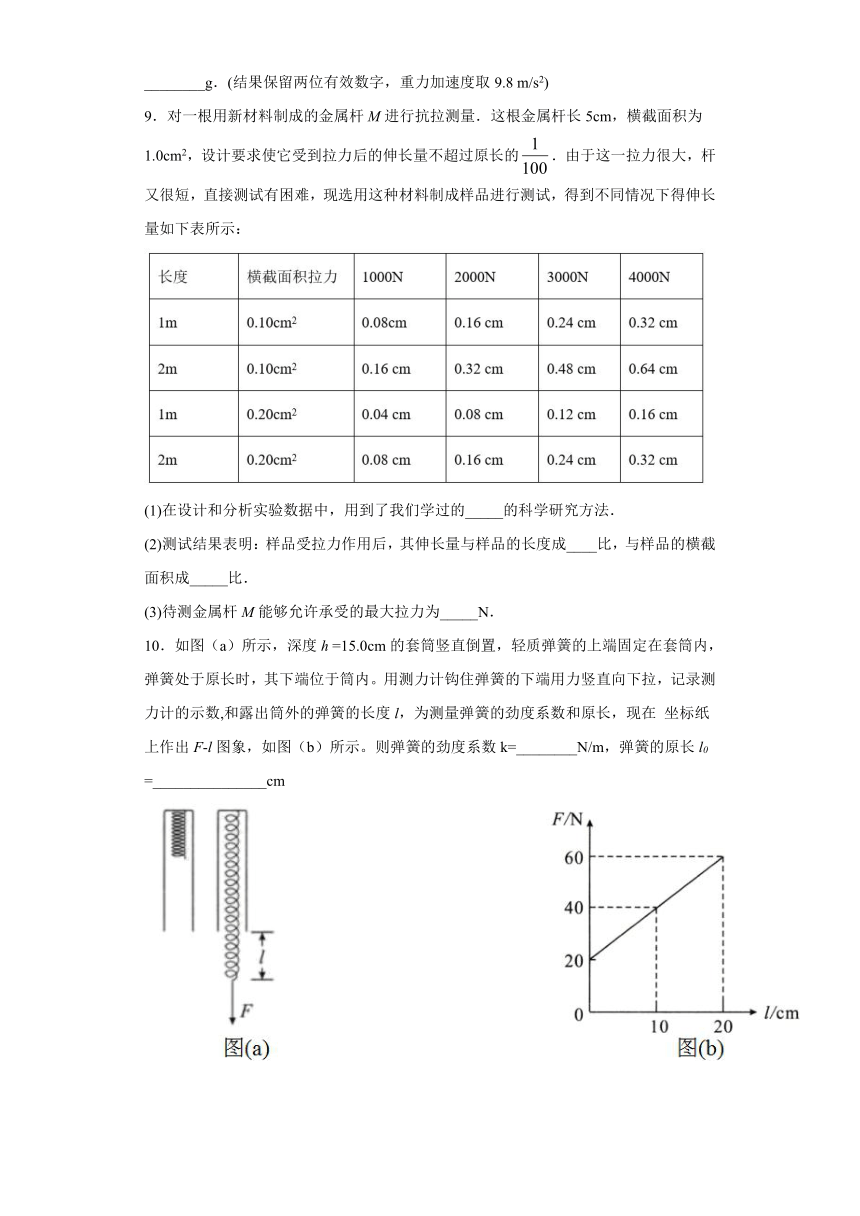
9.对一根用新材料制成的金属杆M进行抗拉测量.这根金属杆长5cm,横截面积为1.0cm2,设计要求使它受到拉力后的伸长量不超过原长的.由于这一拉力很大,杆又很短,直接测试有困难,现选用这种材料制成样品进行测试,得到不同情况下得伸长量如下表所示:
(1)在设计和分析实验数据中,用到了我们学过的_____的科学研究方法.
(2)测试结果表明:样品受拉力作用后,其伸长量与样品的长度成____比,与样品的横截面积成_____比.
(3)待测金属杆M能够允许承受的最大拉力为_____N.
10.如图(a)所示,深度h =15.0cm的套筒竖直倒置,轻质弹簧的上端固定在套筒内,弹簧处于原长时,其下端位于筒内。用测力计钩住弹簧的下端用力竖直向下拉,记录测力计的示数,和露出筒外的弹簧的长度l,为测量弹簧的劲度系数和原长,现在 坐标纸上作出F-l图象,如图(b)所示。则弹簧的劲度系数k=________N/m,弹簧的原长l0 =_______________cm
参考答案
1.14.05 (14.03~14.07) 28
【解析】
【详解】
(1)[1]毫米刻度尺的最小分度值为1mm,估读到0.1mm,L7的读数为14.05cm .
(2)[2]根据各个差值,可以求出每增加50g砝码的弹簧平均伸长量△L,△L用d1、d2、d3、d4表示的式子为
(3)[3]据,有:
根据胡克定律有
m0g=
利用数据可求得
2.2.50
【解析】
【详解】
(1)[1]游标卡尺的读数为;
(3)[2]根据胡克定律可知,解得;
(4)[3]此时重物的速度为,根据动能定理可知
,
解得
.
3.50 F=50x
【解析】
(1)根据F=kx可知,
(2)弹力F与形变量x的表达式F=50x
【点睛】对于该实验要注意:每次增减砝码测量有关长度时,均要保证弹簧及砝码应处于静止状态.测量有关长度时,要注意区分弹簧的原长l0,实际长度l和伸长量x,并明确三者之间的关系.
4.10 1000
【解析】
【分析】
根据题意可知,弹簧总长度L(cm)与所挂物体重力G(N)之间符合一次函数关系,根据胡克定律写出F与L的方程即可正确解答.
【详解】
(1)当弹簧下端所挂钩码的重力G为0时,弹簧的拉力也为0,此时弹簧长度即为原长,由图示图象可知,弹簧的原长为:0.10m.
(2)由图示图象可知,弹簧的劲度系数为.
(3)由图示图象可知,弹簧力F跟弹簧长度L之间的关系式为:
F=k(L﹣L0)=1000(L﹣10)×0.01=10(L﹣10).
【点睛】
本题比较简单,结合图象考查了胡克定律的基础知识,是一道考查基础知识的好题.在研究弹簧的伸长与拉力的关系问题时,一定要特别区分“弹簧的长度”与“弹簧的伸长”的不同.
5.(1)16.00;(2)12.5,能
【解析】
【分析】
(1)刻度尺的读数需估读,需读到最小刻度的下一位.(2)根据弹簧Ⅰ形变量的变化量,结合胡克定律求出劲度系数.通过弹簧Ⅱ弹力的变化量和形变量的变化量可以求出弹簧Ⅱ的劲度系数.
【详解】
(1)刻度尺读数需读到最小刻度的下一位,指针示数为16.00cm.
(2)由表格中的数据可知,当弹力的变化量△F=0.5N时,弹簧形变量的变化量为△x=4.00cm,根据胡克定律知:,结合L1和L2示数的变化,可以得出弹簧Ⅱ形变量的变化量,结合弹力变化量,根据胡克定律能求出弹簧Ⅱ的劲度系数.
【点睛】
解决本题的关键掌握胡克定律,知道F=kx,x表示形变量,以及知道其变形式△F=k△x,△x为形变量的变化量.
6.在弹性限度内,弹力与弹簧的伸长量成正比 100 0.15
【解析】
【详解】
试题分析:(1)[1] 根据图象结合数学知识可知:在弹性限度内,弹力与弹簧的伸长量成正比;
(2)[2][3]根据胡克定律F与的关系式为:
,
从图象中可得直线的斜率为2N/cm,截距为20N,故弹簧的劲度系数为
,
由
,
于是:
考点:考查了胡可定律
【名师点睛】
找到各个物理量之间的关系,然后根据胡克定律列方程,是解答本题的突破口,这要求学生有较强的数学推导能力.
7.超过弹簧的弹性限度; 66.7; 200; 甲;
【解析】
【详解】
根据胡克定律,在弹性限度内,弹簧的弹力与行变量成正比,故F﹣x图是直线,向上弯曲的原因是超出了弹性限度,注意该图象中纵坐标为伸长量,横坐标为拉力,斜率的倒数为劲度系数,由此可求出kA=66.7N/m,kB=200N/m,由于甲的劲度系数小,因此其精度高.
故答案为:超过弹簧的弹性限度,66.7,200,甲.
【点评】
本题考查了弹簧弹力F和弹簧伸长量x的关系的基础知识,比较简单,是一道考查基础知识的好题.
8.竖直 L3 Lx 4.9 10
【解析】
【详解】
(1)[1].将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧.弹簧轴线和刻度尺都应在竖直方向.
(2)[2].用毫米刻度尺测量长度是要估读到分度值的下一位,故L3的数值记录不规范;
(3)[3].在砝码盘中每次增加10g砝码,所以弹簧的形变量应该是弹簧长度与LX的差值. (4)[4]. 根据胡克定律公式△F=k△x,有
[5].通过图和表可知:L0=25.35cm,Lx=27.35cm 所以砝码盘的质量为:
9.控制变量法 正 反 125000
【解析】
【详解】
(1)[1]由题可知伸长量x与样品的长度、横截面积、所受拉力都有关系,涉及的变量较多,因此采用“控制变量法”来确定它们之间的正、反比关系.
(2)[2][3]由表格知:
①、当受到的拉力F、横截面积S一定时,伸长量x与样品长度L成正比,
②、当受到的拉力F、样品长度L一定时,伸长量x与横截面积S成反比,
③、当样品长度L、横截面积S一定时,伸长量x与受到的拉力F成正比,
综上得,样品受拉力作用后,其伸长量与样品的长度成正比,与样品的横截面积成反比.
(3)[4]由上面结论,可以归纳出,x与L、S、F之间存在一定量的比例关系,设这个比值为k,那么有:线材伸长量x与材料的长度L、材料的横截面积S与拉力F的函数关系为
(k为常数)
则:
取S=0.10cm2=1.0×10-5m2,x=0.08cm=8×10-4m,L=1m,F=1000N,则:
k=8.0×10-12m2/N
将金属杆长5cm=0.05m,横截面积为1.0cm2=1×10-4m2,设计要求使它受到拉力后的伸长量不超过原长的,代入公式得:
F=125000N.
10.200 5.0
【解析】
【详解】
[1] [2]根据胡克定律F与l的关系式为:
F=k(l+h-l0)=kl+k(h-l0),
从图象中可得直线的斜率为2N/cm,截距为20N,故弹簧的劲度系数为:
k=2N/cm=200N/m
由
k(h-l0)=20N
解得:
l0=5.0cm
1.某同学在探究弹力和弹簧伸长的关系,并测定弹簧的劲度系数。
主要实验步骤如下:将待测弹簧的一端固定在铁架台上,然后将毫米刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好指在刻度尺上。当弹簧自然下垂时,指针的指示值记作;弹簧下端挂一个砝码时,指针的指示值记作;弹簧下端挂两个砝码时,指针的指示值记作……;挂七个砝码时,指针的位置如图所示,指针的指示值记作。
已知每个砝码的质量均为50g;测量记录表:
(1)实验中,的值还未读出,请你根据上图将这个测量值填入记录表中_________。
(2)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了四个差值:,,,。根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长量。用、、、表示的式?子为_________________。
(3)计算弹簧的劲度系数__________。(取9.8)
2.某同学利用如图甲装置探究弹簧的弹性势能EP与弹簧伸长量Δx之间的关系。实验步骤如下:
(1)用游标卡尺测量遮光条宽度d。如图乙所示测量值d=__________mm。
(2)按图甲竖直悬挂好轻质弹簧,将轻质遮光条水平固定在弹簧下端;在立柱上固定一指针,标示出弹簧不挂重锤时遮光条下边缘的位置,并测出此时弹簧长度x0。
(3)测量出重锤质量m,用轻质细线在弹簧下方挂上重锤,测量出平衡时弹簧的长度x1,并按甲图所示将光电门的中心线调至与遮光条下边缘同一高度,已知当地重力加速度为g,则此弹簧的劲度系数k=__________(用题目所给字母符号表示)。
(4)用手缓慢地将重锤向上托起,直至遮光条下边缘回到弹簧原长标记指针处(保持细线竖直),迅速释放重锤使其无初速下落,光电门记下遮光条经过的时间△t,则此时弹簧的弹性势能Ep=__________(用题目所给字母符号表示)。
(5)换上不同质量的重锤,重复步骤3、4,计算出相关结果,并验证弹性势能Ep与弹簧伸长量△x之间的关系。
3.小江同学在做“探究弹力与弹簧伸长的关系”实验中,他用实验装置如图所示,所用的钩码每只质量为50g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在表中,实验中弹簧始终未超过弹性限度,取g取10m/s2.根据实验数据可得
钩码质量/g
0
50
100
150
200
250
弹簧总长度/cm
6.00
7.00
8.00
9.00
10.00
11.00
(1)该弹簧的劲度系数k=_____N/m.
(2)弹力F与形变量x的表达式_____.
4.在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示。根据图象回答以下问题。
(1)弹簧的原长为_____m。
(2)弹簧的劲度系数为_____N/m。
(3)分析图象,总结出弹簧弹力F跟弹簧长度L之间的关系式为_____。
5.在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如图1连接起来进行探究。
(1)某次测量如图2,指针示数为_____cm。
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA、LB如表。用表数据计算弹簧I的劲度系数为_____N/m(重力加速度g=10m/s2)。由表数据_____(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数。
钩码数
1
2
3
4
LA/cm
15.71
19.71
23.66
27.76
LB/cm
29.96
35.76
41.51
47.36
6.某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧一端固定于某一深度为h=0.25 m、开口向右的小筒中(没有外力作用时弹簧的另一端也位于筒内),如图甲所示,如果本实验的长度测量工具只能测量出筒外弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数,该同学通过改变所挂钩码的个数来改变l,作出F—l图线如图乙所示。
(1)由此图线可得出的结论是____________。
(2)弹簧的劲度系数为_______N/m,弹簧的原长l0=_______m.
7.为了探究弹力F与弹簧伸长量x的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为________________。甲、乙两根弹簧的劲度系数分别为:________N/m、________N/m。若要制作一个精确度较高的弹簧测力计,应选弹簧________(填“甲”或“乙”)。
8.某同学探究弹力与弹簧伸长量的关系.
(1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧.弹簧轴线和刻度尺都应在________方向(填“水平”或“竖直”).
(2)弹簧自然悬挂,待弹簧静止时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6,数据如下表.
表中有一个数值记录不规范,代表符号为________.
(3)下图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与________的差值(填“L0”或“Lx”).
(4)由图可知弹簧的劲度系数为________N/m;通过图和表可知砝码盘的质量为________g.(结果保留两位有效数字,重力加速度取9.8 m/s2)
9.对一根用新材料制成的金属杆M进行抗拉测量.这根金属杆长5cm,横截面积为1.0cm2,设计要求使它受到拉力后的伸长量不超过原长的.由于这一拉力很大,杆又很短,直接测试有困难,现选用这种材料制成样品进行测试,得到不同情况下得伸长量如下表所示:
(1)在设计和分析实验数据中,用到了我们学过的_____的科学研究方法.
(2)测试结果表明:样品受拉力作用后,其伸长量与样品的长度成____比,与样品的横截面积成_____比.
(3)待测金属杆M能够允许承受的最大拉力为_____N.
10.如图(a)所示,深度h =15.0cm的套筒竖直倒置,轻质弹簧的上端固定在套筒内,弹簧处于原长时,其下端位于筒内。用测力计钩住弹簧的下端用力竖直向下拉,记录测力计的示数,和露出筒外的弹簧的长度l,为测量弹簧的劲度系数和原长,现在 坐标纸上作出F-l图象,如图(b)所示。则弹簧的劲度系数k=________N/m,弹簧的原长l0 =_______________cm
参考答案
1.14.05 (14.03~14.07) 28
【解析】
【详解】
(1)[1]毫米刻度尺的最小分度值为1mm,估读到0.1mm,L7的读数为14.05cm .
(2)[2]根据各个差值,可以求出每增加50g砝码的弹簧平均伸长量△L,△L用d1、d2、d3、d4表示的式子为
(3)[3]据,有:
根据胡克定律有
m0g=
利用数据可求得
2.2.50
【解析】
【详解】
(1)[1]游标卡尺的读数为;
(3)[2]根据胡克定律可知,解得;
(4)[3]此时重物的速度为,根据动能定理可知
,
解得
.
3.50 F=50x
【解析】
(1)根据F=kx可知,
(2)弹力F与形变量x的表达式F=50x
【点睛】对于该实验要注意:每次增减砝码测量有关长度时,均要保证弹簧及砝码应处于静止状态.测量有关长度时,要注意区分弹簧的原长l0,实际长度l和伸长量x,并明确三者之间的关系.
4.10 1000
【解析】
【分析】
根据题意可知,弹簧总长度L(cm)与所挂物体重力G(N)之间符合一次函数关系,根据胡克定律写出F与L的方程即可正确解答.
【详解】
(1)当弹簧下端所挂钩码的重力G为0时,弹簧的拉力也为0,此时弹簧长度即为原长,由图示图象可知,弹簧的原长为:0.10m.
(2)由图示图象可知,弹簧的劲度系数为.
(3)由图示图象可知,弹簧力F跟弹簧长度L之间的关系式为:
F=k(L﹣L0)=1000(L﹣10)×0.01=10(L﹣10).
【点睛】
本题比较简单,结合图象考查了胡克定律的基础知识,是一道考查基础知识的好题.在研究弹簧的伸长与拉力的关系问题时,一定要特别区分“弹簧的长度”与“弹簧的伸长”的不同.
5.(1)16.00;(2)12.5,能
【解析】
【分析】
(1)刻度尺的读数需估读,需读到最小刻度的下一位.(2)根据弹簧Ⅰ形变量的变化量,结合胡克定律求出劲度系数.通过弹簧Ⅱ弹力的变化量和形变量的变化量可以求出弹簧Ⅱ的劲度系数.
【详解】
(1)刻度尺读数需读到最小刻度的下一位,指针示数为16.00cm.
(2)由表格中的数据可知,当弹力的变化量△F=0.5N时,弹簧形变量的变化量为△x=4.00cm,根据胡克定律知:,结合L1和L2示数的变化,可以得出弹簧Ⅱ形变量的变化量,结合弹力变化量,根据胡克定律能求出弹簧Ⅱ的劲度系数.
【点睛】
解决本题的关键掌握胡克定律,知道F=kx,x表示形变量,以及知道其变形式△F=k△x,△x为形变量的变化量.
6.在弹性限度内,弹力与弹簧的伸长量成正比 100 0.15
【解析】
【详解】
试题分析:(1)[1] 根据图象结合数学知识可知:在弹性限度内,弹力与弹簧的伸长量成正比;
(2)[2][3]根据胡克定律F与的关系式为:
,
从图象中可得直线的斜率为2N/cm,截距为20N,故弹簧的劲度系数为
,
由
,
于是:
考点:考查了胡可定律
【名师点睛】
找到各个物理量之间的关系,然后根据胡克定律列方程,是解答本题的突破口,这要求学生有较强的数学推导能力.
7.超过弹簧的弹性限度; 66.7; 200; 甲;
【解析】
【详解】
根据胡克定律,在弹性限度内,弹簧的弹力与行变量成正比,故F﹣x图是直线,向上弯曲的原因是超出了弹性限度,注意该图象中纵坐标为伸长量,横坐标为拉力,斜率的倒数为劲度系数,由此可求出kA=66.7N/m,kB=200N/m,由于甲的劲度系数小,因此其精度高.
故答案为:超过弹簧的弹性限度,66.7,200,甲.
【点评】
本题考查了弹簧弹力F和弹簧伸长量x的关系的基础知识,比较简单,是一道考查基础知识的好题.
8.竖直 L3 Lx 4.9 10
【解析】
【详解】
(1)[1].将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧.弹簧轴线和刻度尺都应在竖直方向.
(2)[2].用毫米刻度尺测量长度是要估读到分度值的下一位,故L3的数值记录不规范;
(3)[3].在砝码盘中每次增加10g砝码,所以弹簧的形变量应该是弹簧长度与LX的差值. (4)[4]. 根据胡克定律公式△F=k△x,有
[5].通过图和表可知:L0=25.35cm,Lx=27.35cm 所以砝码盘的质量为:
9.控制变量法 正 反 125000
【解析】
【详解】
(1)[1]由题可知伸长量x与样品的长度、横截面积、所受拉力都有关系,涉及的变量较多,因此采用“控制变量法”来确定它们之间的正、反比关系.
(2)[2][3]由表格知:
①、当受到的拉力F、横截面积S一定时,伸长量x与样品长度L成正比,
②、当受到的拉力F、样品长度L一定时,伸长量x与横截面积S成反比,
③、当样品长度L、横截面积S一定时,伸长量x与受到的拉力F成正比,
综上得,样品受拉力作用后,其伸长量与样品的长度成正比,与样品的横截面积成反比.
(3)[4]由上面结论,可以归纳出,x与L、S、F之间存在一定量的比例关系,设这个比值为k,那么有:线材伸长量x与材料的长度L、材料的横截面积S与拉力F的函数关系为
(k为常数)
则:
取S=0.10cm2=1.0×10-5m2,x=0.08cm=8×10-4m,L=1m,F=1000N,则:
k=8.0×10-12m2/N
将金属杆长5cm=0.05m,横截面积为1.0cm2=1×10-4m2,设计要求使它受到拉力后的伸长量不超过原长的,代入公式得:
F=125000N.
10.200 5.0
【解析】
【详解】
[1] [2]根据胡克定律F与l的关系式为:
F=k(l+h-l0)=kl+k(h-l0),
从图象中可得直线的斜率为2N/cm,截距为20N,故弹簧的劲度系数为:
k=2N/cm=200N/m
由
k(h-l0)=20N
解得:
l0=5.0cm
