2.3.1-2.3.2空间直角坐标系的建立:33张PPT
文档属性
| 名称 | 2.3.1-2.3.2空间直角坐标系的建立:33张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 744.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 00:00:00 | ||
图片预览











文档简介
课件33张PPT。§3 空间直角坐标系3.1 空间直角坐标系的建立
3.2 空间直角坐标系中点的坐标1.了解空间直角坐标系,会利用空间直角坐标系表示点的位置.
2.利用空间直角坐标系求关于点、线、面的对称点的坐标.1.空间直角坐标系
(1)定义:在平面直角坐标系的基础上,通过原点O,再增加一条与xOy平面垂直的z轴,这样就建立了三个维度的空间直角坐标系,其中点O叫作原点,x,y,z轴统称为坐标轴,由坐标轴确定的平面叫作坐标平面.
(2)画法:在平面上画空间直角坐标系时,一般使∠xOy=135°(或45°),∠yOz=90°.
名师点拨本书建立的坐标系都是右手直角坐标系,即伸出右手,让四指与大拇指垂直,并使四指先指向x轴正方向,然后让四指沿握拳方向旋转90°指向y轴正方向,此时大拇指的指向即为z轴正向.也称这个坐标系为右手系.【做一做1】 下面表示空间直角坐标系的直观图中,是右手系的是( )
A.①③ B.③ C.①② D.①②③
答案:C2.空间直角坐标系中点的坐标
在空间直角坐标系中,用一个三元有序数组来刻画空间点的位置.空间任意一点P的坐标记为(x,y,z),第一个是x坐标,第二个是y坐标,第三个是z坐标.
在空间直角坐标系中,对于空间任意一点P,都可以用一个三元有序数组(x,y,z)来表示;反之,任何一个三元有序数组(x,y,z),都可以确定空间中的一个点P.这样,在空间直角坐标系中,点与三元有序数组之间就建立了一一对应的关系.空间中两点P1(x1,y1,z1),P2(x2,y2,z2),线段P1P2的中点为P0(x0,y0,z0),
这个公式称为空间直角坐标系中的中点坐标公式,是平面直角坐标系中中点坐标公式的拓展.【做一做2-1】 点P(2,0,3)在空间直角坐标系中的位置是在( )
A.y轴上 B.xOy平面上
C.xOz平面上 D.yOz平面上
答案:C
【做一做2-2】 在空间直角坐标系中,x轴上的点的坐标可记为( )
A.(0,b,0) B.(a,0,0)
C.(0,0,c) D.(0,b,c)
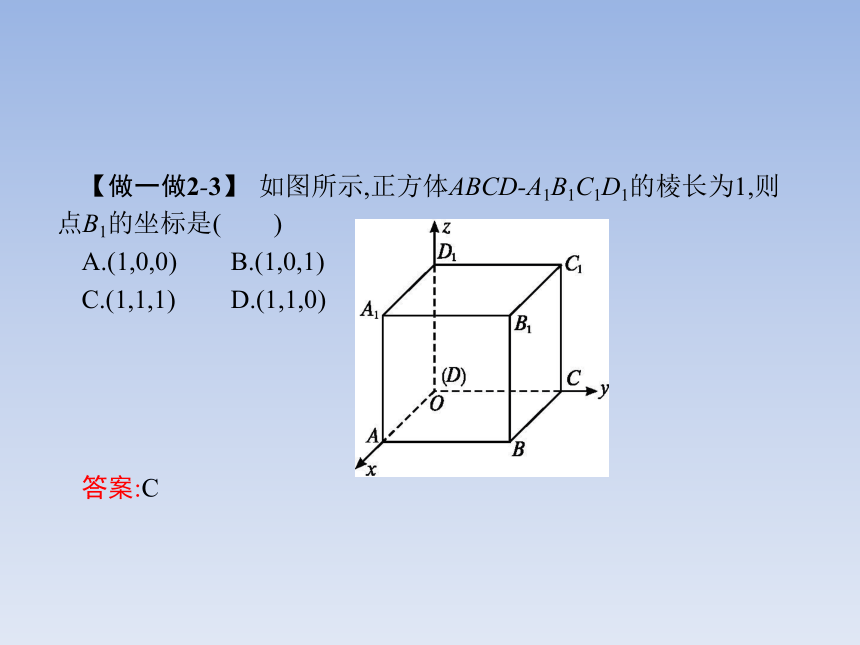
答案:B【做一做2-3】 如图所示,正方体ABCD-A1B1C1D1的棱长为1,则点B1的坐标是( )
A.(1,0,0) B.(1,0,1)
C.(1,1,1) D.(1,1,0)
答案:C题型一题型二题型三题型四【例1】 在空间直角坐标系中,作出点M(4,-2,5).
解:方法一:依据平移的方法,为了作出点M(4,-2,5),可以按如下步骤进行:
(1)在x轴上取横坐标为4的点M1;
(2)将M1在xOy平面内沿与y轴平行的方向
向左平移2个单位长度,得到点M2;
(3)将点M2沿与z轴平行的方向向上平移
5个单位长度,即可得到点M,如图所示.题型一题型二题型三题型四方法二:以O为一个顶点,构造三条棱长分别为4,2,5的长方体,使此长方体在点O处的三条棱分别在x轴的正半轴、y轴的负半轴、z轴的正半轴上,则长方体中与顶点O相对的顶点即为所求的点M,图示略.
方法三:在x轴上找到横坐标为4的点,过此点作与x轴垂直的平面α;在y轴上找到纵坐标为-2的点,过此点作与y轴垂直的平面β;在z轴上找到竖坐标为5的点,过此点作与z轴垂直的平面γ;则平面α,β,γ交于一点,此交点即为所求的点M,图示略.题型一题型二题型三题型四反思1.若要作的点M(x0,y0,z0)的坐标有两个为0,则此点是坐标轴上的点,可直接在坐标轴上作出此点.
2.若要作的点M(x0,y0,z0)的坐标有且只有一个为0,则此点不在坐标轴上,但在某一坐标平面内,可以按照类似于平面直角坐标系中作点的方法作出此点.
3.若要作的点M(x0,y0,z0)的坐标都不为0,则需要按照一定的步骤作出该点,一般有三种方法:
(1)先在x轴上取横坐标为x0的点M1;再将M1在xOy平面内沿与y轴平行的方向向左(y0<0)或向右(y0>0)平移|y0|个单位长度,得到点M2;再将点M2沿与z轴平行的方向向上(z0>0)或向下(z0<0)平移|z0|个单位长度,即可得到点M(x0,y0,z0).题型一题型二题型三题型四(2)以原点O为一个顶点,构造棱长分别为|x0|,|y0|,|z0|的长方体(三条棱的位置要与x0,y0,z0的符号一致),则长方体中与顶点O相对的顶点即为所求的点M.
(3)先在x轴上找到点M1(x0,0,0),过点M1作与x轴垂直的平面α,再在y轴上找到点M2(0,y0,0),过点M2作与y轴垂直的平面β,在z轴上找到点M3(0,0,z0),过点M3作与z轴垂直的平面γ,三个平面α,β,γ交于一点,此交点即为所求的点M.题型一题型二题型三题型四【变式训练1】 在空间直角坐标系中,作出下列各点:
A(-2,4,4),B(3,-4,2),C(4,0,-3).
解:A(-2,4,4),B(3,-4,2),C(4,0,-3)的位置如图所示.题型一题型二题型三题型四【例2】 如图所示,在长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;
(2)求点N的坐标.题型一题型二题型三题型四解:(1)显然A(0,0,0),因为点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理可得D(0,3,0),A1(0,0,5).
由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理可得B1(4,0,5),D1(0,3,5),与点C的坐标相比,点C1的坐标中只有竖坐标与点C不同,|CC1|=|AA1|=5,
则点C1(4,3,5).题型一题型二题型三题型四反思建立空间直角坐标系要把握以下原则:尽可能选取互相垂直的三个平面的交点为原点,尽可能多地把点放在坐标平面或坐标轴上.在长方体中,通常以长方体的一个顶点为原点,以这个顶点上的三条棱所在的直线为坐标轴,建立空间直角坐标系.题型一题型二题型三题型四【变式训练2】 在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点,棱长为1,建立适当的空间直角坐标系,并求点E,F的坐标.题型一题型二题型三题型四题型一题型二题型三题型四【例3】 如图所示,正方体ABCD-A1B1C1D1的棱长为a.
(1)求点B1关于平面xOy对称的点的坐标;
(2)求点B1关于z轴对称的点的坐标;
(3)求点B1关于原点对称的点的坐标.
分析:坐标系已经给出,解答本题只需先求出点B1的坐标,在此基础上借助点关于点、线、平面的对称原则求解即可.题型一题型二题型三题型四解:∵正方体ABCD-A1B1C1D1的棱长为a,
∴易求得点B1的坐标为(a,a,a).
(1)点B1关于平面xOy对称的点的坐标为(a,a,-a);
(2)点B1关于z轴对称的点的坐标为(-a,-a,a);
(3)点B1关于原点对称的点的坐标为(-a,-a,-a).题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练3】 在空间直角坐标系中,点P(-2,1,4)关于x轴对称的点的坐标是 ;关于xOy平面对称的点的坐标是 ;关于点A(1,0,2)对称的点的坐标是 .?题型一题型二题型三题型四解析:点P关于x轴对称后,它在x轴的分量不变,在y轴,z轴上的分量变为原来的相反数,所以点P关于x轴的对称点P1的坐标为(-2,-1,-4).
点P关于xOy平面对称后,它在x轴,y轴上的分量均不变,在z轴上的分量变为原来的相反数,
所以点P关于xOy平面的对称点P2的坐标为(-2,1,-4).
设点P关于点A的对称点的坐标为P3(x,y,z),由中点坐标公式可得
故点P关于点A(1,0,2)对称的点P3的坐标为(4,-1,0).
答案:(-2,-1,-4) (-2,1,-4) (4,-1,0)题型一题型二题型三题型四易错点:由于建系不当而致误
【例4】 正三棱柱ABC-A1B1C1各棱长均为1,建立正确的坐标系求点B的坐标时,下列建系方式正确的有( )
(1)以A1为原点,在平面A1B1C1内作A1C1的垂线为x轴,A1C1和AA1所在直线为y轴和z轴建立空间直角坐标系;
(2)以A为原点,分别以AB,AC,A1A所在直线为x轴、y轴、z轴建立空间直角坐标系;
(3)以A1为原点,分别以A1B1,A1C1,A1A所在直线为x轴、y轴、z轴建立空间直角坐标系;
(4)取AC的中点O和A1C1的中点O1,可得BO⊥AC,以O为原点,分别以OB,OC,OO1所在直线为x轴、y轴、z轴建立空间直角坐标系.
A.(2)(3) B.(2)(4) C.(1)(4) D.(3)(4)题型一题型二题型三题型四错解:选A或B或D
错因分析:将(2)(3)误认为x轴和y轴垂直,实际上在正三棱柱ABC-A1B1C1中,∠BAC=∠B1A1C1=60°,所以(2)(3)中的x轴与y轴不垂直,不符合空间直角坐标系的建系要求.
正解:在空间直角坐标系中,三个坐标轴的位置关系是两两互相垂直,(2)(3)中x轴和y轴不垂直,(1)(4)中三个坐标轴两两互相垂直.故选C.
答案:C题型一题型二题型三题型四【变式训练4】 在直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,∠BAC=90°,M是CC1的中点,Q是BC的中点,试建立空间直角坐标系,写出点B,C,C1,M,Q的坐标.
解:因建系不同,所得各点坐标也不同,如以A为原点,分别以AB,AC,AA1所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示,则B(2,0,0),C(0,2,0),C1(0,2,2),M(0,2,1),Q(1,1,0).1 2 3 4 51.设A(2,-3,-1),B(4,7,1),则线段AB的中点在空间直角坐标系中的位置是( )
A.在y轴上 B.在xOy面内
C.在xOz面内 D.在yOz面内
解析:根据中点坐标公式可知,AB的中点坐标为P(3,2,0),故点P在xOy面内.
答案:B1 2 3 4 5答案:D 1 2 3 4 53.已知点A(-3,1,-4),则点A关于原点的对称点A'的坐标为( )
A.(1,-3,-4) B.(-4,1,-3)
C.(3,-1,4) D.(4,-1,3)
答案:C1 2 3 4 54.在空间直角坐标系中,点M(-2,4,-3)在xOz平面上的射影为M',则M'关于原点的对称点是 .?
解析:点M在xOz平面上的射影M'的坐标为(-2,0,-3),M'关于原点的对称点为(2,0,3).
答案:(2,0,3)1 2 3 4 55.在棱长为a的正方体ABCD-A1B1C1D1中,已知B1的坐标为(a,a,a),试写出其余各顶点的坐标.
解:由B1的坐标可知,以顶点D为原点,以棱DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,由正方体的棱长为a可得D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),A1(a,0,a),C1(0,a,a),D1(0,0,a).
2.利用空间直角坐标系求关于点、线、面的对称点的坐标.1.空间直角坐标系
(1)定义:在平面直角坐标系的基础上,通过原点O,再增加一条与xOy平面垂直的z轴,这样就建立了三个维度的空间直角坐标系,其中点O叫作原点,x,y,z轴统称为坐标轴,由坐标轴确定的平面叫作坐标平面.
(2)画法:在平面上画空间直角坐标系时,一般使∠xOy=135°(或45°),∠yOz=90°.
名师点拨本书建立的坐标系都是右手直角坐标系,即伸出右手,让四指与大拇指垂直,并使四指先指向x轴正方向,然后让四指沿握拳方向旋转90°指向y轴正方向,此时大拇指的指向即为z轴正向.也称这个坐标系为右手系.【做一做1】 下面表示空间直角坐标系的直观图中,是右手系的是( )
A.①③ B.③ C.①② D.①②③
答案:C2.空间直角坐标系中点的坐标
在空间直角坐标系中,用一个三元有序数组来刻画空间点的位置.空间任意一点P的坐标记为(x,y,z),第一个是x坐标,第二个是y坐标,第三个是z坐标.
在空间直角坐标系中,对于空间任意一点P,都可以用一个三元有序数组(x,y,z)来表示;反之,任何一个三元有序数组(x,y,z),都可以确定空间中的一个点P.这样,在空间直角坐标系中,点与三元有序数组之间就建立了一一对应的关系.空间中两点P1(x1,y1,z1),P2(x2,y2,z2),线段P1P2的中点为P0(x0,y0,z0),
这个公式称为空间直角坐标系中的中点坐标公式,是平面直角坐标系中中点坐标公式的拓展.【做一做2-1】 点P(2,0,3)在空间直角坐标系中的位置是在( )
A.y轴上 B.xOy平面上
C.xOz平面上 D.yOz平面上
答案:C
【做一做2-2】 在空间直角坐标系中,x轴上的点的坐标可记为( )
A.(0,b,0) B.(a,0,0)
C.(0,0,c) D.(0,b,c)
答案:B【做一做2-3】 如图所示,正方体ABCD-A1B1C1D1的棱长为1,则点B1的坐标是( )
A.(1,0,0) B.(1,0,1)
C.(1,1,1) D.(1,1,0)
答案:C题型一题型二题型三题型四【例1】 在空间直角坐标系中,作出点M(4,-2,5).
解:方法一:依据平移的方法,为了作出点M(4,-2,5),可以按如下步骤进行:
(1)在x轴上取横坐标为4的点M1;
(2)将M1在xOy平面内沿与y轴平行的方向
向左平移2个单位长度,得到点M2;
(3)将点M2沿与z轴平行的方向向上平移
5个单位长度,即可得到点M,如图所示.题型一题型二题型三题型四方法二:以O为一个顶点,构造三条棱长分别为4,2,5的长方体,使此长方体在点O处的三条棱分别在x轴的正半轴、y轴的负半轴、z轴的正半轴上,则长方体中与顶点O相对的顶点即为所求的点M,图示略.
方法三:在x轴上找到横坐标为4的点,过此点作与x轴垂直的平面α;在y轴上找到纵坐标为-2的点,过此点作与y轴垂直的平面β;在z轴上找到竖坐标为5的点,过此点作与z轴垂直的平面γ;则平面α,β,γ交于一点,此交点即为所求的点M,图示略.题型一题型二题型三题型四反思1.若要作的点M(x0,y0,z0)的坐标有两个为0,则此点是坐标轴上的点,可直接在坐标轴上作出此点.
2.若要作的点M(x0,y0,z0)的坐标有且只有一个为0,则此点不在坐标轴上,但在某一坐标平面内,可以按照类似于平面直角坐标系中作点的方法作出此点.
3.若要作的点M(x0,y0,z0)的坐标都不为0,则需要按照一定的步骤作出该点,一般有三种方法:
(1)先在x轴上取横坐标为x0的点M1;再将M1在xOy平面内沿与y轴平行的方向向左(y0<0)或向右(y0>0)平移|y0|个单位长度,得到点M2;再将点M2沿与z轴平行的方向向上(z0>0)或向下(z0<0)平移|z0|个单位长度,即可得到点M(x0,y0,z0).题型一题型二题型三题型四(2)以原点O为一个顶点,构造棱长分别为|x0|,|y0|,|z0|的长方体(三条棱的位置要与x0,y0,z0的符号一致),则长方体中与顶点O相对的顶点即为所求的点M.
(3)先在x轴上找到点M1(x0,0,0),过点M1作与x轴垂直的平面α,再在y轴上找到点M2(0,y0,0),过点M2作与y轴垂直的平面β,在z轴上找到点M3(0,0,z0),过点M3作与z轴垂直的平面γ,三个平面α,β,γ交于一点,此交点即为所求的点M.题型一题型二题型三题型四【变式训练1】 在空间直角坐标系中,作出下列各点:
A(-2,4,4),B(3,-4,2),C(4,0,-3).
解:A(-2,4,4),B(3,-4,2),C(4,0,-3)的位置如图所示.题型一题型二题型三题型四【例2】 如图所示,在长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;
(2)求点N的坐标.题型一题型二题型三题型四解:(1)显然A(0,0,0),因为点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理可得D(0,3,0),A1(0,0,5).
由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理可得B1(4,0,5),D1(0,3,5),与点C的坐标相比,点C1的坐标中只有竖坐标与点C不同,|CC1|=|AA1|=5,
则点C1(4,3,5).题型一题型二题型三题型四反思建立空间直角坐标系要把握以下原则:尽可能选取互相垂直的三个平面的交点为原点,尽可能多地把点放在坐标平面或坐标轴上.在长方体中,通常以长方体的一个顶点为原点,以这个顶点上的三条棱所在的直线为坐标轴,建立空间直角坐标系.题型一题型二题型三题型四【变式训练2】 在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点,棱长为1,建立适当的空间直角坐标系,并求点E,F的坐标.题型一题型二题型三题型四题型一题型二题型三题型四【例3】 如图所示,正方体ABCD-A1B1C1D1的棱长为a.
(1)求点B1关于平面xOy对称的点的坐标;
(2)求点B1关于z轴对称的点的坐标;
(3)求点B1关于原点对称的点的坐标.
分析:坐标系已经给出,解答本题只需先求出点B1的坐标,在此基础上借助点关于点、线、平面的对称原则求解即可.题型一题型二题型三题型四解:∵正方体ABCD-A1B1C1D1的棱长为a,
∴易求得点B1的坐标为(a,a,a).
(1)点B1关于平面xOy对称的点的坐标为(a,a,-a);
(2)点B1关于z轴对称的点的坐标为(-a,-a,a);
(3)点B1关于原点对称的点的坐标为(-a,-a,-a).题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练3】 在空间直角坐标系中,点P(-2,1,4)关于x轴对称的点的坐标是 ;关于xOy平面对称的点的坐标是 ;关于点A(1,0,2)对称的点的坐标是 .?题型一题型二题型三题型四解析:点P关于x轴对称后,它在x轴的分量不变,在y轴,z轴上的分量变为原来的相反数,所以点P关于x轴的对称点P1的坐标为(-2,-1,-4).
点P关于xOy平面对称后,它在x轴,y轴上的分量均不变,在z轴上的分量变为原来的相反数,
所以点P关于xOy平面的对称点P2的坐标为(-2,1,-4).
设点P关于点A的对称点的坐标为P3(x,y,z),由中点坐标公式可得
故点P关于点A(1,0,2)对称的点P3的坐标为(4,-1,0).
答案:(-2,-1,-4) (-2,1,-4) (4,-1,0)题型一题型二题型三题型四易错点:由于建系不当而致误
【例4】 正三棱柱ABC-A1B1C1各棱长均为1,建立正确的坐标系求点B的坐标时,下列建系方式正确的有( )
(1)以A1为原点,在平面A1B1C1内作A1C1的垂线为x轴,A1C1和AA1所在直线为y轴和z轴建立空间直角坐标系;
(2)以A为原点,分别以AB,AC,A1A所在直线为x轴、y轴、z轴建立空间直角坐标系;
(3)以A1为原点,分别以A1B1,A1C1,A1A所在直线为x轴、y轴、z轴建立空间直角坐标系;
(4)取AC的中点O和A1C1的中点O1,可得BO⊥AC,以O为原点,分别以OB,OC,OO1所在直线为x轴、y轴、z轴建立空间直角坐标系.
A.(2)(3) B.(2)(4) C.(1)(4) D.(3)(4)题型一题型二题型三题型四错解:选A或B或D
错因分析:将(2)(3)误认为x轴和y轴垂直,实际上在正三棱柱ABC-A1B1C1中,∠BAC=∠B1A1C1=60°,所以(2)(3)中的x轴与y轴不垂直,不符合空间直角坐标系的建系要求.
正解:在空间直角坐标系中,三个坐标轴的位置关系是两两互相垂直,(2)(3)中x轴和y轴不垂直,(1)(4)中三个坐标轴两两互相垂直.故选C.
答案:C题型一题型二题型三题型四【变式训练4】 在直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,∠BAC=90°,M是CC1的中点,Q是BC的中点,试建立空间直角坐标系,写出点B,C,C1,M,Q的坐标.
解:因建系不同,所得各点坐标也不同,如以A为原点,分别以AB,AC,AA1所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示,则B(2,0,0),C(0,2,0),C1(0,2,2),M(0,2,1),Q(1,1,0).1 2 3 4 51.设A(2,-3,-1),B(4,7,1),则线段AB的中点在空间直角坐标系中的位置是( )
A.在y轴上 B.在xOy面内
C.在xOz面内 D.在yOz面内
解析:根据中点坐标公式可知,AB的中点坐标为P(3,2,0),故点P在xOy面内.
答案:B1 2 3 4 5答案:D 1 2 3 4 53.已知点A(-3,1,-4),则点A关于原点的对称点A'的坐标为( )
A.(1,-3,-4) B.(-4,1,-3)
C.(3,-1,4) D.(4,-1,3)
答案:C1 2 3 4 54.在空间直角坐标系中,点M(-2,4,-3)在xOz平面上的射影为M',则M'关于原点的对称点是 .?
解析:点M在xOz平面上的射影M'的坐标为(-2,0,-3),M'关于原点的对称点为(2,0,3).
答案:(2,0,3)1 2 3 4 55.在棱长为a的正方体ABCD-A1B1C1D1中,已知B1的坐标为(a,a,a),试写出其余各顶点的坐标.
解:由B1的坐标可知,以顶点D为原点,以棱DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,由正方体的棱长为a可得D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),A1(a,0,a),C1(0,a,a),D1(0,0,a).
