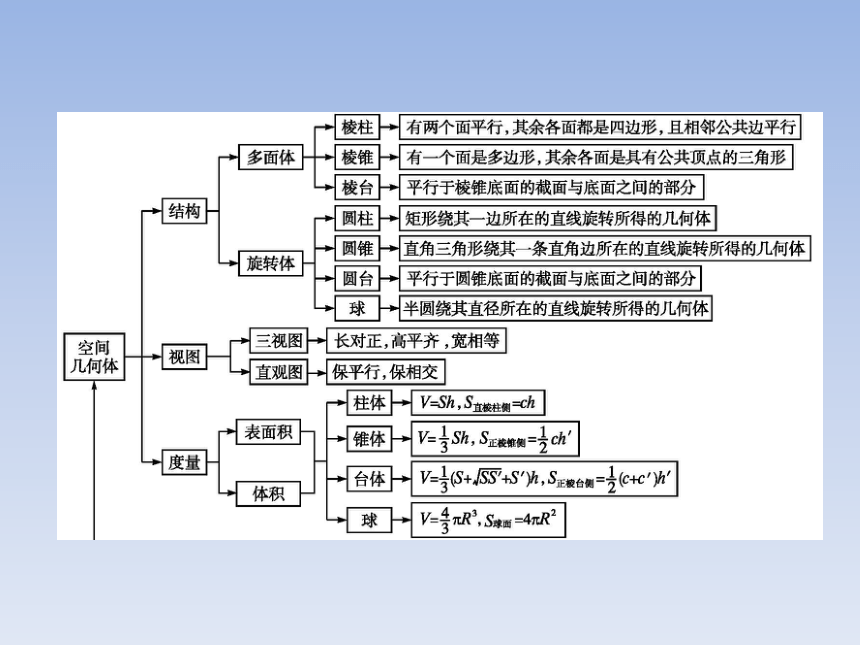
第一章立体几何初步 本章整合:33张PPT
文档属性
| 名称 | 第一章立体几何初步 本章整合:33张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 00:00:00 | ||
图片预览








文档简介
课件33张PPT。本章整合专题1专题2专题3专题4专题5专题1 平行问题
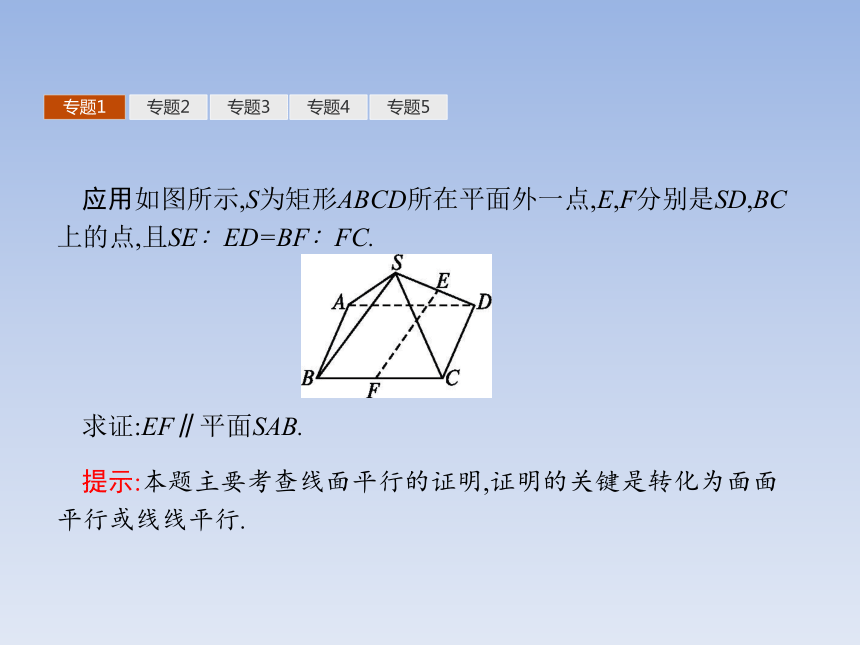
在解决线面平行、面面平行的问题时,利用判定定理,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”,而利用性质定理时,其顺序相反,且“高维”的性质定理就是“低维”的判定方法.特别注意,转化的方法总是由具体题目的条件决定,不能过于呆板僵化,遵循规律而不受制于规律.专题1专题2专题3专题4专题5应用如图所示,S为矩形ABCD所在平面外一点,E,F分别是SD,BC上的点,且SE∶ED=BF∶FC.
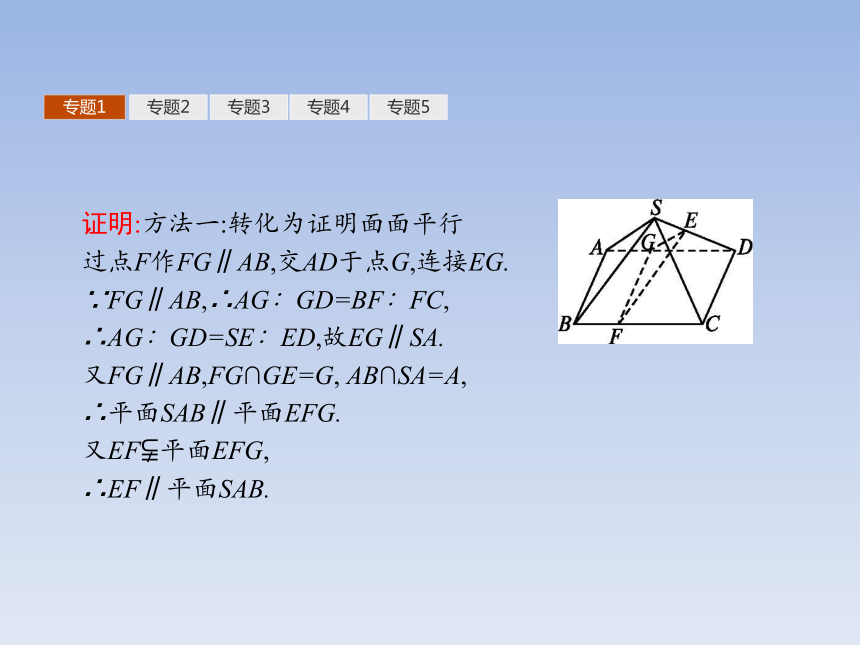
求证:EF∥平面SAB.提示:本题主要考查线面平行的证明,证明的关键是转化为面面平行或线线平行.专题1专题2专题3专题4专题5证明:方法一:转化为证明面面平行
过点F作FG∥AB,交AD于点G,连接EG.
∵FG∥AB,∴AG∶GD=BF∶FC,
∴AG∶GD=SE∶ED,故EG∥SA.
又FG∥AB,FG∩GE=G, AB∩SA=A,
∴平面SAB∥平面EFG.
又EF?平面EFG,
∴EF∥平面SAB.专题1专题2专题3专题4专题5方法二:转化为证明线线平行
过点E作EG∥AD交SA于点G,连接BG.
∵BF∥AD,∴BF∥EG,
∴平面BFEG∩平面SAB=BG.
∵SE∶ED=BF∶FC,∴SE∶SD=BF∶BC.
又SE∶SD=EG∶AD,∴BF∶BC=EG∶AD,
∴BF=EG,故四边形BFEG为平行四边形.
∴EF∥BG,
又EF?平面SAB,BG?平面SAB,
∴EF∥平面SAB.专题1专题2专题3专题4专题5专题2 垂直问题
直线和平面垂直、平面和平面垂直是直线和平面相交、平面和平面相交的特殊情况.对这两种情况的认识,可以从已有的线线垂直、线面垂直关系出发进行推理和论证.无论是线面垂直还是面面垂直,都源于线线垂直,这种“降维”的思想方法很重要.在处理实际问题时,可以从条件入手,分析已有的垂直关系,再从结论“反探”所需的关系,从而架设已知和未知的桥梁.
在垂直的判定定理和性质定理中,有很多限制条件,如“相交直线”“线在面内”“平面经过一直线”等.这些条件一方面有很强的约束性;另一方面又为证明指出了方向.在利用定理时,既要注意定理的严谨性,又要注意推理的规律性.空间中的垂直关系是比平行关系更重要、更灵活多变的一种重要关系.“转化”“降维”是重要的思想方法和解题技巧,应在学习中提炼这些方法.专题1专题2专题3专题4专题5应用关于直线m,n与平面α,β,有下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;
②若m⊥α,n⊥β,且α⊥β,则m⊥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m∥α,n⊥β,且α⊥β,则m∥n.
其中真命题的序号是( )
A.①② B.③④ C.①④ D.②③
答案:D专题1专题2专题3专题4专题5专题3 平面图形的折叠问题
把一个平面图形按某种要求折起,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是折叠问题.
在解决这类问题时,要求既会由平面图形想象出空间图形,又会准确地用空间图形表示出空间物体;既会观察、分析平面图形中各点、线、面在折叠前后的相互关系,又会对图形进行转化.
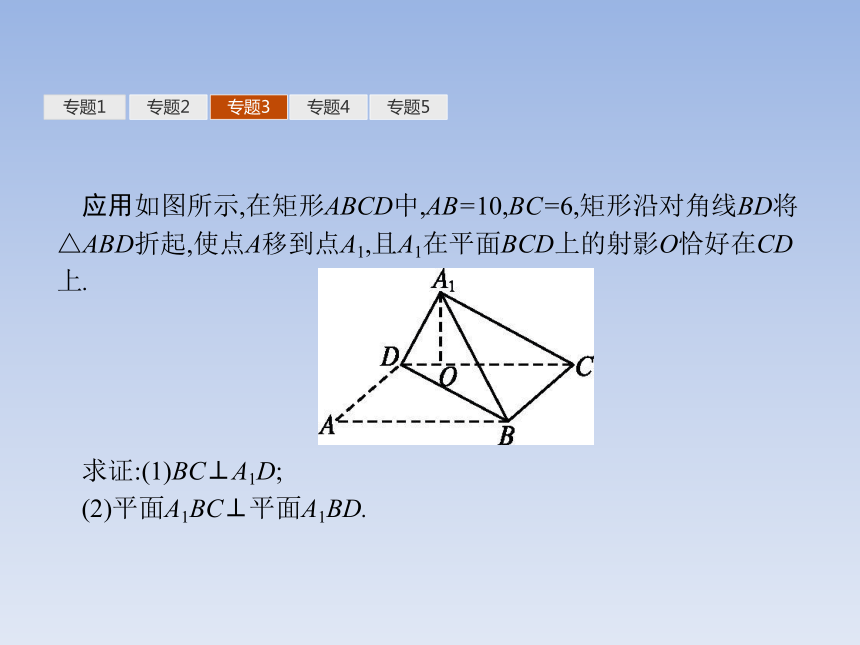
解决折叠问题,要注意折叠前后的变量与不变量,折叠前后同一半平面内的数量关系与位置关系均不发生改变.专题1专题2专题3专题4专题5应用如图所示,在矩形ABCD中,AB=10,BC=6,矩形沿对角线BD将△ABD折起,使点A移到点A1,且A1在平面BCD上的射影O恰好在CD上.
求证:(1)BC⊥A1D;
(2)平面A1BC⊥平面A1BD.专题1专题2专题3专题4专题5证明:(1)∵A1在平面BCD上的射影O在CD上,
∴A1O⊥平面BDC.
又BC?平面BCD,∴BC⊥A1O.
又BC⊥CD,A1O∩CD=O,
∴BC⊥平面A1CD.
又A1D?平面A1CD,
∴BC⊥A1D.
(2)∵四边形ABCD为矩形,
∴A1D⊥A1B.
由(1)知A1D⊥BC,A1B∩BC=B,
∴A1D⊥平面A1BC.
又A1D?平面A1BD,∴平面A1BC⊥平面A1BD.专题1专题2专题3专题4专题5专题4 几何体的表面展开图
常见的几何体中,除了球的表面无法展开在一个平面内,其余几何体的表面展开后,均为一个平面图形,由此产生的表面展开图将空间问题化归为平面问题,转化过程中一般采用“化曲为直”“化折为直”的方法.专题1专题2专题3专题4专题5应用如图所示,在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求:
(1)绳子的最短长度的平方f(x);
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
提示:将圆锥的侧面沿母线SA展开,转化为平面问题.专题1专题2专题3专题4专题5专题1专题2专题3专题4专题5专题1专题2专题3专题4专题5专题5 三视图的应用
三视图是课标高考的新增内容,是高考试题的一个亮点,应予以重视.此类题目的解题关键是利用三视图获取题目中所涉及的基本量的有关信息,这要依靠对三视图的准确理解和把握.专题1专题2专题3专题4专题5应用1在一个几何体的三视图中,主视图和俯视图如图所示,则相应的左视图可以为( )
解析:此几何体为一个半圆锥和一个半三棱锥的组合体,其左视图可以是一个由等腰三角形及其底边上的高构成的平面图形,故选D.
答案:D专题1专题2专题3专题4专题5应用2一个几何体的三视图如图所示,则该几何体的表面积为 .?专题1专题2专题3专题4专题5解析:依题意可知,该几何体是一个半球与一个正四棱柱的组合体,因此该几何体的表面积为22+4×2×3+ ×4π×22+π×22-22=24+12π.
答案:24+12π1 2 3 4 5 6 7 81(2016全国甲高考)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π
B.24π
C.28π
D.32π
解析:因为原几何体由同底面的一个圆柱和一个圆锥构成,
故选C.
答案:C1 2 3 4 5 6 7 82(2016全国乙高考)
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是( )
A.17π B.18π C.20π D.28π
答案:A1 2 3 4 5 6 7 83(2016全国丙高考)
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
C.90
D.81
解析:由题意知该几何体为四棱柱,且四棱柱的底面是边长为3的正方形,侧棱长为3 ,所以所求表面积为(3×3+3×6+3×3 )×2=54+18 ,故选B.
答案:B1 2 3 4 5 6 7 84(2016全国乙高考)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )1 2 3 4 5 6 7 8解析:(方法一)∵α∥平面CB1D1,平面ABCD∥平面A1B1C1D1,α∩平面ABCD=m,平面CB1D1∩平面A1B1C1D1=B1D1,∴m∥B1D1.
∵α∥平面CB1D1,平面ABB1A1∥平面DCC1D1,α∩平面ABB1A1=n,平面CB1D1∩平面DCC1D1=CD1,
∴n∥CD1.
∴B1D1,CD1所成的角等于m,n所成的角,可得∠B1D1C等于m,n所成的角.
∵△B1D1C为正三角形,∴∠B1D1C=60°,
∴m,n所成的角的正弦值为 .1 2 3 4 5 6 7 8(方法二)由题意画出图形如图,将正方体ABCD-A1B1C1D1平移,
补形为两个全等的正方体如图,易证平面AEF∥平面CB1D1,所以平面AEF即为平面α,
m即为AE,n即为AF,所以AE与AF所成的角即为m与n所成的角.
因为△AEF是正三角形,所以∠EAF=60°,
答案:A1 2 3 4 5 6 7 85(2016浙江高考)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
解析:对于选项A,∵α∩β=l,∴l?α,∵m∥α,∴m与l可能平行,也可能异面,故选项A不正确;
对于选项B,D,∵α⊥β,m∥α,n⊥β,∴m与n可能平行,可能相交,也可能异面,故选项B,D不正确.
对于选项C,∵α∩β=l,∴l?β.∵n⊥β,∴n⊥l.故选C.
答案:C1 2 3 4 5 6 7 86(2016山东高考)一个由半球和四棱锥组成的几何体,其三视图如下图所示,则该几何体的体积为( )1 2 3 4 5 6 7 8答案:C 1 2 3 4 5 6 7 87(2016北京高考)某四棱柱的三视图如图所示,则该四棱柱的体积为 .?1 2 3 4 5 6 7 88(2016全国甲高考)如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.
(1)证明:AC⊥HD';1 2 3 4 5 6 7 81 2 3 4 5 6 7 8
在解决线面平行、面面平行的问题时,利用判定定理,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”,而利用性质定理时,其顺序相反,且“高维”的性质定理就是“低维”的判定方法.特别注意,转化的方法总是由具体题目的条件决定,不能过于呆板僵化,遵循规律而不受制于规律.专题1专题2专题3专题4专题5应用如图所示,S为矩形ABCD所在平面外一点,E,F分别是SD,BC上的点,且SE∶ED=BF∶FC.
求证:EF∥平面SAB.提示:本题主要考查线面平行的证明,证明的关键是转化为面面平行或线线平行.专题1专题2专题3专题4专题5证明:方法一:转化为证明面面平行
过点F作FG∥AB,交AD于点G,连接EG.
∵FG∥AB,∴AG∶GD=BF∶FC,
∴AG∶GD=SE∶ED,故EG∥SA.
又FG∥AB,FG∩GE=G, AB∩SA=A,
∴平面SAB∥平面EFG.
又EF?平面EFG,
∴EF∥平面SAB.专题1专题2专题3专题4专题5方法二:转化为证明线线平行
过点E作EG∥AD交SA于点G,连接BG.
∵BF∥AD,∴BF∥EG,
∴平面BFEG∩平面SAB=BG.
∵SE∶ED=BF∶FC,∴SE∶SD=BF∶BC.
又SE∶SD=EG∶AD,∴BF∶BC=EG∶AD,
∴BF=EG,故四边形BFEG为平行四边形.
∴EF∥BG,
又EF?平面SAB,BG?平面SAB,
∴EF∥平面SAB.专题1专题2专题3专题4专题5专题2 垂直问题
直线和平面垂直、平面和平面垂直是直线和平面相交、平面和平面相交的特殊情况.对这两种情况的认识,可以从已有的线线垂直、线面垂直关系出发进行推理和论证.无论是线面垂直还是面面垂直,都源于线线垂直,这种“降维”的思想方法很重要.在处理实际问题时,可以从条件入手,分析已有的垂直关系,再从结论“反探”所需的关系,从而架设已知和未知的桥梁.
在垂直的判定定理和性质定理中,有很多限制条件,如“相交直线”“线在面内”“平面经过一直线”等.这些条件一方面有很强的约束性;另一方面又为证明指出了方向.在利用定理时,既要注意定理的严谨性,又要注意推理的规律性.空间中的垂直关系是比平行关系更重要、更灵活多变的一种重要关系.“转化”“降维”是重要的思想方法和解题技巧,应在学习中提炼这些方法.专题1专题2专题3专题4专题5应用关于直线m,n与平面α,β,有下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;
②若m⊥α,n⊥β,且α⊥β,则m⊥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m∥α,n⊥β,且α⊥β,则m∥n.
其中真命题的序号是( )
A.①② B.③④ C.①④ D.②③
答案:D专题1专题2专题3专题4专题5专题3 平面图形的折叠问题
把一个平面图形按某种要求折起,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是折叠问题.
在解决这类问题时,要求既会由平面图形想象出空间图形,又会准确地用空间图形表示出空间物体;既会观察、分析平面图形中各点、线、面在折叠前后的相互关系,又会对图形进行转化.
解决折叠问题,要注意折叠前后的变量与不变量,折叠前后同一半平面内的数量关系与位置关系均不发生改变.专题1专题2专题3专题4专题5应用如图所示,在矩形ABCD中,AB=10,BC=6,矩形沿对角线BD将△ABD折起,使点A移到点A1,且A1在平面BCD上的射影O恰好在CD上.
求证:(1)BC⊥A1D;
(2)平面A1BC⊥平面A1BD.专题1专题2专题3专题4专题5证明:(1)∵A1在平面BCD上的射影O在CD上,
∴A1O⊥平面BDC.
又BC?平面BCD,∴BC⊥A1O.
又BC⊥CD,A1O∩CD=O,
∴BC⊥平面A1CD.
又A1D?平面A1CD,
∴BC⊥A1D.
(2)∵四边形ABCD为矩形,
∴A1D⊥A1B.
由(1)知A1D⊥BC,A1B∩BC=B,
∴A1D⊥平面A1BC.
又A1D?平面A1BD,∴平面A1BC⊥平面A1BD.专题1专题2专题3专题4专题5专题4 几何体的表面展开图
常见的几何体中,除了球的表面无法展开在一个平面内,其余几何体的表面展开后,均为一个平面图形,由此产生的表面展开图将空间问题化归为平面问题,转化过程中一般采用“化曲为直”“化折为直”的方法.专题1专题2专题3专题4专题5应用如图所示,在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求:
(1)绳子的最短长度的平方f(x);
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
提示:将圆锥的侧面沿母线SA展开,转化为平面问题.专题1专题2专题3专题4专题5专题1专题2专题3专题4专题5专题1专题2专题3专题4专题5专题5 三视图的应用
三视图是课标高考的新增内容,是高考试题的一个亮点,应予以重视.此类题目的解题关键是利用三视图获取题目中所涉及的基本量的有关信息,这要依靠对三视图的准确理解和把握.专题1专题2专题3专题4专题5应用1在一个几何体的三视图中,主视图和俯视图如图所示,则相应的左视图可以为( )
解析:此几何体为一个半圆锥和一个半三棱锥的组合体,其左视图可以是一个由等腰三角形及其底边上的高构成的平面图形,故选D.
答案:D专题1专题2专题3专题4专题5应用2一个几何体的三视图如图所示,则该几何体的表面积为 .?专题1专题2专题3专题4专题5解析:依题意可知,该几何体是一个半球与一个正四棱柱的组合体,因此该几何体的表面积为22+4×2×3+ ×4π×22+π×22-22=24+12π.
答案:24+12π1 2 3 4 5 6 7 81(2016全国甲高考)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π
B.24π
C.28π
D.32π
解析:因为原几何体由同底面的一个圆柱和一个圆锥构成,
故选C.
答案:C1 2 3 4 5 6 7 82(2016全国乙高考)
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是( )
A.17π B.18π C.20π D.28π
答案:A1 2 3 4 5 6 7 83(2016全国丙高考)
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
C.90
D.81
解析:由题意知该几何体为四棱柱,且四棱柱的底面是边长为3的正方形,侧棱长为3 ,所以所求表面积为(3×3+3×6+3×3 )×2=54+18 ,故选B.
答案:B1 2 3 4 5 6 7 84(2016全国乙高考)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )1 2 3 4 5 6 7 8解析:(方法一)∵α∥平面CB1D1,平面ABCD∥平面A1B1C1D1,α∩平面ABCD=m,平面CB1D1∩平面A1B1C1D1=B1D1,∴m∥B1D1.
∵α∥平面CB1D1,平面ABB1A1∥平面DCC1D1,α∩平面ABB1A1=n,平面CB1D1∩平面DCC1D1=CD1,
∴n∥CD1.
∴B1D1,CD1所成的角等于m,n所成的角,可得∠B1D1C等于m,n所成的角.
∵△B1D1C为正三角形,∴∠B1D1C=60°,
∴m,n所成的角的正弦值为 .1 2 3 4 5 6 7 8(方法二)由题意画出图形如图,将正方体ABCD-A1B1C1D1平移,
补形为两个全等的正方体如图,易证平面AEF∥平面CB1D1,所以平面AEF即为平面α,
m即为AE,n即为AF,所以AE与AF所成的角即为m与n所成的角.
因为△AEF是正三角形,所以∠EAF=60°,
答案:A1 2 3 4 5 6 7 85(2016浙江高考)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
解析:对于选项A,∵α∩β=l,∴l?α,∵m∥α,∴m与l可能平行,也可能异面,故选项A不正确;
对于选项B,D,∵α⊥β,m∥α,n⊥β,∴m与n可能平行,可能相交,也可能异面,故选项B,D不正确.
对于选项C,∵α∩β=l,∴l?β.∵n⊥β,∴n⊥l.故选C.
答案:C1 2 3 4 5 6 7 86(2016山东高考)一个由半球和四棱锥组成的几何体,其三视图如下图所示,则该几何体的体积为( )1 2 3 4 5 6 7 8答案:C 1 2 3 4 5 6 7 87(2016北京高考)某四棱柱的三视图如图所示,则该四棱柱的体积为 .?1 2 3 4 5 6 7 88(2016全国甲高考)如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.
(1)证明:AC⊥HD';1 2 3 4 5 6 7 81 2 3 4 5 6 7 8
