黑龙江省哈尔滨市第四十九中学校2019-2020学年第一学期八年级数学9月月考试卷(word版,无答案)
文档属性
| 名称 | 黑龙江省哈尔滨市第四十九中学校2019-2020学年第一学期八年级数学9月月考试卷(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 707.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 14:28:28 | ||
图片预览

文档简介
哈尔滨市第四十九中学校九月学情反馈八年级数学试卷
教师寄语:风雨同载经岁月,华夏儿女共艰辛,坚守信仰谱华章,70华诞笑颜开,勇挑重担于肩上,续写祖国新辉煌。
一、选择题(每题3分,共30分)
我们理应对我们所得的一切心怀感恩,这是我们强大的基础.少年强则国强,中国强则中国少年更强,中国强就是因为少年强.为了庆祝祖国生日小强做了以下几幅剪纸作品,其中是轴对称图形的是( )
A B C D
2.下列运算中,正确的是( )
A. B. C. D.
3.点A(2,-2)关于x轴对称点的坐标为( )
A.(-2,2) B.(-2,-2) C.(2,2) D.(2,-2)
4.等腰三角形的底角为65°,则它的顶角为( )
A.40° B.50° C.60° D.80°
5.等腰三角形的两边长分别是2和7,则它的周长是( )
A.9 B.11 C.16 D.11或16
6.与三角形三个顶点距离相等的点是这个三角形( )
A.三条角分线的交点 B.三条高的交点 C.三条中线的交点 D.两条边的垂直平分线的交点
7.如图,在,BD=2,则AB的长为 ( )
A.4 B.6 C.8 D.10
8.如图,在△ABC中,BC=12,DE为AB的垂直平分线,△BCE的周长为30cm,则AC的长为( )
A.18 B.12 C.10 D.8
9.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 ( )
A.5 B.6 C.7 D.9
10.下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
A.2 B.3 C.4 D.5
二、填空题 (每题3分,共30分)
11.=_________.
12.在△ABC中, AB=AC,∠B=40°,AD⊥BC,则∠CAD=_________.
13.已知点P(a,3)与点Q(-2,b)关于y轴对称,则a+b=_________.
14.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么∠DEF的度数为_______.
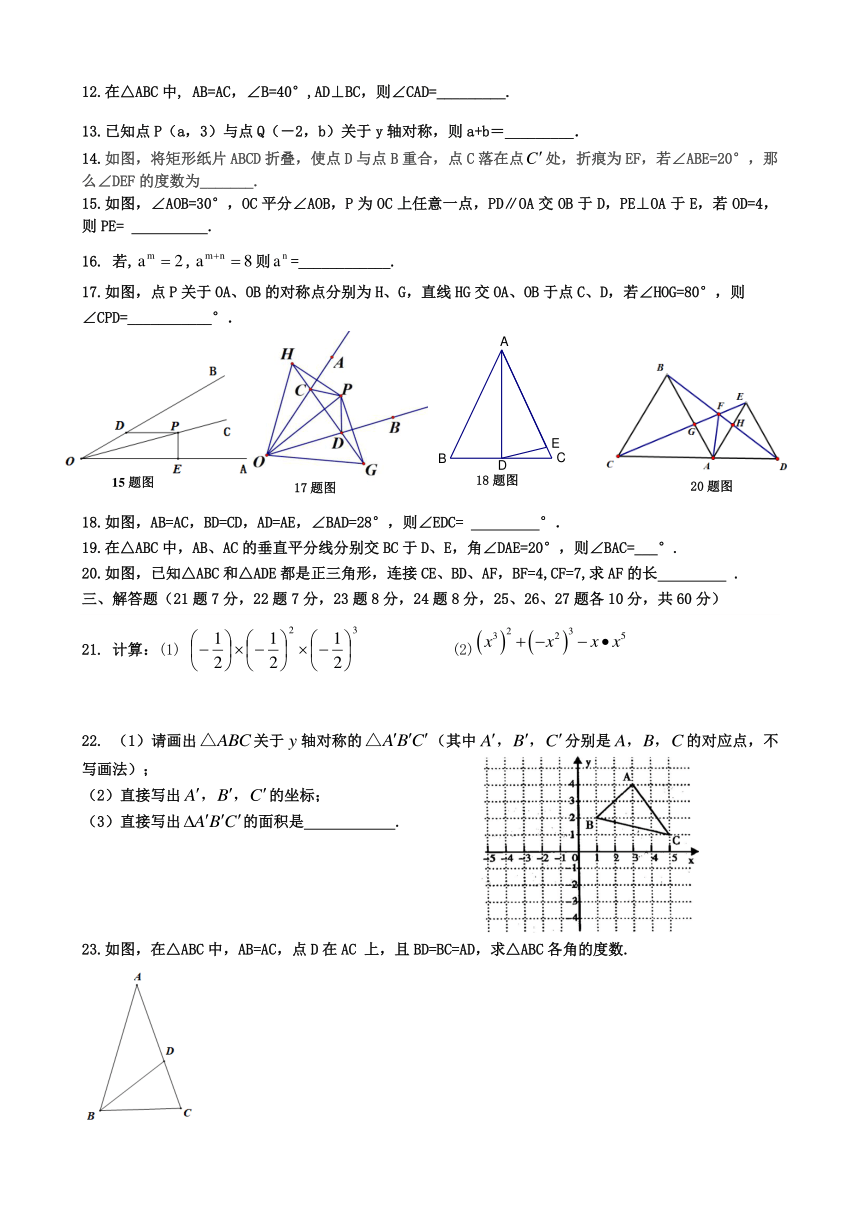
15.如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= .
16. 若,,则=____________.
17.如图,点P关于OA、OB的对称点分别为H、G,直线HG交OA、OB于点C、D,若∠HOG=80°,则
∠CPD=___________°.
18.如图,AB=AC,BD=CD,AD=AE,∠BAD=28°,则∠EDC= °.
19.在△ABC中,AB、AC的垂直平分线分别交BC于D、E,角∠DAE=20°,则∠BAC=___°.
如图,已知△ABC和△ADE都是正三角形,连接CE、BD、AF,BF=4,CF=7,求AF的长 .
三、解答题(21题7分,22题7分,23题8分,24题8分,25、26、27题各10分,共60分)
21. 计算:(1) (2)
22. (1)请画出关于轴对称的(其中分别是的对应点,不写画法);
(2)直接写出的坐标;
(3)直接写出的面积是 .
23.如图,在△ABC中,AB=AC,点D在AC 上,且BD=BC=AD,求△ABC各角的度数.
24.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE
25.为庆祝祖国70周年华诞,阳光超市销售甲、乙两种庆祝商品,该超市若同时购进甲、乙两种商品各10件共花费400元;若购进甲种商品30件,购进乙种商品15件,将用去750元;
(1)求甲、乙两种商品每件的进价;
(2)由于甲、乙两种商品受到市民欢迎,十一月份超市决定购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价为15元,乙种商品每件的售价40元,要使十一月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?
26.在△ABC中,∠B=90°∠A
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
图1 图2
图3
27.如图,A(6, 0),B(0, 4),点B关于x轴的对称点为C点,点D在x轴的负半轴上,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.
(3)在(2)的条件下,同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于y轴的直线上,当△PQR为以PQ为直角边的等腰直角三角形时,求满足条件的t值,并直接写出点R的坐标.
教师寄语:风雨同载经岁月,华夏儿女共艰辛,坚守信仰谱华章,70华诞笑颜开,勇挑重担于肩上,续写祖国新辉煌。
一、选择题(每题3分,共30分)
我们理应对我们所得的一切心怀感恩,这是我们强大的基础.少年强则国强,中国强则中国少年更强,中国强就是因为少年强.为了庆祝祖国生日小强做了以下几幅剪纸作品,其中是轴对称图形的是( )
A B C D
2.下列运算中,正确的是( )
A. B. C. D.
3.点A(2,-2)关于x轴对称点的坐标为( )
A.(-2,2) B.(-2,-2) C.(2,2) D.(2,-2)
4.等腰三角形的底角为65°,则它的顶角为( )
A.40° B.50° C.60° D.80°
5.等腰三角形的两边长分别是2和7,则它的周长是( )
A.9 B.11 C.16 D.11或16
6.与三角形三个顶点距离相等的点是这个三角形( )
A.三条角分线的交点 B.三条高的交点 C.三条中线的交点 D.两条边的垂直平分线的交点
7.如图,在,BD=2,则AB的长为 ( )
A.4 B.6 C.8 D.10
8.如图,在△ABC中,BC=12,DE为AB的垂直平分线,△BCE的周长为30cm,则AC的长为( )
A.18 B.12 C.10 D.8
9.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 ( )
A.5 B.6 C.7 D.9
10.下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
A.2 B.3 C.4 D.5
二、填空题 (每题3分,共30分)
11.=_________.
12.在△ABC中, AB=AC,∠B=40°,AD⊥BC,则∠CAD=_________.
13.已知点P(a,3)与点Q(-2,b)关于y轴对称,则a+b=_________.
14.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么∠DEF的度数为_______.
15.如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= .
16. 若,,则=____________.
17.如图,点P关于OA、OB的对称点分别为H、G,直线HG交OA、OB于点C、D,若∠HOG=80°,则
∠CPD=___________°.
18.如图,AB=AC,BD=CD,AD=AE,∠BAD=28°,则∠EDC= °.
19.在△ABC中,AB、AC的垂直平分线分别交BC于D、E,角∠DAE=20°,则∠BAC=___°.
如图,已知△ABC和△ADE都是正三角形,连接CE、BD、AF,BF=4,CF=7,求AF的长 .
三、解答题(21题7分,22题7分,23题8分,24题8分,25、26、27题各10分,共60分)
21. 计算:(1) (2)
22. (1)请画出关于轴对称的(其中分别是的对应点,不写画法);
(2)直接写出的坐标;
(3)直接写出的面积是 .
23.如图,在△ABC中,AB=AC,点D在AC 上,且BD=BC=AD,求△ABC各角的度数.
24.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE
25.为庆祝祖国70周年华诞,阳光超市销售甲、乙两种庆祝商品,该超市若同时购进甲、乙两种商品各10件共花费400元;若购进甲种商品30件,购进乙种商品15件,将用去750元;
(1)求甲、乙两种商品每件的进价;
(2)由于甲、乙两种商品受到市民欢迎,十一月份超市决定购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价为15元,乙种商品每件的售价40元,要使十一月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?
26.在△ABC中,∠B=90°∠A
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
图1 图2
图3
27.如图,A(6, 0),B(0, 4),点B关于x轴的对称点为C点,点D在x轴的负半轴上,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.
(3)在(2)的条件下,同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于y轴的直线上,当△PQR为以PQ为直角边的等腰直角三角形时,求满足条件的t值,并直接写出点R的坐标.
同课章节目录
