青岛版八年级数学上册第2章 图形的轴对称 2.2 轴对称的基本性质 (2)教案
文档属性
| 名称 | 青岛版八年级数学上册第2章 图形的轴对称 2.2 轴对称的基本性质 (2)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 83.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-15 00:00:00 | ||
图片预览

文档简介
2.2 轴对称的基本性质 (2)
(
学习目标:
)执教者 成武县实验中学 初中 数学 李丽
1 .探索并掌握直角坐标系中关于坐标轴对称的点的坐标规律.
2.利用坐标变换规律,会在平面直角坐标系中画已知图形关于坐标轴成轴对称的图形.
教学过程
一.温故:
1.轴对称的基本性质是什么?
2.已知直线l外一点A,如何画出点A关于l的对称点?
l
A
二 . 知新:
创设情景导入新课: 课件演示 教学楼关于中轴线成轴对称,如果建立坐标系,一个点的坐标记做(a,b),你能写出关于y轴成轴对称的点的坐标吗?
请在坐标纸上画出下列各点关于y轴对称的点,并完成下列表格
完成表格
点 A(4,5) B(6,0) C(-3,-4)
关于y轴对称的点的坐标 A’ B’ C’
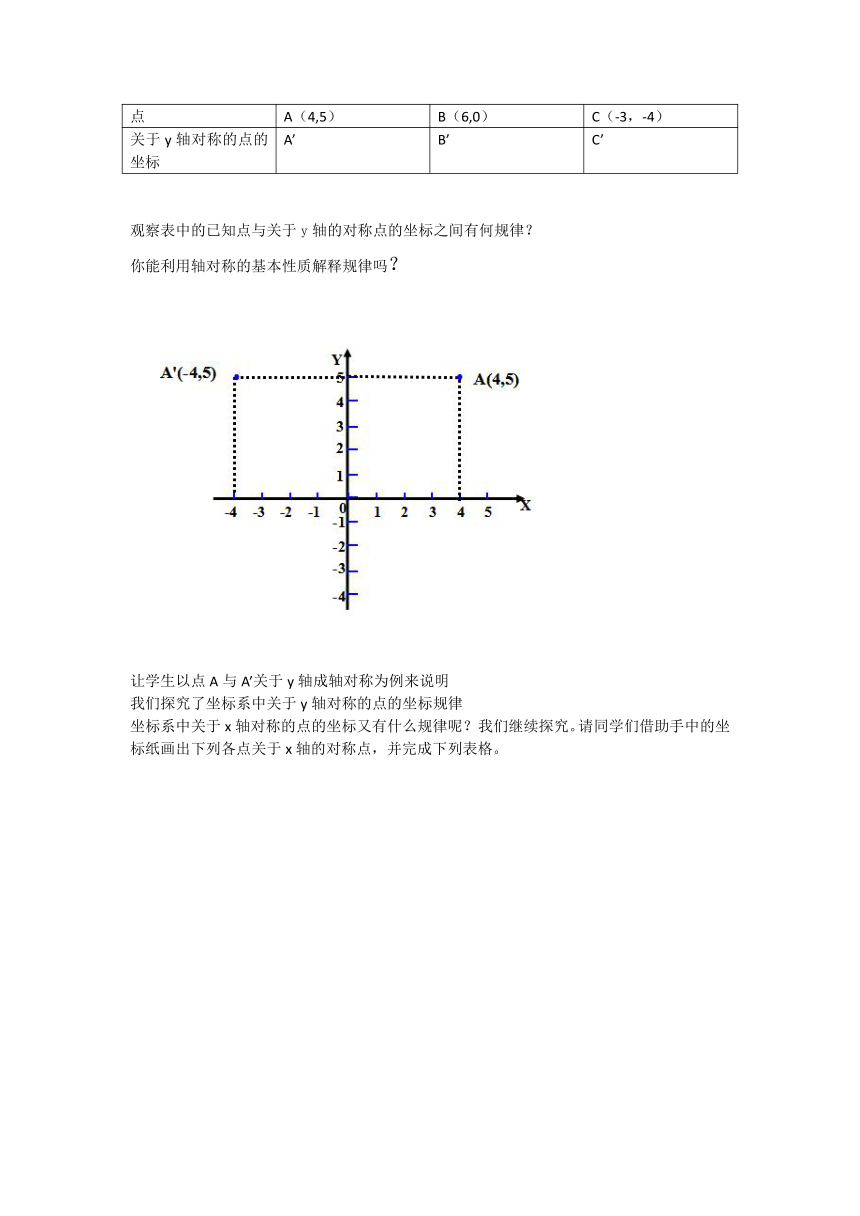
观察表中的已知点与关于y轴的对称点的坐标之间有何规律?
你能利用轴对称的基本性质解释规律吗?
让学生以点A与A’关于y轴成轴对称为例来说明
我们探究了坐标系中关于y轴对称的点的坐标规律
坐标系中关于x轴对称的点的坐标又有什么规律呢?我们继续探究。请同学们借助手中的坐标纸画出下列各点关于x轴的对称点,并完成下列表格。
完成表格
点 A(4,5) B(0,3) C(-3,-4) D(3,0)
关于x轴对称的点的坐标 A’ B’ C’ D’
关于x轴对称的点的坐标有何规律?
P(a,b)关于x轴对称的点的坐标(a,-b)
P(a,b)关于y轴对称的点的坐标(-a,b)
这就是坐标系中关于坐标轴对称的点的坐标规律。
识记1分钟,再提问
你怎样快速记住这个规律呢?
简记成一句口诀:关于谁对称谁不变。
请利用规律抢答下题
小试牛刀
1.抢答
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴对称的点的坐标
关于y轴对称的点的坐标
2.点M(a,-5)与点N(-2,b) 若关于y轴对称,则a=_______,b=__________
若关于x轴对称,则a=_________,b=____________
你能解决开头提出的问题了吗?
通过上节课的学习,我们会画一个图形关于一条直线成轴对称的图形,怎么画?
如果把这个三角形放在坐标系中,你能画出这个三角形关于y轴成轴对称的图形吗?
例2
如图,在直角坐标系中,已知?ABC的顶点坐标分别是A(-2,1),B(1.5,-4)和C(0,3)请画出?ABC关于y轴对称的?A’B’C’
学生思考,说解题思路,
教师板书规范的解题步骤
通过例2你能总结解题步骤吗?
写出关键点的对称点的坐标;
描点
连线
学以致用:
如图,在直角坐标系中,已知?ABC的顶点坐标分别是A(-2,1),B(1.5,-4)和C(0,3)请画出?ABC关于x轴对称的?A’’B’’C’’
小结:本节课你有哪些收获?
检测:
点P(-4,7)与点Q关于x轴对称,则点Q的坐标为_____________,点P与点Q关于y轴对称,则点Q的坐标为_______________.
已知点A(m+2,3)点B(-5,n+6)关于y轴对称,则m=__________, n=__________.
若一个点的纵坐标不变,将横坐标乘以-1,得到的点与原来的点的位置关系是___________.
若一个点的横坐标不变,将纵坐标乘以-1,得到的点与原来的点的位置关系是___________.
4.点A(-3,2)与点B(-3,-2)的关系是 ( )
A. 关于x轴对称 A. 关于y轴对称
C. 关于原点对称 D . 以上各项都不对
5. 已知点P(a-1,5)和点Q(2,b-1)关于x轴对称,则a=____________, b=______________.
作业: 习题 2.2 必做 4题 5题
选做 7题
板书设计:
2.2 轴对称的基本性质 (2)
一.关于坐标轴对称的点的坐标的变换规律
点p(a,b)关于y轴对称的点P’(-a,b),
关于x轴对称的点P’’(a,-b)
画一个图形关于对称轴成轴对称的图形
步骤 1.写关键点的对称点的坐标;
2描点
3 顺次连接各点画出图形
(
学习目标:
)执教者 成武县实验中学 初中 数学 李丽
1 .探索并掌握直角坐标系中关于坐标轴对称的点的坐标规律.
2.利用坐标变换规律,会在平面直角坐标系中画已知图形关于坐标轴成轴对称的图形.
教学过程
一.温故:
1.轴对称的基本性质是什么?
2.已知直线l外一点A,如何画出点A关于l的对称点?
l
A
二 . 知新:
创设情景导入新课: 课件演示 教学楼关于中轴线成轴对称,如果建立坐标系,一个点的坐标记做(a,b),你能写出关于y轴成轴对称的点的坐标吗?
请在坐标纸上画出下列各点关于y轴对称的点,并完成下列表格
完成表格
点 A(4,5) B(6,0) C(-3,-4)
关于y轴对称的点的坐标 A’ B’ C’
观察表中的已知点与关于y轴的对称点的坐标之间有何规律?
你能利用轴对称的基本性质解释规律吗?
让学生以点A与A’关于y轴成轴对称为例来说明
我们探究了坐标系中关于y轴对称的点的坐标规律
坐标系中关于x轴对称的点的坐标又有什么规律呢?我们继续探究。请同学们借助手中的坐标纸画出下列各点关于x轴的对称点,并完成下列表格。
完成表格
点 A(4,5) B(0,3) C(-3,-4) D(3,0)
关于x轴对称的点的坐标 A’ B’ C’ D’
关于x轴对称的点的坐标有何规律?
P(a,b)关于x轴对称的点的坐标(a,-b)
P(a,b)关于y轴对称的点的坐标(-a,b)
这就是坐标系中关于坐标轴对称的点的坐标规律。
识记1分钟,再提问
你怎样快速记住这个规律呢?
简记成一句口诀:关于谁对称谁不变。
请利用规律抢答下题
小试牛刀
1.抢答
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴对称的点的坐标
关于y轴对称的点的坐标
2.点M(a,-5)与点N(-2,b) 若关于y轴对称,则a=_______,b=__________
若关于x轴对称,则a=_________,b=____________
你能解决开头提出的问题了吗?
通过上节课的学习,我们会画一个图形关于一条直线成轴对称的图形,怎么画?
如果把这个三角形放在坐标系中,你能画出这个三角形关于y轴成轴对称的图形吗?
例2
如图,在直角坐标系中,已知?ABC的顶点坐标分别是A(-2,1),B(1.5,-4)和C(0,3)请画出?ABC关于y轴对称的?A’B’C’
学生思考,说解题思路,
教师板书规范的解题步骤
通过例2你能总结解题步骤吗?
写出关键点的对称点的坐标;
描点
连线
学以致用:
如图,在直角坐标系中,已知?ABC的顶点坐标分别是A(-2,1),B(1.5,-4)和C(0,3)请画出?ABC关于x轴对称的?A’’B’’C’’
小结:本节课你有哪些收获?
检测:
点P(-4,7)与点Q关于x轴对称,则点Q的坐标为_____________,点P与点Q关于y轴对称,则点Q的坐标为_______________.
已知点A(m+2,3)点B(-5,n+6)关于y轴对称,则m=__________, n=__________.
若一个点的纵坐标不变,将横坐标乘以-1,得到的点与原来的点的位置关系是___________.
若一个点的横坐标不变,将纵坐标乘以-1,得到的点与原来的点的位置关系是___________.
4.点A(-3,2)与点B(-3,-2)的关系是 ( )
A. 关于x轴对称 A. 关于y轴对称
C. 关于原点对称 D . 以上各项都不对
5. 已知点P(a-1,5)和点Q(2,b-1)关于x轴对称,则a=____________, b=______________.
作业: 习题 2.2 必做 4题 5题
选做 7题
板书设计:
2.2 轴对称的基本性质 (2)
一.关于坐标轴对称的点的坐标的变换规律
点p(a,b)关于y轴对称的点P’(-a,b),
关于x轴对称的点P’’(a,-b)
画一个图形关于对称轴成轴对称的图形
步骤 1.写关键点的对称点的坐标;
2描点
3 顺次连接各点画出图形
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
