北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第1讲 等腰三角形(提高,附答案)
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第1讲 等腰三角形(提高,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 214.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 23:11:53 | ||
图片预览



文档简介
等腰三角形(提高)知识讲解
【学习目标】
1. 了解等腰三角形、等边三角形的有关概念, 掌握等腰三角形的轴对称性;
2. 掌握等腰三角形、等边三角形的性质,会利用这些性质进行简单的推理、证明、计算和作图.
3. 理解并掌握等腰三角形、等边三角形的判定方法及其证明过程. 通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
4. 理解反证法并能用反证法推理证明简单几何题.
【要点梳理】
要点一、等腰三角形的定义
1.等腰三角形
有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,△ABC是等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
/
2.等腰三角形的作法
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
/
作法:1.作线段BC=a;
2.分别以B,C为圆心,以b为半径画弧,两弧
相交于点A;
3.连接AB,AC.
△ABC为所求作的等腰三角形
3.等腰三角形的对称性
(1)等腰三角形是轴对称图形;
(2)∠B=∠C;
(3)BD=CD,AD为底边上的中线.
/
(4)∠ADB=∠ADC=90°,AD为底边上的高线.
结论:等腰三角形是轴对称图形,顶角平分线(底边上的高线或中线)所在的直线是它的对称轴.
4.等边三角形
三条边都相等的三角形叫做等边三角形.也称为正三角形.等边三角形是一类特殊的等腰三角形,有三条对称轴,每个角的平分线(底边上的高线或中线)所在的直线就是它的对称轴.
要点诠释:(1)等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A=180°-2∠B,∠B=∠C=/ .
(2)等边三角形与等腰三角形的关系:等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
要点二、等腰三角形的性质
1.等腰三角形的性质
性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
推论:等边三角形的三个内角都相等,并且每个内角都等于60°.
性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
2.等腰三角形中重要线段的性质
等腰三角形的两底角的平分线(两腰上的高、两腰上的中线)相等.
要点诠释:这条性质,还可以推广到以下结论:
(1)等腰三角形底边上的高上任一点到两腰的距离相等。
(2)等腰三角形两底边上的中点到两腰的距离相等.
(3)等腰三角形两底角平分线,两腰上的中线,两腰上的高的交点到两腰的距离相等,到底边两端上的距离相等.
(4)等腰三角形顶点到两腰上的高、中线、角平分线的距离相等.
要点三、等腰三角形的判定定理
1.等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
要点诠释:(1)要弄清判定定理的条件和结论,不要与性质定理混淆.判定定理得到的结论是等腰三角形,性质定理是已知三角形是等腰三角形,得到边和角关系.
(2)不能说“一个三角形两底角相等,那么两腰边相等”,因为还未判定它是一个等腰三角形.
2.等边三角形的判定定理
三个角相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
3. 含有30°角的直角三角形
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点四、反证法
在证明时,先假设命题的结论不成立,然后从这个假设出发,经过逐步推导论证,最后推出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果,从而证明命题的结论一定成立,这种证明命题的方法叫做反证法.
要点诠释:反证法也称归谬法,是一种间接证明的方法,一般适用于直接证明有困难的命题.一般证明步骤如下:
(1) 假定命题的结论不成立; (2) 从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果; (3)由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
类型一、等腰三角形中的分类讨论
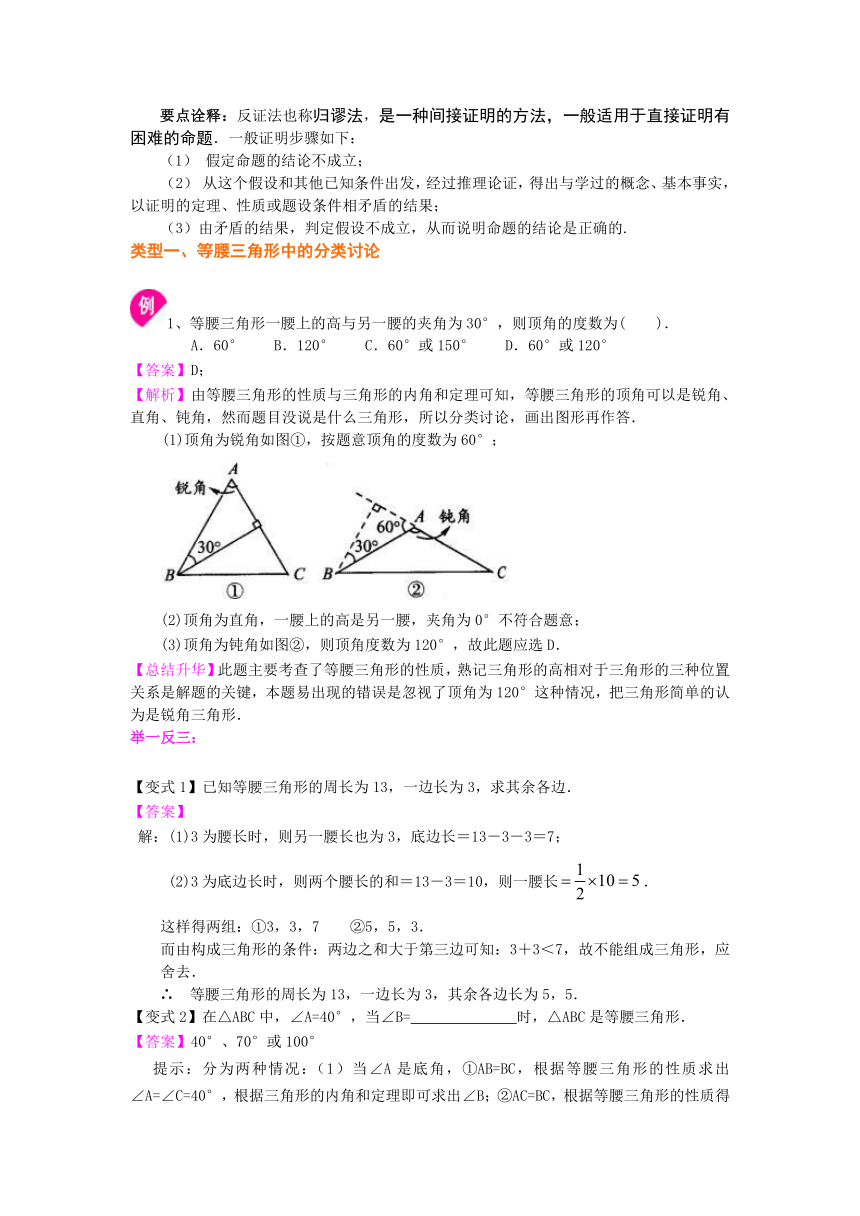
/1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ).
A.60° B.120° C.60°或150° D.60°或120°
【答案】D;
【解析】由等腰三角形的性质与三角形的内角和定理可知,等腰三角形的顶角可以是锐角、直角、钝角,然而题目没说是什么三角形,所以分类讨论,画出图形再作答.
(1)顶角为锐角如图①,按题意顶角的度数为60°;
/
(2)顶角为直角,一腰上的高是另一腰,夹角为0°不符合题意;
(3)顶角为钝角如图②,则顶角度数为120°,故此题应选D.
【总结升华】此题主要考查了等腰三角形的性质,熟记三角形的高相对于三角形的三种位置关系是解题的关键,本题易出现的错误是忽视了顶角为120°这种情况,把三角形简单的认为是锐角三角形.
举一反三:
【变式1】已知等腰三角形的周长为13,一边长为3,求其余各边.
【答案】
解:(1)3为腰长时,则另一腰长也为3,底边长=13-3-3=7;
(2)3为底边长时,则两个腰长的和=13-3=10,则一腰长/.
这样得两组:①3,3,7 ②5,5,3.
而由构成三角形的条件:两边之和大于第三边可知:3+3<7,故不能组成三角形,应舍去.
∴ 等腰三角形的周长为13,一边长为3,其余各边长为5,5.
【变式2】在△ABC中,∠A=40°,当∠B= 时,△ABC是等腰三角形.
【答案】40°、70°或100°
提示:分为两种情况:(1)当∠A是底角,①AB=BC,根据等腰三角形的性质求出∠A=∠C=40°,根据三角形的内角和定理即可求出∠B;②AC=BC,根据等腰三角形的性质得到∠A=∠B=40°;(2)当∠A是顶角时,AB=AC,根据等腰三角形的性质和三角形的内角和定理即可求出∠B.
类型二、等腰三角形的操作题
/2、如图,请将下列两个三角形分成两个等腰三角形.(要求标出每个等腰三角形的内角度数)
/
【思路点拨】根据等腰三角形的判定定理在左图△ABC中的边BC上取一点D,使BD=AD即可;在右图△ABC中的边AC上取一点D,使BD=CD即可.
【答案与解析】
解:如图(1)所示:在BC上取一点D,使∠ADB=110°,∠ADC=70°,∠BAD=35°,∠CAD=40°,
/
如图(2)所示:在AC上取一点D,使∠ABD=32°,∠CBD=16°,∠ADB=32°,
/
∠BDC=148°.
【总结升华】本题考查了等腰三角形的性质和判定、三角形的内角和定理等知识点,关键是根据题意画出图形,注意应先确定等腰三角形的各个角的度数,再根据度数画出图形.
举一反三:
【变式】(2019?温州模拟)如图,有甲,乙两个三角形,请你用一条直线把每一个三角形分成两个等腰三角形,并标出每个三角形各角的度数.
/ /
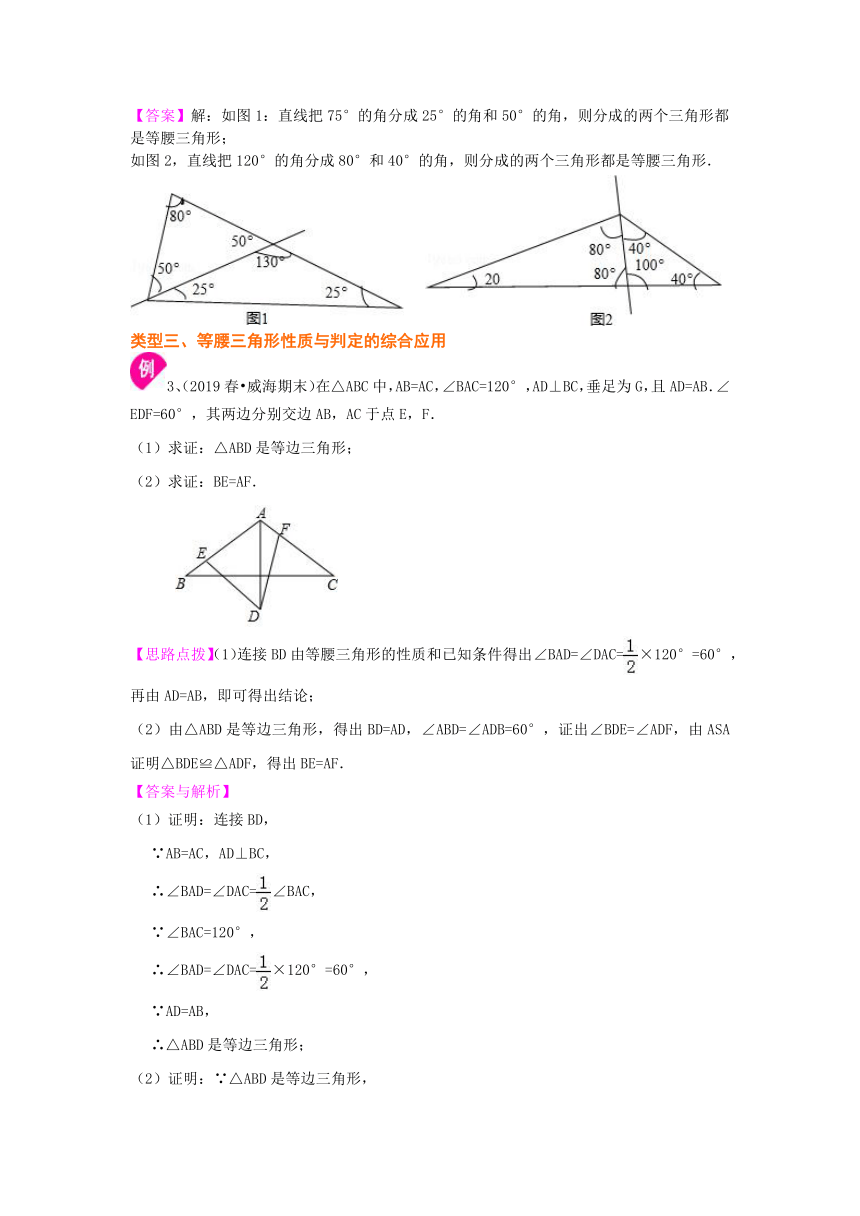
【答案】解:如图1:直线把75°的角分成25°的角和50°的角,则分成的两个三角形都是等腰三角形;
如图2,直线把120°的角分成80°和40°的角,则分成的两个三角形都是等腰三角形.
/ /
类型三、等腰三角形性质与判定的综合应用
/3、(2019春?威海期末)在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.
/
【思路点拨】(1)连接BD由等腰三角形的性质和已知条件得出∠BAD=∠DAC=/×120°=60°,再由AD=AB,即可得出结论;
(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.
【答案与解析】
(1)证明:连接BD,
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=/∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=/×120°=60°,
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
/,
∴△BDE≌△ADF(ASA),
∴BE=AF.
/
【总结升华】本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
举一反三:
【变式】如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有 个.
/
【答案】4;
提示:根据等腰三角形的判定,由已知可证∠BAD=∠CAD=∠B=30°,即证△ADB是等腰三角形;又证CD=DE,AE=AC,即证△CDE,△AEC是等腰三角形;再证ECB=∠B=30°,即证△BEC是等腰三角形.即图中的等腰三角形共有4个.
/4、如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F,求证:CE=CF.
/
【思路点拨】根据三角形的内角和定理得出∠CAF+∠CFA=90°,∠FAD+∠AED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,根据等腰三角形的判定推出即可.
【答案与解析】
证明:∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF.
【总结升华】本题考查了直角三角形性质,等腰三角形的性质和判定,三角形的内角和定理,关键是推出∠CEF=∠CFE.
举一反三:
【变式】如图是由9个等边三角形拼成的六边形,现已知中间最小的等边三角形的边长是a,则围成的六边形的周长为( )
/
A. 30a B. 32a C. 34a D. 无法计算
【答案】A;
提示:设右下角第二个小的等边三角形的边长是x,则剩下的7个等边三角形的边长是x; x; x+a; x+a; x+2a ;x+2a; x+3a,根据题意得到方程2x=x+3a,求出x=3a,即可求出围成的六边形的周长.
类型四、含30°角的直角三角形
/5、如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然
后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
/
【思路点拨】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD,再根据等角对等边的性质可得AD=CD,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
【答案与解析】
解:∵∠ACB=15°,∠ADB=30°, ∴∠CAD=∠ADB-∠ACB=30°-15°=15°, 即△CAD为等腰三角形, ∴AD=CD=13, 在△ADB中,∵AB⊥DB,∠ADB=30°, ∴AB=/AD=/×13=6.5(m).
【总结升华】本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,熟记性质是解题的关键.
举一反三:
【变式】已知:如图,在Rt△ABC中,∠C=90°,∠BAD=/∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=/DB.
/
【答案】
解:∵DE⊥AB, ∴∠AED=∠BED=90°, ∵DE是∠ADB的平分线, ∴∠3=∠4,又∵DE=DE, ∴△BED≌△AED(ASA), ∴AD=BD,∠2=∠B, ∵∠BAD=∠2=/∠BAC, ∴∠1=∠2=∠B, ∴AD=BD, 又∵∠1+∠2+∠B=90°, ∴∠B=∠1=∠2=30°, 在直角三角形ACD中,∠1=30°, ∴CD= /AD= /BD.
类型五、反证法
/6、求证:在一个三角形中,如果两个角不等,那么它们所对的边也不等.
【思路点拨】先假设它们的对边相等,然后根据等腰三角形的性质得出假设不成立,从而证得原结论成立.
【答案与解析】
证明:假设它们所对的边相等;
则根据等腰三角形的性质定理,“等边对等角”所以等它们所对的角也相等;
这就与题设两个角不等相矛盾;
因此假设不成立,故原结论成立.
【总结升华】本题结合等腰三角形的性质考查反证法,解此题关键要懂得反证法的意义及步骤.
举一反三:
【变式】用反证法证明“三角形三个内角中至少有两个锐角”时应首先假设
.
【答案】三角形三个内角中最多有一个锐角.
【巩固练习】
一.选择题
1.如图,在△ABC中,若AB=AC,BC=BD,AD=DE=EB,则∠A等于( ).
A.30° B.36° C.45° D.54°
/
2.用反证法证明:a,b至少有一个为0,应假设( )
A. a,b没有一个为0
B. a,b只有一个为0
C. a,b至多有一个为0
D. a,b两个都为0
3. 如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的有( )
①△BDF,△CEF都是等腰三角形; ②DE=DB+CE;
③AD+DE+AE=AB+AC; ④BF=CF. A.1个 B.2个 C.3个 D.4个
/
4. 等腰三角形一腰上的高与底边所成的角等于( )
A.顶角的一半 B.底角的一半 C.90°减去顶角的一半 D.90°减去底角的一半
5.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )
/
A./cm B.2cm C.3cm D.4cm
6. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
/
二.填空题
7.(2019?通辽)等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为 .
8. 用反证法证明“若|a|≠|b|,则a≠b.”时,应假设 .
9. 等腰三角形的周长为22/,其中一边的长是8/,则其余两边长分别为________.
10.(2019春?盐城校级月考)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,当t= 时,△ABD为等腰三角形.
/
11.如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF =_________°.
/
12. 如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
/ 三.解答题
13. 用反证法证明:一条线段只有一个中点.
14.(2019秋?宜昌期中)一个等腰三角形的三边长分别为x,2x﹣3,4x﹣6,求这个三角形的周长.
15.(2019秋?东台市期中)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
/
【答案与解析】
一.选择题
1. 【答案】C;
【解析】设∠A=/,则由题意∠ADE=180°-2/,∠EDB=/,∠BDC=∠BCD=90°-/,因为∠ADE+∠EDB+∠BDC=180°,所以/=45°.
2. 【答案】A;
【解析】由于命题:“a,b至少有一个为0”的反面是:“a,b没有一个为0”,故选A.
3. 【答案】C ;
【解析】①②③正确.
4. 【答案】A;
【解析】解:△ABC中,∵AB=AC,BD是高, ∴∠ABC=∠C=/ 在Rt△BDC中,∠CBD=90°-∠C=90°-/=/. 故选A.
/
5. 【答案】C;
【解析】解:∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm,
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm;
故选:C.
6. 【答案】D;
【解析】解:根据垂线段最短,可知AP的长不可小于3; ∵△ABC中,∠C=90°,AC=3,∠B=30°, ∴AB=6, ∴AP的长不能大于6. 故选D.
二.填空题
7. 【答案】69°或21°;
【解析】解:分两种情况讨论:
①若∠A<90°,如图1所示:
/
∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=48°,
∴∠A=90°﹣48°=42°,
∵AB=AC,
∴∠ABC=∠C=/(180°﹣42°)=69°;
②若∠A>90°,如图2所示:
/
同①可得:∠DAB=90°﹣48°=42°,
∴∠BAC=180°﹣42°=138°,
∵AB=AC,
∴∠ABC=∠C=/(180°﹣138°)=21°;
综上所述:等腰三角形底角的度数为69°或21°.
故答案为:69°或21°.
8. 【答案】a=b;
【解析】a,b的等价关系有a=b,a≠b两种情况,因而a≠b的反面是a=b.
9. 【答案】7/,7/或8/,6/;
【解析】边长为8cm的可能是底边,也可能是腰.
10.【答案】5,6,/;
【解析】解:在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm,由勾股定理得:AC=3cm,
由运动可知:AD=t,且△ABD时等腰三角形,
有三种情况:
①若AB=AD,则t=5;
②若BA=BD,则AD=2AC,即t=6;
③若DA=DB,则在Rt△BCD中,CD=t﹣3,BC=4,BD=t,
即(t﹣3)2+42=t2,
解得:t=/,
综合上述:符合要求的t值有3个,分别为5,6,/.
11.【答案】40;
【解析】AD=FD,∠FAD=∠AFD=70°,所以∠ADF=40°.
12.【答案】15°;
【解析】设∠A=/,∠BED=∠EBD=2/,∠CBD=120°-2/,∠C=∠BDC=30°+/,
而∠A+∠C=60°,所以/+30°+/ =60°,解得/=15°.
三.解答题
13.【解析】
已知:一条线段AB,M为AB的中点.
求证:线段AB只有一个中点M.
证明:假设线段AB有两个中点M、N,不妨设M在N的左边,
则AM<AN,
又因为AM=/AB=AN=/AB,
这与AM<AN矛盾,
所以线段AB只有一个中点M.
14.【解析】
解:①x=2x﹣3,则x=3,
∴4x﹣6=6,
∵3+3=6,
∴3、3、6不能构成三角形;
②x=4x﹣6,则x=2,
∴2x﹣3=1,
∵1、2、2任意两边之和大于第三边,
∴这个三角形的周长为1+2+2=5;
③2x﹣3=4x﹣6,则x=/,
∴2x﹣3=0,
∴此三角形不存在.
综上可知:这个三角形的周长为5.
15.【解析】
解:(1)∵∠C=90°,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴有勾股定理得PB=2/cm
∴△ABP的周长为:AP+PB+AB=6+10+2/=(16+2/)cm;
(2)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形;
(3)当P点在AC上,Q在AB上,则AP=8﹣t,AQ=16﹣2t,
∵直线PQ把△ABC的周长分成相等的两部分,
∴8﹣t+16﹣2t=12,
∴t=4;
当P点在AB上,Q在AC上,则AP=t﹣8,AQ=2t﹣16,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t﹣8+2t﹣16=12,
∴t=12,
∴当t为4或12秒时,直线PQ把△ABC的周长分成相等的两部分.
【学习目标】
1. 了解等腰三角形、等边三角形的有关概念, 掌握等腰三角形的轴对称性;
2. 掌握等腰三角形、等边三角形的性质,会利用这些性质进行简单的推理、证明、计算和作图.
3. 理解并掌握等腰三角形、等边三角形的判定方法及其证明过程. 通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
4. 理解反证法并能用反证法推理证明简单几何题.
【要点梳理】
要点一、等腰三角形的定义
1.等腰三角形
有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,△ABC是等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
/
2.等腰三角形的作法
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
/
作法:1.作线段BC=a;
2.分别以B,C为圆心,以b为半径画弧,两弧
相交于点A;
3.连接AB,AC.
△ABC为所求作的等腰三角形
3.等腰三角形的对称性
(1)等腰三角形是轴对称图形;
(2)∠B=∠C;
(3)BD=CD,AD为底边上的中线.
/
(4)∠ADB=∠ADC=90°,AD为底边上的高线.
结论:等腰三角形是轴对称图形,顶角平分线(底边上的高线或中线)所在的直线是它的对称轴.
4.等边三角形
三条边都相等的三角形叫做等边三角形.也称为正三角形.等边三角形是一类特殊的等腰三角形,有三条对称轴,每个角的平分线(底边上的高线或中线)所在的直线就是它的对称轴.
要点诠释:(1)等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A=180°-2∠B,∠B=∠C=/ .
(2)等边三角形与等腰三角形的关系:等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
要点二、等腰三角形的性质
1.等腰三角形的性质
性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
推论:等边三角形的三个内角都相等,并且每个内角都等于60°.
性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
2.等腰三角形中重要线段的性质
等腰三角形的两底角的平分线(两腰上的高、两腰上的中线)相等.
要点诠释:这条性质,还可以推广到以下结论:
(1)等腰三角形底边上的高上任一点到两腰的距离相等。
(2)等腰三角形两底边上的中点到两腰的距离相等.
(3)等腰三角形两底角平分线,两腰上的中线,两腰上的高的交点到两腰的距离相等,到底边两端上的距离相等.
(4)等腰三角形顶点到两腰上的高、中线、角平分线的距离相等.
要点三、等腰三角形的判定定理
1.等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
要点诠释:(1)要弄清判定定理的条件和结论,不要与性质定理混淆.判定定理得到的结论是等腰三角形,性质定理是已知三角形是等腰三角形,得到边和角关系.
(2)不能说“一个三角形两底角相等,那么两腰边相等”,因为还未判定它是一个等腰三角形.
2.等边三角形的判定定理
三个角相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
3. 含有30°角的直角三角形
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点四、反证法
在证明时,先假设命题的结论不成立,然后从这个假设出发,经过逐步推导论证,最后推出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果,从而证明命题的结论一定成立,这种证明命题的方法叫做反证法.
要点诠释:反证法也称归谬法,是一种间接证明的方法,一般适用于直接证明有困难的命题.一般证明步骤如下:
(1) 假定命题的结论不成立; (2) 从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,以证明的定理、性质或题设条件相矛盾的结果; (3)由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
类型一、等腰三角形中的分类讨论
/1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ).
A.60° B.120° C.60°或150° D.60°或120°
【答案】D;
【解析】由等腰三角形的性质与三角形的内角和定理可知,等腰三角形的顶角可以是锐角、直角、钝角,然而题目没说是什么三角形,所以分类讨论,画出图形再作答.
(1)顶角为锐角如图①,按题意顶角的度数为60°;
/
(2)顶角为直角,一腰上的高是另一腰,夹角为0°不符合题意;
(3)顶角为钝角如图②,则顶角度数为120°,故此题应选D.
【总结升华】此题主要考查了等腰三角形的性质,熟记三角形的高相对于三角形的三种位置关系是解题的关键,本题易出现的错误是忽视了顶角为120°这种情况,把三角形简单的认为是锐角三角形.
举一反三:
【变式1】已知等腰三角形的周长为13,一边长为3,求其余各边.
【答案】
解:(1)3为腰长时,则另一腰长也为3,底边长=13-3-3=7;
(2)3为底边长时,则两个腰长的和=13-3=10,则一腰长/.
这样得两组:①3,3,7 ②5,5,3.
而由构成三角形的条件:两边之和大于第三边可知:3+3<7,故不能组成三角形,应舍去.
∴ 等腰三角形的周长为13,一边长为3,其余各边长为5,5.
【变式2】在△ABC中,∠A=40°,当∠B= 时,△ABC是等腰三角形.
【答案】40°、70°或100°
提示:分为两种情况:(1)当∠A是底角,①AB=BC,根据等腰三角形的性质求出∠A=∠C=40°,根据三角形的内角和定理即可求出∠B;②AC=BC,根据等腰三角形的性质得到∠A=∠B=40°;(2)当∠A是顶角时,AB=AC,根据等腰三角形的性质和三角形的内角和定理即可求出∠B.
类型二、等腰三角形的操作题
/2、如图,请将下列两个三角形分成两个等腰三角形.(要求标出每个等腰三角形的内角度数)
/
【思路点拨】根据等腰三角形的判定定理在左图△ABC中的边BC上取一点D,使BD=AD即可;在右图△ABC中的边AC上取一点D,使BD=CD即可.
【答案与解析】
解:如图(1)所示:在BC上取一点D,使∠ADB=110°,∠ADC=70°,∠BAD=35°,∠CAD=40°,
/
如图(2)所示:在AC上取一点D,使∠ABD=32°,∠CBD=16°,∠ADB=32°,
/
∠BDC=148°.
【总结升华】本题考查了等腰三角形的性质和判定、三角形的内角和定理等知识点,关键是根据题意画出图形,注意应先确定等腰三角形的各个角的度数,再根据度数画出图形.
举一反三:
【变式】(2019?温州模拟)如图,有甲,乙两个三角形,请你用一条直线把每一个三角形分成两个等腰三角形,并标出每个三角形各角的度数.
/ /
【答案】解:如图1:直线把75°的角分成25°的角和50°的角,则分成的两个三角形都是等腰三角形;
如图2,直线把120°的角分成80°和40°的角,则分成的两个三角形都是等腰三角形.
/ /
类型三、等腰三角形性质与判定的综合应用
/3、(2019春?威海期末)在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.
/
【思路点拨】(1)连接BD由等腰三角形的性质和已知条件得出∠BAD=∠DAC=/×120°=60°,再由AD=AB,即可得出结论;
(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.
【答案与解析】
(1)证明:连接BD,
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=/∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=/×120°=60°,
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
/,
∴△BDE≌△ADF(ASA),
∴BE=AF.
/
【总结升华】本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
举一反三:
【变式】如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有 个.
/
【答案】4;
提示:根据等腰三角形的判定,由已知可证∠BAD=∠CAD=∠B=30°,即证△ADB是等腰三角形;又证CD=DE,AE=AC,即证△CDE,△AEC是等腰三角形;再证ECB=∠B=30°,即证△BEC是等腰三角形.即图中的等腰三角形共有4个.
/4、如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F,求证:CE=CF.
/
【思路点拨】根据三角形的内角和定理得出∠CAF+∠CFA=90°,∠FAD+∠AED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,根据等腰三角形的判定推出即可.
【答案与解析】
证明:∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF.
【总结升华】本题考查了直角三角形性质,等腰三角形的性质和判定,三角形的内角和定理,关键是推出∠CEF=∠CFE.
举一反三:
【变式】如图是由9个等边三角形拼成的六边形,现已知中间最小的等边三角形的边长是a,则围成的六边形的周长为( )
/
A. 30a B. 32a C. 34a D. 无法计算
【答案】A;
提示:设右下角第二个小的等边三角形的边长是x,则剩下的7个等边三角形的边长是x; x; x+a; x+a; x+2a ;x+2a; x+3a,根据题意得到方程2x=x+3a,求出x=3a,即可求出围成的六边形的周长.
类型四、含30°角的直角三角形
/5、如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然
后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13m,求旗杆AB的高.
/
【思路点拨】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD,再根据等角对等边的性质可得AD=CD,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
【答案与解析】
解:∵∠ACB=15°,∠ADB=30°, ∴∠CAD=∠ADB-∠ACB=30°-15°=15°, 即△CAD为等腰三角形, ∴AD=CD=13, 在△ADB中,∵AB⊥DB,∠ADB=30°, ∴AB=/AD=/×13=6.5(m).
【总结升华】本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,熟记性质是解题的关键.
举一反三:
【变式】已知:如图,在Rt△ABC中,∠C=90°,∠BAD=/∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=/DB.
/
【答案】
解:∵DE⊥AB, ∴∠AED=∠BED=90°, ∵DE是∠ADB的平分线, ∴∠3=∠4,又∵DE=DE, ∴△BED≌△AED(ASA), ∴AD=BD,∠2=∠B, ∵∠BAD=∠2=/∠BAC, ∴∠1=∠2=∠B, ∴AD=BD, 又∵∠1+∠2+∠B=90°, ∴∠B=∠1=∠2=30°, 在直角三角形ACD中,∠1=30°, ∴CD= /AD= /BD.
类型五、反证法
/6、求证:在一个三角形中,如果两个角不等,那么它们所对的边也不等.
【思路点拨】先假设它们的对边相等,然后根据等腰三角形的性质得出假设不成立,从而证得原结论成立.
【答案与解析】
证明:假设它们所对的边相等;
则根据等腰三角形的性质定理,“等边对等角”所以等它们所对的角也相等;
这就与题设两个角不等相矛盾;
因此假设不成立,故原结论成立.
【总结升华】本题结合等腰三角形的性质考查反证法,解此题关键要懂得反证法的意义及步骤.
举一反三:
【变式】用反证法证明“三角形三个内角中至少有两个锐角”时应首先假设
.
【答案】三角形三个内角中最多有一个锐角.
【巩固练习】
一.选择题
1.如图,在△ABC中,若AB=AC,BC=BD,AD=DE=EB,则∠A等于( ).
A.30° B.36° C.45° D.54°
/
2.用反证法证明:a,b至少有一个为0,应假设( )
A. a,b没有一个为0
B. a,b只有一个为0
C. a,b至多有一个为0
D. a,b两个都为0
3. 如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的有( )
①△BDF,△CEF都是等腰三角形; ②DE=DB+CE;
③AD+DE+AE=AB+AC; ④BF=CF. A.1个 B.2个 C.3个 D.4个
/
4. 等腰三角形一腰上的高与底边所成的角等于( )
A.顶角的一半 B.底角的一半 C.90°减去顶角的一半 D.90°减去底角的一半
5.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )
/
A./cm B.2cm C.3cm D.4cm
6. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
/
二.填空题
7.(2019?通辽)等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为 .
8. 用反证法证明“若|a|≠|b|,则a≠b.”时,应假设 .
9. 等腰三角形的周长为22/,其中一边的长是8/,则其余两边长分别为________.
10.(2019春?盐城校级月考)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,当t= 时,△ABD为等腰三角形.
/
11.如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF =_________°.
/
12. 如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
/ 三.解答题
13. 用反证法证明:一条线段只有一个中点.
14.(2019秋?宜昌期中)一个等腰三角形的三边长分别为x,2x﹣3,4x﹣6,求这个三角形的周长.
15.(2019秋?东台市期中)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
/
【答案与解析】
一.选择题
1. 【答案】C;
【解析】设∠A=/,则由题意∠ADE=180°-2/,∠EDB=/,∠BDC=∠BCD=90°-/,因为∠ADE+∠EDB+∠BDC=180°,所以/=45°.
2. 【答案】A;
【解析】由于命题:“a,b至少有一个为0”的反面是:“a,b没有一个为0”,故选A.
3. 【答案】C ;
【解析】①②③正确.
4. 【答案】A;
【解析】解:△ABC中,∵AB=AC,BD是高, ∴∠ABC=∠C=/ 在Rt△BDC中,∠CBD=90°-∠C=90°-/=/. 故选A.
/
5. 【答案】C;
【解析】解:∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm,
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm;
故选:C.
6. 【答案】D;
【解析】解:根据垂线段最短,可知AP的长不可小于3; ∵△ABC中,∠C=90°,AC=3,∠B=30°, ∴AB=6, ∴AP的长不能大于6. 故选D.
二.填空题
7. 【答案】69°或21°;
【解析】解:分两种情况讨论:
①若∠A<90°,如图1所示:
/
∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=48°,
∴∠A=90°﹣48°=42°,
∵AB=AC,
∴∠ABC=∠C=/(180°﹣42°)=69°;
②若∠A>90°,如图2所示:
/
同①可得:∠DAB=90°﹣48°=42°,
∴∠BAC=180°﹣42°=138°,
∵AB=AC,
∴∠ABC=∠C=/(180°﹣138°)=21°;
综上所述:等腰三角形底角的度数为69°或21°.
故答案为:69°或21°.
8. 【答案】a=b;
【解析】a,b的等价关系有a=b,a≠b两种情况,因而a≠b的反面是a=b.
9. 【答案】7/,7/或8/,6/;
【解析】边长为8cm的可能是底边,也可能是腰.
10.【答案】5,6,/;
【解析】解:在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm,由勾股定理得:AC=3cm,
由运动可知:AD=t,且△ABD时等腰三角形,
有三种情况:
①若AB=AD,则t=5;
②若BA=BD,则AD=2AC,即t=6;
③若DA=DB,则在Rt△BCD中,CD=t﹣3,BC=4,BD=t,
即(t﹣3)2+42=t2,
解得:t=/,
综合上述:符合要求的t值有3个,分别为5,6,/.
11.【答案】40;
【解析】AD=FD,∠FAD=∠AFD=70°,所以∠ADF=40°.
12.【答案】15°;
【解析】设∠A=/,∠BED=∠EBD=2/,∠CBD=120°-2/,∠C=∠BDC=30°+/,
而∠A+∠C=60°,所以/+30°+/ =60°,解得/=15°.
三.解答题
13.【解析】
已知:一条线段AB,M为AB的中点.
求证:线段AB只有一个中点M.
证明:假设线段AB有两个中点M、N,不妨设M在N的左边,
则AM<AN,
又因为AM=/AB=AN=/AB,
这与AM<AN矛盾,
所以线段AB只有一个中点M.
14.【解析】
解:①x=2x﹣3,则x=3,
∴4x﹣6=6,
∵3+3=6,
∴3、3、6不能构成三角形;
②x=4x﹣6,则x=2,
∴2x﹣3=1,
∵1、2、2任意两边之和大于第三边,
∴这个三角形的周长为1+2+2=5;
③2x﹣3=4x﹣6,则x=/,
∴2x﹣3=0,
∴此三角形不存在.
综上可知:这个三角形的周长为5.
15.【解析】
解:(1)∵∠C=90°,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴有勾股定理得PB=2/cm
∴△ABP的周长为:AP+PB+AB=6+10+2/=(16+2/)cm;
(2)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形;
(3)当P点在AC上,Q在AB上,则AP=8﹣t,AQ=16﹣2t,
∵直线PQ把△ABC的周长分成相等的两部分,
∴8﹣t+16﹣2t=12,
∴t=4;
当P点在AB上,Q在AC上,则AP=t﹣8,AQ=2t﹣16,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t﹣8+2t﹣16=12,
∴t=12,
∴当t为4或12秒时,直线PQ把△ABC的周长分成相等的两部分.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
