北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第4讲 角的平分线的性质(提高,附答案)
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第4讲 角的平分线的性质(提高,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-14 22:56:09 | ||
图片预览


文档简介
角的平分线的性质(提高)
【学习目标】
1.掌握角平分线的性质,理解三角形的三条角平分线的性质.
2.掌握角平分线的判定及角平分线的画法.
3. 熟练运用角的平分线的性质解决问题.
【要点梳理】
要点一、角的平分线的性质
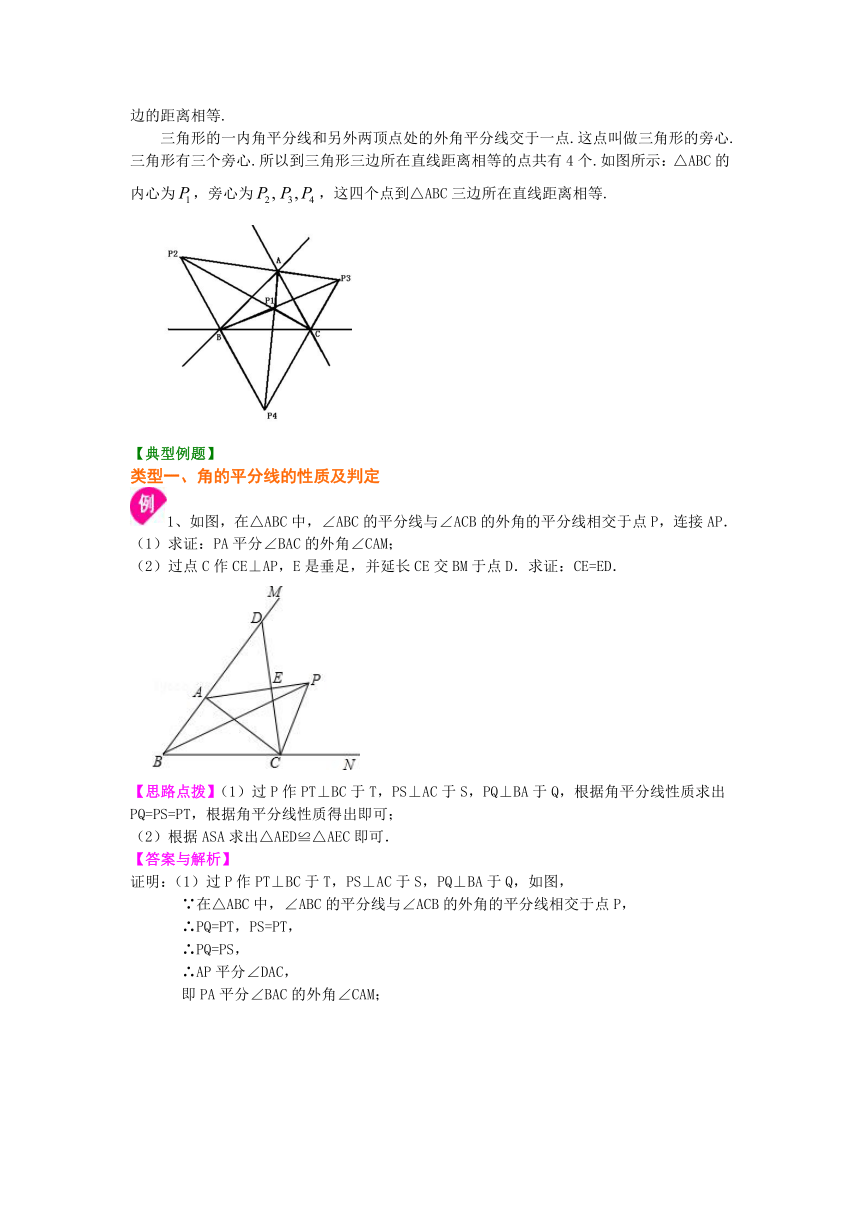
角的平分线的性质:角的平分线上的点到角两边的距离相等. 要点诠释: 用符号语言表示角的平分线的性质定理: 若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.
要点二、角的平分线的判定
角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.
要点诠释: 用符号语言表示角的平分线的判定: 若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB
要点三、角的平分线的尺规作图
角平分线的尺规作图
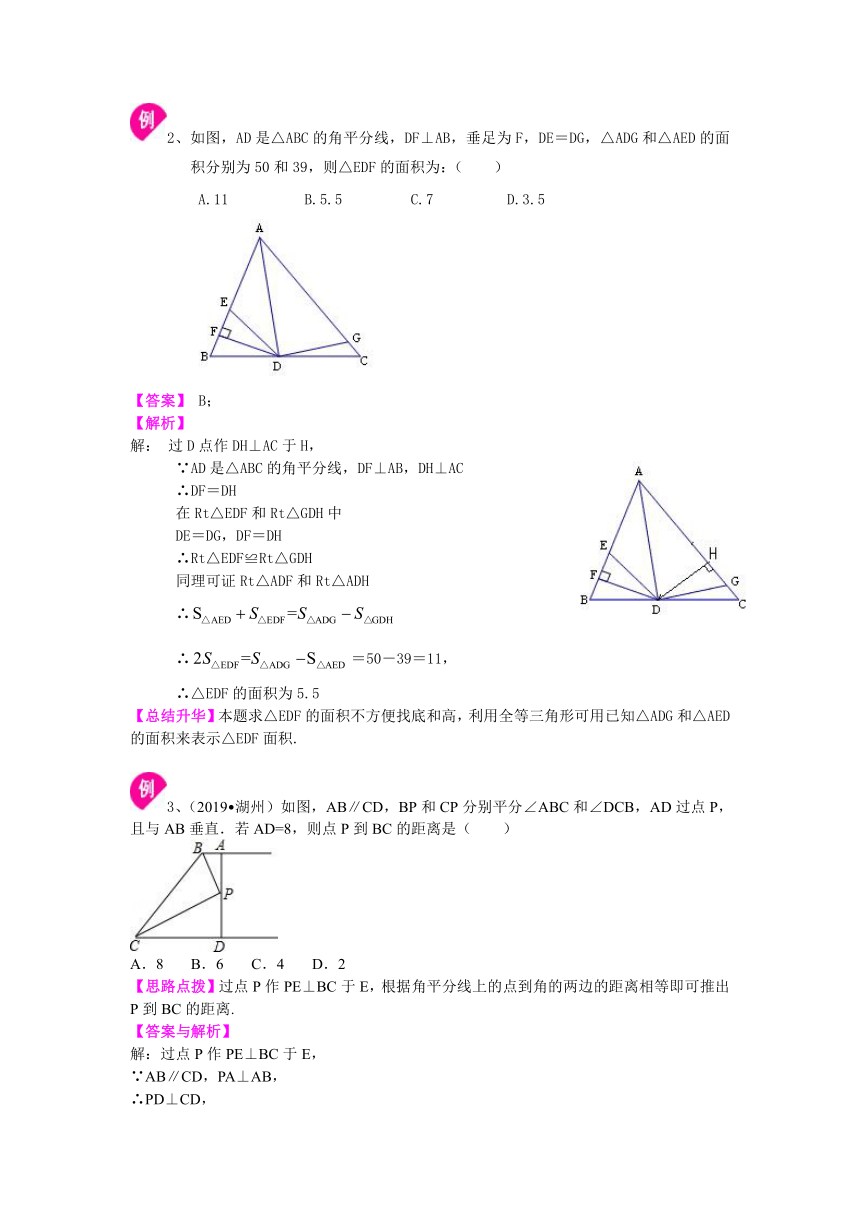
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E. (2)分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC.
射线OC即为所求.
要点四、三角形角平分线的性质
三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.
三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC的内心为,旁心为,这四个点到△ABC三边所在直线距离相等.
【典型例题】
类型一、角的平分线的性质及判定
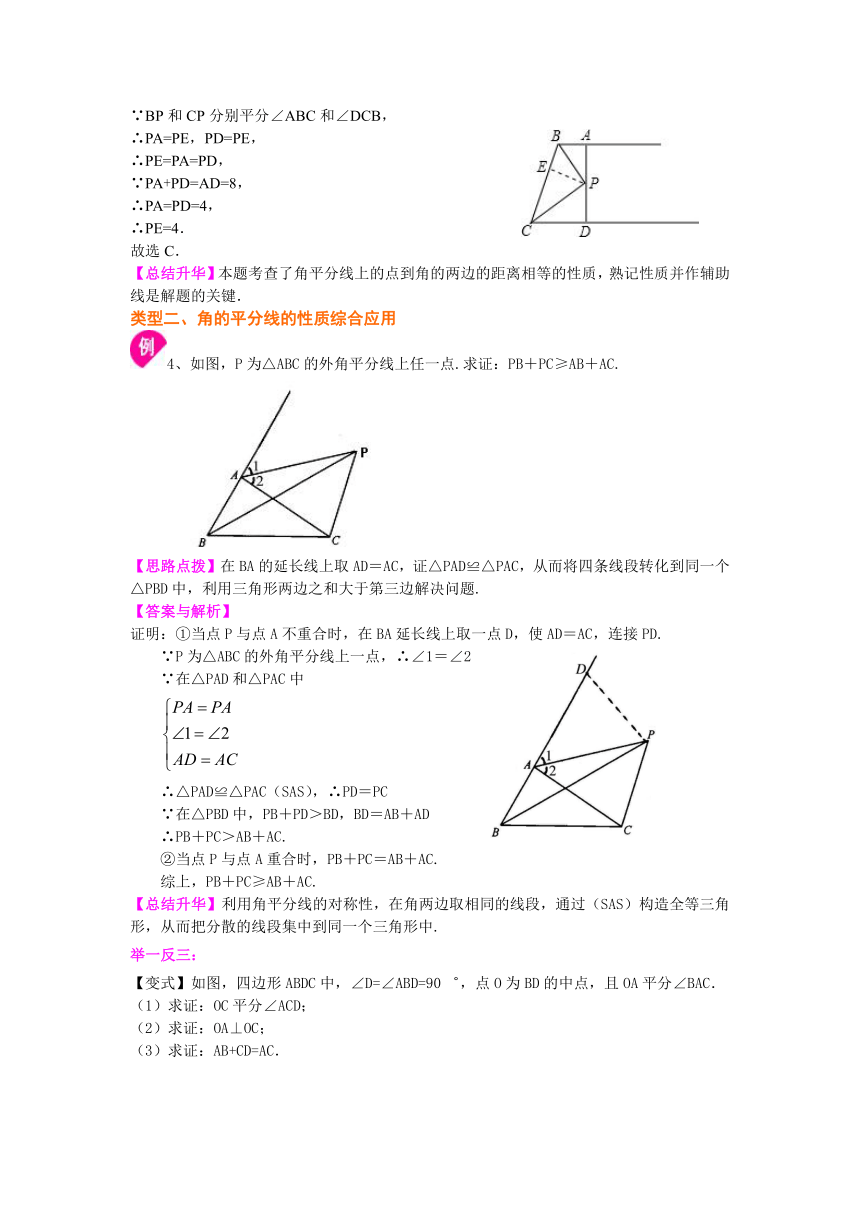
1、如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【思路点拨】(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;
(2)根据ASA求出△AED≌△AEC即可.
【答案与解析】
证明:(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM;
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
∴△AED≌△AEC,
∴CE=ED.
【总结升华】本题考查了角平分线性质和全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线并进一步求出PQ=PS和△AED≌△AEC,注意:角平分线上的点到角两边的距离相等.
举一反三:
【变式】如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F,且DB=DC.
求证:BE=CF.
【答案】
证明:∵DE⊥AE,DF⊥AC,AD是∠BAC的平分线,
∴DE=DF,∠BED=∠DFC=90°
在Rt△BDE与Rt△CDF中,,
∴Rt△BDE≌Rt△CDF(HL)
∴BE=CF
2、如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为:( )
A.11 B.5.5 C.7 D.3.5
【答案】 B;
【解析】
解: 过D点作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC
∴DF=DH
在Rt△EDF和Rt△GDH中
DE=DG,DF=DH
∴Rt△EDF≌Rt△GDH
同理可证Rt△ADF和Rt△ADH
∴
∴=50-39=11,
∴△EDF的面积为5.5
【总结升华】本题求△EDF的面积不方便找底和高,利用全等三角形可用已知△ADG和△AED的面积来表示△EDF面积.
3、(2019?湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
【思路点拨】过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等即可推出P到BC的距离.
【答案与解析】
解:过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
故选C.
【总结升华】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.
类型二、角的平分线的性质综合应用
4、如图,P为△ABC的外角平分线上任一点.求证:PB+PC≥AB+AC.
【思路点拨】在BA的延长线上取AD=AC,证△PAD≌△PAC,从而将四条线段转化到同一个△PBD中,利用三角形两边之和大于第三边解决问题.
【答案与解析】
证明:①当点P与点A不重合时,在BA延长线上取一点D,使AD=AC,连接PD.
∵P为△ABC的外角平分线上一点,∴∠1=∠2
∵在△PAD和△PAC中
∴△PAD≌△PAC(SAS),∴PD=PC
∵在△PBD中,PB+PD>BD,BD=AB+AD
∴PB+PC>AB+AC.
②当点P与点A重合时,PB+PC=AB+AC.
综上,PB+PC≥AB+AC.
【总结升华】利用角平分线的对称性,在角两边取相同的线段,通过(SAS)构造全等三角形,从而把分散的线段集中到同一个三角形中.
举一反三:
【变式】如图,四边形ABDC中,∠D=∠ABD=90゜,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
【答案】
证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
【巩固练习】
一.选择题
1. 已知,如图AD、BE是△ABC的两条高线,AD与BE交于点O,AD平分∠BAC,BE平分
∠ABC,下列结论:(1)CD=BD, (2)AE=CE (3)OA=OB=OD=OE (4)AE+BD=AB,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
2.(2019?招远市模拟)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
A.4 B.3 C.6 D.5
3. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB=( )
A.50° B.45° C.40° D .35°
4. 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S.若AQ=PQ,PR=PS,下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是( )
A.①③ B.②③ C.①② D.①②③
5.(2019春?成都校级期末)如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点 D.△ABC三条角平分线的交点
6.中,AD是的平分线,且.若,则 的大小为 ( )?
A. B. C. D.
二.填空题
7. 在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3.折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为 .
8. 如图,已知在中,平分,于,若,则的周长为 .
9.(2019?邯郸二模)如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
10.(2019春?海门市期末)如图△ABC中,AD平分∠BAC,AB=4,AC=2,且△ABD的面积为3,则△ACD的面积为 .
11.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______.
12. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB,D为AC上一点,若∠CBD=20°,则∠CED=__________.
三.解答题
13.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.
求证:CM=CN.
14.四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠ADC+∠B=180°
求证:2AE=AB+AD.
15.已知:如图,在ΔABC中,AD是△ABC的角平分线,E、F分别是AB、AC上一点,并且有∠EDF+∠EAF=180°.试判断DE和DF的大小关系并说明理由.
【答案与解析】
一.选择题
1.【答案】C;
【解析】(1)(2)(4)是正确的.
2.【答案】B;
【解析】解:过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,∴S△ABC=×4×2+AC×2=7,解得AC=3.故选:B.
3.【答案】B;
【解析】可证EA是∠CAB外角平分线.过点E作EF、EM、EN分别垂直于CB、AB、CA,并且交点分别为F、M、N,所以EF=EM=EN.所以EA是∠CAB的外角平分线.
4.【答案】C;
【解析】依据角平分线的判定定理知AP平分∠BAC,①正确,因AQ=PQ,∠PAQ=∠APQ=∠BAP,所以②正确.
5.【答案】D;
【解析】解:∵凉亭到草坪三条边的距离相等,
∴凉亭选择△ABC三条角平分线的交点.
故选D.
6.【答案】A;
【解析】在AB边上截取AE=AC,连接DE,可证△ACD≌△AED,可推出CD=DE=BE,
2∠B=∠C,所以∠B=40°.
二.填空题
7. 【答案】1;
【解析】由题意设DE=CE=,BC=BD=AD=,AE=2,AC =3=3,=1.
8. 【答案】15;
【解析】BC=CE+BE=AC+BE=AB+BE=AD+BD+BE=DE+BD+BE=15.
9. 【答案】30
【解析】解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=3,
∵△ABC的周长是22,OD⊥BC于D,且OD=3,
∴S△ABC=×AB×OE+×BC×OD+×AC×OF
=×(AB+BC+AC)×3
=20×3=30
10.【答案】;
【解析】解:过点D作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,
∴DE=DF,
∵AB=4,△ABD的面积为3,
∴S△ABD=AB?DE=×4×DE=3,解得DE=;
∴DF=,
∵AC=2,
∴S△ACD=AC?DF=×2×=.
故答案为:.
11.【答案】35°;
【解析】作EF⊥AD于F,证△DCE≌△DFE(HL),再证△AFE≌△ABE(HL),可得∠FEB=180°-70°=110°,∠AEB=55°,∠EAB=35°.
12.【答案】10°;
【解析】考虑△BDC中, EC 是∠C的平分线, EB是∠B的外角平分线, 所以E是△BDC的一个旁心, 于是ED平分∠BDA. ∠CED = ∠ADE - ∠DCE =∠ADB - ∠DCB =∠DBC = ×20°= 10°.
三.解答题
13.【解析】
证明:∵OD平分∠POQ
∴∠AOD=∠BOD
在△AOD与△BOD中
∴△AOD≌△BOD(SAS)
∴∠ADO=∠BDO
又∵CM⊥AD于M,CN⊥BD于N.
∴CM=CN(角平分线上的点到角两边的距离相等).
14.【解析】
证明:过C作CF⊥AD于F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠DFC=∠CEB=90°,
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵∠ADC+∠B=180°
∴∠FDC=∠EBC,
∴△FDC≌△EBC
∴DF=EB,
∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE
∴2AE=AB+AD
15.【解析】DE=DF.
证明:过点D作DM⊥AB于M,DN⊥AC于N,
∵AD是△ABC的角平分线,
∴DM=DN
∵∠EDF+∠EAF=180°,即∠2+∠3+∠4+∠EAF =180°
又∵∠1+∠2+∠3+∠EAF =180°
∴∠1=∠4
在Rt△DEM与Rt△DFN中
∴Rt△DEM≌Rt△DFN (ASA)
∴DE=DF
【学习目标】
1.掌握角平分线的性质,理解三角形的三条角平分线的性质.
2.掌握角平分线的判定及角平分线的画法.
3. 熟练运用角的平分线的性质解决问题.
【要点梳理】
要点一、角的平分线的性质
角的平分线的性质:角的平分线上的点到角两边的距离相等. 要点诠释: 用符号语言表示角的平分线的性质定理: 若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.
要点二、角的平分线的判定
角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.
要点诠释: 用符号语言表示角的平分线的判定: 若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB
要点三、角的平分线的尺规作图
角平分线的尺规作图
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E. (2)分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC.
射线OC即为所求.
要点四、三角形角平分线的性质
三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.
三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC的内心为,旁心为,这四个点到△ABC三边所在直线距离相等.
【典型例题】
类型一、角的平分线的性质及判定
1、如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【思路点拨】(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;
(2)根据ASA求出△AED≌△AEC即可.
【答案与解析】
证明:(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM;
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
∴△AED≌△AEC,
∴CE=ED.
【总结升华】本题考查了角平分线性质和全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线并进一步求出PQ=PS和△AED≌△AEC,注意:角平分线上的点到角两边的距离相等.
举一反三:
【变式】如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F,且DB=DC.
求证:BE=CF.
【答案】
证明:∵DE⊥AE,DF⊥AC,AD是∠BAC的平分线,
∴DE=DF,∠BED=∠DFC=90°
在Rt△BDE与Rt△CDF中,,
∴Rt△BDE≌Rt△CDF(HL)
∴BE=CF
2、如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为:( )
A.11 B.5.5 C.7 D.3.5
【答案】 B;
【解析】
解: 过D点作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC
∴DF=DH
在Rt△EDF和Rt△GDH中
DE=DG,DF=DH
∴Rt△EDF≌Rt△GDH
同理可证Rt△ADF和Rt△ADH
∴
∴=50-39=11,
∴△EDF的面积为5.5
【总结升华】本题求△EDF的面积不方便找底和高,利用全等三角形可用已知△ADG和△AED的面积来表示△EDF面积.
3、(2019?湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
【思路点拨】过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等即可推出P到BC的距离.
【答案与解析】
解:过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
故选C.
【总结升华】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.
类型二、角的平分线的性质综合应用
4、如图,P为△ABC的外角平分线上任一点.求证:PB+PC≥AB+AC.
【思路点拨】在BA的延长线上取AD=AC,证△PAD≌△PAC,从而将四条线段转化到同一个△PBD中,利用三角形两边之和大于第三边解决问题.
【答案与解析】
证明:①当点P与点A不重合时,在BA延长线上取一点D,使AD=AC,连接PD.
∵P为△ABC的外角平分线上一点,∴∠1=∠2
∵在△PAD和△PAC中
∴△PAD≌△PAC(SAS),∴PD=PC
∵在△PBD中,PB+PD>BD,BD=AB+AD
∴PB+PC>AB+AC.
②当点P与点A重合时,PB+PC=AB+AC.
综上,PB+PC≥AB+AC.
【总结升华】利用角平分线的对称性,在角两边取相同的线段,通过(SAS)构造全等三角形,从而把分散的线段集中到同一个三角形中.
举一反三:
【变式】如图,四边形ABDC中,∠D=∠ABD=90゜,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
【答案】
证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
【巩固练习】
一.选择题
1. 已知,如图AD、BE是△ABC的两条高线,AD与BE交于点O,AD平分∠BAC,BE平分
∠ABC,下列结论:(1)CD=BD, (2)AE=CE (3)OA=OB=OD=OE (4)AE+BD=AB,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
2.(2019?招远市模拟)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
A.4 B.3 C.6 D.5
3. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB=( )
A.50° B.45° C.40° D .35°
4. 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S.若AQ=PQ,PR=PS,下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是( )
A.①③ B.②③ C.①② D.①②③
5.(2019春?成都校级期末)如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点 D.△ABC三条角平分线的交点
6.中,AD是的平分线,且.若,则 的大小为 ( )?
A. B. C. D.
二.填空题
7. 在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3.折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为 .
8. 如图,已知在中,平分,于,若,则的周长为 .
9.(2019?邯郸二模)如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
10.(2019春?海门市期末)如图△ABC中,AD平分∠BAC,AB=4,AC=2,且△ABD的面积为3,则△ACD的面积为 .
11.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______.
12. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB,D为AC上一点,若∠CBD=20°,则∠CED=__________.
三.解答题
13.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.
求证:CM=CN.
14.四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠ADC+∠B=180°
求证:2AE=AB+AD.
15.已知:如图,在ΔABC中,AD是△ABC的角平分线,E、F分别是AB、AC上一点,并且有∠EDF+∠EAF=180°.试判断DE和DF的大小关系并说明理由.
【答案与解析】
一.选择题
1.【答案】C;
【解析】(1)(2)(4)是正确的.
2.【答案】B;
【解析】解:过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,∴S△ABC=×4×2+AC×2=7,解得AC=3.故选:B.
3.【答案】B;
【解析】可证EA是∠CAB外角平分线.过点E作EF、EM、EN分别垂直于CB、AB、CA,并且交点分别为F、M、N,所以EF=EM=EN.所以EA是∠CAB的外角平分线.
4.【答案】C;
【解析】依据角平分线的判定定理知AP平分∠BAC,①正确,因AQ=PQ,∠PAQ=∠APQ=∠BAP,所以②正确.
5.【答案】D;
【解析】解:∵凉亭到草坪三条边的距离相等,
∴凉亭选择△ABC三条角平分线的交点.
故选D.
6.【答案】A;
【解析】在AB边上截取AE=AC,连接DE,可证△ACD≌△AED,可推出CD=DE=BE,
2∠B=∠C,所以∠B=40°.
二.填空题
7. 【答案】1;
【解析】由题意设DE=CE=,BC=BD=AD=,AE=2,AC =3=3,=1.
8. 【答案】15;
【解析】BC=CE+BE=AC+BE=AB+BE=AD+BD+BE=DE+BD+BE=15.
9. 【答案】30
【解析】解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=3,
∵△ABC的周长是22,OD⊥BC于D,且OD=3,
∴S△ABC=×AB×OE+×BC×OD+×AC×OF
=×(AB+BC+AC)×3
=20×3=30
10.【答案】;
【解析】解:过点D作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,
∴DE=DF,
∵AB=4,△ABD的面积为3,
∴S△ABD=AB?DE=×4×DE=3,解得DE=;
∴DF=,
∵AC=2,
∴S△ACD=AC?DF=×2×=.
故答案为:.
11.【答案】35°;
【解析】作EF⊥AD于F,证△DCE≌△DFE(HL),再证△AFE≌△ABE(HL),可得∠FEB=180°-70°=110°,∠AEB=55°,∠EAB=35°.
12.【答案】10°;
【解析】考虑△BDC中, EC 是∠C的平分线, EB是∠B的外角平分线, 所以E是△BDC的一个旁心, 于是ED平分∠BDA. ∠CED = ∠ADE - ∠DCE =∠ADB - ∠DCB =∠DBC = ×20°= 10°.
三.解答题
13.【解析】
证明:∵OD平分∠POQ
∴∠AOD=∠BOD
在△AOD与△BOD中
∴△AOD≌△BOD(SAS)
∴∠ADO=∠BDO
又∵CM⊥AD于M,CN⊥BD于N.
∴CM=CN(角平分线上的点到角两边的距离相等).
14.【解析】
证明:过C作CF⊥AD于F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠DFC=∠CEB=90°,
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵∠ADC+∠B=180°
∴∠FDC=∠EBC,
∴△FDC≌△EBC
∴DF=EB,
∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE
∴2AE=AB+AD
15.【解析】DE=DF.
证明:过点D作DM⊥AB于M,DN⊥AC于N,
∵AD是△ABC的角平分线,
∴DM=DN
∵∠EDF+∠EAF=180°,即∠2+∠3+∠4+∠EAF =180°
又∵∠1+∠2+∠3+∠EAF =180°
∴∠1=∠4
在Rt△DEM与Rt△DFN中
∴Rt△DEM≌Rt△DFN (ASA)
∴DE=DF
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
