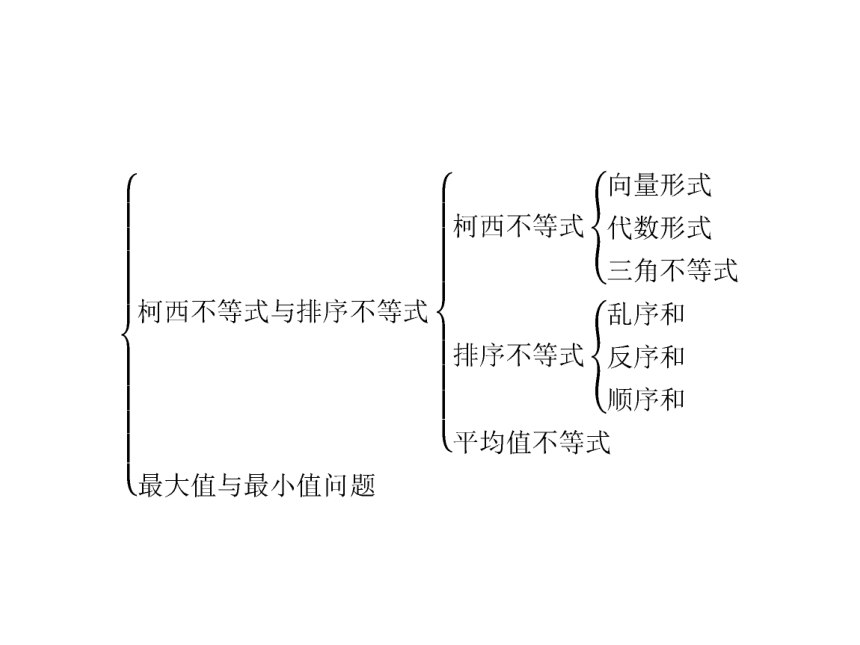
高中数学选修4-5第二章柯西不等式与排序不等式及其应用本章整合2:18张PPT
文档属性
| 名称 | 高中数学选修4-5第二章柯西不等式与排序不等式及其应用本章整合2:18张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 00:00:00 | ||
图片预览


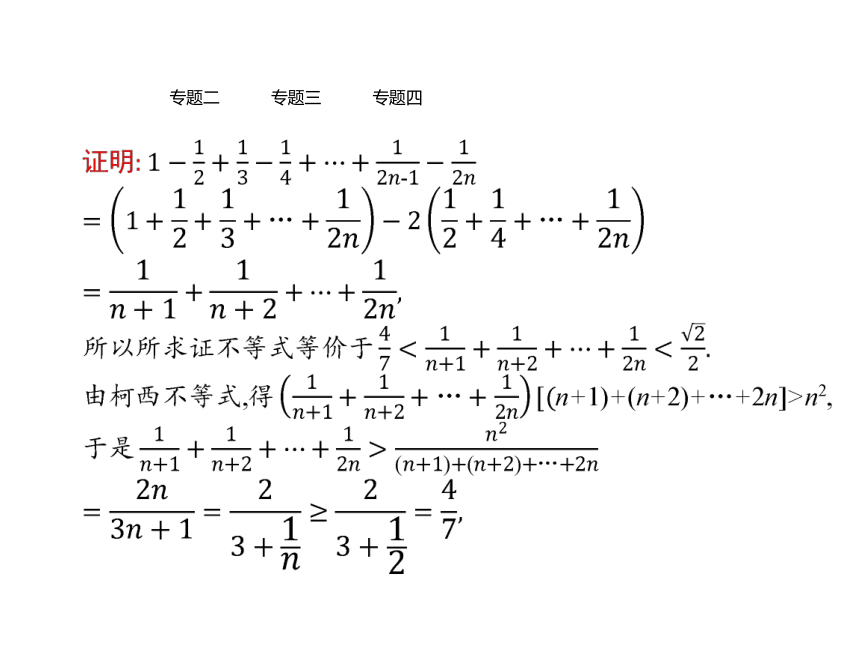




文档简介
课件18张PPT。专题一专题二专题三专题四专题一 柯西不等式的应用
利用柯西不等式证明其他不等式或求最值,关键是构造两组数,并向着柯西不等式的形式进行转化.
应用若n是不小于2的正整数,试证:提示:注意中间的一列数的代数和,其奇数项为正,偶数项为负,可进行恒等变形予以化简.专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四专题二 排序不等式的应用
应用排序不等式可以简捷地证明一类不等式,其证明的关键是找出两组有序数组,通常可以根据函数的单调性去寻找.
应用设0∴ln a1≤ln a2≤…≤ln an.
又∵0≤b1≤b2≤…≤bn,
∴由排序不等式可知b1ln a1+b2ln a2+…+bnln an
≥c1ln a1+c2ln a2+…+cnln an
≥bnln a1+bn-1ln a2+…+b1ln an.专题一专题二专题三专题四专题一专题二专题三专题四专题三 最值问题
有关不等式问题往往要涉及对式子或量的范围的限定.其中含有多变量限制条件的最值问题往往难以处理,在这类问题中,利用柯西不等式或排序不等式求解较容易.但在求最值时,无论是应用柯西不等式,还是排序不等式、平均值不等式,都应该注意等号成立的条件.专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四应用2已知正实数x1,x2,…,xn满足x1+x2+…+xn=P,P为定值, 专题一专题二专题三专题四专题四 求参数的取值范围问题
应用不等式的知识,可以十分巧妙地解决一类求参数的取值范围问题.专题一专题二专题三专题四应用1求使lg(xy)≤ 对大于1的任意x与y恒成立的a的取值范围.专题一专题二专题三专题四应用2设f(x)是定义在[-1,1]上的奇函数,且对任意a,b∈[-1,1],当a+b≠0时,都
(1)若a>b,试比较f(a)与f(b)的大小;(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集为空集,求c的取值范围.
提示:本题的(1)(2)两问密切相关,都应由已知不等式推出函数的单调性,以便解决问题.专题一专题二专题三专题四解:(1)设x1,x2是[-1,1]上的任意两个实数,且x1f(x1),即f(x)在[-1,1]上是增函数.
∴当-1≤bf(b).
(2)∵f(x)在[-1,1]上是增函数,专题一专题二专题三专题四(3)设g(x)的定义域为P,h(x)的定义域为Q,
则P={x|-1≤x-c≤1}={x|c-1≤x≤1+c},
Q={x|-1≤x-c2≤1}={x|c2-1≤x≤1+c2}.
若P∩Q=?,必有c+1而c2-c-2>0?c>2或c<-1,
c2-c+2<0?c∈?.
故c的取值范围是(-∞,-1)∪(2,+∞).12122(湖南高考)已知a,b,c∈R,a+2b+3c=6,则a2+4b2+9c2的最小值为 .?
解析:由柯西不等式,得(12+12+12)(a2+4b2+9c2)≥(a+2b+3c)2,即a2+4b2+9c2≥12,当a=2b=3c=2时等号成立,所以a2+4b2+9c2的最小值为12.
答案:12
利用柯西不等式证明其他不等式或求最值,关键是构造两组数,并向着柯西不等式的形式进行转化.
应用若n是不小于2的正整数,试证:提示:注意中间的一列数的代数和,其奇数项为正,偶数项为负,可进行恒等变形予以化简.专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四专题二 排序不等式的应用
应用排序不等式可以简捷地证明一类不等式,其证明的关键是找出两组有序数组,通常可以根据函数的单调性去寻找.
应用设0
又∵0≤b1≤b2≤…≤bn,
∴由排序不等式可知b1ln a1+b2ln a2+…+bnln an
≥c1ln a1+c2ln a2+…+cnln an
≥bnln a1+bn-1ln a2+…+b1ln an.专题一专题二专题三专题四专题一专题二专题三专题四专题三 最值问题
有关不等式问题往往要涉及对式子或量的范围的限定.其中含有多变量限制条件的最值问题往往难以处理,在这类问题中,利用柯西不等式或排序不等式求解较容易.但在求最值时,无论是应用柯西不等式,还是排序不等式、平均值不等式,都应该注意等号成立的条件.专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四专题一专题二专题三专题四应用2已知正实数x1,x2,…,xn满足x1+x2+…+xn=P,P为定值, 专题一专题二专题三专题四专题四 求参数的取值范围问题
应用不等式的知识,可以十分巧妙地解决一类求参数的取值范围问题.专题一专题二专题三专题四应用1求使lg(xy)≤ 对大于1的任意x与y恒成立的a的取值范围.专题一专题二专题三专题四应用2设f(x)是定义在[-1,1]上的奇函数,且对任意a,b∈[-1,1],当a+b≠0时,都
(1)若a>b,试比较f(a)与f(b)的大小;(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集为空集,求c的取值范围.
提示:本题的(1)(2)两问密切相关,都应由已知不等式推出函数的单调性,以便解决问题.专题一专题二专题三专题四解:(1)设x1,x2是[-1,1]上的任意两个实数,且x1
∴当-1≤b
(2)∵f(x)在[-1,1]上是增函数,专题一专题二专题三专题四(3)设g(x)的定义域为P,h(x)的定义域为Q,
则P={x|-1≤x-c≤1}={x|c-1≤x≤1+c},
Q={x|-1≤x-c2≤1}={x|c2-1≤x≤1+c2}.
若P∩Q=?,必有c+1
c2-c+2<0?c∈?.
故c的取值范围是(-∞,-1)∪(2,+∞).12122(湖南高考)已知a,b,c∈R,a+2b+3c=6,则a2+4b2+9c2的最小值为 .?
解析:由柯西不等式,得(12+12+12)(a2+4b2+9c2)≥(a+2b+3c)2,即a2+4b2+9c2≥12,当a=2b=3c=2时等号成立,所以a2+4b2+9c2的最小值为12.
答案:12
