人教版九年级数学上册第二十四章圆24.3正多边形和圆学案设计
文档属性
| 名称 | 人教版九年级数学上册第二十四章圆24.3正多边形和圆学案设计 | 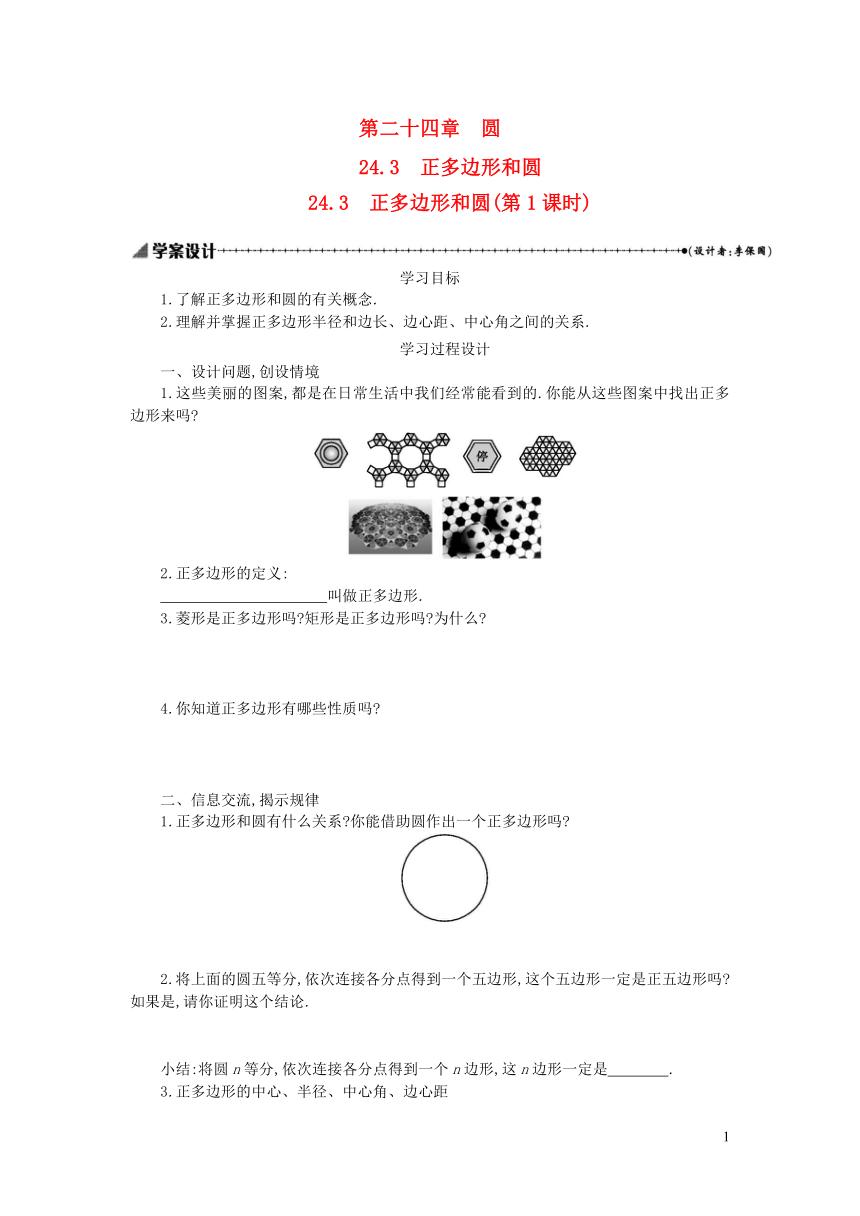 | |
| 格式 | zip | ||
| 文件大小 | 266.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-15 18:43:42 | ||
图片预览


文档简介
第二十四章 圆
24.3 正多边形和圆
24.3 正多边形和圆(第1课时)
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
学习过程设计
一、设计问题,创设情境
1.这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出正多边形来吗?
2.正多边形的定义:
叫做正多边形.?
3.菱形是正多边形吗?矩形是正多边形吗?为什么?
4.你知道正多边形有哪些性质吗?
二、信息交流,揭示规律
1.正多边形和圆有什么关系?你能借助圆作出一个正多边形吗?
2.将上面的圆五等分,依次连接各分点得到一个五边形,这个五边形一定是正五边形吗?如果是,请你证明这个结论.
小结:将圆n等分,依次连接各分点得到一个n边形,这n边形一定是 .?
3.正多边形的中心、半径、中心角、边心距
我们把一个正多边形的外接圆的圆心叫做正多边形的 .外接圆的半径叫做正多边形的 .正多边形每一边所对的圆心角叫做正多边形的 .中心到正多边形的一边的距离叫做正多边形的 .?
三、运用规律,解决问题
【例1】 有一个亭子(如图)它的地基是半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
四、变式训练,深化提高
【例2】 如图,分别求半径为R的圆的内接正三角形、正方形的边长、边心距和面积.
图①
图②
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.正三角形、正方形、正五边形、正六边形.
2.各边相等、各角也相等的多边形
3.不是.菱形各角不都相等;矩形各边不都相等.
4.各边相等,各角相等.
二、信息交流,揭示规律
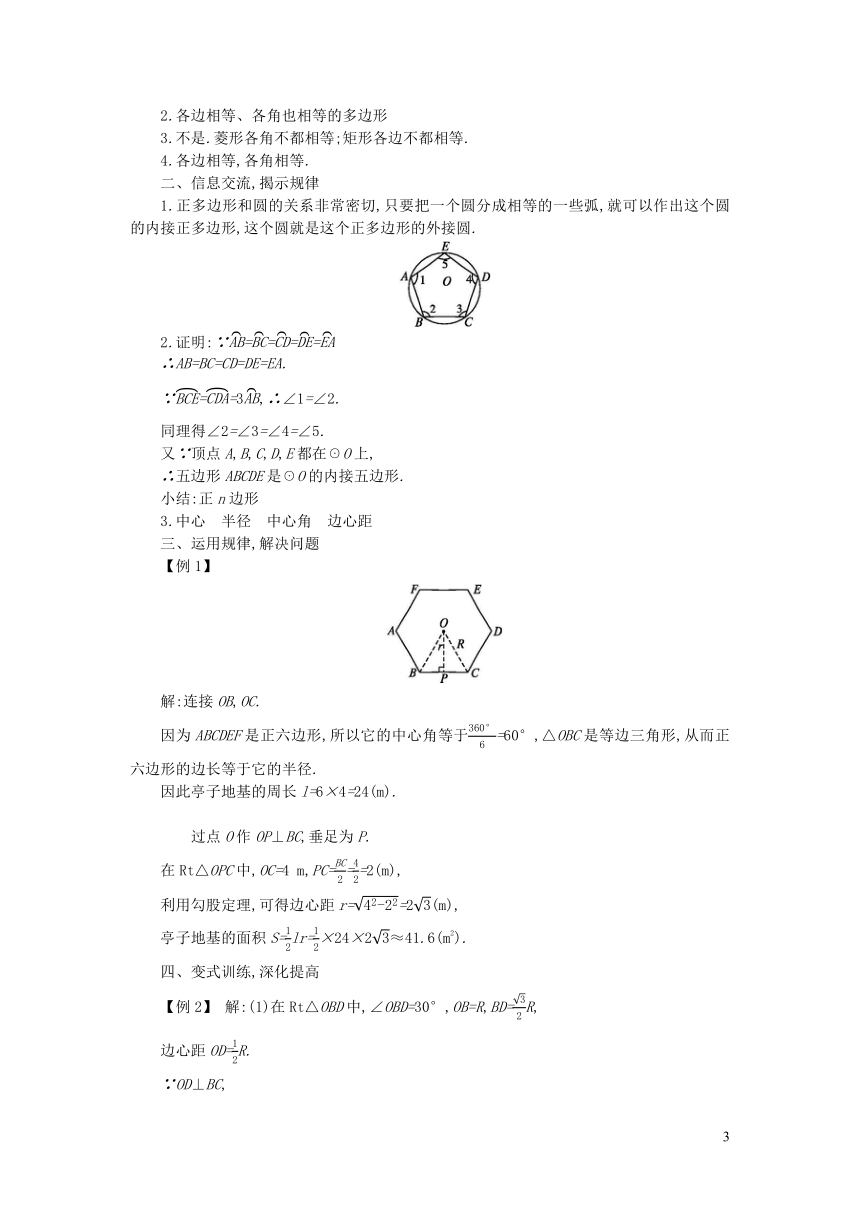
1.正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.证明:∵====
∴AB=BC=CD=DE=EA.
∵==3,∴∠1=∠2.
同理得∠2=∠3=∠4=∠5.
又∵顶点A,B,C,D,E都在☉O上,
∴五边形ABCDE是☉O的内接五边形.
小结:正n边形
3.中心 半径 中心角 边心距
三、运用规律,解决问题
【例1】
解:连接OB,OC.
因为ABCDEF是正六边形,所以它的中心角等于=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此亭子地基的周长l=6×4=24(m).
过点O作OP⊥BC,垂足为P.
在Rt△OPC中,OC=4 m,PC===2(m),
利用勾股定理,可得边心距r==2(m),
亭子地基的面积S=lr=×24×2≈41.6(m2).
四、变式训练,深化提高
【例2】 解:(1)在Rt△OBD中,∠OBD=30°,OB=R,BD=R,
边心距OD=R.
∵OD⊥BC,
∴BC=2BD=R,
∴S△ABC=3×BC·OD=3×·R·R=R2.
(2)在Rt△OBE中,∠OBE=45°,OB=R,
∴边心距OE=BE=R.
∵OE⊥BC,
∴BC=2BE=R,
∴S=4×BC·OE=4×·R·R=2R2.
五、反思小结,观点提炼
略
第二十四章 圆
24.3 正多边形和圆
24.3 正多边形和圆(第2课时)
学习目标
1.进一步理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
2.掌握圆内接正多边形的两种画法:
(1)用量角器等分圆周法作正多边形;
(2)用尺规作图法作特殊的正多边形.
教学过程设计
一、设计问题,创设情境
旧知巩固
1.什么叫做正多边形?什么是正多边形的边长、中心、半径、边心距、中心角?
2.正多边形和圆有怎样的关系?
3.正n边形的一个内角的度数是 ;中心角是 ;中心角和外角的关系是 .?
二、信息交流,揭示规律
1.怎样等分圆周?
2.你能用等分圆周的方法画出边长为2 cm的正六边形吗?
小结:等分圆周的方法: .?
三、运用规律,解决问题
1.请用上面的方法画出半径为2 cm☉O的内接正三角形;
2.你能用尺规作图法作出☉O的内接正四边形、正五边形吗?
3.你能用尺规作图法作出☉O的内接正四边形、正八边形吗?
四、变式训练,深化提高
方案设计
学校在教学楼前的圆形广场中,准备建造一个花园,并在花园内分别种植牡丹、月季和杜鹃三种花卉.为了美观,种植要求如下:
(1)种植4块面积相等的牡丹、4块面积相等的月季和一块杜鹃.(注意:面积相等必须由数学知识作保证)
(2)花卉总面积等于广场面积
(3)花园边界只能种植牡丹花,杜鹃花种植在花园中间且与牡丹花没有公共边.
请你设计种植方案.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.(1)各边相等,各角也相等的多边形叫做正多边形;正多边形的中心:一个正多边形的外接圆的圆心;正多边形的半径:外接圆的半径;正多边形的中心角:正多边形的每一边所对的圆心角;正多边形的边心距:中心到正多边形的一边的距离.
(2)正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
(3);;相等.
2.因为同圆中相等的圆心角所对的弧相等,所以作相等的圆心角就可以等分圆,从而得到相应的正多边形.
二、信息交流,揭示规律
1.略.
2.第一种方法,如图,以2 cm为半径作一个☉O,用量角器画一个等于60°的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
第二种方法,先用量角器画一个圆心角,然后在圆上依次截取等于该圆心角所对弧的等弧,于是得到圆的等分点.
小结:作圆确定圆心角所对的弧截取等弧顺次连接各分点正多边形.
三、运用规律,解决问题
1,2图略
3.只要作出已知☉O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与☉O相交,或作各中心角的角平分线与☉O相交,即得圆内接正八边形.
四、变式训练,深化提高
方案设计
五、反思小结,观点提炼
略
1
24.3 正多边形和圆
24.3 正多边形和圆(第1课时)
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
学习过程设计
一、设计问题,创设情境
1.这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出正多边形来吗?
2.正多边形的定义:
叫做正多边形.?
3.菱形是正多边形吗?矩形是正多边形吗?为什么?
4.你知道正多边形有哪些性质吗?
二、信息交流,揭示规律
1.正多边形和圆有什么关系?你能借助圆作出一个正多边形吗?
2.将上面的圆五等分,依次连接各分点得到一个五边形,这个五边形一定是正五边形吗?如果是,请你证明这个结论.
小结:将圆n等分,依次连接各分点得到一个n边形,这n边形一定是 .?
3.正多边形的中心、半径、中心角、边心距
我们把一个正多边形的外接圆的圆心叫做正多边形的 .外接圆的半径叫做正多边形的 .正多边形每一边所对的圆心角叫做正多边形的 .中心到正多边形的一边的距离叫做正多边形的 .?
三、运用规律,解决问题
【例1】 有一个亭子(如图)它的地基是半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
四、变式训练,深化提高
【例2】 如图,分别求半径为R的圆的内接正三角形、正方形的边长、边心距和面积.
图①
图②
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.正三角形、正方形、正五边形、正六边形.
2.各边相等、各角也相等的多边形
3.不是.菱形各角不都相等;矩形各边不都相等.
4.各边相等,各角相等.
二、信息交流,揭示规律
1.正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.证明:∵====
∴AB=BC=CD=DE=EA.
∵==3,∴∠1=∠2.
同理得∠2=∠3=∠4=∠5.
又∵顶点A,B,C,D,E都在☉O上,
∴五边形ABCDE是☉O的内接五边形.
小结:正n边形
3.中心 半径 中心角 边心距
三、运用规律,解决问题
【例1】
解:连接OB,OC.
因为ABCDEF是正六边形,所以它的中心角等于=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此亭子地基的周长l=6×4=24(m).
过点O作OP⊥BC,垂足为P.
在Rt△OPC中,OC=4 m,PC===2(m),
利用勾股定理,可得边心距r==2(m),
亭子地基的面积S=lr=×24×2≈41.6(m2).
四、变式训练,深化提高
【例2】 解:(1)在Rt△OBD中,∠OBD=30°,OB=R,BD=R,
边心距OD=R.
∵OD⊥BC,
∴BC=2BD=R,
∴S△ABC=3×BC·OD=3×·R·R=R2.
(2)在Rt△OBE中,∠OBE=45°,OB=R,
∴边心距OE=BE=R.
∵OE⊥BC,
∴BC=2BE=R,
∴S=4×BC·OE=4×·R·R=2R2.
五、反思小结,观点提炼
略
第二十四章 圆
24.3 正多边形和圆
24.3 正多边形和圆(第2课时)
学习目标
1.进一步理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
2.掌握圆内接正多边形的两种画法:
(1)用量角器等分圆周法作正多边形;
(2)用尺规作图法作特殊的正多边形.
教学过程设计
一、设计问题,创设情境
旧知巩固
1.什么叫做正多边形?什么是正多边形的边长、中心、半径、边心距、中心角?
2.正多边形和圆有怎样的关系?
3.正n边形的一个内角的度数是 ;中心角是 ;中心角和外角的关系是 .?
二、信息交流,揭示规律
1.怎样等分圆周?
2.你能用等分圆周的方法画出边长为2 cm的正六边形吗?
小结:等分圆周的方法: .?
三、运用规律,解决问题
1.请用上面的方法画出半径为2 cm☉O的内接正三角形;
2.你能用尺规作图法作出☉O的内接正四边形、正五边形吗?
3.你能用尺规作图法作出☉O的内接正四边形、正八边形吗?
四、变式训练,深化提高
方案设计
学校在教学楼前的圆形广场中,准备建造一个花园,并在花园内分别种植牡丹、月季和杜鹃三种花卉.为了美观,种植要求如下:
(1)种植4块面积相等的牡丹、4块面积相等的月季和一块杜鹃.(注意:面积相等必须由数学知识作保证)
(2)花卉总面积等于广场面积
(3)花园边界只能种植牡丹花,杜鹃花种植在花园中间且与牡丹花没有公共边.
请你设计种植方案.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.(1)各边相等,各角也相等的多边形叫做正多边形;正多边形的中心:一个正多边形的外接圆的圆心;正多边形的半径:外接圆的半径;正多边形的中心角:正多边形的每一边所对的圆心角;正多边形的边心距:中心到正多边形的一边的距离.
(2)正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
(3);;相等.
2.因为同圆中相等的圆心角所对的弧相等,所以作相等的圆心角就可以等分圆,从而得到相应的正多边形.
二、信息交流,揭示规律
1.略.
2.第一种方法,如图,以2 cm为半径作一个☉O,用量角器画一个等于60°的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
第二种方法,先用量角器画一个圆心角,然后在圆上依次截取等于该圆心角所对弧的等弧,于是得到圆的等分点.
小结:作圆确定圆心角所对的弧截取等弧顺次连接各分点正多边形.
三、运用规律,解决问题
1,2图略
3.只要作出已知☉O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与☉O相交,或作各中心角的角平分线与☉O相交,即得圆内接正八边形.
四、变式训练,深化提高
方案设计
五、反思小结,观点提炼
略
1
同课章节目录
