人教版九年级数学上册第二十三章旋转数学活动学案设计含答案
文档属性
| 名称 | 人教版九年级数学上册第二十三章旋转数学活动学案设计含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 104.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-15 22:19:27 | ||
图片预览

文档简介
第二十三章 旋转
数学活动
学习目标
1.加深对中心对称的理解.
2.能够在直角坐标系中,将图形进行中心对称变换.
学习过程
一、自主思考
1.什么是图形的旋转,旋转中心以及旋转角?
2.什么是中心对称,中心对称图形?
3.中心对称与轴对称的区别是什么?
二、学习新知
活动1:如图,在平面直角坐标系中选一点A(-3,2),作点A关于x轴的对称点,得到点B,作点B关于y轴的对称点,得到点C.点A与点C有什么关系?你是怎么得到的?将点A的坐标换成其他的数值还成立吗?
活动2:(1)把点P(x,y)绕原点分别顺时针旋转90°,180°,270°,360°,点P的对应点的坐标分别是什么?将结果填入下表:
旋转的角度 90° 180° 270° 360°
对应点的坐标
(2)如果是逆时针方向旋转呢?
活动3:如图,先准备一个花瓣模板,再选一点作为花心,然后围绕花心旋转花瓣模板,(强调画出的花要均匀)你画的是几瓣花?经过几次旋转?每一次的旋转角度是多少?
三、课堂练习
1.正方形绕中心至少旋转 后能与自身重合.?
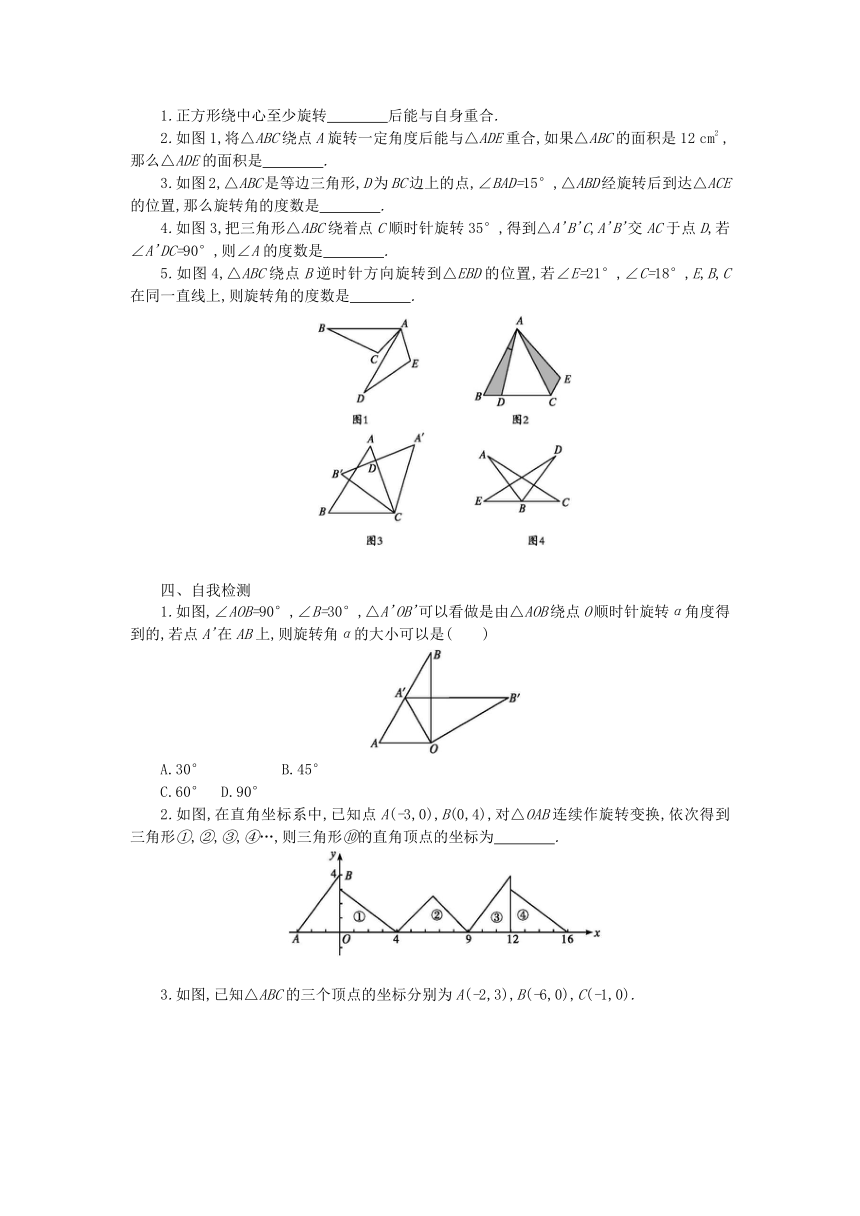
2.如图1,将△ABC绕点A旋转一定角度后能与△ADE重合,如果△ABC的面积是12 cm2 ,那么△ADE的面积是 .?
3.如图2,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,△ABD经旋转后到达△ACE的位置,那么旋转角的度数是 .?
4.如图3,把三角形△ABC绕着点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是 .?
5.如图4,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠E=21°,∠C=18°,E,B,C在同一直线上,则旋转角的度数是 .?
四、自我检测
1.如图,∠AOB=90°,∠B=30°,△A'OB'可以看做是由△AOB绕点O顺时针旋转α角度得到的,若点A'在AB上,则旋转角α的大小可以是( )
A.30° B.45°
C.60° D.90°
2.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 .?
3.如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)请直接写出点A关于y轴对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
布置作业
1.必做题:课本第74页数学活动活动1.
2.选做题:课本第74页数学活动活动2.
参考答案
一、自主思考
1.略 2.略
3.
轴对称 中心对称
定义 两个图形如果沿着某条直线对折,直线两旁的部分能够互相重合,则这两个图形关于这条直线轴对称 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
定义 三要点 1.有一条对称轴——直线; 2.图形沿轴对折,即翻转180度; 3.翻转后与另一图形重合 1.有一个对称中心——点; 2.图形绕中心旋转180°; 3.旋转后与另一图形重合
性质 1.两个图形是全等图形 1.两个图形是全等图形
2.对称轴是对应点连线的垂直平分线 2.对称中心到对应点的距离相等
3.对应线段或延长线相交,交点在对称轴上 3.对应点与对称中心在同一条直线上
二、学习新知
活动1:求出:B(-3,-2),C(3,-2),连接AC可以发现它们过O点, A点与C点是关于点O成中心对称的,进一步观察它们的坐标可以发现它们的坐标特点:
关于原点对称的点的坐标变换法则:横纵坐标变为原来的相反数.
活动2:(1)
旋转的角度 90° 180° 270° 360°
对应点的坐标 (y,-x) (-x,-y) (-y,x) (x,y)
(2)略
活动3:在上述实验中,不管通过做几次旋转都可以画出一朵花,设为n,则旋转的角度为.
三、课堂练习
1. 90°
2.12 cm2
3.60°
4.55°
5.39°
四、自我检测
1.C 解析:∵∠AOB=90°,∠B=30°,
∴∠A=60°.
又∵OA=OA',
∴△AOA'是等边三角形.
∴∠AOA'=60°,即旋转角α为60°.故选C.
2.(36,0) 解析:∵每三次变换为一个循环,∴三角形⑩的直角顶点的横坐标为12×3=36.
3.(1)(2,3);
(2)图形略,(0,-6);
(3)(-7,3)或(-5,-3)或(3,3).
数学活动
学习目标
1.加深对中心对称的理解.
2.能够在直角坐标系中,将图形进行中心对称变换.
学习过程
一、自主思考
1.什么是图形的旋转,旋转中心以及旋转角?
2.什么是中心对称,中心对称图形?
3.中心对称与轴对称的区别是什么?
二、学习新知
活动1:如图,在平面直角坐标系中选一点A(-3,2),作点A关于x轴的对称点,得到点B,作点B关于y轴的对称点,得到点C.点A与点C有什么关系?你是怎么得到的?将点A的坐标换成其他的数值还成立吗?
活动2:(1)把点P(x,y)绕原点分别顺时针旋转90°,180°,270°,360°,点P的对应点的坐标分别是什么?将结果填入下表:
旋转的角度 90° 180° 270° 360°
对应点的坐标
(2)如果是逆时针方向旋转呢?
活动3:如图,先准备一个花瓣模板,再选一点作为花心,然后围绕花心旋转花瓣模板,(强调画出的花要均匀)你画的是几瓣花?经过几次旋转?每一次的旋转角度是多少?
三、课堂练习
1.正方形绕中心至少旋转 后能与自身重合.?
2.如图1,将△ABC绕点A旋转一定角度后能与△ADE重合,如果△ABC的面积是12 cm2 ,那么△ADE的面积是 .?
3.如图2,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,△ABD经旋转后到达△ACE的位置,那么旋转角的度数是 .?
4.如图3,把三角形△ABC绕着点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是 .?
5.如图4,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠E=21°,∠C=18°,E,B,C在同一直线上,则旋转角的度数是 .?
四、自我检测
1.如图,∠AOB=90°,∠B=30°,△A'OB'可以看做是由△AOB绕点O顺时针旋转α角度得到的,若点A'在AB上,则旋转角α的大小可以是( )
A.30° B.45°
C.60° D.90°
2.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 .?
3.如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)请直接写出点A关于y轴对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
布置作业
1.必做题:课本第74页数学活动活动1.
2.选做题:课本第74页数学活动活动2.
参考答案
一、自主思考
1.略 2.略
3.
轴对称 中心对称
定义 两个图形如果沿着某条直线对折,直线两旁的部分能够互相重合,则这两个图形关于这条直线轴对称 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
定义 三要点 1.有一条对称轴——直线; 2.图形沿轴对折,即翻转180度; 3.翻转后与另一图形重合 1.有一个对称中心——点; 2.图形绕中心旋转180°; 3.旋转后与另一图形重合
性质 1.两个图形是全等图形 1.两个图形是全等图形
2.对称轴是对应点连线的垂直平分线 2.对称中心到对应点的距离相等
3.对应线段或延长线相交,交点在对称轴上 3.对应点与对称中心在同一条直线上
二、学习新知
活动1:求出:B(-3,-2),C(3,-2),连接AC可以发现它们过O点, A点与C点是关于点O成中心对称的,进一步观察它们的坐标可以发现它们的坐标特点:
关于原点对称的点的坐标变换法则:横纵坐标变为原来的相反数.
活动2:(1)
旋转的角度 90° 180° 270° 360°
对应点的坐标 (y,-x) (-x,-y) (-y,x) (x,y)
(2)略
活动3:在上述实验中,不管通过做几次旋转都可以画出一朵花,设为n,则旋转的角度为.
三、课堂练习
1. 90°
2.12 cm2
3.60°
4.55°
5.39°
四、自我检测
1.C 解析:∵∠AOB=90°,∠B=30°,
∴∠A=60°.
又∵OA=OA',
∴△AOA'是等边三角形.
∴∠AOA'=60°,即旋转角α为60°.故选C.
2.(36,0) 解析:∵每三次变换为一个循环,∴三角形⑩的直角顶点的横坐标为12×3=36.
3.(1)(2,3);
(2)图形略,(0,-6);
(3)(-7,3)或(-5,-3)或(3,3).
同课章节目录
