数学高中人教A版必修3教案:1.2.3循环语句
文档属性
| 名称 | 数学高中人教A版必修3教案:1.2.3循环语句 |

|
|
| 格式 | zip | ||
| 文件大小 | 251.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 00:00:00 | ||
图片预览


文档简介
第一章 算法初步
1.2 基本算法语句
1.2.3 循环语句
学习目标
1.理解基本算法语句的意义.
2.掌握循环语句的基本用法.
3.理解算法步骤、程序框图和算法语句的关系,学会算法语句的写法.
合作学习
一、设计问题,创设情境
请同学们思考以下的问题:
1.期末考试后,我们要求出全班60名同学的数学成绩的总分,你采用什么方式进行计算?
2.某单位在1 000名职工中寻找年龄最小的人参加某项活动,你采用什么方法进行筛选?
同学们,今天我们开始学习循环语句.
二、信息交流,揭示规律
问题1:循环结构有几种形式?
问题2:循环语句的格式及功能是什么样的?
问题3:两种循环语句的相同点与不同点分别是什么?
问题4:在程序中的循环语句与程序框图中的条件结构存在一一对应的关系吗?如何体现?
三、运用规律,解决问题
【例1】 修改前面编写过的求函数y=x3+3x2-24x+30的值的程序,连续输入自变量的11个取值,输出相应的函数值.
【例2】 教材中的用“二分法”求方程x2-2=0(x>0)的近似解的程序框图(如图),包含了顺序结构、条件结构和循环结构.如何把这个程序框图转化为相应的程序?
/
【例3】 设计一个计算1×3×5×7×…×99的解法,编写算法程序.
四、变式训练,深化提高
1.设计算法求
1
1×2
+
1
2×3
+
1
3×4
+…+
1
99×100
的值.要求画出程序框图,写出用基本语句编写的程序.
2.青年歌手电视大赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最低分后再求平均分.试设计一个算法解决该问题,要求画出程序框图,写出程序(假定分数采用10分制,即每位选手的最高分为10分,最低分为0分).
五、反思小结,观点提炼
1.循环语句有几种形式?格式是什么样的?
2.用两种循环语句编写计算机程序时应注意什么?
布置作业
课本P33习题1.2 A组第3题.
参考答案
二、信息交流,揭示规律
问题1:循环结构有两种形式:当型和直到型循环语句结构.
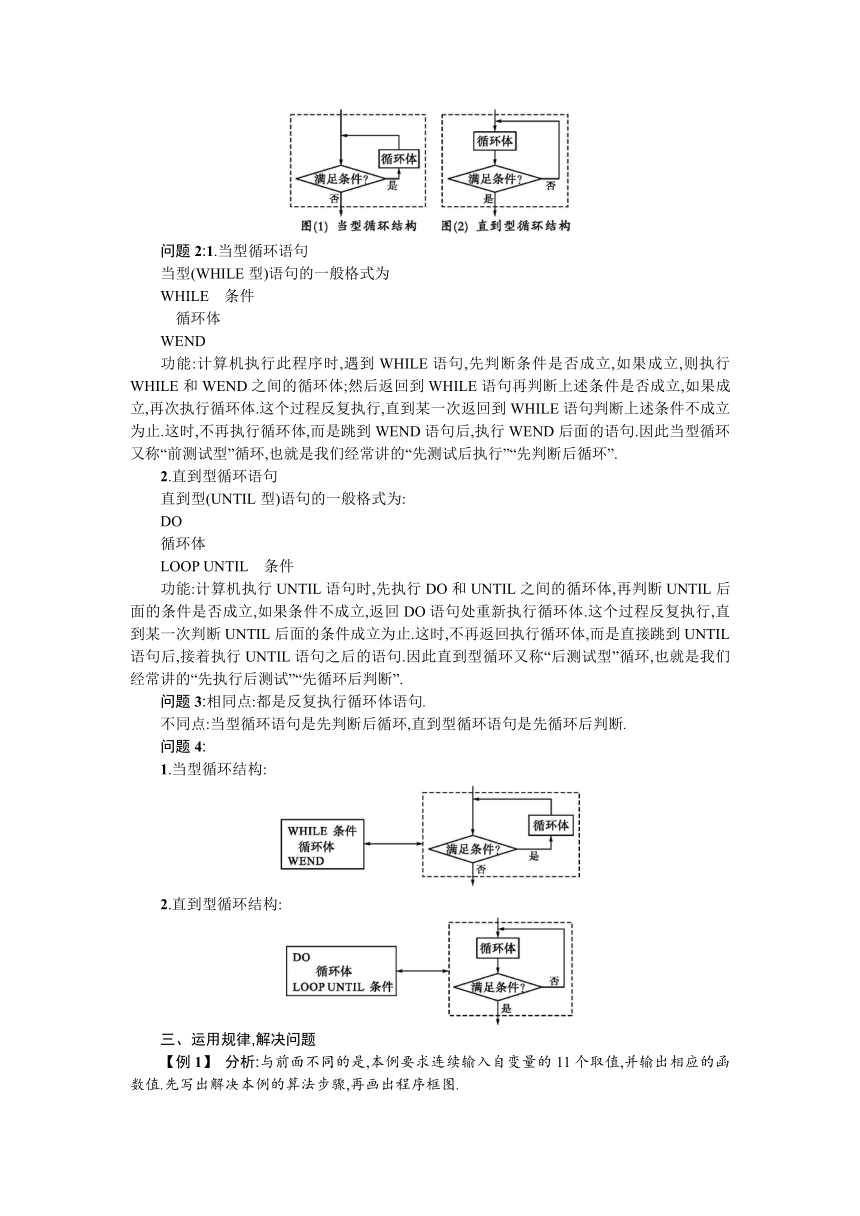
1.当型循环结构,如图(1)所示.
2.直到型循环结构,如图(2)所示.
/
问题2:1.当型循环语句
当型(WHILE型)语句的一般格式为
WHILE 条件
循环体
WEND
功能:计算机执行此程序时,遇到WHILE语句,先判断条件是否成立,如果成立,则执行WHILE和WEND之间的循环体;然后返回到WHILE语句再判断上述条件是否成立,如果成立,再次执行循环体.这个过程反复执行,直到某一次返回到WHILE语句判断上述条件不成立为止.这时,不再执行循环体,而是跳到WEND语句后,执行WEND后面的语句.因此当型循环又称“前测试型”循环,也就是我们经常讲的“先测试后执行”“先判断后循环”.
2.直到型循环语句
直到型(UNTIL型)语句的一般格式为:
DO
循环体
LOOP UNTIL 条件
功能:计算机执行UNTIL语句时,先执行DO和UNTIL之间的循环体,再判断UNTIL后面的条件是否成立,如果条件不成立,返回DO语句处重新执行循环体.这个过程反复执行,直到某一次判断UNTIL后面的条件成立为止.这时,不再返回执行循环体,而是直接跳到UNTIL语句后,接着执行UNTIL语句之后的语句.因此直到型循环又称“后测试型”循环,也就是我们经常讲的“先执行后测试”“先循环后判断”.
问题3:相同点:都是反复执行循环体语句.
不同点:当型循环语句是先判断后循环,直到型循环语句是先循环后判断.
问题4:
1.当型循环结构:
/
2.直到型循环结构:
/
三、运用规律,解决问题
【例1】 分析:与前面不同的是,本例要求连续输入自变量的11个取值,并输出相应的函数值.先写出解决本例的算法步骤,再画出程序框图.
解:第一步,输入自变量x的值.
第二步,计算y=x3+3x2-24x+30.
第三步,输出y.
第四步,记录输入次数.
第五步,判断输入的次数是否大于11.若是,则结束算法;否则,返回第一步.
显然,可以用计数变量n(1≤n≤11)记录次数,通过循环结构来实现算法.
程序框图:
/
程序:
n=1
DO
INPUT x
y=x^3+3?? x^2-24?? x+30
PRINT y
n=n+1
LOOP UNTIL n>11
END
【例2】 解:程序:
INPUT “a,b,d=”;a,b,d
DO
m=(a+b)/2
g=a^2-2
f=m^2-2
IF g?? f<0 THEN
b=m
ELSE
a=m
END IF
LOOP UNTIL ABS(a-b)PRINT m
END
【例3】 解:算法如下:
第一步,s=1.
第二步,i=3.
第三步,s=s·i.
第四步,i=i+2.
第五步,如果i≤99,那么转到第三步.
第六步,输出s.
程序:(“WHILE型”循环语句)
s=1
i=3
WHILE i<=99
s=s?? i
i=i+2
WEND
PRINT s
END
四、变式训练,深化提高
1.解:这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下:
/
程序如下:
s=0
i=1
DO
s=s+1/(i?? (i+1))
i=i+1
LOOP UNTIL i>99
PRINT s
END
2.解:由于共有12位评委,所以每位选手会有12个分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和.本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间,我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数.循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均分.
程序框图如下:
/
程序如下:
s=0
i=1
max=0
min=10
DO
INPUT x
s=s+x
IF max<=x THEN
max=x
END IF
IF min>=x THEN
min=x
END IF
i=i+1
LOOP UNTIL i>12
s1=s-max-min
a=s1/10
PRINT a
END
五、反思小结,观点提炼
1.两种形式,
(1)当型循环语句
当型(WHILE型)语句的一般格式为
WHILE 条件
循环体
WEND
(2)直到型循环语句
直到型(UNTIL型)语句的一般格式为
DO
循环体
LOOP UNTIL 条件
2.两种形式条件判断的先后顺序,即先判断条件还是先执行循环体.
1.2 基本算法语句
1.2.3 循环语句
学习目标
1.理解基本算法语句的意义.
2.掌握循环语句的基本用法.
3.理解算法步骤、程序框图和算法语句的关系,学会算法语句的写法.
合作学习
一、设计问题,创设情境
请同学们思考以下的问题:
1.期末考试后,我们要求出全班60名同学的数学成绩的总分,你采用什么方式进行计算?
2.某单位在1 000名职工中寻找年龄最小的人参加某项活动,你采用什么方法进行筛选?
同学们,今天我们开始学习循环语句.
二、信息交流,揭示规律
问题1:循环结构有几种形式?
问题2:循环语句的格式及功能是什么样的?
问题3:两种循环语句的相同点与不同点分别是什么?
问题4:在程序中的循环语句与程序框图中的条件结构存在一一对应的关系吗?如何体现?
三、运用规律,解决问题
【例1】 修改前面编写过的求函数y=x3+3x2-24x+30的值的程序,连续输入自变量的11个取值,输出相应的函数值.
【例2】 教材中的用“二分法”求方程x2-2=0(x>0)的近似解的程序框图(如图),包含了顺序结构、条件结构和循环结构.如何把这个程序框图转化为相应的程序?
/
【例3】 设计一个计算1×3×5×7×…×99的解法,编写算法程序.
四、变式训练,深化提高
1.设计算法求
1
1×2
+
1
2×3
+
1
3×4
+…+
1
99×100
的值.要求画出程序框图,写出用基本语句编写的程序.
2.青年歌手电视大赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最低分后再求平均分.试设计一个算法解决该问题,要求画出程序框图,写出程序(假定分数采用10分制,即每位选手的最高分为10分,最低分为0分).
五、反思小结,观点提炼
1.循环语句有几种形式?格式是什么样的?
2.用两种循环语句编写计算机程序时应注意什么?
布置作业
课本P33习题1.2 A组第3题.
参考答案
二、信息交流,揭示规律
问题1:循环结构有两种形式:当型和直到型循环语句结构.
1.当型循环结构,如图(1)所示.
2.直到型循环结构,如图(2)所示.
/
问题2:1.当型循环语句
当型(WHILE型)语句的一般格式为
WHILE 条件
循环体
WEND
功能:计算机执行此程序时,遇到WHILE语句,先判断条件是否成立,如果成立,则执行WHILE和WEND之间的循环体;然后返回到WHILE语句再判断上述条件是否成立,如果成立,再次执行循环体.这个过程反复执行,直到某一次返回到WHILE语句判断上述条件不成立为止.这时,不再执行循环体,而是跳到WEND语句后,执行WEND后面的语句.因此当型循环又称“前测试型”循环,也就是我们经常讲的“先测试后执行”“先判断后循环”.
2.直到型循环语句
直到型(UNTIL型)语句的一般格式为:
DO
循环体
LOOP UNTIL 条件
功能:计算机执行UNTIL语句时,先执行DO和UNTIL之间的循环体,再判断UNTIL后面的条件是否成立,如果条件不成立,返回DO语句处重新执行循环体.这个过程反复执行,直到某一次判断UNTIL后面的条件成立为止.这时,不再返回执行循环体,而是直接跳到UNTIL语句后,接着执行UNTIL语句之后的语句.因此直到型循环又称“后测试型”循环,也就是我们经常讲的“先执行后测试”“先循环后判断”.
问题3:相同点:都是反复执行循环体语句.
不同点:当型循环语句是先判断后循环,直到型循环语句是先循环后判断.
问题4:
1.当型循环结构:
/
2.直到型循环结构:
/
三、运用规律,解决问题
【例1】 分析:与前面不同的是,本例要求连续输入自变量的11个取值,并输出相应的函数值.先写出解决本例的算法步骤,再画出程序框图.
解:第一步,输入自变量x的值.
第二步,计算y=x3+3x2-24x+30.
第三步,输出y.
第四步,记录输入次数.
第五步,判断输入的次数是否大于11.若是,则结束算法;否则,返回第一步.
显然,可以用计数变量n(1≤n≤11)记录次数,通过循环结构来实现算法.
程序框图:
/
程序:
n=1
DO
INPUT x
y=x^3+3?? x^2-24?? x+30
PRINT y
n=n+1
LOOP UNTIL n>11
END
【例2】 解:程序:
INPUT “a,b,d=”;a,b,d
DO
m=(a+b)/2
g=a^2-2
f=m^2-2
IF g?? f<0 THEN
b=m
ELSE
a=m
END IF
LOOP UNTIL ABS(a-b)
END
【例3】 解:算法如下:
第一步,s=1.
第二步,i=3.
第三步,s=s·i.
第四步,i=i+2.
第五步,如果i≤99,那么转到第三步.
第六步,输出s.
程序:(“WHILE型”循环语句)
s=1
i=3
WHILE i<=99
s=s?? i
i=i+2
WEND
PRINT s
END
四、变式训练,深化提高
1.解:这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下:
/
程序如下:
s=0
i=1
DO
s=s+1/(i?? (i+1))
i=i+1
LOOP UNTIL i>99
PRINT s
END
2.解:由于共有12位评委,所以每位选手会有12个分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和.本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间,我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数.循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均分.
程序框图如下:
/
程序如下:
s=0
i=1
max=0
min=10
DO
INPUT x
s=s+x
IF max<=x THEN
max=x
END IF
IF min>=x THEN
min=x
END IF
i=i+1
LOOP UNTIL i>12
s1=s-max-min
a=s1/10
PRINT a
END
五、反思小结,观点提炼
1.两种形式,
(1)当型循环语句
当型(WHILE型)语句的一般格式为
WHILE 条件
循环体
WEND
(2)直到型循环语句
直到型(UNTIL型)语句的一般格式为
DO
循环体
LOOP UNTIL 条件
2.两种形式条件判断的先后顺序,即先判断条件还是先执行循环体.
