数学高中人教A版必修3教案:2.3.2两个变量的线性相关
文档属性
| 名称 | 数学高中人教A版必修3教案:2.3.2两个变量的线性相关 |

|
|
| 格式 | zip | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 00:00:00 | ||
图片预览



文档简介
第二章 统计
2.3 变量间的相关关系
2.3.2 两个变量的线性相关
学习目标
经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的回归方程的系数公式求回归方程.
合作学习
一、设计问题,创设情境
问题1:某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/℃
26
18
13
10
4
-1
杯数
20
24
34
38
50
64
如果某天的气温是-5 ℃,你能根据这些数据预测这天小卖部卖出热茶的杯数吗?
问题2:(1)正、负相关的概念是什么?
(2)什么是线性相关?
(3)看人体的脂肪百分比和年龄的散点图,当人的年龄增加时,体内脂肪含量到底是以什么方式增加的呢?
(4)什么叫做回归直线?
(5)如何求回归直线的方程?什么是最小二乘法?它有什么样的思想?
(6)利用计算机如何求回归直线的方程?
(7)利用计算器如何求回归直线的方程?
二、信息交流,揭示规律
问题2讨论结果
三、运用规律,解决问题
【例1】 有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/℃
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是2 ℃,预测这天卖出的热饮杯数.
【例2】 给出施化肥量对水稻产量影响的试验数据:
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
(1)画出上表的散点图;
(2)求出回归方程.
四、变式训练,深化提高
下表为某地近几年机动车辆数与交通事故数的统计资料:
机动车辆数x/千台
95
110
112
120
129
135
150
180
交通事故数y/千件
6.2
7.5
7.7
8.5
8.7
9.8
10.2
13
(1)请判断机动车辆数与交通事故数之间是否有线性相关关系,如果不具有线性相关关系,说明理由;
(2)如果具有线性相关关系,求出回归方程.
五、反思小结,观点提炼
请同学们想一想,求线性回归方程的步骤是什么?在里面有什么重要的方法?
布置作业
课本P94习题2.3 A组第3题.
课后巩固:
1.下列两个变量之间的关系不是函数关系的是( )
A.角度和它的余弦值 B.正方形边长和面积
C.正n边形的边数和它的内角和 D.人的年龄和身高
2.三点(3,10),(7,20),(11,24)的线性回归方程是( )
A.
y
^
=5.75-1.75x B.
y
^
=1.75+5.75x
C.
y
^
=1.75-5.75x D.
y
^
=5.75+1.75x
3.已知关于某设备的使用年限x与所支出的维修费用y(万元),有如下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
设y对x呈线性相关关系.试求:
(1)回归方程
y
^
=
b
^
x+
a
^
的回归系数
a
^
,
b
^
;
(2)估计使用年限为10年时,维修费用是多少?
4.我们考虑两个表示变量x与y之间的关系的模型,δ为误差项,模型如下:
模型1:y=6+4x;模型2:y=6+4x+δ.
(1)如果x=3,δ=1,分别求两个模型中y的值;
(2)分别说明以上两个模型是确定性模型还是随机性模型.
参考答案
二、信息交流,揭示规律
问题2讨论结果:(1)如果散点图中的点散布在从左下角到右上角的区域内,称为正相关.如果散点图中的点散布在从左上角到右下角的区域内,称为负相关.
(2)如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系.
(3)大体上来看,随着年龄的增加,人体中脂肪的百分比也在增加,呈正相关的趋势,我们可以从散点图上来进一步分析.
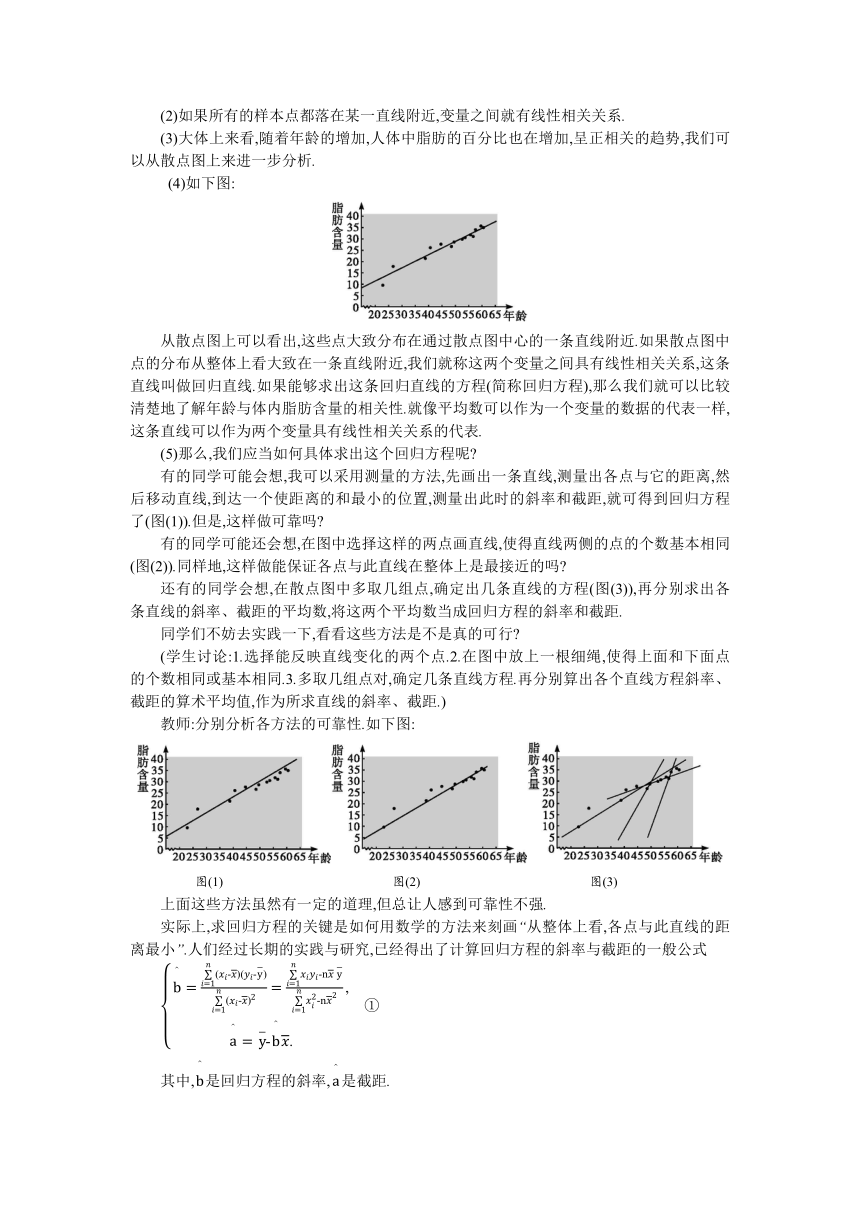
(4)如下图:
/
从散点图上可以看出,这些点大致分布在通过散点图中心的一条直线附近.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.就像平均数可以作为一个变量的数据的代表一样,这条直线可以作为两个变量具有线性相关关系的代表.
(5)那么,我们应当如何具体求出这个回归方程呢?
有的同学可能会想,我可以采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就可得到回归方程了(图(1)).但是,这样做可靠吗?
有的同学可能还会想,在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同(图(2)).同样地,这样做能保证各点与此直线在整体上是最接近的吗?
还有的同学会想,在散点图中多取几组点,确定出几条直线的方程(图(3)),再分别求出各条直线的斜率、截距的平均数,将这两个平均数当成回归方程的斜率和截距.
同学们不妨去实践一下,看看这些方法是不是真的可行?
(学生讨论:1.选择能反映直线变化的两个点.2.在图中放上一根细绳,使得上面和下面点的个数相同或基本相同.3.多取几组点对,确定几条直线方程.再分别算出各个直线方程斜率、截距的算术平均值,作为所求直线的斜率、截距.)
教师:分别分析各方法的可靠性.如下图:
///
图(1) 图(2) 图(3)
上面这些方法虽然有一定的道理,但总让人感到可靠性不强.
实际上,求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与此直线的距离最小”.人们经过长期的实践与研究,已经得出了计算回归方程的斜率与截距的一般公式
b
^
=
∑
??=1
??
(
??
??
-
??
)(
??
??
-
y
?
)
∑
??=1
??
(
??
??
-
??
)
2
=
∑
??=1
??
??
??
??
??
-n
??
y
?
∑
??=1
??
??
??
2
-n
??
2
,
a
^
=
y
?
-
b
^
??
.
①
其中,
b
^
是回归方程的斜率,
a
^
是截距.
推导公式①的计算比较复杂,这里不作推导.但是,我们可以解释一下得出它的原理.
假设我们已经得到两个具有线性相关关系的变量的一组数据
(x1,y1),(x2,y2),…,(xn,yn),
且所求回归方程是
y
^
=
b
^
x+
a
^
,
其中
a
^
,
b
^
是待定参数.当变量x取xi(i=1,2,…,n)时可以得到
y
^
=
b
^
xi+
a
^
(i=1,2,…,n),
/
它与实际收集到的yi之间的偏差是yi-
y
^
=yi-(
b
^
xi+
a
^
)(i=1,2,…,n).
这样,用这n个偏差的和来刻画“各点与此直线的整体偏差”是比较合适的.由于(yi-
y
^
)可正可负,为了避免相互抵消,可以考虑用
∑
??=1
??
|yi-
y
^
??
|来代替,但由于它含有绝对值,运算不太方便,所以改用Q=(y1-
b
^
x1-
a
^
)2+(y2-
b
^
x2-
a
^
)2+…+(yn-
b
^
xn-
a
^
)2 ②
来刻画n个点与回归直线在整体上的偏差.
这样,问题就归结为:当
a
^
,
b
^
取什么值时Q最小,即总体偏差最小.经过数学上求最小值的运算,
a
^
,
b
^
的值由公式①给出.
通过求②式的最小值而得到回归直线的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
(6)利用计算机求回归直线的方程.
根据最小二乘法的思想和公式①,利用计算器或计算机,可以方便地求出回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
①在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
②单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
③双击回归直线,弹出“趋势线格式”对话框.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程
y
^
=0.577x-0.448.
/
(7)利用计算器求回归直线的方程.
用计算器求这个回归方程的过程如下:
/
所以回归方程为
y
^
=0.577x-0.448.
正像本节开头所说的,我们从人体脂肪含量与年龄这两个变量的一组随机样本数据中,找到了它们之间关系的一个规律,这个规律是由回归直线来反映的.
回归方程的应用:
①描述两变量之间的依存关系;利用回归方程即可定量描述两个变量间依存的数量关系.
②利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间.
③利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标.如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度.
三、运用规律,解决问题
【例1】 解:(1)散点图如图所示:
/
(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.
(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式①求出回归方程的系数.
利用计算器容易求得回归方程
y
^
=-2.352x+147.767.
(4)当x=2时,
y
^
=143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.
【例2】 解:(1)散点图如下图:
/
(2)根据表中的数据进行具体计算,列成以下表格:
i
1
2
3
4
5
6
7
xi
15
20
25
30
35
40
45
yi
330
345
365
405
445
450
455
xiyi
4 950
6 900
9 125
12 150
15 575
18 000
20 475
x
=30,
y
?
=399.3,
∑
i=1
7
x
i
2
=7 000,
∑
i=1
7
y
i
2
=1 132 725,
∑
i=1
7
xiyi=87 175
故可得到
b
^
=
87 175-7×30×399.3
7 000-7×3
0
2
≈4.75,
a
^
=399.3-4.75×30≈257.
从而得回归方程是
y
^
=4.75x+257.
四、变式训练,深化提高
解:(1)在直角坐标系中画出数据的散点图,如下图:
/
直观判断散点在一条直线附近,故具有线性相关关系.
(2)计算相应的数据之和:
∑
??=1
8
xi=1 031,
∑
??=1
8
yi=71.6,
∑
??=1
8
??
??
2
=137 835,
∑
??=1
8
xiyi=9 611.7.
将它们代入公式计算得
b
^
≈0.077 4,
a
^
=-1.024 1,
所以,所求回归方程为
y
^
=0.077 4x-1.024 1.
五、反思小结,观点提炼
1.求线性回归方程的步骤:
(1)计算平均数
??
,
y
?
;
(2)计算xi与yi的积,求∑xiyi;
(3)计算∑
??
??
2
,
(4)将上述有关结果代入公式
b
^
=
∑
??=1
??
(
??
??
-
??
)(
??
??
-
y
?
)
∑
??=1
??
(
??
??
-
??
)
2
=
∑
??=1
??
??
??
??
??
-n
??
y
?
∑
??=1
??
??
??
2
-n
??
2
,
a
^
=
y
?
-
b
^
??
求
b
^
,
a
^
,写出回归方程.
2.经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的回归方程系数公式求回归方程.
课后巩固:
1.D 2.D
3.(1)
b
^
=1.23,
a
^
=0.08 (2)12.38万元
4.解:(1)模型1:y=6+4x=6+4×3=18;
模型2:y=6+4x+δ=6+4×3+1=19.
(2)模型1中相同的x值一定得到相同的y值,所以是确定性模型;模型2中相同的x值,因δ的不同,所得y值不一定相同,且δ是随机的,所以模型2是随机性模型.
2.3 变量间的相关关系
2.3.2 两个变量的线性相关
学习目标
经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的回归方程的系数公式求回归方程.
合作学习
一、设计问题,创设情境
问题1:某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/℃
26
18
13
10
4
-1
杯数
20
24
34
38
50
64
如果某天的气温是-5 ℃,你能根据这些数据预测这天小卖部卖出热茶的杯数吗?
问题2:(1)正、负相关的概念是什么?
(2)什么是线性相关?
(3)看人体的脂肪百分比和年龄的散点图,当人的年龄增加时,体内脂肪含量到底是以什么方式增加的呢?
(4)什么叫做回归直线?
(5)如何求回归直线的方程?什么是最小二乘法?它有什么样的思想?
(6)利用计算机如何求回归直线的方程?
(7)利用计算器如何求回归直线的方程?
二、信息交流,揭示规律
问题2讨论结果
三、运用规律,解决问题
【例1】 有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/℃
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是2 ℃,预测这天卖出的热饮杯数.
【例2】 给出施化肥量对水稻产量影响的试验数据:
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
(1)画出上表的散点图;
(2)求出回归方程.
四、变式训练,深化提高
下表为某地近几年机动车辆数与交通事故数的统计资料:
机动车辆数x/千台
95
110
112
120
129
135
150
180
交通事故数y/千件
6.2
7.5
7.7
8.5
8.7
9.8
10.2
13
(1)请判断机动车辆数与交通事故数之间是否有线性相关关系,如果不具有线性相关关系,说明理由;
(2)如果具有线性相关关系,求出回归方程.
五、反思小结,观点提炼
请同学们想一想,求线性回归方程的步骤是什么?在里面有什么重要的方法?
布置作业
课本P94习题2.3 A组第3题.
课后巩固:
1.下列两个变量之间的关系不是函数关系的是( )
A.角度和它的余弦值 B.正方形边长和面积
C.正n边形的边数和它的内角和 D.人的年龄和身高
2.三点(3,10),(7,20),(11,24)的线性回归方程是( )
A.
y
^
=5.75-1.75x B.
y
^
=1.75+5.75x
C.
y
^
=1.75-5.75x D.
y
^
=5.75+1.75x
3.已知关于某设备的使用年限x与所支出的维修费用y(万元),有如下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
设y对x呈线性相关关系.试求:
(1)回归方程
y
^
=
b
^
x+
a
^
的回归系数
a
^
,
b
^
;
(2)估计使用年限为10年时,维修费用是多少?
4.我们考虑两个表示变量x与y之间的关系的模型,δ为误差项,模型如下:
模型1:y=6+4x;模型2:y=6+4x+δ.
(1)如果x=3,δ=1,分别求两个模型中y的值;
(2)分别说明以上两个模型是确定性模型还是随机性模型.
参考答案
二、信息交流,揭示规律
问题2讨论结果:(1)如果散点图中的点散布在从左下角到右上角的区域内,称为正相关.如果散点图中的点散布在从左上角到右下角的区域内,称为负相关.
(2)如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系.
(3)大体上来看,随着年龄的增加,人体中脂肪的百分比也在增加,呈正相关的趋势,我们可以从散点图上来进一步分析.
(4)如下图:
/
从散点图上可以看出,这些点大致分布在通过散点图中心的一条直线附近.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.就像平均数可以作为一个变量的数据的代表一样,这条直线可以作为两个变量具有线性相关关系的代表.
(5)那么,我们应当如何具体求出这个回归方程呢?
有的同学可能会想,我可以采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就可得到回归方程了(图(1)).但是,这样做可靠吗?
有的同学可能还会想,在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同(图(2)).同样地,这样做能保证各点与此直线在整体上是最接近的吗?
还有的同学会想,在散点图中多取几组点,确定出几条直线的方程(图(3)),再分别求出各条直线的斜率、截距的平均数,将这两个平均数当成回归方程的斜率和截距.
同学们不妨去实践一下,看看这些方法是不是真的可行?
(学生讨论:1.选择能反映直线变化的两个点.2.在图中放上一根细绳,使得上面和下面点的个数相同或基本相同.3.多取几组点对,确定几条直线方程.再分别算出各个直线方程斜率、截距的算术平均值,作为所求直线的斜率、截距.)
教师:分别分析各方法的可靠性.如下图:
///
图(1) 图(2) 图(3)
上面这些方法虽然有一定的道理,但总让人感到可靠性不强.
实际上,求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与此直线的距离最小”.人们经过长期的实践与研究,已经得出了计算回归方程的斜率与截距的一般公式
b
^
=
∑
??=1
??
(
??
??
-
??
)(
??
??
-
y
?
)
∑
??=1
??
(
??
??
-
??
)
2
=
∑
??=1
??
??
??
??
??
-n
??
y
?
∑
??=1
??
??
??
2
-n
??
2
,
a
^
=
y
?
-
b
^
??
.
①
其中,
b
^
是回归方程的斜率,
a
^
是截距.
推导公式①的计算比较复杂,这里不作推导.但是,我们可以解释一下得出它的原理.
假设我们已经得到两个具有线性相关关系的变量的一组数据
(x1,y1),(x2,y2),…,(xn,yn),
且所求回归方程是
y
^
=
b
^
x+
a
^
,
其中
a
^
,
b
^
是待定参数.当变量x取xi(i=1,2,…,n)时可以得到
y
^
=
b
^
xi+
a
^
(i=1,2,…,n),
/
它与实际收集到的yi之间的偏差是yi-
y
^
=yi-(
b
^
xi+
a
^
)(i=1,2,…,n).
这样,用这n个偏差的和来刻画“各点与此直线的整体偏差”是比较合适的.由于(yi-
y
^
)可正可负,为了避免相互抵消,可以考虑用
∑
??=1
??
|yi-
y
^
??
|来代替,但由于它含有绝对值,运算不太方便,所以改用Q=(y1-
b
^
x1-
a
^
)2+(y2-
b
^
x2-
a
^
)2+…+(yn-
b
^
xn-
a
^
)2 ②
来刻画n个点与回归直线在整体上的偏差.
这样,问题就归结为:当
a
^
,
b
^
取什么值时Q最小,即总体偏差最小.经过数学上求最小值的运算,
a
^
,
b
^
的值由公式①给出.
通过求②式的最小值而得到回归直线的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
(6)利用计算机求回归直线的方程.
根据最小二乘法的思想和公式①,利用计算器或计算机,可以方便地求出回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
①在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
②单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
③双击回归直线,弹出“趋势线格式”对话框.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程
y
^
=0.577x-0.448.
/
(7)利用计算器求回归直线的方程.
用计算器求这个回归方程的过程如下:
/
所以回归方程为
y
^
=0.577x-0.448.
正像本节开头所说的,我们从人体脂肪含量与年龄这两个变量的一组随机样本数据中,找到了它们之间关系的一个规律,这个规律是由回归直线来反映的.
回归方程的应用:
①描述两变量之间的依存关系;利用回归方程即可定量描述两个变量间依存的数量关系.
②利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间.
③利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标.如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度.
三、运用规律,解决问题
【例1】 解:(1)散点图如图所示:
/
(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.
(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式①求出回归方程的系数.
利用计算器容易求得回归方程
y
^
=-2.352x+147.767.
(4)当x=2时,
y
^
=143.063.因此,某天的气温为2 ℃时,这天大约可以卖出143杯热饮.
【例2】 解:(1)散点图如下图:
/
(2)根据表中的数据进行具体计算,列成以下表格:
i
1
2
3
4
5
6
7
xi
15
20
25
30
35
40
45
yi
330
345
365
405
445
450
455
xiyi
4 950
6 900
9 125
12 150
15 575
18 000
20 475
x
=30,
y
?
=399.3,
∑
i=1
7
x
i
2
=7 000,
∑
i=1
7
y
i
2
=1 132 725,
∑
i=1
7
xiyi=87 175
故可得到
b
^
=
87 175-7×30×399.3
7 000-7×3
0
2
≈4.75,
a
^
=399.3-4.75×30≈257.
从而得回归方程是
y
^
=4.75x+257.
四、变式训练,深化提高
解:(1)在直角坐标系中画出数据的散点图,如下图:
/
直观判断散点在一条直线附近,故具有线性相关关系.
(2)计算相应的数据之和:
∑
??=1
8
xi=1 031,
∑
??=1
8
yi=71.6,
∑
??=1
8
??
??
2
=137 835,
∑
??=1
8
xiyi=9 611.7.
将它们代入公式计算得
b
^
≈0.077 4,
a
^
=-1.024 1,
所以,所求回归方程为
y
^
=0.077 4x-1.024 1.
五、反思小结,观点提炼
1.求线性回归方程的步骤:
(1)计算平均数
??
,
y
?
;
(2)计算xi与yi的积,求∑xiyi;
(3)计算∑
??
??
2
,
(4)将上述有关结果代入公式
b
^
=
∑
??=1
??
(
??
??
-
??
)(
??
??
-
y
?
)
∑
??=1
??
(
??
??
-
??
)
2
=
∑
??=1
??
??
??
??
??
-n
??
y
?
∑
??=1
??
??
??
2
-n
??
2
,
a
^
=
y
?
-
b
^
??
求
b
^
,
a
^
,写出回归方程.
2.经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的回归方程系数公式求回归方程.
课后巩固:
1.D 2.D
3.(1)
b
^
=1.23,
a
^
=0.08 (2)12.38万元
4.解:(1)模型1:y=6+4x=6+4×3=18;
模型2:y=6+4x+δ=6+4×3+1=19.
(2)模型1中相同的x值一定得到相同的y值,所以是确定性模型;模型2中相同的x值,因δ的不同,所得y值不一定相同,且δ是随机的,所以模型2是随机性模型.
