北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第11讲《一元一次不等式与不等式组》全章复习与巩固(提高)含答案
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第11讲《一元一次不等式与不等式组》全章复习与巩固(提高)含答案 | 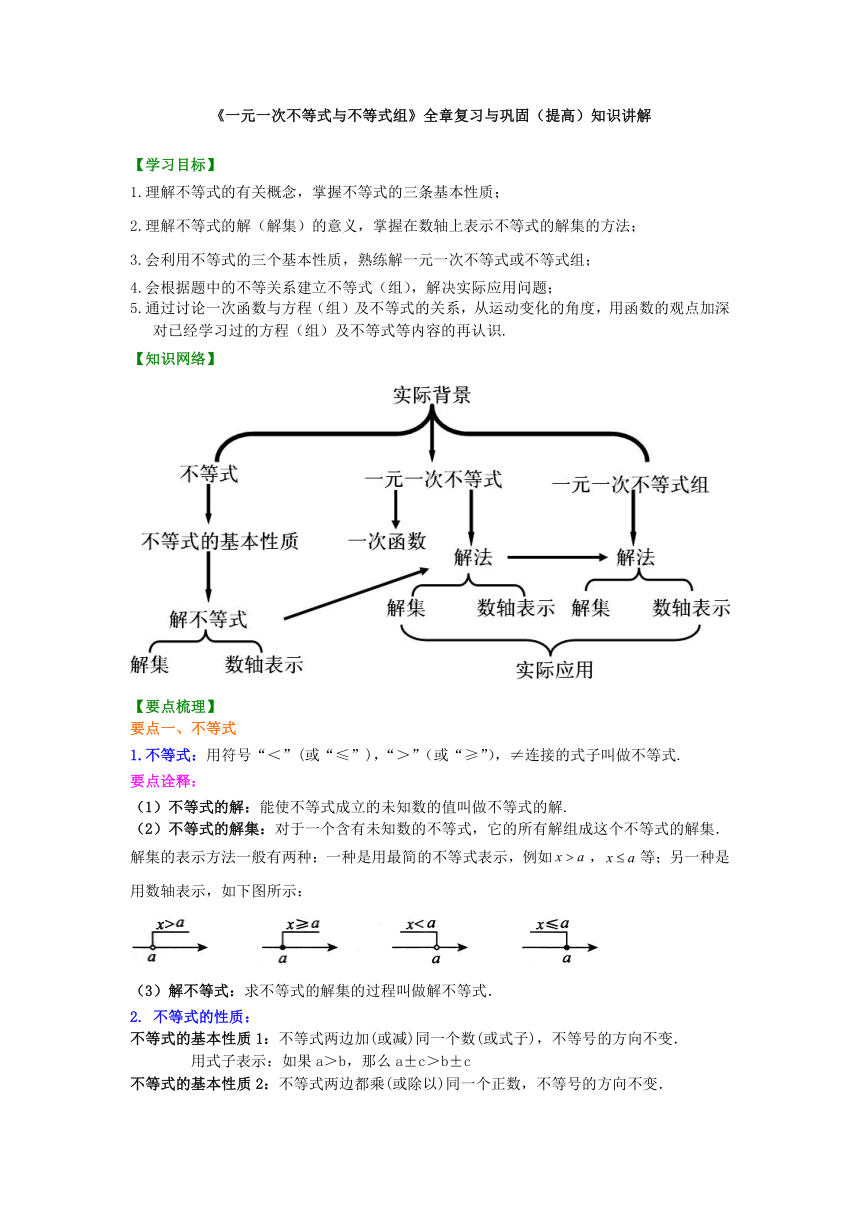 | |
| 格式 | zip | ||
| 文件大小 | 255.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-15 21:30:56 | ||
图片预览





文档简介
《一元一次不等式与不等式组》全章复习与巩固(提高)知识讲解
【学习目标】
1.理解不等式的有关概念,掌握不等式的三条基本性质;
2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;
3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组;
4.会根据题中的不等关系建立不等式(组),解决实际应用问题;
5.通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识.
【知识网络】
/
【要点梳理】
要点一、不等式
1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.
要点诠释:
(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.
(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.
解集的表示方法一般有两种:一种是用最简的不等式表示,例如/,/等;另一种是用数轴表示,如下图所示:
/
(3)解不等式:求不等式的解集的过程叫做解不等式.
2. 不等式的性质:
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
用式子表示:如果a>b,那么a±c>b±c
不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
用式子表示:如果a>b,c>0,那么ac>bc(或/).
不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
用式子表示:如果a>b,c<0,那么ac<bc(或/).
要点二、一元一次不等式
1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式.
要点诠释:ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.
2.解法:
解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 要点诠释:不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.
3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:
(1)审:认真审题,分清已知量、未知量;
(2)设:设出适当的未知数;
(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;
(4)列:根据题中的不等关系,列出不等式;
(5)解:解出所列的不等式的解集;
(6)答:检验是否符合题意,写出答案.
要点诠释:
列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.
要点三、一元一次不等式组 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 要点诠释:
(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.
(2)解不等式组:求不等式组解集的过程,叫做解不等式组.?
(3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集.?
(4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.
要点四、一次函数与一元一次方程、一元一次不等式(组)
方程(组)、不等式问题
函 数 问 题
从“数”的角度看
从“形”的角度看
求关于/、/的一元一次方程/=0(/≠0)的解
/为何值时,函数/的值为0?
确定直线/与/轴(即直线/=0)交点的横坐标.
求关于/、/的二元一次方程组/的解.
/为何值时,函数/与函数/的值相等?
确定直线/与直线/的交点的坐标.
求关于/的一元一次不等式/>0(/≠0)的解集
/为何值时,函数/的值大于0?
确定直线/在/轴(即直线/=0)上方部分的所有点的横坐标的范围.
【典型例题】
类型一、不等式
/1.用适当的语言翻译下列小题:
(1)x与9的差是正数或0;
(2)b与-5的和既不是正数也不是负数;
(3)y的5倍既大于x又小于3x+2;
(4)a的2倍与-4的差小于5或大于7;
(5)/;
(6)/;
(7)/
(8)/
【答案与解析】
解:(1)x -9≥0;
(2)b+(-5)=0;
(3)x<5y<3x+2;
(4)2a-(-4)<5或2a-(-4)>7;
(5)y的一半与x的差非负;
(6)x的一半与3的差既大于-2又小于0;
(7)x>-3或写作:大于-3的数;
(8)2【总结升华】对“既……又……”,“既是……也是……”,“是……或是……”等连接词也要逐步领会积累.
/2. 设x>y,试比较代数式-(8-10x)与-(8-10y)的大小,如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
【思路点拨】比较两个代数式的大小,可以运用不等式的性质得出比较方法.
【答案与解析】
解:可利用作差比较法比较大小.
-(8-l0x)-[ -(8-l0y)]
=-8+10x+8-10y
=10x -10y.
∵x>y,∴10x>10y,∴10x -10y>0
∴-(8-l0x)>-(8-l0y).
按题意-(8-l0x)>0,则10x>8.
∴/.
∴x的最小正整数值是1.
【总结升华】两个数量的大小可以通过它们的差来判断:
①/;
②/;
③/.
举一反三:
【变式】己知:x<0.5,比较2-4x和18x-9的大小.
【答案】
解:∵2-4x-(18x-9)=11-22x
而又∵x<0.5,
∴-22x>-11,即11-22x>0.
∴2-4x>18x-9.
类型二、一元一次不等式 ?
/3. 已知关于x的不等式/的解集是/,求a的取值范围.
【答案与解析】
解:解法一:/,
/,
∵它的解集为/,
/, /.
解法二:/是关于x方程/ 的解,
/,解得/.
/.
【总结升华】不等式解集中的端点值就是对应方程的解.
举一反三:
【变式1】如果关于x的不等式/正整数解为1、2、3, 则正整数k应取怎样的值?
【答案】解不等式得:/.
∵k为正整数且/中的正整数解为1,2,3,
∴/.
∴/.
【变式2】(2019?南通)关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围是( )
A.﹣3<b<﹣2 B.﹣3<b≤﹣2 C.﹣3≤b≤﹣2 D.﹣3≤b<﹣2
【答案】D.
解:由x﹣b>0解得:x>b,
∵不等式的负整数解只有两个负整数解,
∴﹣3≤b<﹣2.
类型三、一元一次不等式组
/4. 求不等式组/的整数解.
【思路点拨】分别解出各不等式,取所有解集的公共部分.
【答案与解析】
解:/
解不等式①得:x<2 .
解不等式②得:x≥-1 .
解不等式③得:x>-2 .
∴不等式组的解集为-1≤x<2 .
故不等式组的整数解为-1,0,1 .
【总结升华】求不等式组的特殊解的一般步骤是先求出不等式组的解集,再从中找出符合要求的特殊解.
举一反三:
【变式】若关于不等式组/只有四个整数解,求a的取值范围.
【答案】
解:由/,得/,
由/,得/,
∴不等式组的解集为/,
∵只有四个整数解,∴/,即/,
∴a的取值范围:/.
/5. 某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台.三种家电的进价和售价如下表所示:
价格
种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰 箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机的数量和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定:农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家财政最多需补贴农民多少元?
【思路点拨】 (1)设购进电视机、冰箱各x台,则洗衣机为(15-2x)台.根据两个关键词:“不大于”、“不超过”就可以建立不等式组,根据x的取值讨论确定进货方案.(2)分别求出(1)中各方案所需的补贴,再比较确定国家财政的最多补贴.
【答案与解析】
解:(1)设购进电视机、冰箱各x台.
依题意,得/
解这个不等式组得,6≤x≤7
∵ x为正整数.∴ x=6或7.
方案一:购进电视机和冰箱各6台,洗衣机3台;
方案二:购进电视机和冰箱各7台,洗衣机1台.
(2)方案1需补贴:
(6×2100+6×2500+3×1700)×13%=4251(元).
方案二需补贴:
(7×2100+7×2500+1×1700)×13%=4407(元).
∴ 国家财政最多需补贴农民4407元.
【总结升华】利用不等式解答实际问题的策略是:①根据题意构建不等式(组);解这个不等式(组);②由不等式(组)的整数解的个数确定方案.
类型四、一次函数与一元一次方程、不等式(组)
/6.如图,直线/经过A(-2,-1)和B(-3,0)两点,则不等式组/ 的解集为 .
/
【答案】/;
【解析】从图象上看,/的图象在/轴下方,且在/上方的图象为画红线的部分,而这部分的图象自变量/的范围在/.
/
【总结升华】也可以先求出/的解析式,然后解不等式得出结果.
举一反三:
【变式】如图所示,直线/经过点A(-1,-2)和点B(-2,0),直线/过点A,则不等式2/</<0的解集为( ) .
/
A./<-2 B.-2</<-1 C.-2</<0 D.-1</<0
【答案】B;
提示:由图象可知A(-1,-2)是直线/与直线/的交点,当/<-1时2/</,当/>-2时,/<0,所以-2</<-1是不等式2/</<0的解集.
类型五、综合应用
/7.已知不等式组/的解集为/,试求m,n的值.
【答案与解析】
解:解不等式/,得/.
解不等式 n-4(x-1)<1,得/.
因为不等式组的解集为/,
所以有/, ∴ /.
答:m、n的值分别1和3.
【总结升华】先分别求出每一个不等式的解集,再求出这个不等式组的解集,然后根据题意,建立关于m、n的方程求解.
/8.(2019?泸州)某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
【思路点拨】(1)设A种商品的单价为x元、B种商品的单价为y元,根据等量关系:①购买60件A商品的钱数+30件B商品的钱数=1080元,②购买50件A商品的钱数+20件B商品的钱数=880元分别列出方程,联立求解即可.
(2)设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,根据不等关系:①购买A、B两种商品的总件数不少于32件,②购买的A、B两种商品的总费用不超过296元可分别列出不等式,联立求解可得出m的取值范围,进而讨论各方案即可.
【答案与解析】
解:(1)设A种商品的单价为x元、B种商品的单价为y元,由题意得:
/,
解得/.
答:A种商品的单价为16元、B种商品的单价为4元.
(2)设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,由题意得:
/,
解得:12≤m≤13,
∵m是整数,
∴m=12或13,
故有如下两种方案:
方案(1):m=12,2m﹣4=20 即购买A商品的件数为12件,则购买B商品的件数为20件;
方案(2):m=13,2m﹣4=22 即购买A商品的件数为13件,则购买B商品的件数为22件.
【总结升华】此题考查了一元一次不等式组及二元一次方程组的应用,解答此类应用类题目的关键是仔细审题,得出等量关系,从而转化为方程或不等式解题,第二问需要分类讨论,注意不要遗漏.
举一反三:
【变式】某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.
(1)求甲、乙两种花木每株成本分别为多少元?
(2)据市场调研,1株甲种花木售价为760元, 1株乙种花木售价为540元.该花农决定在成本不超过30000元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?
【答案】
解:(1)设甲、乙两种花木的成本价分别为x元和y元.
由题意得:/, 解得:/ .
(2)设种植甲种花木为a株,则种植乙种花木为(3a+10)株.
则有:/
解得:/.
由于a为整数,∴a可取18或19或20,所以有三种具体方案:
①种植甲种花木18株,种植乙种花木3a+10=64株;
②种植甲种花木19株,种植乙种花木3a+10=67株;
③种植甲种花木20株,种植乙种花木3a+10=70株.
【巩固练习】
一、选择题
1.(2019?潍坊)不等式组/的所有整数解的和是( )
A.2 B.3 C.5 D.6
2.某商场的老板销售一种商品,他要以不低于进价20%价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价多少时商店老板才能出售( ).
A.80元 B.100元 C.120元 D.160元
3.已知一次函数/的图象过第一、二、四象限,且与/轴交于点(2,0),则关于/的不等式/的解集为( ).
A./<-1 B./> -1 C. />1 D./<1
4.若不等式组/ 有解,则/的取值范围是( ).
A./ B. / C./ D. /
5.如果不等式ax+4<0的解集在数轴上表示如图,那么a的值是( ) .
A.a >0 B.a<0 C.a=-2 D.a=2
/
6. 中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与两个球体质量相等的正方体的个数为( ) .
A.5 B.4 C.3 D.2
/
7.如果一次函数当自变量/的取值范围是/时,函数值/的取值范围是/,那么此函数的解析式是( ) .
A./ B./
C./或/ D./或/
8.(2019?老河口市模拟)已知关于x的不等式组/有且只有1个整数解,则a的取值范围是( )
A.a>1 B.1≤a<2 C.1<a≤2 D.a≤2
二、填空题
9.(2019?江都市模拟)如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是 .
10.已知方程组/的解满足/,则a的取值范围 .
11. 若不等式组/无解,则/的取值范围是 .
12. 如图,直线/经过A(2,1),B(-1,-2)两点,则不等式/的解集为__________.
/
13.已知关于x的方程3k-5x=-9的解是非负数,求k的取值范围 .
14.如果关于/的不等式组/的整数解仅为1,2,3,则/的取值范围是 ,/的取值范围是 .
15. 为确保信息安全,信息需加密传输,发送方将明加密为密文传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为:明文a,b对应的密文为a-2b,2a+b.例如,明文1,2对应的密文是-3,4,当接收方收到密文是1,7时,解密得到的明文是 .
16.若不等式组:
/只有一个整数解,则a的取值范围 .
三、解答题
17.(2019?甘南州)解不等式组:/,并把解集在数轴上表示出来.
18.(2019?呼和浩特)已知关于x的不等式组/有四个整数解,求实数a的取值范围.
19.某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
20. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药2/后血液中的含药量最高,达每升6/,接着逐步衰减,10/后血液中的含药量为每升3/,每升血液中的含药量//随时间//的变化情况如图所示.当成人按规定剂量服药后:
/
(1)分别求出/≤2和/≥2时,/与/之间的函数关系式;
(2)如果每升血液中的含药量为4/或4/以上时,治疗疾病是有效的,那么这个有效时间是多长?
【答案与解析】
一.选择题
1.【答案】D.
【解析】/∵解不等式①得;x>﹣/,解不等式②得;x≤3,
∴不等式组的解集为﹣/<x≤3,∴不等式组的整数解为0,1,2,3,0+1+2+3=6.
2. 【答案】C;
【解析】解:设降价x元时商店老板才能出售.则可得: 360-x≥/×(1+20%),
解得:x≤120.
3. 【答案】A;
【解析】一次函数/的图象过第一、二、四象限,所以/<0,将(2, 0)代入/,得/,所以/,所以/.
4. 【答案】A;
【解析】画数轴进行分析.
5. 【答案】C;
【解析】由已知a<0且x>-/,则-/,即/.
6. 【答案】A ;
【解析】设一个球体、圆柱体与正方体的质量分别为x、y、z, 根据已知条件,
有/
①×2-②×5,得2x=5y,即与2个球体质量相等的正方体的个数为5.
7. 【答案】C;
【解析】分/>0和/<0两种情况讨论.
8. 【答案】B;
【解析】解:解不等式x﹣a>0,得:x>a,
解不等式7﹣2x>1,得:x<3,
∵不等式组有且只有1个整数解,
∴不等式组的整数解为2,
∴1≤a<2,
故选:B.
二.填空题
9.【答案】a<﹣1.
10.【答案】/;
【解析】方程组/得:/, 所以/,
∴/解得:-/.
11. 【答案】/;
【解析】要使原不等式无解,则需满足/,得/≥2.
12. 【答案】-1</<2;
【解析】由于直线/经过A(2,1),B(-1,-2)两点,那么把A、B两点的坐标代入/,用待定系数法求出/、/的值,然后解不等式组/,即可求出解集.
13.【答案】 k≥-3;
【解析】3k-5x=-9,x=/,/ 解得k≥-3.
14. 【答案】/,/;
15.【答案】3,1;
【解析】由于本密码的解密钥匙是: 明文a,b对应的密文为a-2b,2a+b.
故当密文是1,7时,
得/, 解得/.
也就是说,密文1,7分别对应明文3,1.
16.【答案】1<a≤2.
【解析】先把a看成一个固定数,解关于x的不等式组,再由不等式组的解集研究a的取值范围.
三.解答题
17.【解析】
解:/,
由不等式①移项得:4x+x>1﹣6,
整理得:5x>﹣5,
解得:x>﹣1,…(1分)
由不等式②去括号得:3x﹣3≤x+5,
移项得:3x﹣x≤5+3,
合并得:2x≤8,
解得:x≤4,
则不等式组的解集为﹣1<x≤4.
在数轴上表示不等式组的解集如图所示,
/
18.【解析】
解:解不等式组/,
解不等式①得:x>﹣/,
解不等式②得:x≤a+4,
∵不等式组有四个整数解,
∴1≤a+4<2,
解得:﹣3≤a<﹣2.
19.【解析】
解:(1)设新建1个地上停车位需要x万元,新建1个地下停车位需y万元,
根据题意,得/, 解得:/
答:新建1个地上停车位需要0.1万元,新建1个地下停车位需0.5万元. (2)设建m个地上停车位,则建(50-m)个地下停车位,根据题意,得
12<0.1m+0.5(50-m)≤13, 解得:30≤m</ ∵m为整数, ∴m=30,31,32
∴50-m=20,19,18.
答:有三种建造方案:方案一:新建30个地上停车位和20个地下停车位;方案二:新建31个地上停车位和19个地下停车位;方案三:新建32个地上停车位和18个地下停车位.
20. 【解析】
解:(1)由图知,/≤2时是正比例函数,/≥2时是一次函数.
设/≤2时,/,把(2,6)代入/,解得/=3,
∴ 当0≤/≤2时,/.
设/≥2时,/,把(2,6),(10,3)代入/中,
得/,解得/,即/.
当/=0时,有/,/.
∴ 当2≤/≤18时,/.
(2)由于/≥4时在治疗疾病是有效的,
∴ /,解得/.
即服药后/得到/为治病的有效时间,
这段时间为/.
【学习目标】
1.理解不等式的有关概念,掌握不等式的三条基本性质;
2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;
3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组;
4.会根据题中的不等关系建立不等式(组),解决实际应用问题;
5.通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识.
【知识网络】
/
【要点梳理】
要点一、不等式
1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.
要点诠释:
(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.
(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.
解集的表示方法一般有两种:一种是用最简的不等式表示,例如/,/等;另一种是用数轴表示,如下图所示:
/
(3)解不等式:求不等式的解集的过程叫做解不等式.
2. 不等式的性质:
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
用式子表示:如果a>b,那么a±c>b±c
不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
用式子表示:如果a>b,c>0,那么ac>bc(或/).
不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
用式子表示:如果a>b,c<0,那么ac<bc(或/).
要点二、一元一次不等式
1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式.
要点诠释:ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.
2.解法:
解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 要点诠释:不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.
3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:
(1)审:认真审题,分清已知量、未知量;
(2)设:设出适当的未知数;
(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;
(4)列:根据题中的不等关系,列出不等式;
(5)解:解出所列的不等式的解集;
(6)答:检验是否符合题意,写出答案.
要点诠释:
列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.
要点三、一元一次不等式组 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 要点诠释:
(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.
(2)解不等式组:求不等式组解集的过程,叫做解不等式组.?
(3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集.?
(4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.
要点四、一次函数与一元一次方程、一元一次不等式(组)
方程(组)、不等式问题
函 数 问 题
从“数”的角度看
从“形”的角度看
求关于/、/的一元一次方程/=0(/≠0)的解
/为何值时,函数/的值为0?
确定直线/与/轴(即直线/=0)交点的横坐标.
求关于/、/的二元一次方程组/的解.
/为何值时,函数/与函数/的值相等?
确定直线/与直线/的交点的坐标.
求关于/的一元一次不等式/>0(/≠0)的解集
/为何值时,函数/的值大于0?
确定直线/在/轴(即直线/=0)上方部分的所有点的横坐标的范围.
【典型例题】
类型一、不等式
/1.用适当的语言翻译下列小题:
(1)x与9的差是正数或0;
(2)b与-5的和既不是正数也不是负数;
(3)y的5倍既大于x又小于3x+2;
(4)a的2倍与-4的差小于5或大于7;
(5)/;
(6)/;
(7)/
(8)/
【答案与解析】
解:(1)x -9≥0;
(2)b+(-5)=0;
(3)x<5y<3x+2;
(4)2a-(-4)<5或2a-(-4)>7;
(5)y的一半与x的差非负;
(6)x的一半与3的差既大于-2又小于0;
(7)x>-3或写作:大于-3的数;
(8)2
/2. 设x>y,试比较代数式-(8-10x)与-(8-10y)的大小,如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
【思路点拨】比较两个代数式的大小,可以运用不等式的性质得出比较方法.
【答案与解析】
解:可利用作差比较法比较大小.
-(8-l0x)-[ -(8-l0y)]
=-8+10x+8-10y
=10x -10y.
∵x>y,∴10x>10y,∴10x -10y>0
∴-(8-l0x)>-(8-l0y).
按题意-(8-l0x)>0,则10x>8.
∴/.
∴x的最小正整数值是1.
【总结升华】两个数量的大小可以通过它们的差来判断:
①/;
②/;
③/.
举一反三:
【变式】己知:x<0.5,比较2-4x和18x-9的大小.
【答案】
解:∵2-4x-(18x-9)=11-22x
而又∵x<0.5,
∴-22x>-11,即11-22x>0.
∴2-4x>18x-9.
类型二、一元一次不等式 ?
/3. 已知关于x的不等式/的解集是/,求a的取值范围.
【答案与解析】
解:解法一:/,
/,
∵它的解集为/,
/, /.
解法二:/是关于x方程/ 的解,
/,解得/.
/.
【总结升华】不等式解集中的端点值就是对应方程的解.
举一反三:
【变式1】如果关于x的不等式/正整数解为1、2、3, 则正整数k应取怎样的值?
【答案】解不等式得:/.
∵k为正整数且/中的正整数解为1,2,3,
∴/.
∴/.
【变式2】(2019?南通)关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围是( )
A.﹣3<b<﹣2 B.﹣3<b≤﹣2 C.﹣3≤b≤﹣2 D.﹣3≤b<﹣2
【答案】D.
解:由x﹣b>0解得:x>b,
∵不等式的负整数解只有两个负整数解,
∴﹣3≤b<﹣2.
类型三、一元一次不等式组
/4. 求不等式组/的整数解.
【思路点拨】分别解出各不等式,取所有解集的公共部分.
【答案与解析】
解:/
解不等式①得:x<2 .
解不等式②得:x≥-1 .
解不等式③得:x>-2 .
∴不等式组的解集为-1≤x<2 .
故不等式组的整数解为-1,0,1 .
【总结升华】求不等式组的特殊解的一般步骤是先求出不等式组的解集,再从中找出符合要求的特殊解.
举一反三:
【变式】若关于不等式组/只有四个整数解,求a的取值范围.
【答案】
解:由/,得/,
由/,得/,
∴不等式组的解集为/,
∵只有四个整数解,∴/,即/,
∴a的取值范围:/.
/5. 某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台.三种家电的进价和售价如下表所示:
价格
种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰 箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机的数量和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定:农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家财政最多需补贴农民多少元?
【思路点拨】 (1)设购进电视机、冰箱各x台,则洗衣机为(15-2x)台.根据两个关键词:“不大于”、“不超过”就可以建立不等式组,根据x的取值讨论确定进货方案.(2)分别求出(1)中各方案所需的补贴,再比较确定国家财政的最多补贴.
【答案与解析】
解:(1)设购进电视机、冰箱各x台.
依题意,得/
解这个不等式组得,6≤x≤7
∵ x为正整数.∴ x=6或7.
方案一:购进电视机和冰箱各6台,洗衣机3台;
方案二:购进电视机和冰箱各7台,洗衣机1台.
(2)方案1需补贴:
(6×2100+6×2500+3×1700)×13%=4251(元).
方案二需补贴:
(7×2100+7×2500+1×1700)×13%=4407(元).
∴ 国家财政最多需补贴农民4407元.
【总结升华】利用不等式解答实际问题的策略是:①根据题意构建不等式(组);解这个不等式(组);②由不等式(组)的整数解的个数确定方案.
类型四、一次函数与一元一次方程、不等式(组)
/6.如图,直线/经过A(-2,-1)和B(-3,0)两点,则不等式组/ 的解集为 .
/
【答案】/;
【解析】从图象上看,/的图象在/轴下方,且在/上方的图象为画红线的部分,而这部分的图象自变量/的范围在/.
/
【总结升华】也可以先求出/的解析式,然后解不等式得出结果.
举一反三:
【变式】如图所示,直线/经过点A(-1,-2)和点B(-2,0),直线/过点A,则不等式2/</<0的解集为( ) .
/
A./<-2 B.-2</<-1 C.-2</<0 D.-1</<0
【答案】B;
提示:由图象可知A(-1,-2)是直线/与直线/的交点,当/<-1时2/</,当/>-2时,/<0,所以-2</<-1是不等式2/</<0的解集.
类型五、综合应用
/7.已知不等式组/的解集为/,试求m,n的值.
【答案与解析】
解:解不等式/,得/.
解不等式 n-4(x-1)<1,得/.
因为不等式组的解集为/,
所以有/, ∴ /.
答:m、n的值分别1和3.
【总结升华】先分别求出每一个不等式的解集,再求出这个不等式组的解集,然后根据题意,建立关于m、n的方程求解.
/8.(2019?泸州)某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
【思路点拨】(1)设A种商品的单价为x元、B种商品的单价为y元,根据等量关系:①购买60件A商品的钱数+30件B商品的钱数=1080元,②购买50件A商品的钱数+20件B商品的钱数=880元分别列出方程,联立求解即可.
(2)设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,根据不等关系:①购买A、B两种商品的总件数不少于32件,②购买的A、B两种商品的总费用不超过296元可分别列出不等式,联立求解可得出m的取值范围,进而讨论各方案即可.
【答案与解析】
解:(1)设A种商品的单价为x元、B种商品的单价为y元,由题意得:
/,
解得/.
答:A种商品的单价为16元、B种商品的单价为4元.
(2)设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,由题意得:
/,
解得:12≤m≤13,
∵m是整数,
∴m=12或13,
故有如下两种方案:
方案(1):m=12,2m﹣4=20 即购买A商品的件数为12件,则购买B商品的件数为20件;
方案(2):m=13,2m﹣4=22 即购买A商品的件数为13件,则购买B商品的件数为22件.
【总结升华】此题考查了一元一次不等式组及二元一次方程组的应用,解答此类应用类题目的关键是仔细审题,得出等量关系,从而转化为方程或不等式解题,第二问需要分类讨论,注意不要遗漏.
举一反三:
【变式】某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.
(1)求甲、乙两种花木每株成本分别为多少元?
(2)据市场调研,1株甲种花木售价为760元, 1株乙种花木售价为540元.该花农决定在成本不超过30000元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?
【答案】
解:(1)设甲、乙两种花木的成本价分别为x元和y元.
由题意得:/, 解得:/ .
(2)设种植甲种花木为a株,则种植乙种花木为(3a+10)株.
则有:/
解得:/.
由于a为整数,∴a可取18或19或20,所以有三种具体方案:
①种植甲种花木18株,种植乙种花木3a+10=64株;
②种植甲种花木19株,种植乙种花木3a+10=67株;
③种植甲种花木20株,种植乙种花木3a+10=70株.
【巩固练习】
一、选择题
1.(2019?潍坊)不等式组/的所有整数解的和是( )
A.2 B.3 C.5 D.6
2.某商场的老板销售一种商品,他要以不低于进价20%价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价多少时商店老板才能出售( ).
A.80元 B.100元 C.120元 D.160元
3.已知一次函数/的图象过第一、二、四象限,且与/轴交于点(2,0),则关于/的不等式/的解集为( ).
A./<-1 B./> -1 C. />1 D./<1
4.若不等式组/ 有解,则/的取值范围是( ).
A./ B. / C./ D. /
5.如果不等式ax+4<0的解集在数轴上表示如图,那么a的值是( ) .
A.a >0 B.a<0 C.a=-2 D.a=2
/
6. 中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与两个球体质量相等的正方体的个数为( ) .
A.5 B.4 C.3 D.2
/
7.如果一次函数当自变量/的取值范围是/时,函数值/的取值范围是/,那么此函数的解析式是( ) .
A./ B./
C./或/ D./或/
8.(2019?老河口市模拟)已知关于x的不等式组/有且只有1个整数解,则a的取值范围是( )
A.a>1 B.1≤a<2 C.1<a≤2 D.a≤2
二、填空题
9.(2019?江都市模拟)如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是 .
10.已知方程组/的解满足/,则a的取值范围 .
11. 若不等式组/无解,则/的取值范围是 .
12. 如图,直线/经过A(2,1),B(-1,-2)两点,则不等式/的解集为__________.
/
13.已知关于x的方程3k-5x=-9的解是非负数,求k的取值范围 .
14.如果关于/的不等式组/的整数解仅为1,2,3,则/的取值范围是 ,/的取值范围是 .
15. 为确保信息安全,信息需加密传输,发送方将明加密为密文传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为:明文a,b对应的密文为a-2b,2a+b.例如,明文1,2对应的密文是-3,4,当接收方收到密文是1,7时,解密得到的明文是 .
16.若不等式组:
/只有一个整数解,则a的取值范围 .
三、解答题
17.(2019?甘南州)解不等式组:/,并把解集在数轴上表示出来.
18.(2019?呼和浩特)已知关于x的不等式组/有四个整数解,求实数a的取值范围.
19.某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
20. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药2/后血液中的含药量最高,达每升6/,接着逐步衰减,10/后血液中的含药量为每升3/,每升血液中的含药量//随时间//的变化情况如图所示.当成人按规定剂量服药后:
/
(1)分别求出/≤2和/≥2时,/与/之间的函数关系式;
(2)如果每升血液中的含药量为4/或4/以上时,治疗疾病是有效的,那么这个有效时间是多长?
【答案与解析】
一.选择题
1.【答案】D.
【解析】/∵解不等式①得;x>﹣/,解不等式②得;x≤3,
∴不等式组的解集为﹣/<x≤3,∴不等式组的整数解为0,1,2,3,0+1+2+3=6.
2. 【答案】C;
【解析】解:设降价x元时商店老板才能出售.则可得: 360-x≥/×(1+20%),
解得:x≤120.
3. 【答案】A;
【解析】一次函数/的图象过第一、二、四象限,所以/<0,将(2, 0)代入/,得/,所以/,所以/.
4. 【答案】A;
【解析】画数轴进行分析.
5. 【答案】C;
【解析】由已知a<0且x>-/,则-/,即/.
6. 【答案】A ;
【解析】设一个球体、圆柱体与正方体的质量分别为x、y、z, 根据已知条件,
有/
①×2-②×5,得2x=5y,即与2个球体质量相等的正方体的个数为5.
7. 【答案】C;
【解析】分/>0和/<0两种情况讨论.
8. 【答案】B;
【解析】解:解不等式x﹣a>0,得:x>a,
解不等式7﹣2x>1,得:x<3,
∵不等式组有且只有1个整数解,
∴不等式组的整数解为2,
∴1≤a<2,
故选:B.
二.填空题
9.【答案】a<﹣1.
10.【答案】/;
【解析】方程组/得:/, 所以/,
∴/解得:-/.
11. 【答案】/;
【解析】要使原不等式无解,则需满足/,得/≥2.
12. 【答案】-1</<2;
【解析】由于直线/经过A(2,1),B(-1,-2)两点,那么把A、B两点的坐标代入/,用待定系数法求出/、/的值,然后解不等式组/,即可求出解集.
13.【答案】 k≥-3;
【解析】3k-5x=-9,x=/,/ 解得k≥-3.
14. 【答案】/,/;
15.【答案】3,1;
【解析】由于本密码的解密钥匙是: 明文a,b对应的密文为a-2b,2a+b.
故当密文是1,7时,
得/, 解得/.
也就是说,密文1,7分别对应明文3,1.
16.【答案】1<a≤2.
【解析】先把a看成一个固定数,解关于x的不等式组,再由不等式组的解集研究a的取值范围.
三.解答题
17.【解析】
解:/,
由不等式①移项得:4x+x>1﹣6,
整理得:5x>﹣5,
解得:x>﹣1,…(1分)
由不等式②去括号得:3x﹣3≤x+5,
移项得:3x﹣x≤5+3,
合并得:2x≤8,
解得:x≤4,
则不等式组的解集为﹣1<x≤4.
在数轴上表示不等式组的解集如图所示,
/
18.【解析】
解:解不等式组/,
解不等式①得:x>﹣/,
解不等式②得:x≤a+4,
∵不等式组有四个整数解,
∴1≤a+4<2,
解得:﹣3≤a<﹣2.
19.【解析】
解:(1)设新建1个地上停车位需要x万元,新建1个地下停车位需y万元,
根据题意,得/, 解得:/
答:新建1个地上停车位需要0.1万元,新建1个地下停车位需0.5万元. (2)设建m个地上停车位,则建(50-m)个地下停车位,根据题意,得
12<0.1m+0.5(50-m)≤13, 解得:30≤m</ ∵m为整数, ∴m=30,31,32
∴50-m=20,19,18.
答:有三种建造方案:方案一:新建30个地上停车位和20个地下停车位;方案二:新建31个地上停车位和19个地下停车位;方案三:新建32个地上停车位和18个地下停车位.
20. 【解析】
解:(1)由图知,/≤2时是正比例函数,/≥2时是一次函数.
设/≤2时,/,把(2,6)代入/,解得/=3,
∴ 当0≤/≤2时,/.
设/≥2时,/,把(2,6),(10,3)代入/中,
得/,解得/,即/.
当/=0时,有/,/.
∴ 当2≤/≤18时,/.
(2)由于/≥4时在治疗疾病是有效的,
∴ /,解得/.
即服药后/得到/为治病的有效时间,
这段时间为/.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
