人教版九年级数学上册第二十三章旋转23.2.3关于原点对称的点的坐标学案设计含答案
文档属性
| 名称 | 人教版九年级数学上册第二十三章旋转23.2.3关于原点对称的点的坐标学案设计含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 269.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 12:17:14 | ||
图片预览

文档简介
第二十三章 旋转
23.2 中心对称
23.2.3 关于原点对称的点的坐标
学习目标
1.理解点P与点P'关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P'(-x,-y)的运用.
2.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.
学习过程
一、自主思考
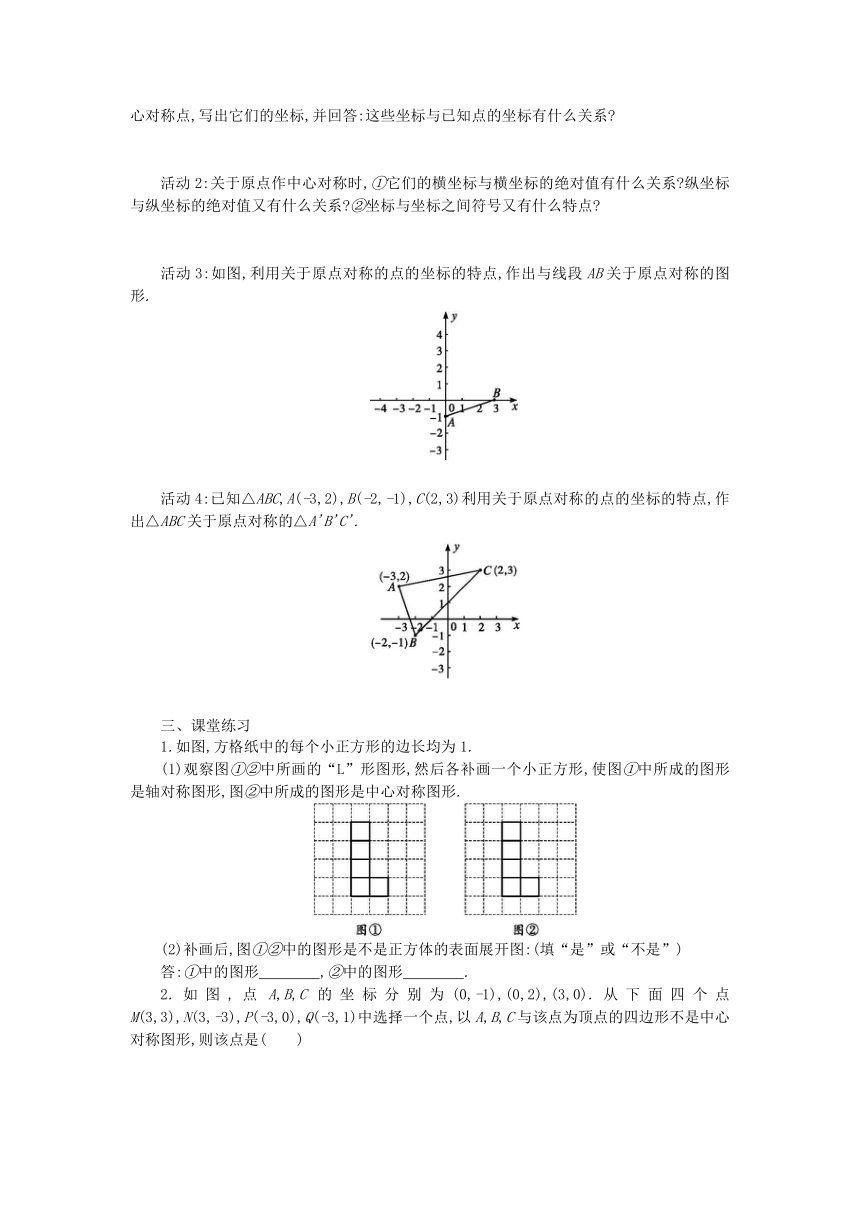
问题1:已知点A和直线l,如图,请画出点A关于l对称的点A'.
问题2:如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
问题3:如图△ABO,绕点O旋转180°,画出旋转后的图形.
二、学习新知
活动1:如图所示,在直角坐标系中,已知A(-3,1),B(-4,0),C(0,3),D(2,2),E(3,-3),F(-2,-2),作出A,B,C,D,E,F点关于原点O的中心对称点,写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
活动2:关于原点作中心对称时,①它们的横坐标与横坐标的绝对值有什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?
活动3:如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
活动4:已知△ABC,A(-3,2),B(-2,-1),C(2,3)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的△A'B'C'.
三、课堂练习
1.如图,方格纸中的每个小正方形的边长均为1.
(1)观察图①②中所画的“L”形图形,然后各补画一个小正方形,使图①中所成的图形是轴对称图形,图②中所成的图形是中心对称图形.
(2)补画后,图①②中的图形是不是正方体的表面展开图:(填“是”或“不是”)
答:①中的图形 ,②中的图形 .?
2.如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
3.下列标志既是轴对称图形又是中心对称图形的是 ( )
4.已知点P(-b,2)与点Q(3,2a)关于原点对称,则a+b的值是 .?
5.已知a<0,则点P(-a2,-a+1)关于原点的对称点P'在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
四、当堂评价,反馈深化
1.下列图形中,是轴对称图形但不是中心对称图形的是 ( )
2.已知点A的坐标为(a,b),O为坐标原点,连接OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为( )
A.(-a,b) B.(a,-b)
C.(-b,a) D.(b,-a)
3.如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是 .?
4.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P'为 .?
5.如图,请在网格中作出△ABC关于点O对称的△A1B1C1,再作出△A1B1C1绕点B1逆时针旋转90°后的△A2B1C2.
6.如图①②均为7×6的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形.(画一个即可)
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形.(画一个即可)
布置作业
1.必做题:课本第70页习题23.2第3,4题.
2.选做题:课本第70页习题23.2第10题.
参考答案
一、自主思考
问题1:图略.作法如下:过点A作直线l的垂线,垂足为M,延长AM到B使AM=BM,则B就是所求作的点.
问题2:如图所示,△ABC为所求作的图形.
问题3:图略.
二、学习新知
活动1:作法:(1)连接AO并延长AO;
(2)在射线AO上截取OA'=OA;
(3)过点A作AD'⊥x轴于点D',过点A'作A'D″⊥x轴于点D″.
∵△AD'O与△A'D″O全等,
∴AD'=A'D″,OD'=OD″,
∴A'(3,-1).
同理可得B,C,D,E,F这些点关于原点的中心对称点的坐标.
活动2:①横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.
②坐标符号相反,即设P(x,y)关于原点O的对称点为P'(-x,-y).
活动3:要作出线段AB关于原点的对称线段,只要作出点A、点B关于原点的对称点A',B'即可.因为点P(x,y)关于原点的对称点为P'(-x,-y),
所以,线段AB的两个端点A(0,-1),B(3,0)关于原点的对称点分别为A'(0,1),B(-3,0).
连接A'B',就可得到与线段AB关于原点对称的线段A'B'.
活动4:如图所示.
三、课堂练习
1.(1)如下图:
(2)图①—1(不是)或图①—2(是),图②(是).
2.C 3.A
4.2 解析:∵点P(-b,2)与点Q(3,2a)关于原点对称,∴b=3,a=-1,∴a+b=2.
5.D 解析:∵当a<0时,点P(-a2,-a+1)在第二象限,
∴则点P关于原点的对称点P'在第四象限.故选D.
四、自我检测
1.A
2.C 解析:画图可得点A1的坐标为(-b,a).
3.(5,2)
4.(-3,-6) 解析:将点P(3,n)代入y=x+3得,n=6,
∴对称点P'为(-3,-6).
5.图略.
6.解:(1)如图:
(2)如图:
23.2 中心对称
23.2.3 关于原点对称的点的坐标
学习目标
1.理解点P与点P'关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P'(-x,-y)的运用.
2.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.
学习过程
一、自主思考
问题1:已知点A和直线l,如图,请画出点A关于l对称的点A'.
问题2:如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
问题3:如图△ABO,绕点O旋转180°,画出旋转后的图形.
二、学习新知
活动1:如图所示,在直角坐标系中,已知A(-3,1),B(-4,0),C(0,3),D(2,2),E(3,-3),F(-2,-2),作出A,B,C,D,E,F点关于原点O的中心对称点,写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
活动2:关于原点作中心对称时,①它们的横坐标与横坐标的绝对值有什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?
活动3:如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
活动4:已知△ABC,A(-3,2),B(-2,-1),C(2,3)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的△A'B'C'.
三、课堂练习
1.如图,方格纸中的每个小正方形的边长均为1.
(1)观察图①②中所画的“L”形图形,然后各补画一个小正方形,使图①中所成的图形是轴对称图形,图②中所成的图形是中心对称图形.
(2)补画后,图①②中的图形是不是正方体的表面展开图:(填“是”或“不是”)
答:①中的图形 ,②中的图形 .?
2.如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
3.下列标志既是轴对称图形又是中心对称图形的是 ( )
4.已知点P(-b,2)与点Q(3,2a)关于原点对称,则a+b的值是 .?
5.已知a<0,则点P(-a2,-a+1)关于原点的对称点P'在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
四、当堂评价,反馈深化
1.下列图形中,是轴对称图形但不是中心对称图形的是 ( )
2.已知点A的坐标为(a,b),O为坐标原点,连接OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为( )
A.(-a,b) B.(a,-b)
C.(-b,a) D.(b,-a)
3.如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是 .?
4.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P'为 .?
5.如图,请在网格中作出△ABC关于点O对称的△A1B1C1,再作出△A1B1C1绕点B1逆时针旋转90°后的△A2B1C2.
6.如图①②均为7×6的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形.(画一个即可)
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形.(画一个即可)
布置作业
1.必做题:课本第70页习题23.2第3,4题.
2.选做题:课本第70页习题23.2第10题.
参考答案
一、自主思考
问题1:图略.作法如下:过点A作直线l的垂线,垂足为M,延长AM到B使AM=BM,则B就是所求作的点.
问题2:如图所示,△ABC为所求作的图形.
问题3:图略.
二、学习新知
活动1:作法:(1)连接AO并延长AO;
(2)在射线AO上截取OA'=OA;
(3)过点A作AD'⊥x轴于点D',过点A'作A'D″⊥x轴于点D″.
∵△AD'O与△A'D″O全等,
∴AD'=A'D″,OD'=OD″,
∴A'(3,-1).
同理可得B,C,D,E,F这些点关于原点的中心对称点的坐标.
活动2:①横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.
②坐标符号相反,即设P(x,y)关于原点O的对称点为P'(-x,-y).
活动3:要作出线段AB关于原点的对称线段,只要作出点A、点B关于原点的对称点A',B'即可.因为点P(x,y)关于原点的对称点为P'(-x,-y),
所以,线段AB的两个端点A(0,-1),B(3,0)关于原点的对称点分别为A'(0,1),B(-3,0).
连接A'B',就可得到与线段AB关于原点对称的线段A'B'.
活动4:如图所示.
三、课堂练习
1.(1)如下图:
(2)图①—1(不是)或图①—2(是),图②(是).
2.C 3.A
4.2 解析:∵点P(-b,2)与点Q(3,2a)关于原点对称,∴b=3,a=-1,∴a+b=2.
5.D 解析:∵当a<0时,点P(-a2,-a+1)在第二象限,
∴则点P关于原点的对称点P'在第四象限.故选D.
四、自我检测
1.A
2.C 解析:画图可得点A1的坐标为(-b,a).
3.(5,2)
4.(-3,-6) 解析:将点P(3,n)代入y=x+3得,n=6,
∴对称点P'为(-3,-6).
5.图略.
6.解:(1)如图:
(2)如图:
同课章节目录
